-
摘要: 介绍了一种基于内接正八面体和Snyder投影的近似等积格网构建方法。先构建与球面面积相等的正八面体,将正八面体的面作为初始剖分面,然后采用四元三角剖分方法将初始剖分面分割成层次嵌套的三角格网,利用Snyder等积投影将正八面体面上的层次格网投影至球面,用大圆弧代替Snyder投影弧,构建近似等积的全球离散格网系统。在分析Snyder投影弧和大圆弧差异的基础上,依次计算各层次格网的面积、长度、角度值;根据计算结果分析了不同层次近似等积格网面积、长度、角度变形规律及空间分布特征。结果表明,随着剖分层次的增加,格网面积误差呈减小的趋势;剖分层次为10时,99.8%的格网面积偏差在-10%~10%之间,面积变形较大的格网均位于由正八面体面的中心到三个顶点的连线附近;格网长度、角度最大值与最小值的比均呈收敛的趋势,分别收敛至1.73和3.03。Abstract: In this article, a method for constructing an approximate equal area grid based on the octahedron and Snyder projection is introduced. An octahedron that has equal surface area to a sphere is built; each face of this octahedron is considered as initial subdivision surface. Then, each initial surface is subdivided into hierarchical triangles using a quaternary triangular subdivision scheme, which are projected onto the surface of sphere using Snyder projection. The arc projecting polyhedron triangles onto the spherical surface is modified by using great circle line instead of Snyder projection arc. A new approximate equal area global discrete grid system is constructed. Based on the analysis of difference between the great circle arc and Snyder projection arc, the values of area, edge length, and angle of different subdivision level grids are calculated according to corresponding spherical calculation equation. Based the calculation results, different levels of approximately equidistant grid areas, lengths, angles, and spatial distributions of the deformation are analyzed. Results indicate that with increasing osubdivision levels, 1) the difference in grid areas is very little; area errors of 99.8% of the grids are between -10% and 10%. The girds with heavy area distortion are near the lines between the middle point and three vertexes of octahedron surface, when subdivision level is equal to 10; 2) the ratio increments of the maximum and minimum values of grid areas and edge length show a trend toward convergence, converging to 1.73 and 3.03 respectively.
-
倾斜摄影测量技术已广泛应用于逼真地形景观建模等领域,其基本特点是从多角度影像自动获取密集点云数据,通过简化处理生成不规则三角网格表面模型(triangulated irregalar network,TIN),并自动映射纹理[1, 2]。实际上,受多视影像联合平差精度和密集匹配生成的点云精度的限制,以及点云简化的不足,会导致生成的三角形网格模型表面粗糙,连续区域表面法向量存在噪声,从而造成不一致性。这种不一致性导致对应于同一地物表面的三角面片被投影到不同影像上;同时,由于相机畸变、光照、地物反射特性等原因,不同影像间存在几何和辐射上的差异,最终纹理映射后的结果呈碎片化状态,三维场景真实感不强、不直观。当前主流的倾斜影像处理软件如Street Factory等也都存在类似的问题。
纹理映射碎片化问题的解决方法主要有渐入渐出法[3]、光照连续性重建[4, 5]法以及应用较广泛的多波段融合法[6-9]等。这些方法都是从影像出发,通过匀光或色彩融合等处理,使其在灰度上趋于一致,虽然在一定程度上可以使碎片之间的纹理过渡更加平滑,但计算量大,算法要求高,容易出现模糊和重影现象,并且依然难以消除碎片化的影响。
纹理映射碎片化的根本原因是模型表面上相邻的三角面片由于几何不一致被投影到不同影像上。现有方法只是在影像层面对纹理进行修复,并没有从根本上解决模型表面的几何不一致性问题。针对此,本文提出一种局部区域表面一致性约束的纹理映射方法,采用一致性约束的区域生长方法和分块区域整体的纹理优选方法,解决上述纹理碎片化的问题。
1 算法基本原理
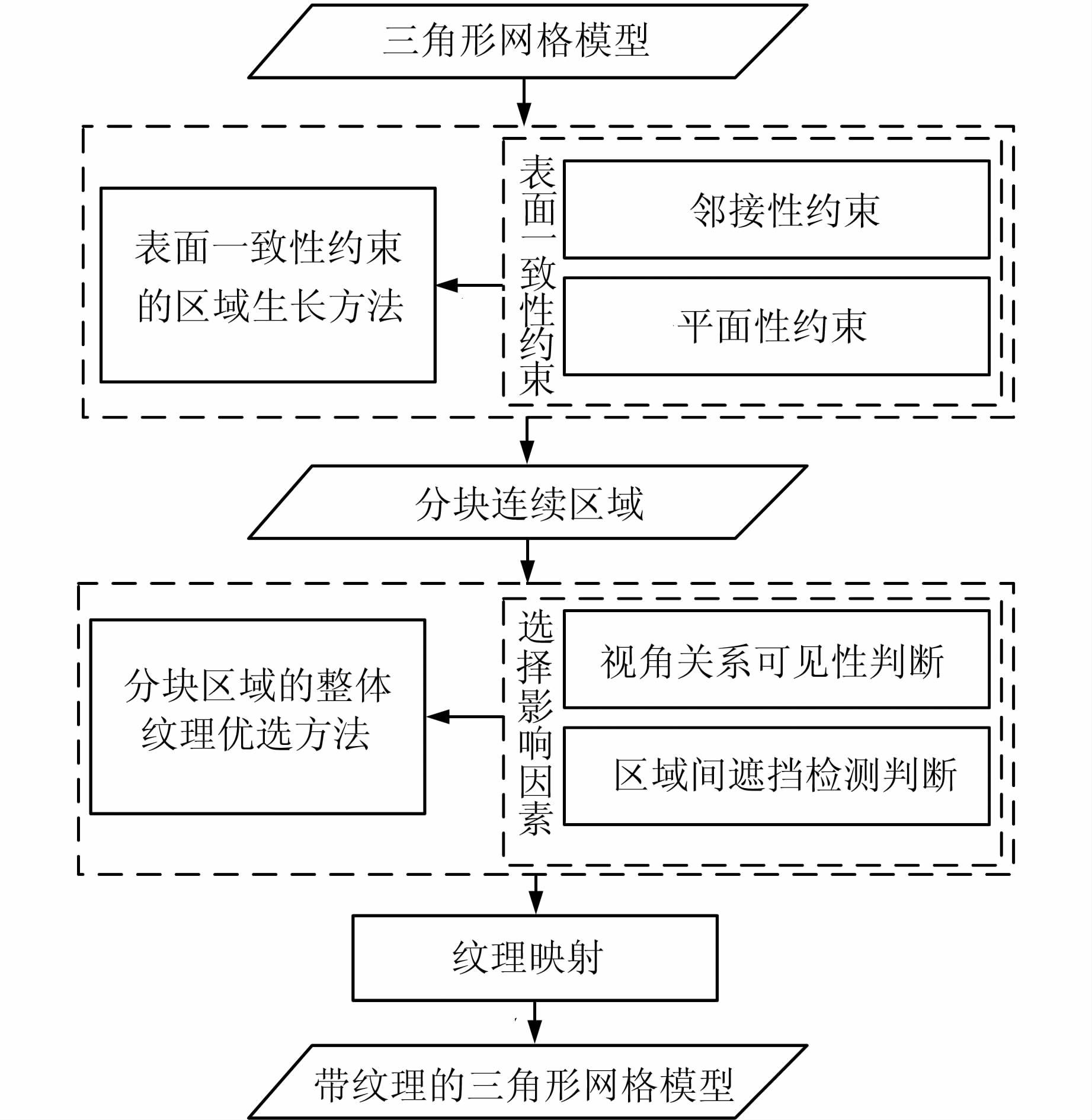
局部区域表面一致性约束的纹理映射方法流程如图 1所示。记三角形网格模型为M[9],构成M的带有法向量的三角形记作有向三角面片t,则M的连续表面S={t1,t2,…,tm},S∈R3。首先,在表面一致性约束的前提下,以有向三角面片t为基元,采用表面一致性约束的区域生长算法将S分割为多个分块连续的区域R1,R2,…,Rn,RiS(1 ≤ i ≤ n),且分割结果应在最大程度上满足人们对建筑物几何表面划分的认知,即连续、光滑建筑物有且仅有一个表面与之对应。为了保证局部区域内纹理映射的连续性,需要根据区域整体的纹理优选方法,从覆盖区域Ri的多张不同角度的影像中,选择一张最佳影像为Ri提供纹理。最后根据投影矩阵计算Ri上的点在影像上的投影,得到纹理,完成纹理映射。
1.1 表面一致性约束的区域生长方法
纹理映射的碎片化是由于三角形网格模型M表面的几何不一致性引起的。产生不一致性的原因是影像平差精度和密集匹配的点云精度的限制以及构网过程中的简化算法不够完善,导致连续区域表面的法向量存在异常噪声。如图 2所示,Γ为建筑物真实的表面,n为其法向量,t1、t2为M表面两个相邻的三角面片,n1、n2为其法向量。
单独来看,t1、t2与Γ之间的夹角θ1、θ2均在噪声容忍范围内,但t1与t2之间的夹角θ=θ1+θ2却超过了噪声容忍范围,形成噪声。表面一致性约束不是剔除噪声点,而是通过约束,使噪声点可以与邻近点形成一个具有一致性的区域,即该区域是连续的,并且区域上任何一点在同一张影像上具有相同的可见性。因此,表面一致性约束包括邻接性约束和平面性约束两方面。
1.1.1 邻接性约束
邻接性约束,即三角面片在空间上是相邻的,能保证区域的连续性。邻接性约束可通过采用树状的索引结构(KD-Tree、R-Tree[10-12]等),进行半径搜索或K邻近搜索来实现。但是由于三角形网格模型密度的不均匀性,进行半径搜索时难以设置合适的阈值以保证每次搜索的有效性,故本文中采用K邻近搜索方法。
K邻近搜索方法实现区域生长的关键是K的取值。平坦的模型表面K一般取较大值,可以加速计算;而对于房屋角点、植被等复杂表面,由于存在多个平面,K一般由大到小渐进取值,这样既能保证分割出每一个平面,又能保证计算效率。本文中,首先令K取一个较大的值(K=20)进行搜索,判断搜索到的点是否满足平面性约束,若不满足则说明是复杂表面,此时令K值减半继续搜索,以此类推。这样既可以保证计算速度,又可以保证区域生长结果在多个平面交界处的准确性。
1.1.2 平面性约束
实际中,许多建筑物的表面由连续曲面构成,但是曲面上的不同点在同一张影像上不具备相同的可见性(不考虑其他面的遮挡)。如图 3(a)所示,Γ 为建筑物真实的表面,I1、I2、I3是不同角度的拍摄的影像,p0 ~p4为Γ上的点,p0 ~p2为I1的可视范围,p1 ~p3为I2的可视范围,p2 ~p4为I3的可视范围,可见Γ上的点不可能全部投影到同一张影像上,因此需要对其进行平面性约束,用多个平面逼近曲面,如图 3(b)所示。
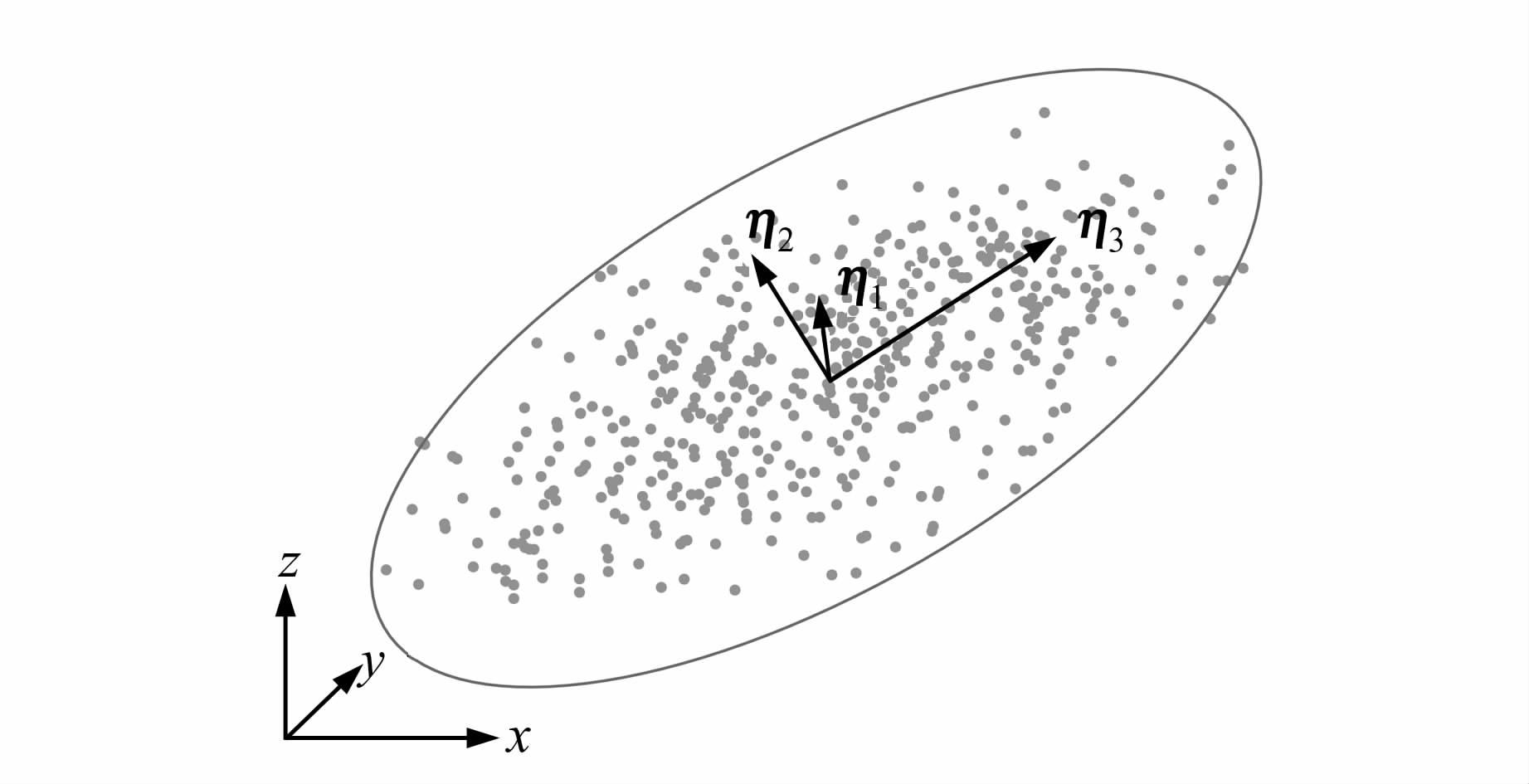
设有向点集P(P∈R3),P的平面度可以通过其协方差矩阵的主成分分析来判断[13],对协方差矩阵进行奇异值分解(singular value decomposition,SVD)后得到特征值σ1 <σ2 <σ3,η1、η2、η3为对应的特征向量,如图 4所示。特征值及其对应的特征向量代表了P在三维空间中的分布情况,σ1越小P越接近平面,极限情况为σ1=0。因此,平面性约束可记为:

(1) 式中,σ2 /σ1 >ξ1可保证点集P近似为平面,而σ3 /σ2 <ξ2则能避免产生过于狭长的条带。本文中采用这种方法作为平面性约束,令ξ1=45,ξ2=15,既有效约束了平面的形状,也较好地包容了噪声点。
若P满足上述约束,则可拟合出平面并记n0为拟合平面的法向量,近似于图 2中建筑物表面Γ的实际法向量n,x为平面上的点。设P中一点pi的法向量ni与n0之间的夹角记为θ(ni,n0),需满足:

(2) 由前面对法向量噪声的分析可知,式(2)避免了法向量噪声对平面的影响。式(1)和式(2)共同构成平面性约束,在区域生长时可将连续的曲面及平滑的过渡地带分割为多个平面逼近。
1.1.3 顾及约束的区域生长方法
区域生长以有向三角面片t为基元,采用迭代的策略由种子点向外生长。为了方便计算,将t的几何重心点及其法向量构成有向点p,则全部有向三角面片t的集合S即对应于有向点集P。区域生长需要解决的三个关键问题为种子点的选取,包含进区域的准则以及生长停止的条件。
以P为数据源创建Kd-Tree,记生长出的区域为R,其边界为B,符号⊕(p)表示添加点p,Θ(p)表示从集合中删除点p,并且添加一个点后都需要将它从KD-Tree中删除,以避免重复计算。首先,从P中任选一点p0作为种子点,R⊕(p0)、B⊕(p0),标记p0为起始点;以B中第j个标记为起始点的点pBj为中心进行K=20的邻近搜索,若搜索到的点{pnew}与R一起满足平面性约束式(1)、式(2),则R⊕{pnew}、B⊕{pnew},标记{pnew}为起始点,并且BΘ(pBj);若不满足平面性约束式(1)、式(2),则K值减半进行搜索,若直到K=1时{pnew}与R一起仍不满足约束条件,则标记pBj为终止点;然后重新令K=20,搜索B中第j+1个标记为起始点的点;逐此迭代,直到B中所有点均标记为终止点,或K邻近搜到的结果为空为止,则停止生长。最后得到的R即为所求的连续区域,它拟合的平面的法向量可视为R的法向量nR,nR是后面选择投影影像时的关键因素。若KD-Tree不为空,则以剩下的点中任意一点为某个区域生长结束后的种子点,进入下一个区域的生长。
1.2 分块连续区域的整体纹理优选方法
倾斜摄影测量具有多角度、多时相的特点,因此区域R会被多张影像I1,I2,…,Im同时覆盖。R与影像间的方位关系不同,在影像上产生投影畸变的程度也不同;同时由于区域间的遮挡关系,R在不同影像上的可见情况不同。因此,需要选择一张最佳的影像来为R提供整体的纹理。
1.2.1 视角关系判断及区域间遮挡检测
倾斜摄影测量中不同角度影像在空间中的方位是固定的,以5头相机为例, 影像范围覆盖同一区域的相机A、B、C、D、E分布如图 5(a)所示。定义ρ为区域与影像之间的视角关系权重,它与两个角度有关:① 区域R的法向量nR与每张影像投影反方向nI之间所成的夹角,记为α;② 以R的中心为起点,连接影像中心,得到向量l,记l与nR之间的夹角为β,如图 5(b)所示,A1、A2、A3为不同时刻相似A在空中的位置。β越小,则R在影像上的投影越靠近影像中心。
则ρ的确定方式如下:

(3) 当ρ大于0时,区域R在影像上可见(不考虑遮挡和超出影像范围)。为了保证投影的质量,令:

(4) 以区域R为整体进行遮挡检测,若R中总三角面片个数为s,被遮挡和超出影像范围的个数为k,记η为R在影像上的遮挡比率:

(5) 1.2.2 最佳影像优选方法
区域R整体的纹理优选方法需同时考虑视角关系ρ和遮挡比率η。首先找出所有ρ大于0对应的影像,并从中选取ηmin所对应的影像作为R的最佳投影影像Ibest。若ηmin大于0,则说明R在Ibest上不完全可见,此时需要将不可见的部分分割出来作为一个单独的区域R′,再以同样的方法为R′选择最佳投影影像。最后,从每一块区域对应的最佳投影影像中提取纹理,进行纹理映射。
2 实验分析
为了验证上述方法的有效性,本文采用SWDC-5的倾斜摄影影像数据来进行实验。整个测区共被15张影像所覆盖,相机A、B、C、D、E分别各有3张影像,影像覆盖区域内包括道路、建筑物(弧形/非弧形)、操场、植被等多种地物。对这些影像进行多视影像联合匹配后生成点云,再利用构网算法得到三角形网格模型,作为纹理映射的模型基础。
对比实验将三角形格网模型M中的有向三角面片t逐个按照§1.2中的方法选择最佳投影影像,然后再将投影到同一张影像上的相邻三角面片连接为一个区域R。这种逐个三角形纹理映射的方法与本文方法之间的区别在于是否进行了一致性约束的区域生长。图 6(a)为逐个三角形纹理映射的结果;图 6(b)为本文方法进行一致性约束的区域生长后的分割结果。将三角形个数小于一定阈值的区域视为碎片,可看出图 6(a)中碎片化现象严重,而图 6(b)中区域连续一致,地面和立面、立面和屋顶被很好地分割开,并且弧形的建筑物表面被分割为6个连续的近似平面,以保证能够正确地选择投影影像。实验中对一个具有60 000个三角面片的三角形网格模型分别在两种方法下形成的连续区域R进行统计分析,其结果见表 1。可看出,本文方法可将碎片化程度减小到逐个三角形纹理映射方法的5%,而这些碎片主要分布在植被不规则的表面、建筑物内凹形成的坑洞表面以及细小地物的表面等处。
表 1 区域生长前后碎片化程度对比Table 1. Comparison of Fragmentation Degrees of the One-by-one Approach and Our Approach方法 总连通区域个数 三角形个数<10的连通区域个数 三角形个数<5的连通区域个数 三角形个数=1的连通区域个数 平均包含的三角形个数 逐个三角形映射方法 11 755 10 766 9 640 5 748 5.1 一致性约束的区域生长方法 909 541 457 216 66.0 图 7为纹理映射后的对比结果。图 7(a)为Street Factory建模并进行纹理映射的结果。从图 7(a)可看出,虽然Street Factory对纹理进行了匀光处理,但仍存在纹理碎片化的现象;图 7(b)、7(c)分别为同一个三角形网格模型在逐个三角面片纹理映射和一致性约束纹理映射的结果,显然逐个三角面片的纹理映射结果受噪声影响较大,尤其是在水面和植被处的纹理碎片化现象严重;而一致性约束纹理映射结果则有显著改善。
3 结 语
本文提出了一种针对三角形网格模型的局部区域表面一致性约束的纹理映射方法,并使用真实数据与Street Factory等商业软件进行了对比实验。表面一致性约束可大大减小三角形网格模型表面噪声(尤其是法向量噪声)的影响,顾及这种约束的区域生长方法能够将三角形网格模型良好地分割为多个连续的区域,最终为每一个区域选择最优的投影影像提供纹理。这种化零为整的思想对消除纹理碎片化现象具有显著效果。进一步的研究将针对更加复杂的建筑物场景的真实感表达进行,以期消除不同建筑物间的纹理接缝,增强场景的真实感。
-
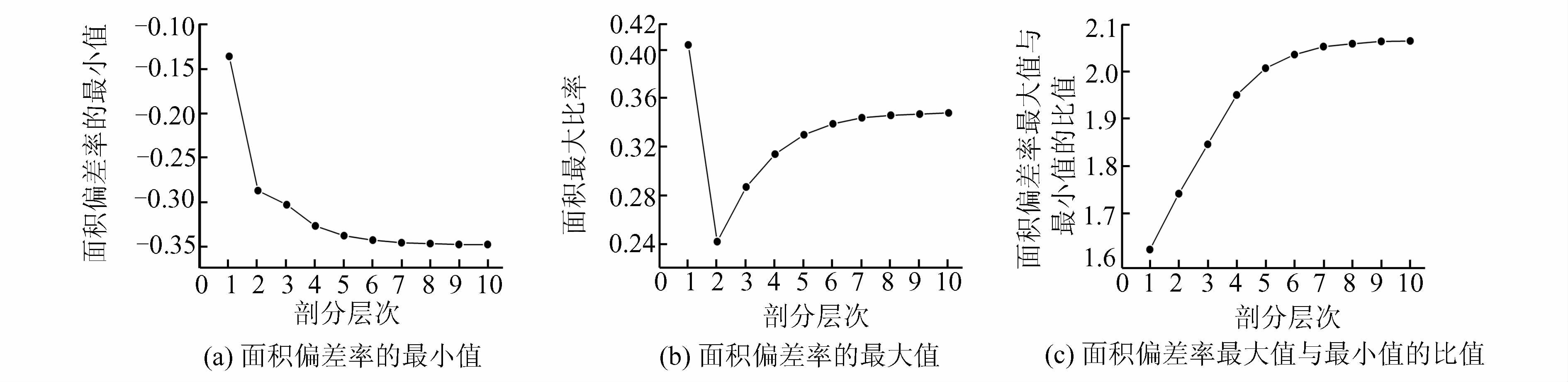
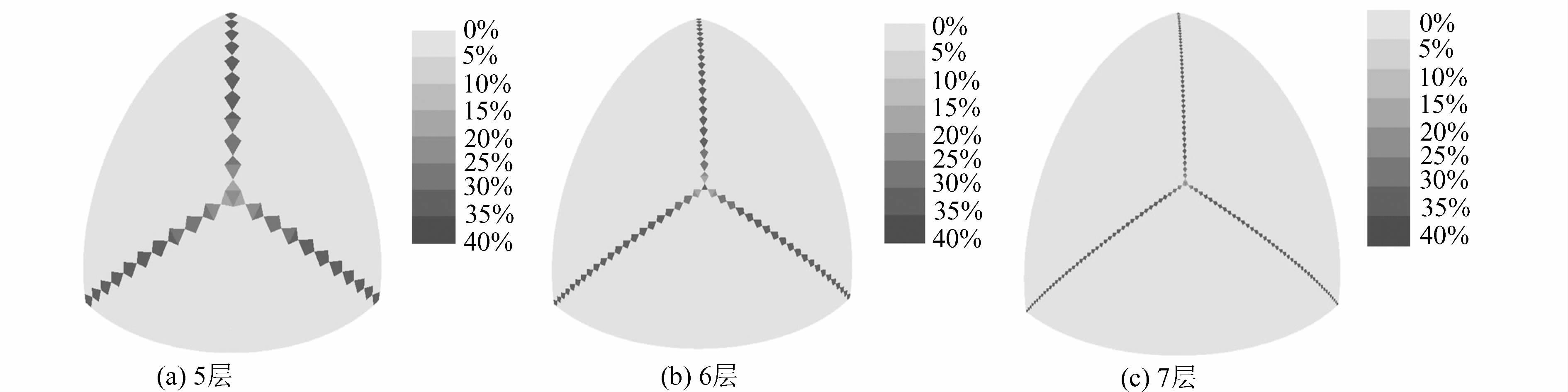
表 1 不同面积变形格网的统计情况
Table 1 Statistics of Grid Numbers with Different Area Distortion
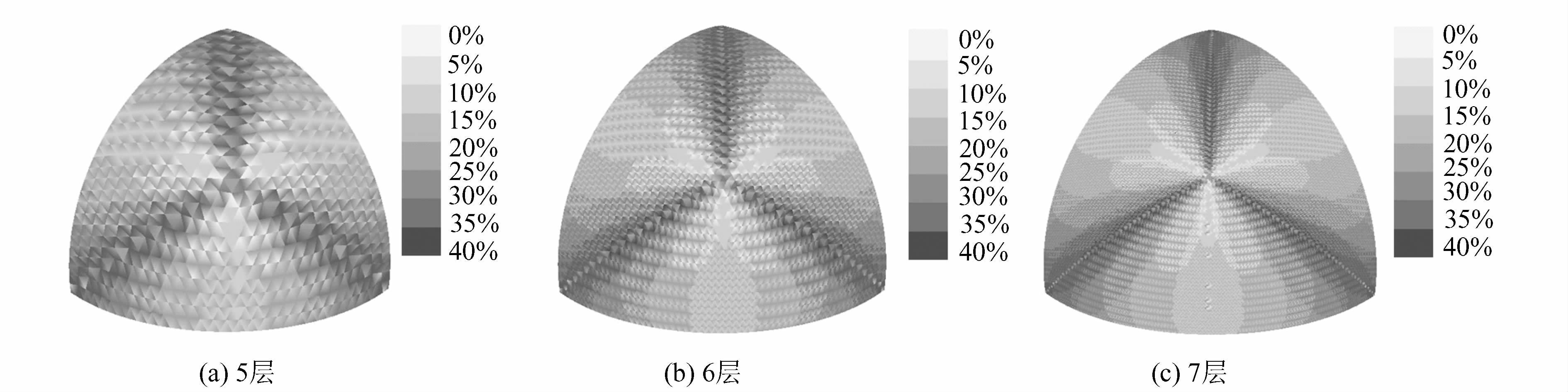
层次 面积偏差率的最小值 40%~-30% -30%~-20% -20%~-10% -10%~0 0~10% 10%~20% 20%~30% 30%~40% 面积偏差率的最大值 面积偏差率最大值与最小值的比 1 -0.135 0 0 3 0 0 0 0 1 0.404 1.623 2 -0.287 0 4 0 0 9 0 3 0 0.242 1.742 3 -0.303 3 3 3 21 27 0 7 0 0.287 1.847 4 -0.327 10 6 0 105 120 3 6 6 0.314 1.952 5 -0.338 24 6 3 453 507 0 10 21 0.330 2.009 6 -0.343 55 9 0 1 941 2 028 3 6 54 0.339 2.038 7 -0.346 120 6 3 7 971 8 157 0 10 117 0.344 2.055 8 -0.347 247 9 0 32 343 32 682 3 6 246 0.346 2.061 9 -0.348 504 6 3 130 164 130 956 0 10 501 0.347 2.066 10 -0.348 1 015 9 0 522 837 523 692 3 6 1 014 0.348 2.067 表 2 格网长度变形的统计情况
Table 2 Statistics of Grid Length Distortions
层次 长度偏差率的最小值 -30%~-20% -20%~-10% -10%~0 0~10% 10%~20% 20%~30% 长度偏差率的最大值 长度偏差率最大值与最小值的比 1 -0.18 0 6 0 6 0 0 0.10 1.33 2 -0.20 6 12 0 12 18 0 0.12 1.41 3 -0.23 18 48 0 66 60 0 0.18 1.53 4 -0.24 60 198 0 210 276 24 0.22 1.59 5 -0.24 228 774 24 924 930 192 0.24 1.64 6 -0.25 906 3 108 84 3 642 3 732 816 0.26 1.67 7 -0.25 3 570 12 402 414 14 712 14 586 3 468 0.27 1.69 8 -0.25 14 208 49 694 1 636 58 686 58 032 14 352 0.28 1.71 9 -0.25 56 754 198 816 6 576 234 510 231 552 58 224 0.29 1.72 10 -0.25 226 920 795 198 26 460 937 980 924 246 234 924 0.29 1.72 表 3 格网最大、最小变形角度的统计情况
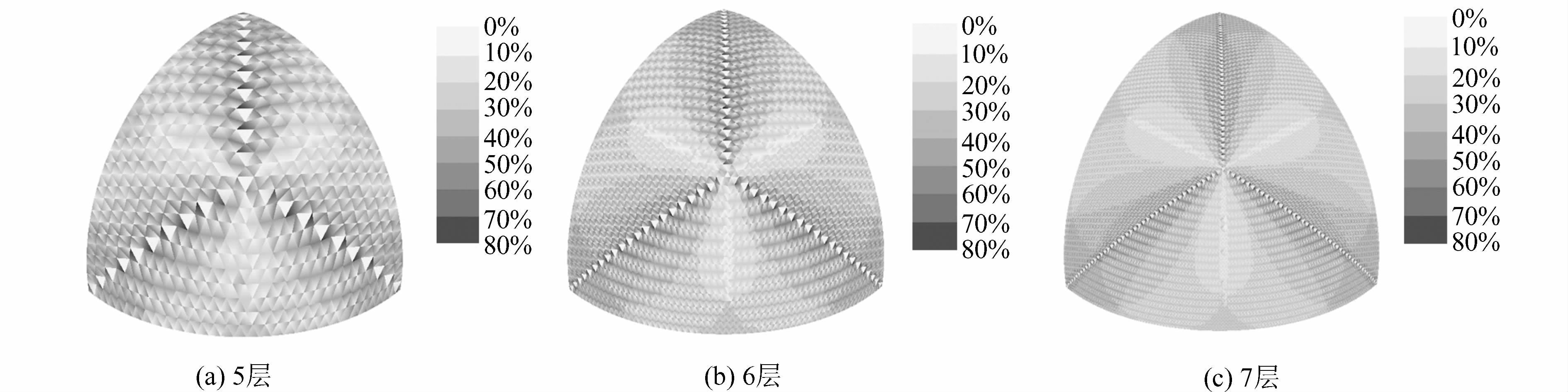
Table 3 Statistics of Max and Min Angle Distortions of Grids
层次 1 2 3 4 5 6 7 8 9 10 角度偏差率的最小值 -0.09 -0.25 -0.33 -0.38 -0.40 -0.41 -0.41 -0.42 -0.42 -0.42 角度偏差率的最大值 0.52 0.52 0.57 0.63 0.67 0.70 0.72 0.74 0.74 0.75 角度偏差率最大值与最小值的比 1.68 2.03 2.34 2.61 2.78 2.88 2.94 2.98 3.01 3.03 表 4 格网角度变形的统计情况
Table 4 Statistics of Grid Angle Distortions
层次 -50%~-40% -40%~-30% -30%~-20% -20%~-10% -10%~0 0~10% 10%~20% 20%~30% 30%~40% 40%~50% 50%~60% 60%~70% 70%~80% 1 0 0 0 0 6 0 3 0 0 0 3 0 0 2 0 0 15 0 0 12 18 0 0 0 3 0 0 3 0 12 42 12 9 54 30 24 3 0 6 0 0 4 0 84 144 27 30 201 165 84 18 0 9 6 0 5 0 360 540 129 69 828 615 420 81 0 12 18 0 6 126 1 392 2 034 549 213 3 324 2 529 1 644 414 0 15 42 6 7 708 5 394 8 159 2 140 693 13 277 10 018 6 726 1 887 24 27 54 45 8 3 270 21 217 32 447 8 631 2 573 52 917 40 378 27 007 7 841 72 48 93 114 9 14 010 84 150 129 738 34 311 9 724 211 451 161 595 108 468 32 313 162 87 171 252 10 58 050 335 010 518 238 137 400 37 638 845 418 646 929 434 646 131 046 330 171 333 519 -
[1] Geogory M J, Kimerling A J, White D,et al. A Comparison of Intercell Metrics on Discrete Global Grid System[J]. Computer, Environment and Urban Systems, 2008, 32:188-203 doi: 10.1016/j.compenvurbsys.2007.11.003
[2] Keister A R, Sahr K. Planar and Spherical Hierarchical, Multi-resolution Cellular Automata[J]. Computer, Environment and Urban Systems, 2008, 32:204-213 doi: 10.1016/j.compenvurbsys.2008.03.001
[3] Daniela R. Uniform and Refinable Grids on Elliptic Domains and on Some Surfaces of Revolution[J]. Applied Mathematics and Computation, 2011, 217:7812-7817 doi: 10.1016/j.amc.2011.02.095
[4] Daniela R, Gerlind P. Uniform Spherical Grids via Equal Area Projection from the Cube to the Sphere[J]. Journal of Computational and Applied Mathematics, 2011, 236:1033-1041 doi: 10.1016/j.cam.2011.07.009
[5] Sahr K, White D, Kimerling A. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2):121-134 doi: 10.1559/152304003100011090
[6] Sahr K. Location Coding on Icosahedral Aperture 3 Hexagon Discrete Global Grids[J]. Computer, Environment and Urban Systems, 2008, 32:174-187 doi: 10.1016/j.compenvurbsys.2007.11.005
[7] Titz S, Kuhlbrodt T, Feudel U. Grid Geometry Effects on Convection in Ocean Climate Models:A Conceptual Study[J]. Ocean Modeling, 2004, 7:165-181 doi: 10.1016/j.ocemod.2003.08.001
[8] Teanby N A. An Icosahedron-based Method for Even Binning of Globally Distributed Remote Sensing Data[J]. Computer & Geosciences, 2006, 32:1442-1450 http://cn.bing.com/academic/profile?id=2071000950&encoded=0&v=paper_preview&mkt=zh-cn
[9] 孙文彬,周长江. 一种近似等积球面菱形格网的构建方法[J]. 武汉大学学报·信息科学版, 2016, 41(8):1040-1045 http://ch.whu.edu.cn/CN/abstract/abstract5504.shtml Sun Wenbin, Zhou Changjiang. A Method of Constructing Approximate Equal-area Diamond Grid[J]. Geomatics and Information Science of Wuhan University, 2016,41(8):1040-1045 http://ch.whu.edu.cn/CN/abstract/abstract5504.shtml
[10] Kimerling A J,Sahr K, White D, et al. Comparing Geometrical Properties of Global Grids[J]. Cartography and Geographic Information Science, 1999, 26(4):271-288 doi: 10.1559/152304099782294186
[11] White D, Kimmerling A J, Sahr K, et al. Comparing Area and Shape Distortion on Polyhedral Based Recursive Tessellations of the Sphere[J]. International Journal of Geographical Information Science, 1998, 12(8):808-827 https://www.researchgate.net/publication/220649496_Comparing_Area_and_Shape_Distortion_on_Polyhedral-Based_Recursive_Partitions_of_the_Sphere
[12] Goodchild M F. Geographical Grid Models for Environmental Monitoring and Analysis Across the Globe(Panel Session)[C]. GIS/LIS'94 Conference, Phoenix Arizona, USA, 1994
[13] Kimerling A J. Predicting Data Loss and Duplication when Resampling from Equal-angle Grids[J]. Cartography and Geographic Information Science, 2002, 29(2):111-126 doi: 10.1559/152304002782053297
[14] Gregory M J, Kimerling A J, White D, et al. A Comparison of Intercell Metrics on Discrete Global Grid Systems[J]. Computers, Environment and Urban Systems, 2008, 32:188-203 doi: 10.1016/j.compenvurbsys.2007.11.003
[15] Ming T, Zhuang D F, Yuan W. The Study on Geometrical Distortion of Triangular Partitions in Discrete Global Grids[C]. 2008 International Workshop on Education Technology and Training & 2008 International Workshop on Geoscience and Remote Sensing, Sanya, China,2008
[16] Ming T, Zhuang D F. The Geometrical Distortion of Discrete Global Grid in Multi-resolution Expression[C]. 2009 International Conference on Environmental Science and Information Application Technology, Beijing, China, 2009
[17] 赵学胜,孙文彬,陈军. 基于QTM的全球离散格网变形分布及收敛分析[J]. 中国矿业大学学报, 2005, 34(4):438-442 http://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD200504007.htm Zhao Xuesheng, Sun Wenbin, Chen Jun. Distortion Distribution and Convergent Analysis of the Global Discrete Grid Based on QTM[J]. Journal of China University of Mining & Technology, 2005, 34(4):438-442 http://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD200504007.htm
[18] 贲进, 童晓冲, 张永生,等. 球面等积六边形离散网格的生成算法及变形分析[J]. 地理与地理信息科学, 2006, 22(1):7-11 http://www.cnki.com.cn/Article/CJFDTOTAL-DLGT200601001.htm Ben Jin, Tong Xiaochong. Zhang Yongsheng, et al. A Generation Algorithm of Spherical Equal-area Hexagonal Discrete Grid and Analysis of Its Deformation[J]. Geography and Geo-information Science, 2006, 22(1):7-11 http://www.cnki.com.cn/Article/CJFDTOTAL-DLGT200601001.htm
[19] 张胜茂, 吴健平,周科松. 基于正多面体的球面三角剖分与分析[J]. 计算机工程与应用, 2008, 44(9):16-19 http://www.cnki.com.cn/Article/CJFDTOTAL-JSGG200809005.htm Zhang Shengmao, Wu Jianping, Zhou Kesong. Spherical Triangle Subdivision and Analysis Based on Polyhedron[J]. Computer Engineering and Application, 2008, 44(9):16-19 http://www.cnki.com.cn/Article/CJFDTOTAL-JSGG200809005.htm
[20] 白建军,孙文彬,赵学胜. 基于QTM的WGS-84椭球面层次剖分及其特点分析[J]. 测绘学报, 2011, 40(2):243-248 http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201102021.htm Bai Jianjun, Sun Wenbin, Zhao Xuesheng. Character Analysis and Hierarchical Partition of WGS-84 Ellipsoidal Facet Based on QTM[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2):243-248 http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201102021.htm
[21] Snyder J P. An Equal-area Map Projection for Polyhedral Globes[J]. Cartographica, 1992, 29(1):10-21 doi: 10.3138/27H7-8K88-4882-1752
[22] 侯妙乐,赵学胜,陈军. 球面四元三角网局部拓扑不变量的计算与应用[J].武汉大学学报·信息科学版, 2010, 35(12):1504-1507 http://www.cnki.com.cn/Article/CJFDTOTAL-WHCH201012029.htm Hou Miaole, Zhao Xuesheng, Chen Jun.Computation of Local Topologic Invariant in Spherical Surface Quaternary Triangular Mesh and Its Application[J]. Geomatics and Information Science of Wuhan University, 2010, 35(12):1504-1507 http://www.cnki.com.cn/Article/CJFDTOTAL-WHCH201012029.htm
[23] 白建军,赵学胜,陈军. 基于椭球面三角格网的数字高程建模[J]. 武汉大学学报·信息科学版, 2005, 30(5):384-387 http://ch.whu.edu.cn/CN/abstract/abstract2177.shtml Bai Jianjun, Zhao Xuesheng, Chen Jun. Digital Elevation Modeling Based on Hierarchical Subdivision of the Triangular Meshed on Ellipsoidal Surface[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5):384-387 http://ch.whu.edu.cn/CN/abstract/abstract2177.shtml
[24] 侯妙乐,赵学胜,陈军. 球面四元三角网的三拓扑数计算[J]. 武汉大学学报·信息科学版, 2008, 33(1):61-63, 104 http://ch.whu.edu.cn/CN/abstract/abstract1482.shtml Hou Miaole, Zhao Xuesheng, Chen Jun. Computation of Three Topological Number on Spherical Quaternary Triangular Mesh[J]. Geomatics and Information Science of Wuhan University, 2008, 33(1):61-63, 104 http://ch.whu.edu.cn/CN/abstract/abstract1482.shtml
[25] 侯妙乐,邢华侨,赵学胜,等. 球面四元三角网的复杂拓扑关系计算[J].武汉大学学报·信息科学版, 2012, 37(4):469-471, 481 http://ch.whu.edu.cn/CN/abstract/abstract172.shtml Hou Miaole, Xing Huaqiao, Zhao Xuesheng,et al. Computing of Complicated Topological Relation in Spherical Surface Quaternary Triangular Mesh[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4):469-471, 481 http://ch.whu.edu.cn/CN/abstract/abstract172.shtml
[26] 赵学胜,范德芹,王娇娇,等. 退化四叉树格网的全球多分辨率DEM无缝表达[J]. 测绘学报, 2012, 41(6):918-925 http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201206023.htm Zhao Xuesheng, Fan Deqin, Wang Jiaojiao,et al. Seamless Expression of the Global Multi-resolution DEMs Based on Degenerate Quadtree Grids[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6):918-925 http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201206023.htm
-
期刊类型引用(10)
1. 刘飞鹏. 消费型无人机在河道精细化三维构建中的应用. 测绘与空间地理信息. 2024(03): 29-31+35 .  百度学术
百度学术
2. 周友华,邢小平. Multigen Creator几何建模中的纹理优化. 电脑编程技巧与维护. 2021(01): 145-146+171 .  百度学术
百度学术
3. 朱庆,张琳琳,胡翰,翁其强,丁雨淋,李赟,张叶廷. 精细建筑物碎片化纹理优化的二维装箱方法. 西南交通大学学报. 2021(02): 306-313 .  百度学术
百度学术
4. 王梦威,马秀丽. 基于中介媒介的交互式纹理映射. 电子测量技术. 2020(12): 115-120 .  百度学术
百度学术
5. 叶震,许强,刘谦,董秀军,王晓晨,宁浩. 无人机倾斜摄影测量在边坡岩体结构面调查中的应用. 武汉大学学报(信息科学版). 2020(11): 1739-1746 .  百度学术
百度学术
6. 马立华,郑永虎,丛晓明,冷旻航. 无人机倾斜摄影测量三维仿真飞行在龙羊峡水电站高陡边坡数据获取中的应用. 青海科技. 2020(06): 72-76 .  百度学术
百度学术
7. 乃古色拉,张云生,张明磊,邹峥嵘. 基于图割算法的倾斜影像纹理映射优化方法. 测绘与空间地理信息. 2019(03): 145-147 .  百度学术
百度学术
8. 朱庆,翁其强,胡翰,王峰,王伟玺,杨卫军,张鹏程. 基于帧缓存的多角度影像精细纹理映射方法. 西南交通大学学报. 2019(02): 269-277 .  百度学术
百度学术
9. 黄明,贾嘉楠,李闪磊,张建广,龚建辉. 多像位姿估计的全景纹理映射算法. 武汉大学学报(信息科学版). 2019(11): 1622-1632 .  百度学术
百度学术
10. 梁玉斌,崔铁军. 倾斜摄影测量的研究进展. 天津师范大学学报(自然科学版). 2017(05): 1-6 .  百度学术
百度学术
其他类型引用(11)





 下载:
下载: