Undifferenced and Uncombined PPP Ambiguity Resolution Combined with GPS/GLONASS Triple-Frequency Observations
-
摘要:
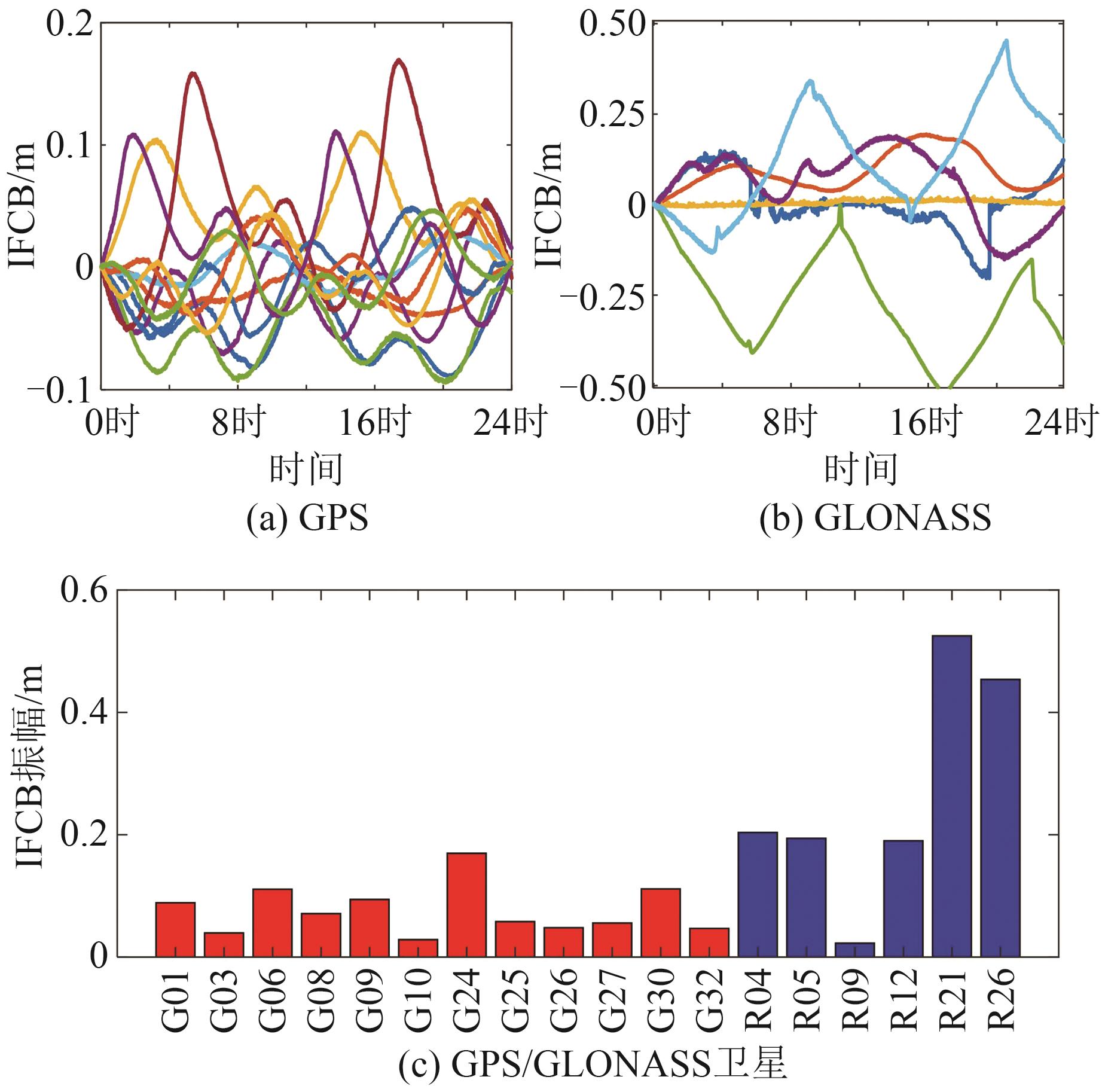
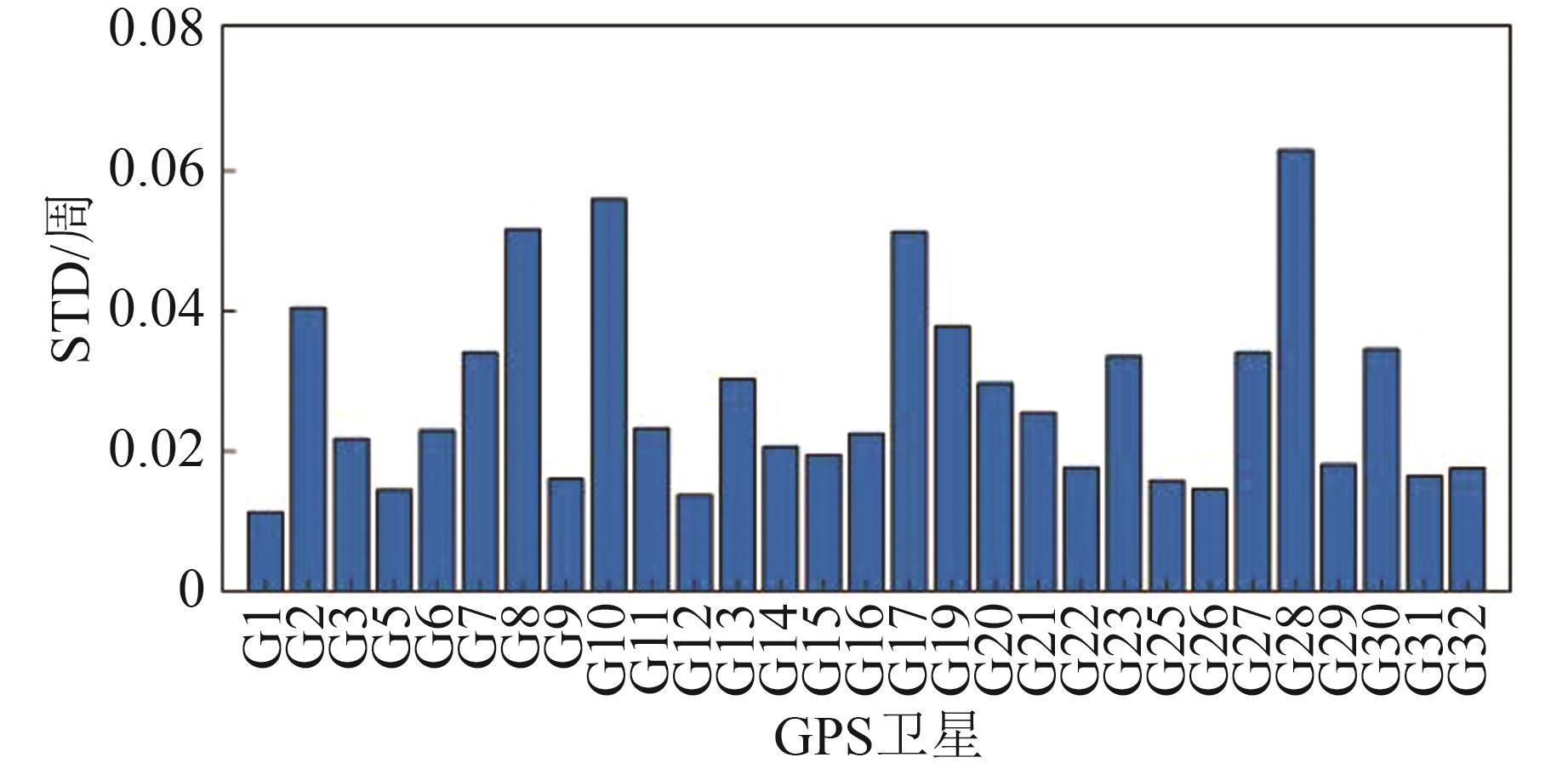
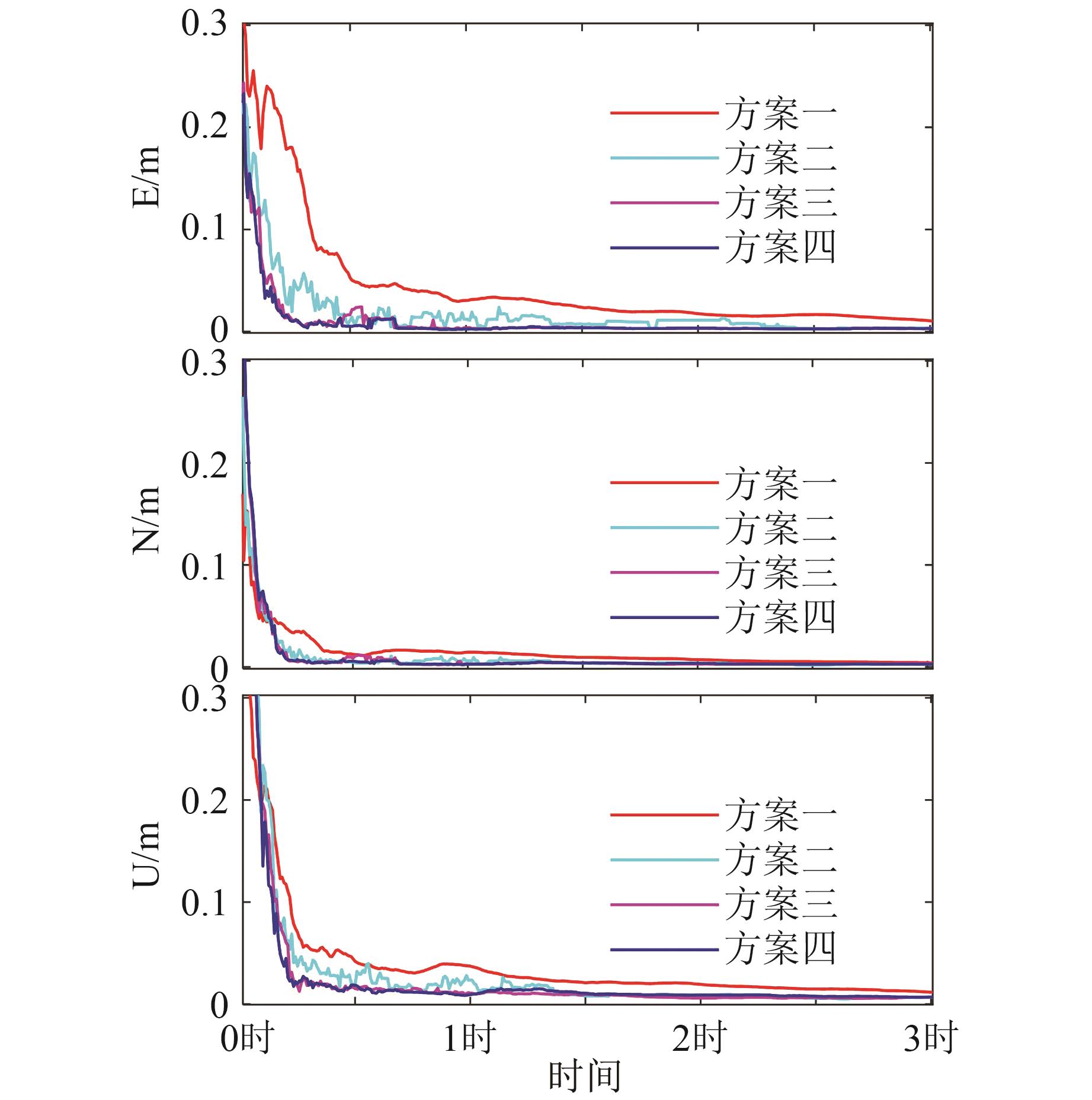
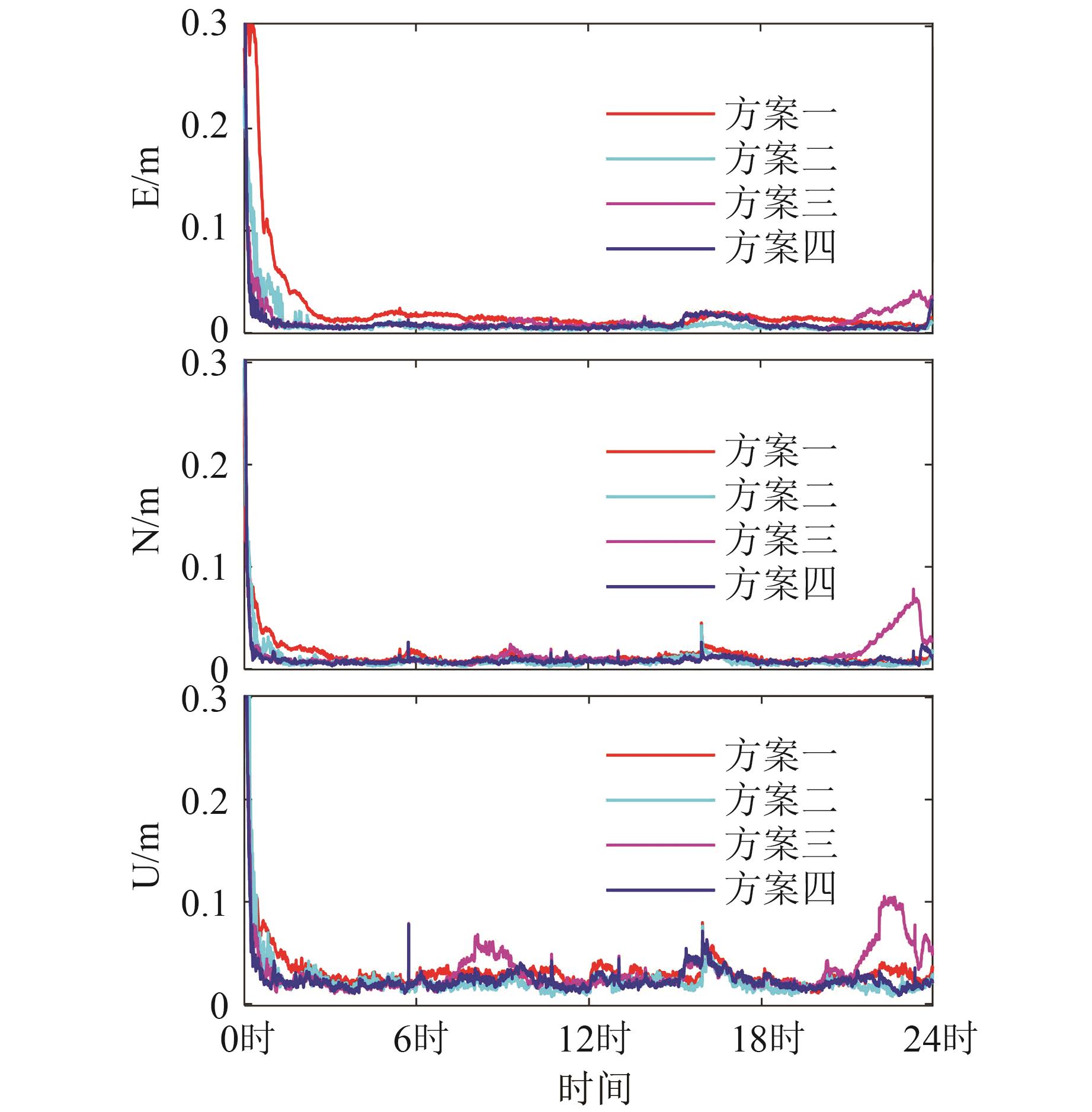
俄罗斯全球导航卫星系统(global navigation satellite system, GLONASS)目前有4颗GLONASS-M+卫星和两颗GLONASS-K1卫星支持在第3个频点传输码分多址(code division multiple access,CDMA)信号,使得研究GLONASS三频精密单点定位(precise point positioning, PPP)成为可能。为顺应多频多系统发展趋势,研究了联合GPS和GLONASS三频观测值的非差非组合PPP模糊度固定(ambiguity resolution, AR)模型与方法,推导了顾及频率间钟偏差(inter-frequency clock bias, IFCB)影响的GPS+GLONASS三频非差非组合PPP模型,给出了服务端三频非差未校验相位延迟(uncalibrated phase delay, UPD)估计方法和用户端三频PPP-AR策略。但限于当前GLONASS三频观测数据数量及其分布,实验中组合GPS和GLONASS观测值进行三频非组合PPP-AR,但只固定GPS三频模糊度,而GLONASS模糊度保持其浮点形式。利用全球分布的300余个多模全球卫星导航系统实验跟踪网(multi-GNSS(global navigation satellite system) experiment, MGEX)测站估计IFCB和UPD改正产品,14个MGEX测站用于用户端PPP-AR性能评估,结果表明:组合GPS和GLONASS观测值进行三频非组合PPP-AR,但只固定GPS三频模糊度实现了快速收敛,此外相对于GPS单系统三频PPP-AR,静态解在东、北、天和三维方向上定位精度提升幅度分别达到80.7%、60.0%、61.0%和63.8%,仿动态解提升分别达到41.9%、14.5%、11.6%和16.3%。若忽略GLONASS三频IFCB误差,组合GPS和GLONASS三频PPP-AR在收敛序列出现较大幅度的波动,定位性能甚至不及GPS单系统固定解。组合GPS和GLONASS观测值进行三频非组合PPP-AR可实现模糊度快速固定,静态和仿动态实验模糊度平均首次固定时间分别为12.3、12.9 min,相较于GPS单系统提升显著,其中仿动态实验提升率达53.8%。此外,相对于组合GPS三频观测值和GLONASS双频观测值方案,添加GLONASS三频观测值后,仿动态偏差序列稳定性得到小幅改善。
-
关键词:
- GPS+GLONASS /
- 非差非组合PPP /
- 三频AR /
- FDMA+CDMA观测值
Abstract:ObjectivesCurrently, two global navigation satellite system (GLONASS)-K1 and four GLONASS-M+ satellites transmit code division multiple access (CDMA) signals on the third frequency in addition to the traditional frequency division multiple access (FDMA) signals on the first two frequencies, making it possible for GLONASS joint use of FDMA and CDMA signals for precise point positioning (PPP). To follow with the trend of multi-frequency and multi-system, GPS+GLONASS triple-frequency uncombined PPP ambiguity resolution (AR) model is investigated.
MethodsFirst, a GPS+GLONASS triple-frequency uncombined PPP model considering the inter-frequency clock bias (IFCB) of GPS and GLONASS systems is presented. Then we present the triple-frequency uncalibrated phase delay (UPD) estimation method and PPP-AR algorithm. However, limited to the number of GLONASS triple-frequency observations and its distribution, we combine GPS and GLONASS triple-frequency observations for PPP-AR, but only fix GPS triple-frequency ambiguities, while GLONASS ambiguity maintains its floating-point form. The IFCB and UPD products are estimated by more than 300 multi-GNSS experiment (MGEX) stations distributed around the world, and another 14 MGEX stations are used to evaluate PPP-AR performance.
ResultsExperimental results demonstrate that the best positioning performance has been achieved by our algorithm. Compared with GPS triple-frequency PPP-AR, the positioning accuracies of the static experiments in the east, north, up and 3D directions are improved by 80.7%, 60.0%, 61.0% and 63.8% respectively, and that of the simulated dynamic experiments are improved by 41.9%, 14.5%, 11.6% and 16.3%. However, if GLONASS IFCB errors are ignored, the stability of the convergence series of the combined triple-frequency PPP-AR will be harmed, causing the positioning performance even inferior to GPS single system. Moreover, our algorithm achieves rapid ambiguity resolutions. The average time to first fix time of static and simulated dynamic experiments of our model is about 12.3 and 12.9 min respectively, which is significantly improved compared with GPS, in which the improvement of the simulated dynamic experiment is 53.8%. Besides, compared with the scheme of combining GPS triple-frequency observations and GLONASS dual-frequency observations, after integrating GLONASS CDMA observations, the stability of the positioning time series of the simulated dynamic experiments is effectively improved, and the root mean square value of positioning errors in each direction can be reduced.
ConclusionsThese results demonstrate that the best positioning performance can be achieved by the proposed GPS+GLONASS triple-frequency PPP-AR. Moreover, GLONASS IFCB errors must be carefully investigated and calibrated beforehand. However, limited by the number of GLONASS CDMA datasets and other factors, it is difficult to perform GLONASS triple-frequency PPP-AR with FDMA and CDMA signals currently. In the future work, we will focus on the investigation of GLONASS triple-frequency PPP-AR.
-
大地测量是监测地壳运动与地壳变形,开展地震危险性判定及预测预报研究的重要手段。自1966年邢台地震以来,经过半个多世纪的努力,中国业已建立了具有一定监测能力的地形变观测网络[1-3],并在认识地壳运动及研究同震形变等方面取得了较重要的科研成果[4-10],但在震前变形与地震关系研究方面,主要以震例研究为主,在研究思路和研究方法上未有明显突破。
2008年5月12日汶川Ms 8.0地震发生在青藏高原东部巴颜喀拉地块与华南地块交界的NE向龙门山断裂带上,该断裂带包括前山断裂(frontrange fault,FF)、中央断裂(central fault,CF)和后山断裂(backrange fault,BF)(图 1)。地表破裂带分别沿中央断裂中、北段和前山断裂中段展布,震源破裂起始于映秀镇以西,朝北东呈单侧破裂扩展至青川附近,共形成了约240 km的地表断裂带。断层破裂运动以逆冲和右旋走滑分量为主,同震垂直位移为4~6 m,右旋水平位移为3~5 m[11-12]。沿该断裂带附近有多个地倾斜观测点和跨断层水准观测场地,临震前没有观测到显著的前兆信息[13],因此,在汶川地震后的多次研讨会上,不少专家对大地测量观测技术及观测意义提出质疑。
依据弹性回跳理论和构造形变特点,在20世纪60年代国际上首次提出利用监测断层预滑移进行地震预报的思路,并成为各国地壳形变观测网络规划及地震预测的重要依据。许多学者认为,大地震前在发震断层附近应该能监测到预滑移或显著变形异常,如指数型加速变化。然而,自21世纪以来,国际上一些震例研究发现,即使在发震断层附近布设相对密集的形变观测网,进行倾斜、应变和跨断层水准测量等,临震前仍可能难以观测到显著的变形异常[14-18]。
形变前兆和地震之间的关系看似不同寻常,但它有自身的规律和原因[19]。本文以震中区和外围场地形变观测数据为基础,重点研究汶川地震前不同构造部位、不同时间尺度地壳变形过程特征,通过相关分析探究震前变形与大区域地震活动之间的联系。
1 汶川地震孕育发生背景
汶川地震是2001年昆仑山Ms 8.1地震后中国大陆7级地震平静6年之久,在2008年新疆于田Ms 7.3地震打破平静后发生的一次灾难性地震。这次地震夺去了69 227人的生命,使17 927人下落不明,受灾人口4 625万,直接经济损失8 451亿元,是新中国成立以来发生在中国境内受灾面积最大、损失最重的一次地震。
汶川地震发生的构造及动力背景已有许多学者进行了研究[20-21],图 1为汶川地震孕育发生的动力背景。由图 1可以看出,由于印度板块对欧亚板块的强烈推挤以及青藏高原的强烈隆升作用,使得青藏地块产生E向和SE向的水平挤出运动。巴颜喀拉地块属于青藏地块的次级块体之一,它在E向和SE向的水平挤出运动中,受到华南地块的阻挡而产生纵向变形,使得该块体的前端地壳增厚。同时,该块体20~25 km深度上存在的低速带可成为上地壳与中-下地壳相对运动的“解耦”带,该低速带沿SE向延伸,终止于龙门山断裂带之下,使得低速带终止端附近上地壳的SE向水平运动被迫转换为龙门山断裂带的逆冲运动,从而促进汶川地震的发生。
中国大陆受到欧亚板块、印度洋板块和太平洋板块的联合作用,与地震活动相关的应力场往往具有较广泛的区域。已有研究发现,中国东南沿海的大地震以圆形地震构造为特征,圆形地震段与中国大陆的大地震互补[22],与汶川地震相关的动力因素可扩展到环太平洋地震带[23]。2001年昆仑山地震后,Ms 5.5及以上地震主要分布在青藏高原东部、华东南地区和台湾地区,并形成一个近于SE向的地震活动空区,如图 2所示。
地震空区主要指地震活动的间隙区,可分为两类:一类是地震带上大地震震源区分布的空段,另一类是缺少中小地震的区域[24]。汶川地震发生在龙门山断裂一百多年来7级地震活动的空段上和2000年以来4级地震活动的空区内[25]。由于不同区域地震活动背景不同,空区的划分没有明确的界定[26],本文给出的地震空区指Ms 5.5地震活动的内边界。
汶川地震发生前,中国地壳运动观测网络(crustal movement observation network of China,CMONOC)中全球卫星导航系统(global navigation satellite system,GNSS)个别站点的观测结果,也为揭示汶川地震的孕育发生过程提供了重要信息,本文选取的相关站点分布如图 2所示。
2 数据和基本分析方法
2.1 地倾斜数据
获取并研究震中区的变形特征是认识地震孕育发生过程的一个重要途径。因此,在一些地震多发区域都曾建有地形变观测场地或台站,以期捕捉到震前发震断层的预滑移信息[1-3]。为监测龙门山断裂带断层活动,在20世纪70年代沿该断裂带开始流动跨断层水准观测,2002年在汶川等地又开展了地倾斜观测。
汶川台是距震中最近的形变观测台站,位于龙门山断裂带的后山断裂上,台站位置见图 1。本文收集整理了汶川台自2002年10月开始正常观测至汶川地震前的地倾斜数据,时间跨度约6年。该台采用石英摆倾斜仪,在洞深25 m、覆盖层40 m、年温差低于0.3°的山洞内进行观测,2个独立的钵体分别进行EW向和NS向观测,钵体固定在同一大理石墩上,光杆距均为5.0 m,采取光照相记录,人工读取整点值。对观测以来EW向与NS向倾斜进行潮汐分析,发现潮汐因子变化较为稳定,其中NS向和EW向潮汐因子误差分别为0.019和0.094。
2.2 GNSS站间基线
自1999年以来,CMONOC有24个GNSS站开始连续观测并记录数据,在地震空区周围有少量GNSS站,包括泸州、广州、厦门、德令哈、下关和昆明等站点。广州-泸州基线和厦门-泸州基线靠近椭圆长轴方向,德令哈-泸州基线连接昆仑山Ms 8.1和汶川Ms 8.0地震的震中区,下关-泸州和昆明-泸州基线靠近椭圆短轴方向。
应用GNSS站坐标每天解算结果,计算距震中较近的泸州站至周边GNSS站间的大地线长度作为基线长度。将第一天的基线长度置为零,得到基线相对变化量。为滤除基线中高频信息的影响,本文采取了6阶DB小波进行拟合,给出了相对稳定的趋势变化。
2.3 Benioff蠕变
应用Kanamori能量-震级经验公式[27],以1个月为窗长逐月滑动,计算研究区域任意时段Ms 5.5及以上地震释放的Benioff蠕变,它能够反映区域地震能释放水平[28-29]。本文计算使用中国地震台网中心地震目录(见https://data.earthquake.cn/czdzml/index.html),该目录对于Ms 5.5及以上地震较为完备[25]。
2.4 相关分析方法
选择最初变化趋势较好的时间段作为基准,对Benioff蠕变数据和GNSS基线数据分别建立线性模型并进行滤波,得到两个近于平稳、但包括异常的残差序列。选择最简单的相关模型,以GNSS基线残差为因变量,Benioff蠕变残差为自变量,建立回归模型,获取两个残差序列之间的回归系数及拟合误差。如模型拟合残差位于2倍均方差内的点占比高于95%,即认为符合正态分布,模型检验有效。
3 数据分析与计算结果
3.1 汶川台地倾斜特征分析
汶川台NS向倾斜变化具有较平稳的年变特点,年变化幅度约为260 ms,未有显著的异常特征。图 3为汶川台EW向地倾斜变化,其中A、B为速率变化转折点。由图 3可以看出,EW向倾斜序列具有明显的非线性,可分为3个线性段,分别为2002-10—2004-12(A点)、2005-01—2007-01(B点)及2007-02—2008-05(汶川地震前)。每个阶段地倾斜变化都具有相对平行的上、下包络线,取上、下包络线的中间为阶段趋势线,趋势线的斜率表示倾斜变化速率,3个阶段的变化速率分别约为-230 ms/a、-130 ms/a和-60 ms/a。对各个阶段进行线性滤波得到相应的残差,获得整个序列的期望值为0.0 ms,均方根误差为75.2 ms,残差序列中97.5%的点分布在2倍均方根误差内,满足正态分布检验条件。地倾斜序列的3个阶段的划分与同处龙门山断裂带后山断裂上映秀场地重力阶段性变化特点接近[30]。
3.2 GNSS基线分析
按照GNSS站点分布及地震活动区域特点,本文选取靠近汶川地震震中区的泸州站与周边站点间的5条基线,基线长度变化曲线如图 4所示,其中C、D为速率变化转折点。
具体分析如下:
1)泸州GNSS站是距离汶川地震震中最近的一个基准站,距震中约200 km。德令哈-泸州基线靠近空区椭圆长轴方向,且连接了昆仑山Ms 8.1和汶川Ms 8.0地震的震中区。由图 4(a)可以看出,由于受印度板块和欧亚板块的共同作用,巴颜喀拉地块受到NE向挤压,川滇地区呈现东向逃逸,德令哈-泸州基线变化以拉张为主。2008年3月中旬开始,该基线出现快速反向变化,直到汶川地震发生,持续时间近2个月,最大异常幅度约8 mm。类似的现象也出现在昆仑山地震前,2001年7月底出现显著反向加速变化,持续时间3个月,最大异常幅度约5 mm,地震发生在加速停滞、回复过程中,地震后回复原有趋势。下关-泸州和昆明-泸州基线是靠近空区椭圆短轴方向的两条基线。由图 4(b)可以看出,自2006年初开始,下关-泸州基线拉伸速率减缓,呈现持续的负异常,直到汶川地震前,异常幅度达30 mm。由图 4(c)可以看出,昆明-泸州基线在汶川地震前出现小幅度扰动,无显著趋势变化异常。
2)厦门GNSS站位于中国东南沿海地区,距离中国台湾岛较近。台湾岛位于菲律宾和琉球两条俯冲构造带的交接部位,在台湾岛的南、北两端以NW向转换断层与之相接,由于菲律宾海板块与欧亚大陆板块和太平洋板块的相互碰撞聚合作用,在台湾岛形成了以中央山脉为主要代表的挤压逆冲构造形变带,发育着大量NE或近NS走向的叠瓦状逆冲或逆掩断层,构造变形和地震活动都非常强烈,碰撞挤压作用还影响到台湾海峡和东南沿海等地[31-32]。厦门-泸州基线近似分布在空区椭圆的长轴方向,由图 4(d)可以看出,由于受菲律宾板块NW向挤压及地震活动影响,其主要表现压性变化。台湾地区地震活动分布呈现丛集性,研究时间段内,Ms 5.5及以上地震集中分布在2002年中、2003年底至2005年中,2006年底至2007年中,每个时间段都有Ms 7.0以上地震发生。在地震丛集发生间隙,厦门-泸州基线呈现较快速的压缩变化,表明该基线所受挤压作用增强。由于台湾周边地震活动较有节律,汶川地震前该基线并没有显著的挤压变化异常。
3)由图 4(e)可以看出,广州-泸州基线在汶川地震前变化较为显著。2001年初至2004年底(C点),该基线以约0.8 mm/a的缩短速率变化,具有较好的年变化形态;2005年初至2007年中(D点),该基线以约8 mm/a的速率快速缩短,最大累积压缩幅度约20 mm,这在华南地区较为少见;2007年中之后,该基线开始回复,直到汶川地震发生。
3.3 区域地震的Benioff蠕变分析
图 5为2001—2008年中国大陆Ms 5.5及以上地震震级-时间图和相应的Benioff蠕变释放曲线,其中E、F为转折点。由图 5可以看出,昆仑山Ms 8.1地震后1~3年,地震能量释放速率较为稳定;2004年9月开始(E点),释放速率显著减小,直到2007年6月(F点),地震应变释放一直处于亏损状态;2007年6月至汶川地震前,蠕变继续亏损。汶川地震后,蠕变速率基本回复到E点之前的水平。
大地震前Benioff蠕变亏损现象在以往也出现过。2001年昆仑山Ms 8.1地震前,中国大陆最近发生的一个大地震是1951年西藏当雄Ms 8.0地震,距其600 km。在西藏当雄地震后的最初几年,Benioff蠕变释放较有规律,后变得较为平静,在其后的每次Ms 7.0地震前都可监测到不同时间尺度的蠕变释放亏损现象。
4 讨论
4.1 震中区变形特征
对汶川台地倾斜速率变化阶段性特征研究表明,2008年汶川震前3年倾斜持续减速,且临震前0.5年未检测到显著的指数加速变化,这一特点与通常对地震前兆的理解有很大不同。其主要原因在于,震前变形与震间变形、同震形变和震后变形不同,在地震未发生前,并没有或不存在一个实质上的位错源。随着应变的不断积累,发震断层还可能出现高度闭锁现象,使得临震前震中附近变形速率越来越小,异常越来越少。这是地震预测面临的一个问题,也为地震预测研究提供了新的思路。
从中长期预测来看,地震前3~5年震中区可能观测到变形速率减小现象,反映了区域应变快速积累的开始。因此,可将其作为中长期大地震危险区判定及阶段性判别的一个主要的依据[33]。
临震前发震断层附近观测不到显著变形加速异常,可能反映了临震前震中附近变形的一个常态特征,因此,变形速率最小的地区或断层有可能是未来发震区域或发震断层。在孕震区,如有较密集的形变观测台网,有可能观测到一些加速变形异常,根据其异常特征可给出相应的震级范围、震中距离范围或震中方位估计,利用异常所在断层寻找与其斜交的断层作为未来发震断层[34-35],这对于地震短期预测是很有意义的。本文笔者及其团队开展了一些预测实验,对2021年漾濞Ms 6.4地震、2021年泸县Ms 6.0地震和2022年德令哈Ms 6.0地震进行了一定程度的短期预测。
4.2 广州-泸州GNSS基线缩短与Benioff蠕变变化亏损相关性
对比图 5(b)和图 4(e)可以发现,两者异常的开始时间(E点和C点)和结束时间(F点和D点)较为接近,震前特征均为负异常,异常幅度均较为显著,相关系数为0.89。为进一步分析其相关性变化,应用线性模型对两者进行模型分析。
1)对广州-泸州基线日值数据通过取月均值转化为月采样,即每月1个值。2001年11月为第一个月,i=1;汶川地震当月,i=79;2008年12月为最后一个月,i=86。
2)以2004年12月之前的基线及Benioff蠕变为基础数据构建线性模型,并进行滤波,分别得到残差,计算式为:
式中,
、 分别表示基线变化相对值和残差值,单位为mm; 分别为标准化的Benioff蠕变及线性滤波残差值,量级为108。 3)对于i=1, 2…78,通过相关分析方法得到:
式中,
表示以Benioff蠕变对广州-泸州GNSS基线拟合的误差,其均方根误差为1.70 mm,以96.2%的概率服从正态分布。 图 6为广州-泸州基线缩短与Benioff蠕变相关分析。由图 6可以看出,在汶川地震前,即i=1,2…78,GNSS基线缩短与Benioff蠕变之间存在较强的相关性,通过相关分析获得的广州-泸州基线拟合残差为一个平稳过程。
对比图 5(b)与图 4(e)还可以发现,汶川地震前广州-泸州GNSS基线缩短与Benioff蠕变亏损异常正相关,而汶川地震后变为负相关。通过对震后数据相关分析,得到回归系数为-3.0。回归系数由6.0变化到-3.0,可以简单理解为汶川地震释放能量的50%转化为当地的地应变。对于i=79, 80…86,则有:
借助Benioff蠕变对广州-泸州基线异常,分别进行震前、震后相关分析,全部时序过程残差
均值为0.0 mm,拟合均方根误差为1.62 mm,有96.55%点分布在2倍拟合误差范围内,模型检验成立,广州-泸州GNSS基线异常变化与Benioff蠕变相关。由于在最初的计算中未滤除基线中的年周期,所有残差中也存在明显的年周期。图 6中也给出了滤除拟合残差年周期后的结果,平均值为0.0 mm,均方根误差为0.72 mm,服从正态分布。 广州-泸州基线与Benioff蠕变具有较高的相关性,主要是与Benioff蠕变表示的意义有关。地震释放的能量E同样可以用断层错动位移来描述[36]:
式中,
和 分别表示走滑分量 和倾滑分量ΔUd释放的能量; 表示剪切模量;L为断层长度。式(6)可简化为: 式中,
。 由式(7)可知,每次地震的Benioff蠕变正比于地震断层位错量,反映了地震释放能量的平方根。当区域地震活动按照一定的速率释放时,难以积累更大规模的应变能;当地震活动开始出现平静时,区域大规模的应变积累也将开始。由图 4(c)中广州-泸州基线加速缩短的开始时刻(C点)和结束时刻(D点)可知,加速缩短异常持续时间约2.5年,按照加速变形时间与地震震级间的关系公式[37],得到相应地震震级估计为7.9级。与汶川地震的震级较为吻合,表明震前该基线加速缩短过程与汶川地震的应变积累具有一定的相关性。
比较图 4中泸州GNSS站至周边站间基线变化特点也可以发现,汶川地震前不同方向基线变化特征是有差别的。沿靠近空区长轴方向的广州-泸州基线在2005年初开始加速缩短,沿靠近短轴方向的下关-泸州基线在2006年初拉张速率开始减缓,而其他方向基线长期异常特征不明显;连接昆仑山地震和汶川地震震中区的德令哈-泸州基线短期特征较明显,在震中附近临震前变形较弱的情况下,该基线短期变化对8级地震具有较好的反映能力。
不同方向基线变化特点的差异性,可能反映了大震前不同构造部位对汶川地震应变积累具有不同的作用,及不同站间基线对外围大震具有不同的响应。
4.3 远场大地震发生后应力松弛效应对汶川地震孕育过程影响
自1900年以来,青藏高原和巴颜喀拉地块的强震活动表现出多期活动和区域迁移特征。20世纪早期Ms 7.0以上强地震活动的主体地区在青藏高原北部边界构造带,中期转移到高原南部喜马拉雅板块边界构造带和南部地块,最近十多年来则在巴颜喀拉地块及周缘边界断裂上活动。青藏高原的块体活动和地震活动与澳大利亚-印度板块对亚洲大陆的推挤作用相关,因此,青藏高原和巴颜喀拉地块的强震活动与澳大利亚-印度板块边界的苏门答腊强震活动相对应[38]。
从地理位置上看,昆仑山地震、苏门答腊地震和汶川地震近似呈直角三角形分布,汶川地震震中位于该三角形的顶点附近(图 7)。从大震发震间隔上看,苏门答腊地震与昆仑山地震间隔1 138天,汶川地震与苏门答腊地震间隔1 233天,时间间隔较为接近。
2001年昆仑山Ms 8.1地震和2004年苏门答腊Ms 8.9地震对汶川地震的孕育过程具有不同的作用。由图 5可知,昆仑山Ms 8.1地震后至2004年中,中强地震活动较为正常,地震活动蠕变释放较有规律,同期,汶川台EW向倾斜(图 3)及各方向基线变化速率较为稳定(图 4)。因此,昆仑山Ms 8.1地震对汶川地震的孕育发生过程影响较弱。
2004年苏门答腊Ms 8.9地震对川滇地区的地震活动和变形影响较大。苏门答腊地震破裂长度约1 200~1 500 km,破裂宽度约150~200 km,距震中3 000 km以外的测站还可观测到1~2 cm的同震位移[39]。苏门答腊地震后,汶川台EW向倾斜速率即快速减小(图 3中A点);广州-泸州基线(图 4(e))也开始出现显著的速率增大,至汶川地震前该基线最大异常幅度达20 mm;下关-泸州基线(图 4(b))速率显著减小出现在震后1年,至汶川地震前异常幅度约30 mm。不难理解,这些变形异常与苏门答腊地震引起的远场应力松弛效应和汶川地震的应变积累有一定关联。苏门答腊地震后,青藏高原地区Ms 5.5及以上地震活动出现了持续时间达3年之久的平静,也有利于大规模地震应变的积累。
由此可见,苏门答腊Ms 8.9地震的发生对川滇地区应力应变场及地震活动具有显著的影响,从而加速了汶川地震的孕育发生过程。
5 结语
通过对汶川地震震中区汶川台地倾斜观测数据和GNSS基线变化的分析,及与区域地震的Benioff蠕变关系的讨论,可得到以下结论:
1)震中区汶川台地倾斜仪在2004年底可观测到倾斜减速现象,2007年底至汶川地震发生未检测到显著的指数型加速异常变化,这可能反映了大震前震中区变形的一个常态特征。
2)广州-泸州GNSS基线加速缩短与Benioff蠕变亏损异常具有较高的相关性,相关系数为0.89。自2005年初开始,广州-泸州基线开始加速缩短,持续时间达2.5年,对应的震级估计为7.9级。与汶川地震震级相当,反映了该基线加速缩短与汶川地震的应变积累过程有一定关系。同期,地震活动也出现长期的平静,Benioff蠕变出现持续亏损异常。两者均反映了汶川地震前的区域应力应变场变化特点。
3)周边大地震发生对川滇地区的应力应变环境影响有明显差异。大地震除引起发震断层附近出现同震形变及震后余滑外,还会引起大范围的应力松弛效应。通过汶川台地倾斜及广州-泸州等基线变化特征分析可知,昆仑山大地震后,变形速率未有明显变化,Benioff蠕变释放速率较为稳定;而苏门答腊地震的发生对川滇地区的应力应变场及区域地震活动的影响显著,并加速了汶川地震的孕育发生过程。
http://ch.whu.edu.cn/cn/article/doi/10.13203/j.whugis20220315
-
表 1 GPS+GLONASS非差非组合PPP数据处理策略
Table 1 Data Processing Strategy of Undifferenced and Uncombined GPS+GLONASS PPP
项目 处理策略 采样间隔/s 30 观测值 GPS: L1、 L2、 L5GLONASS: L1、L2、 L3 参数估计方法 前向卡尔曼滤波 截止高度角/(°) 10 观测值权值分配 高度角模型 潮汐 (海潮、固体潮、极潮)模型改正 卫星天线相位中心改正 GPS/GLONASS L1、L2频点采用IGS 14天线文件推荐值,GPS L5和GLONASS L3频点采用L2的推荐值 接收机天线相位中心改正 GPS/GLONASS L1、L2频点采用IGS 14天线文件推荐值,GPS L5和GLONASS L3频点采用L2的推荐值 卫星星历和钟差 采用德国地学中心提供的精密星历和精密钟差 对流层延迟 先验模型改正+随机游走建模,功率谱密度1.7×10-7 m2/s 电离层延迟 随机游走,功率谱密度为1.7×10-5 m2/s 模糊度 无周跳发生的连续观测弧段,常数估计 接收机钟差 白噪声估计,噪声大小3×105 m AR方法 部分AR 表 2 用户端测试测站信息
Table 2 Station Information of User Side
测站 接收机 天线 测站 接收机 天线 BRAZ TRIMBLE NETR9 TRM57971.00 NONE GENO LEICA GR30 LEIAR20 NONE BRUX SEPT POLARX5TR JAVRINGANT_DM NONE HERS SEPT POLARX5TR LEIAR25.R3 NONE BSHM JAVAD TRE_3 DELTA TRM59800.00 SCIS HOFN LEICA GR50 LEIAR25.R4 LEIT CEBR SEPT POLARX5TR SEPCHOKE_B3E6 NONE KIRU SEPT POLARX5 SEPCHOKE_B3E6 SPKE DLF1 TRIMBLE NETR9 LEIAR25.R3 LEIT REDU SEPT POLARX5 SEPCHOKE_B3E6 SPKE FAIR JAVAD TRE_G3TH DELTA ASH701945G_M JPLA VILL SEPT POLARX5 SEPCHOKE_B3E6 SPKE GANP TRIMBLE ALLOY TRM59800.00 SCIS ESRT SEPT POLARX5 AOAD/M_T DUTD 表 3 静态GPS/GLONASS三频非组合PPP-AR定位偏差统计
Table 3 Statistical Results of Position Errors of GPS/GLONASS Triple-Frequency PPP-AR Static Experiments
方案 平均AR率/% 平均TTFF/min 平均收敛时间/min 各方向定位偏差/mm E N U 3D 方案一 32.5 14.3 30.4 37.4 50.3 方案二 99.5 14.6 15.5 6.0 11.9 23.6 27.1 方案三 99.7 12.5 11.3 3.1 3.6 11.4 12.4 方案四 99.7 12.3 10.9 2.4 2.3 9.2 9.8 表 4 仿动态GPS/GLONASS三频非组合PPP-AR定位偏差统计
Table 4 Statistical Results of Position Errors of GPS/GLONASS Triple-Frequency PPP-AR Simulated Dynamic Experiments
方案 平均AR率/% 平均TTFF/min 各方向定位偏差/mm E N U 3D 方案一 17.4 35.0 40.3 56.1 方案二 99.2 27.9 14.5 22.2 38.8 46.5 方案三 99.5 26.1 20.4 18.8 46.0 53.8 方案四 99.6 12.9 12.7 12.9 34.3 38.9 -
[1] Hein G. Status, Perspectives and Trends of Satellite Navigation[J].Satellite Navigation,2020,1(1): 22.
[2] Montenbruck O, Steigenberger P, Prange L, et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS): Achievements, Prospects and Challenges [J]. Advances in Space Research, 2017, 59(7):1671-1697.
[3] 曹新运,王坚. GPS三频非差观测值探测与修复周跳[J].武汉大学学报(信息科学版), 2014, 39(4):450-456. Cao Xinyun, Wang Jian. Cycle-Slip Detection and Repair Using GPS Triple-Frequency Un-differen‑ced Observations[J]. Geomatics and Information Science of Wuhan University, 2014, 39(4): 450-456.
[4] Geng J, Guo J, Meng X, et al. Speeding up PPP Ambiguity Resolution Using Triple-Frequency GPS/BeiDou/Galileo/QZSS Data [J]. Journal of Geodesy, 2020, 94(1):1-15.
[5] Pan L, Zhang X, Guo F, et al. GPS Inter-frequency Clock Bias Estimation for Both Uncombined and Ionospheric-Free Combined Triple-Frequency Precise Point Positioning [J]. Journal of Geodesy, 2018, 93(4):473-487.
[6] Fan L, Shi C, Li M, et al. GPS Satellite Inter-frequency Clock Bias Estimation Using Triple-Frequency Raw Observations[J]. Journal of Geodesy, 2019, 93(12):2465-2479.
[7] Pan L, Jiang X, Zhang X, et al. GPS + Galileo + BeiDou Precise Point Positioning with Triple-Frequency Ambiguity Resolution[J]. GPS Solutions, 2020, 24(3): 1-13.
[8] 赵齐乐, 陶钧, 郭靖, 等. 广域瞬时厘米级精密单点定位和服务系统[J]. 武汉大学学报(信息科学版), 2023, 48(7): 1058-1069. Zhao Qile, Tao Jun, Guo Jing, et al. Wide-Area Instantaneous cm-Level Precise Point Positioning: Method and Service System[J]. Geomatics and Information Science of Wuhan University, 2023, 48(7): 1058-1069.
[9] Zaminpardaz S, Teunissen P J G, Nadarajah N. GLONASS CDMA L3 Ambiguity Resolution and Positioning[J].GPS Solutions,2017,21(2):535-549.
[10] Zaminpardaz S, Teunissen P J G, Khodabandeh A.GLONASS-Only FDMA+CDMA RTK: Performance and Outlook[J].GPS Solutions,2021,25(3): 1-12.
[11] Zhang F, Chai H, Li L, et al. Understanding the Characteristic of GLONASS Inter-frequency Clock Bias Using Both FDMA and CDMA Signals[J]. GPS Solutions, 2022, 26(2): 63.
[12] Ge M, Gendt G, Rothacher M, et al. Resolution of GPS Carrier-Phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations [J]. Journal of Geodesy, 2008, 82(7): 389-399.
[13] 闫忠宝,张小红.GNSS非组合PPP部分模糊度固定方法与结果分析[J]. 武汉大学学报(信息科学版), 2022, 47(6): 979-989. Yan Zhongbao, Zhang Xiaohong. Partial Ambiguity Resolution Method and Results Analysis for GNSS Uncombined PPP[J]. Geomatics and Information Science of Wuhan University, 2022, 47(6): 979-989.
[14] Geng J, Tfferle F N, Shi C, et al. Ambiguity Resolution in Precise Point Positioning with Hourly Data [J]. GPS Solutions, 2009, 13(4): 263-270.
[15] Geng J, Bock Y. Triple-Frequency GPS Precise Point Positioning with Rapid Ambiguity Resolution [J]. Journal of Geodesy, 2013, 87(5): 449-460.
[16] Guo F, Zhang X, Wang J, et al. Modeling and Assessment of Triple-Frequency BDS Precise Point Positioning [J]. Journal of Geodesy, 2016, 90(11): 1223-1235.
[17] Gu S,Lou Y,Shi C,et al.BeiDou Phase Bias Estimation and Its Application in Precise Point Positioning with Triple-Frequency Observable [J]. Journal of Geodesy, 2015, 89(10): 979-992.
[18] 李浩东, 赵齐乐, 陶钧, 等. 北斗三号卫星FCB估计及其模糊度固定[J]. 武汉大学学报(信息科学版), 2022, 47(9): 1439-1446. Li Haodong, Zhao Qile, Tao Jun, et al. FCB Estimation and Ambiguity Resolution of BDS-3[J]. Geomatics and Information Science of Wuhan University, 2022, 47(9): 1439-1446.
[19] Li P, Zhang X, Ge M, et al. Three-Frequency BDS Precise Point Positioning Ambiguity Resolution Based on Raw Observables [J].Journal of Geodesy, 2018, 92(12): 1357-1369.
[20] Li X, Li X, Liu G, et al. Triple-Frequency PPP Ambiguity Resolution with Multi-constellation GNSS: BDS and Galileo [J]. Journal of Geodesy, 2019, 93(8):1105-1122.
[21] Zhou F, Dong D, Ge M, et al. Simultaneous Estimation of GLONASS Pseudorange Inter-frequency Biases in Precise Point Positioning Using Undifferen‑ced and Uncombined Observations [J]. GPS Solutions, 2017, 22(1): 1-14.
[22] Montenbruck O, Hugentobler U, Dach R, et al. Apparent Clock Variations of the Block IIF-1 (SVN62) GPS Satellite [J]. GPS Solutions, 2012, 16(3):303-313.
[23] Zhang F, Chai H, Li L, et al. Estimation and Analysis of GPS Inter-frequency Clock Biases from Long-Term Triple-Frequency Observations [J]. GPS Solutions, 2021, 25(4):126.
[24] Zhang F, Chai H, Li L, et al. Understanding the Characteristic of GLONASS Inter-frequency Clock Bias Using both FDMA and CDMA Signals [J]. GPS Solutions, 2022, 26(2):63.
[25] Liu Y, Song W, Lou Y, et al. GLONASS Phase Bias Estimation and Its PPP Ambiguity Resolution Using Homogeneous Receivers [J]. GPS Solutions, 2017, 21(2): 427-437.
-
期刊类型引用(11)
1. 祝会忠,郑建行,路阳阳. 一种多频多系统部分模糊度固定算法. 测绘科学. 2024(01): 1-14 .  百度学术
百度学术
2. 祝会忠,邓小松,范佳宝,苑晓峥. 低成本GNSS终端多普勒平滑伪距定位算法. 导航定位学报. 2024(03): 8-15 .  百度学术
百度学术
3. 祝会忠,孙沐凡,李军. GNSS低成本智能终端抗差自适应差分定位算法. 导航定位学报. 2024(06): 10-19 .  百度学术
百度学术
4. 卢春,何祖祺,刘友谊,陈川. 基于EKF算法与卫星导航的民航货运高精度定位系统研究. 计算技术与自动化. 2024(04): 22-28 .  百度学术
百度学术
5. 龚博. 一种顾及载体运动速度的平滑滤波方法. 长江信息通信. 2023(02): 57-60 .  百度学术
百度学术
6. 郭迟,卢飞,邓辰龙,唐卫明,罗亚荣. 利用等价消去原理实现实时动态单点定位快速可靠收敛. 武汉大学学报(信息科学版). 2023(07): 1117-1125 .  百度学术
百度学术
7. 傅鑫榕,王甫红,郭磊,栾梦杰,祝浩祈. 不同电离层模型对智能手机实时PPP精度的影响分析. 测绘地理信息. 2023(06): 26-31 .  百度学术
百度学术
8. 祝会忠,范佳宝,李军. 低成本GNSS终端的抗差RTK定位性能研究. 测绘科学. 2023(12): 1-9 .  百度学术
百度学术
9. 刘路,郭金运,周茂盛,鄢建国,纪兵,赵春梅. GNSS广播星历轨道和钟差精度分析. 武汉大学学报(信息科学版). 2022(07): 1122-1132 .  百度学术
百度学术
10. 王颖喆,胡捷,陶贤露,刘万科,朱锋. Android智能手机双频GNSS伪距差分动态定位性能分析. 导航定位与授时. 2021(05): 103-110 .  百度学术
百度学术
11. 王颖喆,陶贤露,朱锋,刘万科,张小红,吴明魁. 利用智能手机实现GNSS原始观测值的高精度差分定位. 武汉大学学报(信息科学版). 2021(12): 1941-1950 .  百度学术
百度学术
其他类型引用(9)






 下载:
下载: