Simulation Analysis of Inverting Regional Surface Mass Variations Using GNSS Vertical Displacement
-
摘要: 连续密集的全球导航卫星系统(global navigation satellite system, GNSS) 地表形变监测为反演精细的区域地表质量变化提供了有效技术手段。针对格林函数方法反演区域地表质量变化的病态问题,给出了一种改进的正则化拉普拉斯约束矩阵,讨论了广义交叉检验(generalized cross-validation, GCV)方法在病态法方程正则化参数选取中的适应性,并通过数值模拟分析了GNSS垂直位移的噪声水平和测站数量及分布对反演结果的影响。结果表明:(1)给出的正则化拉普拉斯矩阵相比传统的拉普拉斯矩阵能更有效抑制边缘效应的影响;(2)GCV方法可以有效地确定最优正则化参数,其反演结果与均方根误差(root mean square error, RMSE)最小方法的反演结果符合较好;(3)GNSS垂直位移的噪声水平越小, 测站数越多,反演结果越好,并且在测站数达到一定的条件下,均匀分布测站与随机分布测站的反演结果精度相当。
-
关键词:
- 地表垂直位移 /
- 区域地表质量变化 /
- 格林函数方法 /
- 模拟分析 /
- Tikhonov正则化
Abstract:Objectives Continuous and dense global navigation satellite system (GNSS) surface deformation data provide an effective tool to invert refined regional surface mass variations. However, the factors influencing the reliability of GNSS inversion results need to be further studied, such as regularization (including the construction of regularization matrix and determination of optimal regularization parameter), observation noise and distribution of GNSS stations.Methods First, we proposed an improved regularized Laplacian constraint matrix and discussed the adaptability of the generalized cross-validation (GCV) method in selecting the regularization parameter of ill-posed equations for inversion of regional surface mass variations based on the loading Green's function theory. Second, we compared the effects of different constraint matrices and constraint methods on the GNSS inversion results. Third, we further investigated the influences of different noise levels of GNSS vertical displacement, the number and distribution of GNSS stations on the inversion results.Results (1) The regularized Laplacian matrix in this paper can better suppress the edge effects than the traditional Laplacian matrix. (2) The GCV method can effectively determine the optimal regularization parameter, and the inversion results are in good agreement with those solved by the root mean square error (RMSE) criterion. (3) If there are enough GNSS stations and the observation accuracy is high enough in the studied area, the inversion results will be more reliable. Meanwhile, the accuracy of inversion results for uniformly distributed stations is comparable to that of randomly distributed stations when the number of stations is large enough.Conclusions The improved regularized Laplacian matrix and the GCV method can improve the reliability of GNSS inversion results, which can guide the inversion of surface mass variations using measured GNSS data. -
中国山地丘陵区约占国土面积的65%,地质条件复杂,构造活动频繁,崩塌、滑坡、泥石流等突发性地质灾害点多面广、防范难度大,是世界上地质灾害最严重、受威胁人口最多的国家之一。目前,已发现全国共有地质灾害隐患点近30万处,威胁约2 000万人的生命安全和4 500亿元的财产安全。
面对严峻复杂的地质灾害防治形势,中国自20世纪90年代起,先后开展了系统全面的地质灾害详细调查和多轮针对灾害隐患的拉网式、地毯式排查,每年汛期不断巡查,并在此基础上建立了较为完善的群测群防体系。但近年来,中国仍不断有灾难性的地质灾害事件发生,代表性的有2017-06-24四川茂县叠溪镇新磨村滑坡,瞬间将整个村庄几乎掩埋,造成83人死亡和失踪;2018-10西藏雅鲁藏布江米林段色东普沟先后两次发生冰崩-碎屑流-堰塞堵江事件;2018-10和2018-11西藏江达县波罗乡白格村也先后两次发生大型滑坡-堰塞堵江事件。这些事件不仅造成了惨重的生命财产损失,而且引起了社会的广泛关注和国家的高度重视。事后调查发现,这些导致灾难性后果的地质灾害70%以上都不在已知的地质灾害隐患点范围内,其主要原因在于:灾害源区地处大山中上部,多数区域人迹罕至,且被植被覆盖,具有高位、隐蔽性特点,传统的人工排查和群测群防在此类灾害面前已无能为力,传统手段很难提前发现此类灾害隐患。因此,如何提前发现和有效识别出重大地质灾害的潜在隐患并加以主动防控,已成为近期地质灾害防治领域集中关注的焦点和难点。
2018-10-10,习近平总书记主持召开中央财经委员会第3次会议,明确指出:“要建立高效科学的自然灾害防治体系,提高全社会自然灾害防治能力。”并提出推动建设“九大工程”,其中包括:实施灾害风险调查和重点隐患排查工程,掌握风险隐患底数;实施自然灾害监测预警信息化工程,提高多灾种和灾害链综合监测、风险早期识别和预报预警能力。2018年,新组建的自然资源部和应急管理部先后多次召开专题会议,讨论了地质灾害防治问题。自然资源部陆昊部长提出地质灾害防治的“四步”工作方案,即研究原理、发现隐患、监测隐患、发布预警。同时强调,当前防范地质灾害的核心需求是要搞清楚“隐患点在哪里”“什么时候可能发生”。为此,本文围绕这一核心需求,重点探讨如何利用天-空-地一体化的多源立体观(探)测技术实现重大地质灾害隐患的早期识别和监测预警,提升主动防范能力和水平。
1 重大地质灾害隐患及特征
根据国务院2003年颁发的《地质灾害防治条例》,地质灾害是指包括自然因素或者人为活动引发的危害人民生命和财产安全的山体崩塌、滑坡、泥石流、地面塌陷、地裂缝、地面沉降等与地质作用有关的灾害。通常,山体崩塌、滑坡、泥石流的发生具有一定的突发性,被称为突发性地质灾害;而地面塌陷、地裂缝以及地面沉降的形成和发生往往较为缓慢,被称为渐变性地质灾害。人们所关注的地质灾害隐患主要指滑坡、崩塌、泥石流等突发性灾害。而重大地质灾害隐患是指可能造成重大人员伤亡和严重后果的潜在地质灾害隐患点。其中,“重大”主要体现在两方面,一是造成重大人员伤亡,二是造成重大财产和经济损失或广泛的社会影响。近年来,中国造成重大人员伤亡的典型地质灾害事件有:2009-06-05重庆武隆鸡尾山滑坡致79人死亡;2009-08-08莫拉克台风诱发台湾小林村发生滑坡,瞬间将小林村全部掩埋,致使近500人遇难;2010-06-28贵州省关岭滑坡致99人死亡;2010-08-08甘肃舟曲泥石流致1 765人死亡;2013-07-10四川省都江堰五里坡滑坡致161人死亡;2017年茂县新磨村滑坡致83人死亡。近年来,中国造成严重后果的典型地质灾害事件如2000-04-09西藏波密县易贡乡发生巨型山体滑坡-碎屑流-堵江,堵断易贡藏布,形成易贡湖,最大库容达到3×108 m3。两个月后,也即2000-06-10,堰塞坝溃决产生的洪水洪峰流量达到12 000 m3/s,最高洪水位超过50 m,不仅将其下游雅鲁藏布江流域洪水位以下的所有基础设施一扫而光,直接经济损失达上百亿元,而且洪水直达印度,造成巨大的洪涝灾害,冲毁20多座桥梁,致使印度94人死亡和5万人无家可归,产生广泛的国际影响。2018年,西藏米林两次冰崩和白格两次滑坡堰塞堵江事件也产生了广泛的社会影响。尤其是2018-11-03白格第2次滑坡-堰塞堵江事件,因坝体过高(堰塞湖水位可到50 m),堰塞湖库容较大(超过5×108 m3),相关部门不得不通过修建导流槽,主动降低堰塞湖水位。经过人工干预,堰塞体于2018-11-13被冲开,险情得以解除,但下泄的洪水在下游的四川、云南境内造成严重的洪涝灾害,直接经济损失达上百亿元。
重大地质灾害一般具有高位、隐蔽性、远程运动、灾害链效应等特点。高位是指发生地质灾害的源区往往地处山体的中上部斜坡陡峭部位,地质调查人员往往难以到达,有些灾害隐患甚至处于人迹罕至的部位或无人区,传统的人工调查、排查手段已很难发现其隐患的存在。隐蔽性是指西南山区大多植被茂密,斜坡变形迹象和滑坡征兆因被植被遮挡,往往较难发现。远程运动是指大型(一般指体积超过1.0×106 m3)滑坡、崩塌在启动后,往往通过沿途碰撞解体转化为碎屑流,呈远程高速流(运)动,其距离可达数千米乃至数十千米,使灾害危害范围扩大。灾害链效应是指某些灾害在满足一定条件时,可转化为链式灾害。如滑坡转化为碎屑流远距离运动,堵塞河道形成堰塞湖,在上游产生淹没灾害,堰塞湖溃决后还会在下游产生洪涝灾害等,使灾害的影响和损失往往呈数量级放大。在高山峡谷区,大多数村落往往坐落于沟口的大型古老泥石流堆积扇上,而大型沟谷长度一般达数千米乃至数十千米,沟头下雨并形成泥石流,但居住在沟口的人员可能因沟口天气良好,根本察觉不到危险的存在。2010-08-08甘肃舟曲泥石流灾难性事件就是这样造成的。
宏观上讲,地质灾害最容易发生在地质环境脆弱的区域和稳定性相对较差的斜坡部位,这些区域和部位就是需重点关注的潜在地质灾害隐患区。具体地讲,地质灾害隐患一般集中于以下几个区域:
1) 正在变形区。现阶段正在发生变形的区域,显然是最有可能造成失稳破坏和成灾的区域,自然也就成为需重点关注的地质灾害隐患区。
2) 曾经变形区。历史上曾经发生过明显变形,但现阶段已停止变形。如历史上曾经发生过短距离滑动的滑坡,强震导致的震裂山体,或因构造、风化卸荷等因素导致的山体变形开裂等。这些区域一般岩体较为破碎,稳定性差,且往往存在竖向张拉裂缝,具有很好的雨水入渗通道,在强烈外在因素(如强降雨、强震和强烈的人类工程活动等)的作用下,很容易重新变形和失稳破坏。
3) 稳定性较差的斜坡。受构造、卸荷、地震等因素影响,斜坡岩体节理裂隙发育,岩体破碎,尤其是当斜坡中存在有利于岩体滑动的结构面(如顺倾坡外的层面、节理裂隙、软弱夹层等)或斜坡岩体被结构面切割成可变形和滑动的块体时,其稳定性往往较差,容易发生失稳破坏。
4) 大型松散堆积体。各种成因的深厚堆积体(如古老滑坡、崩塌、泥石流堆积体,冰川、冰水堆积体,风积、洪积等),尤其是古老滑坡堆积体,与基岩斜坡相比,其结构松散,稳定性相对较差。当其形态和条件发生改变时,稳定性可能降低,发生变形和失稳破坏。
在明确重大地质灾害隐患的主要类型、特点、主要出露部位后,就可以采取针对性的措施进行地质灾害隐患的早期识别和提前发现,解决“隐患点在哪里”的问题。
2 天-空-地一体化的重大地质灾害隐患识别的“三查”体系
中国地质灾害隐患点多面广,且往往地处高位和被植被覆盖,传统的人工调查和排查已很难发现这些隐患点。为了突破传统人工调查和排查的局限,本文提出可通过构建基于星载平台(高分辨率光学+合成孔径雷达干涉测量技术(interferometric synthetic aperture radar,InSAR))、航空平台(机载激光雷达测量技术(light laser detection and ranging,LiDAR)+无人机摄影测量)、地面平台(斜坡地表和内部观测)的天-空-地一体化的多源立体观测体系,进行重大地质灾害隐患的早期识别。具体地讲,首先借助于高分辨率的光学影像和InSAR识别历史上曾经发生过明显变形破坏和正在变形的区域,实现对重大地质灾害隐患区域性、扫面性的普查;随后,借助于机载LiDAR和无人机航拍,对地质灾害高风险区、隐患集中分布区或重大地质灾害隐患点的地形地貌、地表变形破坏迹象乃至岩体结构等进行详细调查,实现对重大地质灾害隐患的详查;最后,通过地面调查复核以及地表和斜坡内部的观测,甄别并确认或排除普查和详查结果,实现对重大地质灾害隐患的核查(图 1)。地质灾害隐患识别的“三查”体系类似于医学上大病检查和确诊过程,先通过全面体检筛查出重大病患者,再通过详细检查和临床诊断,确诊或排除病患。
2.1 基于光学遥感和InSAR的地质灾害隐患普查
卫星光学遥感技术因其时效性好、宏观性强、信息丰富等特点,已成为重大自然灾害调查分析和灾情评估的一种重要技术手段。早在20世纪70年代,Landsat(分辨率30~80 m)、SPOT(分辨率10~20 m)等中等分辨率的光学卫星影像便被用于地质灾害探测分析。20世纪80年代,黑白航空影像被用于单体地质灾害探测。20世纪90年代以后,IKONOS(分辨率1.0 m)、QuickBird(分辨率0.60 m)等高分辨率的卫星影像被广泛用于地质灾害探测与监测。目前,光学遥感正朝着高空间分辨率(商业卫星分辨率最高为WorldView-3/4 0.3 m)、高光谱分辨率(波段数可达数百个)、高时间分辨率(Planet高分辨率小卫星的重返周期可小于1 d)的方向发展。光学遥感技术在地质灾害研究中的应用逐渐从单一的遥感资料向多时相、多数据源的复合分析发展,从静态地质灾害辨识、形态分析向地质灾害变形动态观测过渡。
地表变形会导致光谱特性变化,由此可利用光学遥感的颜色变化来有效识别地表变形,从而圈定潜在的地质灾害隐患。例如,2016-09-28浙江丽水苏村发生滑坡,瞬间将苏村部分掩埋,导致26人死亡(图 2(a))。滑坡源区地处高位且植被茂盛,但实际上滑坡前其变形在光学遥感影像上已清楚显示。从图 2(b)可以看出,在2000年的遥感影像上就能看到明显的变形迹象,随后变形逐渐发展,空间范围逐渐增大,到2016年滑坡发生前,控制滑坡范围的边界裂缝已清晰可见。
随着光学遥感影像分辨率的不断提高以及卫星数目的不断增多,观测的精度将不断提高,获取影像的时间间隔也将大大缩短,不远的将来就可实现任一地点每天都有一次的卫星影像覆盖,对地质灾害隐患的早期识别和应急抢险将大有裨益。
InSAR技术具有全天候、全天时、覆盖范围广、空间分辨率高、非接触、综合成本低等优点,适宜于开展大范围地质灾害普查与长期持续观测。特别是InSAR具有的大范围连续跟踪微小形变的特性,使其对正在变形区具有独特的识别能力。1996年,法国学者Fruneau等首先证明了合成孔径雷达差分干涉测量技术(differential InSAR, DInSAR)可有效用于小范围滑坡形变监测[1],随后世界各国学者陆续开展了DInSAR在滑坡监测中的应用研究,取得了一些成功案例[2-6]。但在实际应用中,特别是地形起伏较大的山区,星载InSAR的应用效果往往受到几何畸变、时空去相干和大气扰动等因素的制约,具有一定的局限性。此外,应用DInSAR只能监测两时相间发生的相对形变,无法获取研究区域地表形变在时间维上的演化情况,这是由该技术自身的局限性所决定的[7]。针对这些问题,国内外学者在DInSAR的基础上,发展提出了多种时间序列InSAR技术,包括永久散射体干涉测量、小基线集干涉测量、SqueeSAR等[8-13]。这些方法通过对重复轨道观测获取的多时相雷达数据,集中提取具有稳定散射特性的高相干点目标上的时序相位信号进行分析,反演研究区域地表形变平均速率和时间序列形变信息,能够取得厘米级甚至毫米级的形变测量精度。
欧洲(尤其是意大利)已经实现了基于InSAR的全国范围地质灾害隐患普查[14]。近年来,中国将InSAR用于地质灾害的长期监测与隐患早期识别方面也取得了长足进步。图 3是2017年因明显变形而实施应急处置的丹巴县五里牌滑坡的InSAR变形监测结果。从图 3可以看出,利用InSAR不仅可以识别滑坡隐患,还可以较为精确地圈定滑坡边界,定量分析评价滑坡各部位形变的量级和动态演化状况,为滑坡稳定性评判提供了重要手段。尤其是2017年以来,国内外多位学者通过对2017年茂县新磨村滑坡、2018年西藏米林冰崩和白格滑坡等进行分析研究[15-17],结果表明,时序InSAR技术能够有效捕捉滑坡发生前的地表形变,尤其是大面积缓慢蠕滑变形以及滑坡失稳前的加速变形信号[18-19],为提前识别和发现处于正在缓慢蠕滑变形的滑坡隐患提供了非常有效的手段。
2.2 基于机载LiDAR和无人机航拍的地质灾害隐患详查
LiDAR通过集成定姿定位系统和激光测距仪,能够直接获取观测区域的三维表面坐标。机载LiDAR集成了位置测量系统、姿态测量系统、三维激光扫描仪(点云获取)、数码相机(影像获取)等设备。机载LiDAR不仅能够提供高分辨率、高精度的地形地貌影像,同时通过多次回波技术穿透地面植被,利用滤波算法有效去除地表植被,获取真实地面的高程数据信息,为高位、隐蔽性的地质灾害隐患识别提供了重要手段。2017-08-08,九寨沟地震使九寨沟景区惨遭重创,产生了数千处地质灾害,景区被迫关闭。为了查明九寨沟地震区的地质灾害隐患,利用直升机同时搭载三维激光扫描仪和高分辨率光学镜头进行机载LiDAR识别地质灾害隐患的试验研究,图 4是某区域的试验成果。从图 4(a)可以看出,九寨沟景区植被茂盛,通过摄影测量获取的光学影像可清楚地识别出8·8九寨沟地震产生的同震地质灾害,但对植被下的灾害隐患一无所知。利用LiDAR数据去除植被后,获取的数字地表模型(digital surface model,DSM)可清楚地看到植被覆盖下的崩塌松散堆积体(图 4(b))、古老滑坡堆积体、泥石流堆积扇以及较大的震裂山体裂缝,这些都是最容易发生地质灾害的潜在隐患。通过LiDAR去除植被后,生成高精度的DSM,会使掩盖于植被之下的各种山体损伤和松散堆积体暴露无遗,可有效识别隐蔽性灾害,这一特殊功能是其他遥感技术不能比拟的。
随着无人机技术的突飞猛进,利用无人机可进行高精度(厘米级)的垂直航空摄影测量和倾斜摄影测量,并快速生成测区数字地形图、数字正射影像图、数字地表模型、数字地面模型。利用三维DSM不仅可以清楚直观地查看斜坡的历史和现今变形破坏迹象(如地表裂缝、拉陷槽、错台、滑坡壁等),以此发现和识别地质灾害隐患,还可进行地表垂直位移、体积变化、变化前后剖面的计算。例如,在2017-06-24茂县新磨村滑坡的应急处置过程中,由于滑坡源区地处高位,现场人员对山体中上部情况基本一无所知。2017-06-25,通过无人机获取滑坡源区的DSM模型后,发现滑坡右侧存在一个巨大的变形体[15],用DSM模型量测出其体积达4.55×108 m3,与主滑体4.5×108 m3相当,在其后缘存在一宽度达40 m的拉陷槽(图 5(a)),对坡脚数百名应急抢险人员的安全构成严重威胁,为此进行了紧急避让撤离。2017年九寨沟8·8地震后,在短时间内利用无人机航拍生成的三维DSM,发现了多处高位震裂山体和潜在地质灾害隐患(图 5(b)),将相关情况及时上报给现场抗震救灾指挥部后,采取了紧急避让措施。由此可见,利用无人机航拍进行地质灾害隐患识别具有方便快捷、直观形象等特点,必将成为地质灾害隐患识别的重要手段。
2.3 基于地面调查和监测的地质灾害隐患核查
利用空-天遥感手段仅是从外貌形态进行地质灾害隐患的识别,因受多种因素影响,其识别结果并不一定完全正确,可能会出现误判。因此,利用遥感技术识别出来的地质灾害隐患点还需要地质人员到达现场进行逐一调查复核,甄别、确认或排除隐患点,有时还要借助于现场观测和探测手段,才能准确判定。如从地形地貌上像古老滑坡堆积体的区域,有时还得通过物探、槽探等手段,根据坡体结构和物质组成才能确认。另外,在斜坡变形初期,通过InSAR可能会发现其变形迹象,但变形裂缝并不一定会明显显露,此时就需要通过地面观测(如全球导航卫星系统(global navigation satellite system,GNSS)、地基合成孔径雷达系统(ground-based SAR,GBSAR)等)才能确认其是否真的存在变形。这一过程称之为核查,相当于医院医生通过对病人的望闻问切,并结合电子计算机断层扫描、B型超声波检查等检测结果进行综合判断,最后确认或排除病患。
上述地质灾害隐患识别的“三查”体系已在四川、贵州等省进行示范应用,并取得了良好的成效。贵州省利用InSAR、机载LiDAR,对全省高位隐蔽性灾害进行专业排查,发现新的地质灾害隐患点近2 000处,其中高位隐蔽性隐患点近900处。四川省利用InSAR与光学遥感相结合,对6万km2的地质灾害高风险区进行扫面性隐患识别,新发现形变区840处,经现场调查复核,具有明显变形的点超过70%。通过对九寨沟核心景区进行机载LiDAR的示范应用,在面积仅50 km2的区域解译识别出同震地质灾害2 126处,历史灾害83处,潜在隐患26处。2018年金沙江白格滑坡发生后,利用光学遥感和InSAR相结合的手段,短期内在金沙江流域白格滑坡上下游数十千米的区段内,识别出50余处地质灾害隐患,同时确认了几处重大地质灾害隐患。
3 地质灾害的监测预警
利用上述“三查”体系,结合人工调查和排查,便可发现绝大多数地质灾害隐患。但是,发现隐患后该怎么办?这是一个非常现实的问题。本文提出采用如下手段和原则对待和处理新发现的地质灾害隐患。
1) 理性看待。地质的时间尺度和空间尺度与人类都不在一个数量级上,地质学上的时间尺度一般以万年甚至百万年来计算,而人的时间尺度一般以天、年等来计算。这是因为地质体的发展演化一般需要很长时间,且出现隐患并不一定很快就会成灾。
2) 科学评判。对发现的灾害隐患进行科学的分析评判非常重要。通过分析研究,查明灾害隐患的类型、目前所处的发展阶段及其稳定性状况,预测其发展演化趋势,评判其危险性程度和风险,并据此制定有针对性的、科学合理的应对措施。常用的应对措施包括避让搬迁、排危除险、工程治理以及监测预警等。对于已出现明显险情、风险很高的灾害隐患,通过经济效益评估,选择避让搬迁或排危除险等应急处置措施;而对于危害性很大但目前危险性并不太高的灾害隐患,应采取工程治理措施进行主动加固;而对于危害性较大但目前其状况还不够明确的灾害隐患,应通过专业监测来掌握其变形阶段和发展趋势,并据此制定应对方案;而对于一般性的灾害隐患,可直接纳入预案点范围,进行群测群防即可。
3) 监测预警。专业监测预警是科学防范地质灾害的重要手段。一般可先采用时序InSAR监测其目前的变形状况,同时对历史变形进行追踪,判定其变形所处阶段。若变形速率较大或已进入加速变形阶段,则应及时布设地面传感器(如GNSS、裂缝计、雨量计等)和坡体内部传感器(如钻孔倾斜仪、地下水位计等),对地表和内部的变形及其外在影响因素进行精准密集监测,并根据监测结果在实际灾害发生前发出预警信息,以保障受威胁人员的生命财产安全。目前,地质灾害的地面和坡体内部的监测中,各种指标(位移、应力、含水量、水位、雨量等)的现场自动采集、监测数据的远程无线传输等技术均已成熟,其难点在于对现场监测数据的分析处理以及根据监测数据对灾害的发生时间作出及时准确的预警预报。那么,在地质灾害发生前,究竟能不能提前作出预警预报呢?客观地讲,目前地质灾害的预警预报还是一个国际难题,还不可能提前对灾害的发生时间作出准确的预报。但近年来的研究和实践证明,对大多数已进行科学、专业监测的地质灾害体而言,在灾害发生前,提前数小时、数分钟发出预警信息还是可能的。
从保障人民生命安全的角度分析,泥石流灾害的预警相比滑坡、崩塌要简单。一方面,是因为泥石流受水力驱动,有足够的水量(如降雨、冰雪融水等)才会有泥石流发生,所以通过监测降雨量和沟谷水流量可有效预测泥石流;另一方面,泥石流沟谷长度大多为数千米乃至数十千米,泥石流流速一般为每秒数米至数十米左右,泥石流爆发后,其从上游源头区流到下游沟口(村镇大多位于沟口的泥石流堆积扇)一般需要数分钟乃至数十分钟的时间,通过视频、泥位计等手段就可以对泥石流的发生过程进行全面监控。也就是说,除泥石流发生前,可根据当地降雨量和沟谷流量等提前预警外,即使泥石流已经发生,只要进行科学的实时监测预警,也有时间组织沟口人员进行紧急撤离避险。
崩塌、滑坡的预警难度相对较大,尤其是崩塌灾害和某些类型的滑坡,其发生具有突发性,预警难度很大。但大量的滑坡实例表明,滑坡尤其是重力型滑坡(主要受重力作用形成的滑坡,而非地震、降雨、人类工程活动诱发的滑坡),基本都能满足日本学者斋藤提出的3阶段变形规律(图 6)。通过InSAR、GBSAR、GNSS、裂缝计等变形监测手段的持续监测,获取滑坡的变形时间序列曲线,结合监测数据不难判断滑坡当前处于哪一阶段。理论和实践均表明,滑坡进入加速变形阶段是滑坡发生的前提,也是滑坡预警的重要依据。也就是说,若滑坡还处于等速变形阶段,即使有较大的变形速率(一般可达每天数厘米、数分米),也未必会发生滑坡,但一旦进入加速变形阶段,则预示着在未来不久将会发生滑坡。因此,对于新发现的重大滑坡隐患,一般应尽快实施变形监测,掌握滑坡所处的变形阶段,并由此判断滑坡的稳定性和危险性。
基于滑坡的3阶段变形规律以及加速变形对滑坡预警的重要性,文献[20]对滑坡的加速变形阶段进行了细分,并通过统计分析给出了基于变形的滑坡4级综合预警准则(图 7)。滑坡预警级别划分的主要依据,一是根据变形-时间曲线各阶段的特征差异,如曲线斜率(切线角)、加速度、速度增量等;二是根据宏观变形迹象,如地表裂缝的动态发展状况、分期配套特征、滑动面的贯通情况,以及临滑阶段的前兆特征等;三是根据稳定性系数。理论上讲,在滑坡等速变形阶段,其稳定性系数应该在1上下波动,而一旦进入加速变形阶段,其稳定性系数将降低到1以下,临滑阶段其应远小于1。为了使地质灾害监测预警能够实用化和业务化,本文基于全球广域网绘图协议的三维数字地球,研发了地质灾害实时监测预警系统(图 8),实现了现场监测数据的自动采集、远程无线传输、实时自动分析预警和预警信息的自动发送等功能。该系统在2017年曾两次提前数小时成功预警甘肃黑方台黄土滑坡。2018年11月,金沙江白格滑坡堰塞体应急处置过程中,直接使用该系统进行监测预警,对施工现场的几次小规模垮塌均作出了提前预警,保证了施工安全[17]。该系统已用于贵州省地质灾害监测预警的业务化运行,对数百处滑坡隐患进行实时自动监控,一旦某灾害点出现临灾征兆,系统会通过短信等方式将预警信息及时自动发送给相关人员。
4 结论与讨论
中国地质灾害点多面广,不少灾害源区地处高位,且被植被覆盖,仅靠传统的人工调查和排查已很难提前发现和预警重大地质灾害隐患。本文引入现代遥感技术,围绕国家防灾减灾的紧迫需求,拟重点回答和解决地质灾害“隐患点在哪里”“什么时候可能发生”这两个关键问题。得到以下认识:
1) 利用高分辨率的光学遥感影像,通过地形地貌可识别出绝大多数古老滑坡、崩塌堆积体以及泥石流沟,它们在遭受强烈的外界扰动后(如强降雨、强震和强烈人类工程活动),有可能复活或再次发生地质灾害,因而成为常见的地质灾害隐患点。同时,因地表变形会导致光谱特性的变化,可利用光学遥感的颜色变化来有效识别地表变形,圈定潜在的地质灾害隐患。利用多时序遥感影像还可清楚掌握灾害变形的动态演化过程和特征,有助于判断隐患的规模和危险性程度。但光学遥感也存在不足,一是受天气影响明显,如时常因云雾天气而不能获取有效的影像;二是光学影像虽然直观形象,但也容易误判。
2) InSAR具有全天候、全天时工作的特点,尤其是具有大范围连续跟踪观测微小地表形变的能力,是识别和发现正在变形的地质灾害隐患的非常有效和重要的手段,近年来的示范应用效果显著。但InSAR也有一定的局限性,如只能用于识别目前正在发生缓慢变形的地质灾害隐患,对于未变形的地质灾害并不具备识别能力。另外,由于InSAR主要利用相干性原理监测地表形变,复杂地形、植被等都会影响相干性,甚至造成失相干现象。升降轨的拍摄方向也受到很大的限制,有些斜坡方向很难被InSAR拍摄到。同时,目前的InSAR解译并不是非常成熟和流程化,其解译结果的好坏在一定程度上取决于解译人员的经验和专业水平,因此,短期内还达不到全面开花、大范围推广应用的程度。中国应加大对InSAR研究、解译和科学应用方面的人才培养力度。
3) 利用机载LiDAR不仅可以获取高分辨率、高精度的数字高程模型,而且利用去除植被后的真实地形很容易识别和发现古老滑坡崩塌堆积体和其他各种成因的松散堆积体,以及历史上受地震、长期重力作用而发生明显开裂、移位的斜坡岩体,这些都是山区斜坡最脆弱的部位,也是最容易发生地质灾害的潜在隐患区。但目前搭载LiDAR的飞行平台受到较多限制,且实施费用昂贵,无人机摄影测量也面临同样的问题。中国应尽快开展相关方面的专业飞行平台研发和示范应用,增强LiDAR适应复杂环境的能力,降低成本,同时积累相关方面的经验,努力提高扫描和解译精度,提升基于LiDAR的地质灾害隐患识别能力。
4) 光学遥感、InSAR、LiDAR、无人机摄影测量等现代遥感技术都有独自的优势和能力,但也都有各自的条件限制和缺点,所以不能靠单一的技术手段来解决灾害隐患识别问题。为此,本文构建了基于天-空-地一体化的重大地质灾害隐患识别的“三查”体系。该“三查”体系具有“四多”特点:一是多学科交叉融合,其涉及到测量学、工程地质学、遥感地质、计算机技术等多个学科;二是多层次多平台,其综合应用了星载平台、航空平台、地面和坡体内部平台;三是多源数据,包括光学遥感、InSAR、LiDAR、无人机航测以及各种地面和坡体内部观测数据;四是多时序,通过光学遥感、InSAR等手段,不仅可以掌握现状,还可以进行历史追溯和未来长期持续观测,获取多时序数据。“三查”体系遵照从宏观到微观,从区域到区段和单体,分层次分步骤逐步实现复杂山区的地质灾害隐患早期识别和提前发现,为破解“隐患在哪里”这一科技难题提供了解决方案,但这一“技防”措施主要适用于高位隐蔽性的大型地质灾害。中国地质灾害点多面广,对于一般性的地质灾害,人工调查排查和群测群防还是必不可少,得将“技防”和“人防”有机结合,相互补充验证,才能最大限度地发现地质灾害隐患。
5) 地质尺度与人类尺度不在一个数量级,隐患并不一定很快就会成灾。因此,在发现重大地质灾害隐患后,理性对待和科学评判显得非常重要。要在科学评判的基础上,制定科学合理的主动防范措施,如避让搬迁、排危除险、工程治理和监测预警。在大多数情况下,应对重大地质灾害实施专业监测,在掌握其动态演化规律的基础上开展科学预警,在灾害真正发生前发出预警信息,对危险区居民进行疏散避让,保障其生命财产安全。对于非突发性灾害,从理论和技术上均可实现提前预警,但需要进一步推广应用,使地质灾害监测预警工作逐步进入业务化运行阶段。
6) 地质灾害具有“三性”特征。一是存在的客观性,地质灾害会一直存在,人类要学会与灾害共生共处。二是认知的局限性,人类还无法发现所有隐患,更无法彻底消除灾害隐患。三是防灾的长期性,地质灾害防治是一场持久战,很难一劳永逸,只能踏踏实实做好防灾减灾工作,不断降低灾害风险。
-
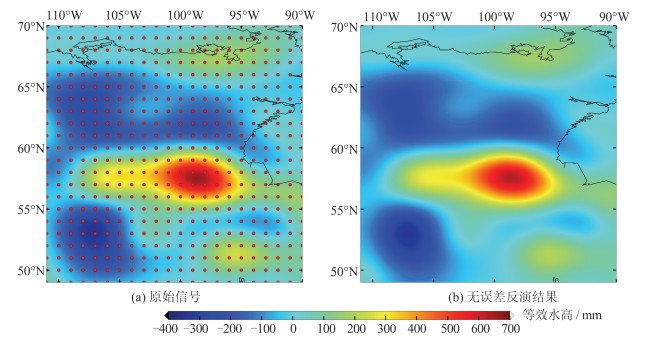
表 1 原始信号和无误差反演结果及残差标准差/mm
Table 1 Statistics of Original Signal, Error-Free Inversion Results and Residuals/mm
项目 最大值 最小值 平均值 标准差 原始信号 660.10 -353.90 9.20 158.90 反演结果 659.70 -353.70 9.30 158.90 残差 18.30 -15.60 0 1.50 表 2 不同正则化约束矩阵对应反演结果的相关系数和残差标准差
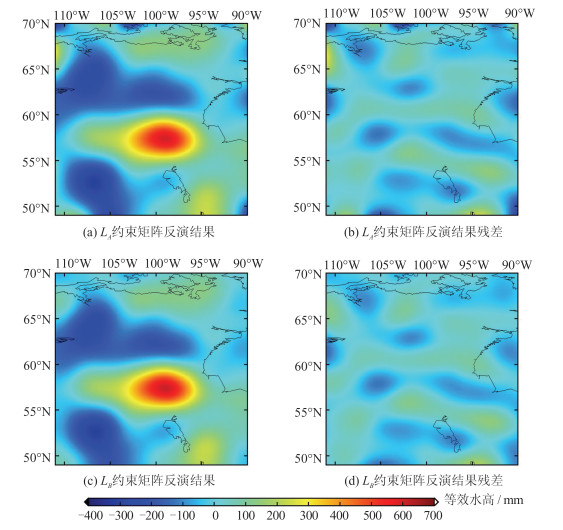
Table 2 Correlation Coefficient and Residual Standard Deviation Estimated from Different Constraint Matrices
约束矩阵 正则化参数λ 相关系数 残差标准差/mm LA 0.08 0.92 62.00 LB 0.30 0.94 52.50 表 3 不同正则化参数反演结果的相关系数和残差标准差
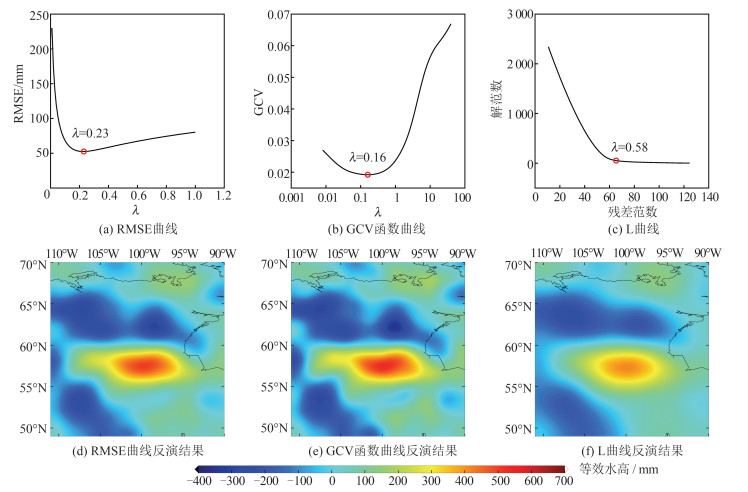
Table 3 Correlation Coefficient and Residual Standard Deviation from Different Regularization Parameters
正则化参数选取方法 正则化参数λ 相关系数 残差标准差/mm RMSE 0.23 0.94 52.40 GCV 0.16 0.94 55.20 L曲线 0.58 0.91 65.90 表 4 不同噪声水平反演结果的相关系数和残差标准差
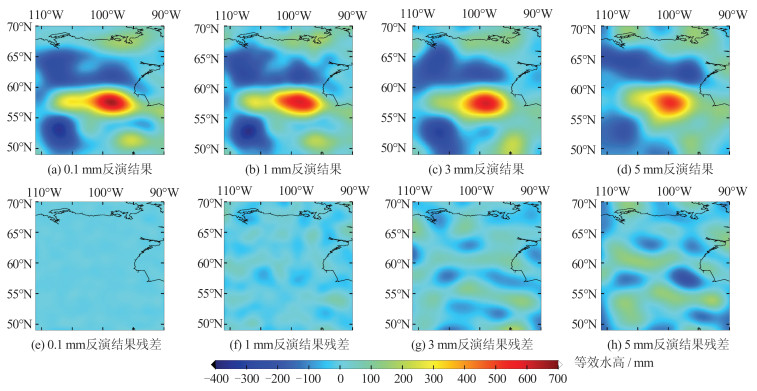
Table 4 Correlation Coefficient and Residual Standard Deviation Corresponding to Different Noise Levels
噪声标准差/mm 垂直位移信噪比 相关系数 残差标准差/mm 0.1 34.70 0.99 5.10 1 14.60 0.98 26.30 3 6.30 0.94 52.50 5 3.50 0.90 71.10 表 5 不同测站分布情况反演结果的相关系数和残差标准差
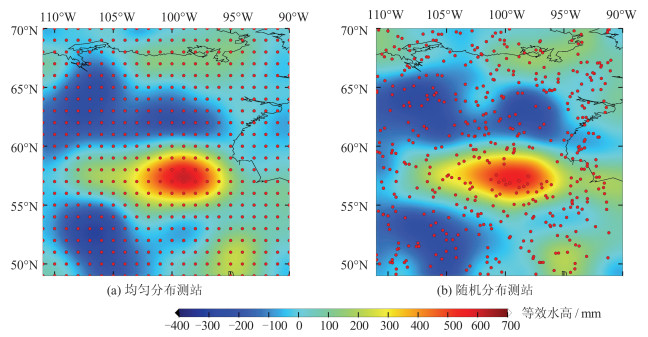
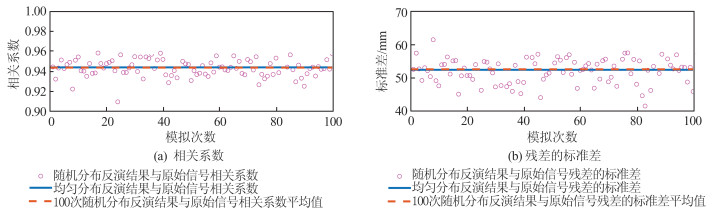
Table 5 Correlation Coefficient and the Residual Standard Deviation Estimated from Different Distributed Stations
测站分布 相关系数 残差标准差/mm 均匀 0.94 52.50 随机 0.95 52.10 表 6 不同测站数反演结果的相关系数和残差标准差
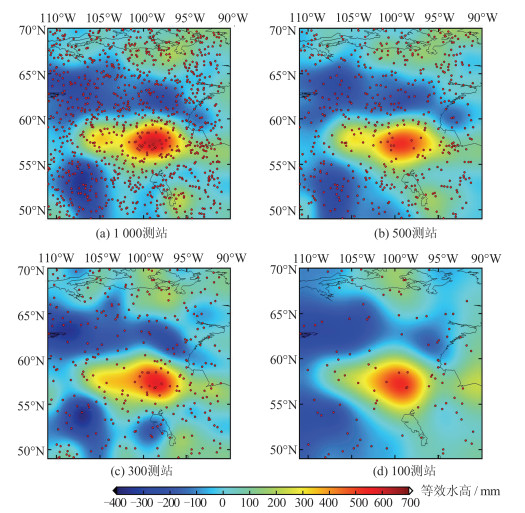
Table 6 Correlation Coefficient and the Residual Standard Deviation Estimated from Number of Different Stations
测站数 相关系数 残差标准差/mm 1 000 0.97 40.20 500 0.95 51.80 300 0.92 62.50 100 0.85 86.00 -
[1] Tapley B D. GRACE Measurements of Mass Variability in the Earth System[J]. Science, 2004, 305(5683): 503-505 doi: 10.1126/science.1099192
[2] Tiwari V M, Wahr J, Swenson S. Dwindling Groundwater Resources in Northern India, from Satellite Gravity Observations[J]. Geophysical Research Letters, 2009, 36(18): 184-201 http://fore.research.yale.edu/files/Tiwari_Wahr_Swenson.pdf
[3] 王星星, 李斐, 郝卫峰, 等. GRACERL05反演南极冰盖质量变化方法比较[J]. 武汉大学学报·信息科学版, 2016, 41(11): 1450-1457 doi: 10.13203/j.whugis20140611 Wang Xingxing, Li Fei, Hao Weifeng, et al. Comparison of Several Filters in the Rates of Antarctic Ice Sheet Mass Change Based on GRACE RL05 Data[J]. Geomatics and Information Science of Wuhan University, 2016, 41(11): 1450-1457 doi: 10.13203/j.whugis20140611
[4] Wang H S, Xiang L W, Jia L L, et al. Load Love Numbers and Green's Functions for Elastic Earth Models PREM, Iasp91, Ak135, and Modified Models with Refined Crustal Structure from Crust 2. 0[J]. Computers & Geosciences, 2012, 49: 190-199 doi: 10.1016/j.cageo.2012.06.022
[5] Argus D F, Fu Y N, Landerer F W. Seasonal Variation in Total Water Storage in California Inferred from GPS Observations of Vertical Land Motion [J]. Geophysical Research Letters, 2014, 41(6): 1971-1980 doi: 10.1002/2014GL059570
[6] Fu Y N, Argus D F, Landerer F W. GPS as an Independent Measurement to Estimate Terrestrial Water Storage Variations in Washington and Oregon [J]. Journal of Geophysical Research: Solid Earth, 2015, 120(1): 552-566 doi: 10.1002/2014JB011415
[7] Wahr J, Khan S A, Tiwari V M, et al. The Use of GPS Horizontals for Loading Studies, with Applications to Northern California and Southeast Greenland [J]. Journal of Geophysical Research: Solid Earth, 2013, 118(4): 1795-1806 doi: 10.1002/jgrb.50104
[8] Heki K. Seasonal Modulation of Interseismic Strain Buildup in Northeastern Japan Driven by Snow Loads[J]. Science, 2001, 293(5527): 89-92 doi: 10.1126/science.1061056
[9] 何思源, 谷延超, 范东明, 等. 利用GPS垂直位移反演云南省陆地水储量变化[J]. 测绘学报, 2018, 47(3): 332-340 https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201803006.htm He Siyuan, Gu Yanchao, Fan Dongming, et al. Seasonal Variation of Terrestrial Water Storage in Yunnan Province Inferred from GPS Vertical Observations[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(3): 332-340 https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201803006.htm
[10] Zhang T Y, Jin S G. Evapotranspiration Variations in the Mississippi River Basin Estimated from GPS Observations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(8): 4694-4701 doi: 10.1109/TGRS.2016.2549364
[11] Jin S G, Zhang T Y. Terrestrial Water Storage Anomalies Associated with Drought in Southwestern USA from GPS Observations[J]. Surveys in Geophysics, 2016, 37(6): 1139-1156 doi: 10.1007/s10712-016-9385-z
[12] Hansen P C. Analysis of Discrete Ill-Posed Problems by Means of the L-Curve[J]. SIAM Review, 1992, 34(4): 561-580 doi: 10.1137/1034115
[13] Golub G H, Heath M, Wahba G. Generalized Cross-Validation as a Method for Choosing a Good Ridge Parameter[J]. Technometrics, 1979, 21(2): 215-223 doi: 10.1080/00401706.1979.10489751
[14] Farrell W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761-797 doi: 10.1029/RG010i003p00761
[15] 程传良. 基于有向树拓扑图的多个体系统能控性分析[D]. 青岛: 青岛大学, 2017 Cheng Chuanliang. Controllability Analysis of Multi-body Systems Based on Directed Tree Topology[D]. Qingdao: Qingdao University, 2017
[16] Dam E R V, Omidi G R. Graphs Whose Normalized Laplacian Has Three Eigenvalues[J]. Linear Algebra and Its Applications, 2011, 435(10): 2560-2569 doi: 10.1016/j.laa.2011.02.005
[17] 顾国华. 基准站GPS连续观测得到的垂直位移时间序列[J]. 地震地质, 2005, 27(2): 332-430 doi: 10.3969/j.issn.0253-4967.2005.02.016 Gu Guohua. Time Series of Vertical Displacements Obtained from Continuous GPS Measurement at Fiducial Stations in the Crustal Movement Observation Network of China[J]. Seismology and Geology, 2005, 27(2): 332-430 doi: 10.3969/j.issn.0253-4967.2005.02.016
-
期刊类型引用(83)
1. 刘晓杰,赵超英,李滨,王文达,张勤,高杨,陈立权,王宝行,郝君明,杨校辉. 基于InSAR技术的甘肃积石山震区活动滑坡识别与动态形变监测. 武汉大学学报(信息科学版). 2025(02): 297-312 .  百度学术
百度学术
2. 黄发明,吴敦筱,常志璐,陈茜,陶杰,蒋水华,周创兵. 滑坡样本缺失下易发性规律和潜在滑坡识别的易发性–InSAR多源信息法. 岩石力学与工程学报. 2025(03): 584-601 .  百度学术
百度学术
3. 张亚楠,郭长宝,杨志华,吴瑞安,闫怡秋. 基于SBAS-InSAR的金沙江上游探戈古滑坡变形特征与影响因素分析. 工程地质学报. 2025(01): 186-200 .  百度学术
百度学术
4. 李广,汤明高,张明礼,左炙坪,帅奕垚. 植被覆盖对季节冻土区黄土斜坡水热变化及稳定性影响. 干旱区资源与环境. 2024(01): 133-142 .  百度学术
百度学术
5. 龚翔,许强,蒲川豪,陈婉琳,修德皓,纪续. 兰州新区平山造城竣工后地表形变InSAR时序监测与分析. 武汉大学学报(信息科学版). 2024(02): 236-245 .  百度学术
百度学术
6. 李泽润,喜文飞,赵子龙,刘海红,张玉英,张莉婷. SBAS-InSAR技术在昆明高铁南站山体形变监测中的应用. 测绘通报. 2024(01): 150-154 .  百度学术
百度学术
7. 李启亮,孙永彬,王诜,汪冰,邓国武,张策. 基于InSAR技术溪洛渡库区活动滑坡形变特征研究. 矿产勘查. 2024(02): 311-319 .  百度学术
百度学术
8. 邓斐,张双成,樊茜佑,牛玉芬,惠文华,司锦钊,吴文辉. 时序InSAR用于滑坡灾前二维形变追溯与灾后风险评价. 测绘科学. 2024(01): 67-78 .  百度学术
百度学术
9. 沙仙武,张亦海,谢启源. 高寒高海拔地区某排土场边坡滑坡模式分析与雷达监测效果研究. 矿产勘查. 2024(S1): 71-76 .  百度学术
百度学术
10. 陈宝林,李为乐,陆会燕,付豪,周胜森,黄维. 基于SBAS-InSAR的黄河干流军功古滑坡形变分析. 武汉大学学报(信息科学版). 2024(08): 1407-1421 .  百度学术
百度学术
11. 魏统彪,石鹏卿,高子雁,周小龙. 基于DeepLabv3+算法的黄土地区地质灾害隐患形变区识别技术研究. 甘肃科学学报. 2024(04): 18-25 .  百度学术
百度学术
12. 李昊,李叶繁,魏长婧,王磊杰,康利军,姜川. 基于SBAS-InSAR技术的登封市潜在地质灾害识别研究. 河南科学. 2024(08): 1170-1178 .  百度学术
百度学术
13. 董思源,曾昭发,周帅,吴燕冈,赵健维. 极端气候条件下黄土体地球物理灾害探测. 地球物理学进展. 2024(04): 1648-1657 .  百度学术
百度学术
14. 张蕙,张娅娣,师芸. 基于InSAR技术的伊宁县滑坡早期识别. 中国矿业. 2024(10): 131-142 .  百度学术
百度学术
15. 佀传琪,王琛,梁家馨,华建,梁发云. 智慧化技术在城市滨海软土工程的应用前景与挑战. 岩土工程学报. 2024(S2): 216-220 .  百度学术
百度学术
16. 杨芳,丁仁军,李勇发. 基于SBAS-InSAR技术的金沙江流域典型滑坡时空演化特征分析. 测绘通报. 2024(11): 102-107 .  百度学术
百度学术
17. 张敏,郑哲,陈哲锋. 基于PS-InSAR的福建寿宁地区地表形变监测与分析. 测绘通报. 2024(12): 117-122 .  百度学术
百度学术
18. 张娅娣,徐欣. InSAR技术在滑坡识别监测中的应用. 电子技术. 2024(12): 44-46 .  百度学术
百度学术
19. 焦润成,郭学飞,南赟,杨红磊,曹颖,王晟宇,闫驰,韩建锋,马晓雪,赵丹凝,倪璇,马驰. 采空区-滑坡-泥石流链式灾害隐患综合遥感识别与评价. 金属矿山. 2023(01): 73-82 .  百度学术
百度学术
20. 毛正君,石硕杰,王贵荣,李欢,于海泳,孙婕文,张瑾鸽. 基于无人机遥感的区域黄土滑坡识别及发育特征分析. 灾害学. 2023(01): 63-71 .  百度学术
百度学术
21. 朱智富,甘淑,袁希平,张荐铭,王睿博,张晓伦. 融合升降轨InSAR数据的东川区滑坡隐患识别. 地球物理学进展. 2023(01): 137-146 .  百度学术
百度学术
22. 尹玉玲,徐素宁,王军,胡克. 典型黄土丘陵区地质灾害隐患识别与时序监测. 水文地质工程地质. 2023(02): 141-149 .  百度学术
百度学术
23. 王勇,陈岩,王沛,李绍陟,尚军,杨军. 升降轨融合的施工区域InSAR地表形变监测. 大地测量与地球动力学. 2023(05): 487-490 .  百度学术
百度学术
24. 张娅娣,师芸,王佳运,颉昕宇,石龙龙. 新疆伊犁地区滑坡隐患InSAR识别与发育特征研究. 遥感技术与应用. 2023(02): 496-507 .  百度学术
百度学术
25. 胡祥祥,柯福阳,张志山,姚永顺,宋宝,明璐璐,尹继鑫,张海欢. 顾及多动态环境因子的滑坡演化规律研究——以西宁市9大滑坡区为例. 测绘通报. 2023(05): 21-26+43 .  百度学术
百度学术
26. 费新峰,田野,赵超英,刘海敏,陈恒祎. 基于多时相InSAR技术的黄河上游龙羊峡库区不稳定边坡识别与形变监测. 地球科学与环境学报. 2023(03): 578-589 .  百度学术
百度学术
27. 王利,张懿恺,舒宝,许豪,魏拓,雷体俊. 基于特征优选和逐步回归的黄土滑坡监测数据融合改进方法. 地球科学与环境学报. 2023(03): 511-521 .  百度学术
百度学术
28. 邵建鸿,郑万鹏,张斌,杜源,王兴涛,栾纪昊. 基于点云数据的黄土公路边坡病害识别. 岩土工程技术. 2023(03): 320-326 .  百度学术
百度学术
29. 王安迪,李龙起. 结合SBAS-InSAR与离散元模拟的茂县核桃坪滑坡变形破坏趋势分析. 大地测量与地球动力学. 2023(07): 685-691 .  百度学术
百度学术
30. 凌峻,张伟. 基于SBAS-InSAR的南水北调淅川县段沉降监测与分析. 人民珠江. 2023(S1): 207-212 .  百度学术
百度学术
31. 许强,董秀军,朱星,邓博,戴可人. 基于实景三维的天-空-地-内滑坡协同观测. 工程地质学报. 2023(03): 706-717 .  百度学术
百度学术
32. 于冰,胡云亮,刘国祥,罗小军,胡金龙. 时序InSAR反演唐山市二维地表形变时间序列. 测绘科学. 2023(06): 82-94+230 .  百度学术
百度学术
33. 张春宇,郭际明,王鼎,许毅,潘尚毅,乔世雄. 基于Stacking-InSAR的澜沧江营盘镇——苗尾段滑坡隐患识别. 地理空间信息. 2023(09): 93-97 .  百度学术
百度学术
34. 杨沛璋,崔圣华,裴向军,何双,王慧,梁玉飞. 基于SBAS-InSAR和光学遥感影像的大型倾倒变形体变形演化. 地质科技通报. 2023(06): 63-75 .  百度学术
百度学术
35. 尹勇,史先琳,钟佳宏,高宏伟,戴可人. 联合升降轨Sentinel-1A监测攀枝花机场高边坡二维形变. 测绘与空间地理信息. 2023(12): 45-48 .  百度学术
百度学术
36. 徐哈宁,邓居智,肖慧. 基于邻近域特征的堆积层滑坡多维地电信息成像监测技术研究. 地学前缘. 2023(06): 473-484 .  百度学术
百度学术
37. 王君鹭,富志鹏. 基于PS-InSAR技术的黄土高边坡形变监测. 公路交通科技. 2023(11): 27-33+60 .  百度学术
百度学术
38. 祝杰,李瑜,师宏波,刘洋洋,韩宇飞,邵银星,王坦. 鹤岗煤矿区地面沉降时空特征InSAR时间序列监测研究. 中国地震. 2023(03): 596-608 .  百度学术
百度学术
39. 许强,陆会燕,李为乐,董秀军,郭晨. 滑坡隐患类型与对应识别方法. 武汉大学学报(信息科学版). 2022(03): 377-387 .  百度学术
百度学术
40. 姚闯闯,姚鑫,顾畛逵,任开瑀,周振凯. 基于InSAR识别的黄土高原活动性地质灾害发育规律分析. 地质力学学报. 2022(02): 257-267 .  百度学术
百度学术
41. 谭超,薛廉,齐得旭. 利用多InSAR技术分析某天然气管道填方区形变. 测绘地理信息. 2022(03): 61-64 .  百度学术
百度学术
42. 许广河,何小锋,王国瑞,扈志勇,程霞,李小琼. 黄河流域宁夏(西吉县)段滑坡灾害的InSAR识别及成因分析. 测绘通报. 2022(06): 104-107 .  百度学术
百度学术
43. 廖军,吴彩燕,王立娟,谭秋焰,朱新婷. 基于时序InSAR的滑坡早期识别——以贵州省水城县为例. 自然灾害学报. 2022(03): 251-260 .  百度学术
百度学术
44. 刘小松,冯婧. 山西某县地质灾害隐患的高分辨率时序InSAR识别. 测绘技术装备. 2022(02): 76-81 .  百度学术
百度学术
45. 刘陈伟,蒋亚楠,廖露,燕翱翔,罗袆沅. 黑方台主要形变区的SBAS-InSAR识别与分析. 测绘科学. 2022(05): 56-65 .  百度学术
百度学术
46. 常宏. 三峡库区潜在顺层岩质滑坡识别的宏观判据. 华南地质. 2022(02): 265-272 .  百度学术
百度学术
47. 何秀凤,高壮,肖儒雅,罗海滨,贾东振,章浙涛. InSAR与北斗/GNSS综合方法监测地表形变研究现状与展望. 测绘学报. 2022(07): 1338-1355 .  百度学术
百度学术
48. 董继红,马志刚,梁京涛,刘彬,赵聪,曾帅,鄢圣武,马晓波. 基于时序InSAR技术的滑坡隐患识别对比研究. 自然资源遥感. 2022(03): 73-81 .  百度学术
百度学术
49. 高星月,王世杰,高鹏程. D-InSAR与随机森林模型耦合的活动性滑坡识别方法探究. 中国地质灾害与防治学报. 2022(05): 102-108 .  百度学术
百度学术
50. 喜文飞,赵子龙,李国柱,周定义,杨正荣. SBAS-InSAR技术与无人机影像融合的滑坡变形监测. 测绘通报. 2022(10): 1-6 .  百度学术
百度学术
51. 黄海峰,薛蓉花,赵蓓蓓,易武,邓永煌,董志鸿,柳青,易庆林,张国栋. 孕灾机理与综合遥感结合的三峡库首顺层岩质滑坡隐患识别. 测绘学报. 2022(10): 2056-2068 .  百度学术
百度学术
52. 刘纪平,梁恩婕,徐胜华,刘猛猛,王勇,张福浩,罗安. 顾及样本优化选择的多核支持向量机滑坡灾害易发性分析评价. 测绘学报. 2022(10): 2034-2045 .  百度学术
百度学术
53. 董建军,梅媛,闫斌,刘士乙. 高海拔排土场边坡安全稳定性D-InSAR监测. 安全与环境学报. 2022(05): 2514-2523 .  百度学术
百度学术
54. 弓永峰,王辉,吴学华,张佳,刘君. 基于时序InSAR的宁夏西吉县滑坡灾害隐患识别. 安全与环境工程. 2022(06): 114-121 .  百度学术
百度学术
55. 邹俊,武斌,刘义,艾力丰,陈宁. InSAR技术在西南山区管道沿线地质灾害监测中的应用. 四川地质学报. 2022(S2): 178-182 .  百度学术
百度学术
56. 余斌,李松,谢凌霄,贾洪果,亢邈迒,刘雨鑫,廖明杰,张瑞. 改进TS-InSAR方法的白格滑坡灾前-灾后形变演化特征分析. 测绘通报. 2022(11): 8-12 .  百度学术
百度学术
57. 吴琼,葛大庆,于峻川,张玲,李曼,刘斌,王艳,马燕妮,刘宏娟. 广域滑坡灾害隐患InSAR显著性形变区深度学习识别技术. 测绘学报. 2022(10): 2046-2055 .  百度学术
百度学术
58. 凌晴,张勤,张静,瞿伟,孔令杰,朱丽,张金辉. 融合工程地质资料与GNSS高精度监测信息的黑方台党川黄土滑坡稳定性研究. 测绘学报. 2022(10): 2226-2238 .  百度学术
百度学术
59. 李晓恩,周亮,苏奋振,吴文周. InSAR技术在滑坡灾害中的应用研究进展. 遥感学报. 2021(02): 614-629 .  百度学术
百度学术
60. 李广,张明礼,叶伟林,王得楷,马昭,安亚鹏. 甘肃黑方台坡面冻融特征及冻结滞水效应分析. 干旱区资源与环境. 2021(06): 117-122 .  百度学术
百度学术
61. 杨成生,董继红,朱赛楠,熊国华. 金沙江结合带巴塘段滑坡群InSAR探测识别与形变特征. 地球科学与环境学报. 2021(02): 398-408 .  百度学术
百度学术
62. 王新刚,刘凯,连宝琴,王家鼎,邱海军,胡胜. 黄土-泥岩滑坡诱发因素及形成机理研究进展. 西北大学学报(自然科学版). 2021(03): 404-413 .  百度学术
百度学术
63. 代聪,李为乐,陆会燕,杨帆,许强,简季. 甘肃省舟曲县城周边活动滑坡InSAR探测. 武汉大学学报(信息科学版). 2021(07): 994-1002 .  百度学术
百度学术
64. 许强,蒲川豪,赵宽耀,何攀,张含悦,刘佳良. 延安新区地面沉降时空演化特征时序InSAR监测与分析. 武汉大学学报(信息科学版). 2021(07): 957-969 .  百度学术
百度学术
65. 方汕澳,许强,修德皓,赵宽耀,李志刚,蒲枫. 基于斜率模型的突发型黄土滑坡失稳时间预测. 水文地质工程地质. 2021(04): 169-179 .  百度学术
百度学术
66. 杨通,南燕云,张智杰,于潇,王效科. 基于主被动遥感协同的山体隆升动态监测研究. 干旱区资源与环境. 2021(10): 178-184 .  百度学术
百度学术
67. 杨通,张智杰,王效科,郭旭东,于潇. 基于PS-InSAR技术监测土壤侵蚀可行性研究. 农业工程学报. 2021(14): 127-134 .  百度学术
百度学术
68. 刘睿,王志勇,高瑞. 时序SAR影像的干旱地区土地利用分类应用. 测绘科学. 2021(10): 90-97 .  百度学术
百度学术
69. 张双成,司锦钊,徐永福,牛玉芬,樊茜佑,朱武,安鹏,郭衍辉. 时序InSAR用于安康膨胀土机场稳定性监测. 武汉大学学报(信息科学版). 2021(10): 1519-1528 .  百度学术
百度学术
70. 王哲,赵超英,刘晓杰,李滨. 西藏易贡滑坡演化光学遥感分析与InSAR形变监测. 武汉大学学报(信息科学版). 2021(10): 1569-1578 .  百度学术
百度学术
71. 焦志平,江利明,牛富俊,郭瑞,周志伟. 藏东冻土区滑坡形变时序InSAR监测分析——以317国道矮拉山为例. 冰川冻土. 2021(05): 1312-1322 .  百度学术
百度学术
72. 李磊,许冲,张中俭,黄远东. 黄土高原滑坡灾害研究综述. 防灾科技学院学报. 2021(04): 1-11 .  百度学术
百度学术
73. 李万林,周英帅. 基于D-InSAR技术的地质灾害和监测预警. 测绘工程. 2021(01): 66-70 .  百度学术
百度学术
74. 高海英,赵争,章彭. 时序InSAR的贵州地质灾害监测. 测绘科学. 2020(07): 91-99 .  百度学术
百度学术
75. 张福浩,朱月月,赵习枝,张杨,石丽红,刘晓东. 地理因子支持下的滑坡隐患点空间分布特征及识别研究. 武汉大学学报(信息科学版). 2020(08): 1233-1244 .  百度学术
百度学术
76. 王智伟,王利,黄观文,韩清清,徐甫,岳聪. 基于BP神经网络的滑坡监测多源异构数据融合算法研究. 地质力学学报. 2020(04): 575-582 .  百度学术
百度学术
77. 姚鑫,邓建辉,刘星洪,周振凯,姚佳明,戴福初,任开瑀,李凌婧. 青藏高原泛三江并流区活动性滑坡InSAR初步识别与发育规律分析. 工程科学与技术. 2020(05): 16-37 .  百度学术
百度学术
78. 武宇,张俊,尹耀. 时序InSAR技术对城建地选址的潜在影响研究. 城市勘测. 2020(05): 10-14 .  百度学术
百度学术
79. LIAN Xu-gang,LI Zou-jun,YUAN Hong-yan,LIU Ji-bo,ZHANG Yan-jun,LIU Xiao-yu,WU Yan-ru. Rapid identification of landslide, collapse and crack based on low-altitude remote sensing image of UAV. Journal of Mountain Science. 2020(12): 2915-2928 .  必应学术
必应学术
80. 贺凯,李滨,赵超英,高杨,陈立权,刘朋飞. 基于易滑地质结构与多源数据差异的岩溶山区大型崩滑灾害识别研究. 中国岩溶. 2020(04): 467-477 .  百度学术
百度学术
81. 蔡杰华,张路,董杰,董秀军,廖明生,许强. 九寨沟震后滑坡隐患雷达遥感早期识别与形变监测. 武汉大学学报(信息科学版). 2020(11): 1707-1716 .  百度学术
百度学术
82. 戴可人,卓冠晨,许强,李振洪,李为乐,管威. 雷达干涉测量对甘肃南峪乡滑坡灾前二维形变追溯. 武汉大学学报(信息科学版). 2019(12): 1778-1786+1796 .  百度学术
百度学术
83. 佘金星,周兴霞,刘飞,黄青伦,董秀军. 丹巴地质灾害隐患早期识别关键技术研究. 测绘. 2019(06): 243-247 .  百度学术
百度学术
其他类型引用(92)






 下载:
下载: