在地质建模中，获得具有高质量的符合特征约束的连续网格，以反映现实几何模型的要求和模拟约束的任务具有重要研究价值。在本文所应用的场景中，每种类型矿体代表一种域，多域复杂矿体建模除了需要有效地生成高质量的多分辨率网格，同时要求处理多域邻接特征。

在矿体结构建模中，显式建模在实际应用中仍然十分广泛，该方法通过一系列矿体轮廓线拼接进行三维重建，可以获得严格按轮廓线约束的三维表面实体。对于单一矿体的轮廓线建模，通过人工调整约束线，总可以生成封闭的不自相交的模型。然而，对于多种矿体轮廓线建模，即使调整线框使轮廓线贴合，在轮廓线拼接的过程中在复杂边界处总是会出现各种相交情况，不利于后期储量计算、工程设计和有限元分析等工作。对于生成的表面模型后期仍然需要对多种矿体进行网格剖分操作。一种可选的方法是对多个矿体分别进行布尔运算，人工分离交叉部分。然而在复杂矿体边界处存在大量交叉情况，工作量大且容易出错；同时，对于交叉部分无法进行中间拟合处理。

改进的基于Delaunay细分的算法首先被应用于二维曲线的重构^[1]，之后被推广到包括平滑表面、多面体结构域、由光滑表面界定的三维域以及由分段光滑表面界定的三维域等的表面重构^[2-8]，并得到了可靠的证明^[9]。已有相关研究对CT扫描的多域三维灰度图进行了三维重建，并应用于科学计算可视化^[10-11]。

本文应用Delaunay细分方法实现了一种适用于多域复杂矿体的网络剖分方法，可以对多种矿体表面模型同时进行网格剖分，利用矿体轮廓线进行特征约束，生成的模型是一种封闭的、没有自相交的和具有多标签的表面网格和体积网格模型。采用改进的多标签细分算法可以对中间域进行分离或通过距离场对中间域进行拟合。最终可以获得具有很好边界拟合特征的分离表面模型，每个子模型之间在边界处很好地贴合在一起。对于体模型，通过去除sliver，可以获得用于后期模拟的高质量连续体网格，很好地处理了多个表面模型交叉边界网格剖分的问题。

1 多域复杂矿体建模

基于线框模型的矿体建模，大部分已有的研究都基于单一矿体进行建模，对于多域的复杂矿体建模目前没有普遍适用的方法。一般的做法是根据线框类型分别对每个子矿体(子域)建模。这种方法的最大问题是多域之间的邻接问题，即无法处理多个子模型之间的贴合问题，模型之间容易产生交叉和空隙。同时模型结果存在大量退化的三角面片。

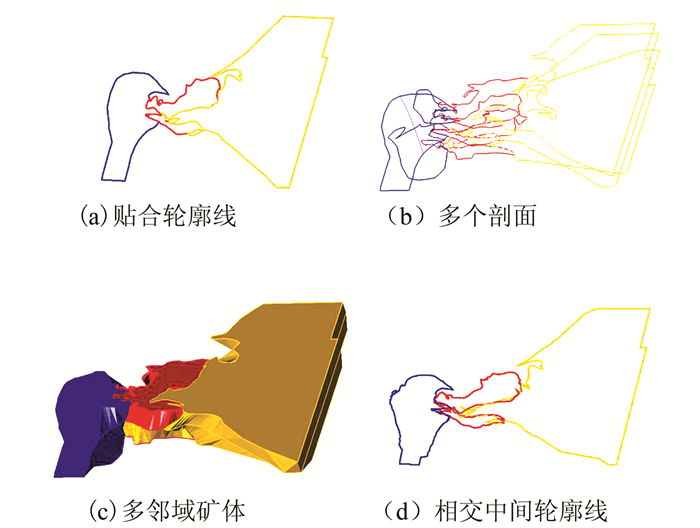
以河北省北洺河铁矿多域矿体建模为例，如图 1(a)所示。建模前先对轮廓线进行处理，使相邻子域的轮廓线很好地贴合在一起。然后采用最小表面积法分别对每个子矿体进行连线框建模，每个子矿体都可以形成一个不自相交的封闭矿体，最终生成的多个矿体表面模型如图 1(c)所示。这种多域模型在中间部分往往容易产生复杂的交叉情况，如图 1(d)所示，无法直接应用于后期设计和计算，需要进行后期处理。

图  1  多域矿体建模存在的问题

Figure  1.  Problems of Multi-domain Orebodies Modeling

下载: 全尺寸图片 幻灯片

同样，多域矿体网格剖分的一般方法是将待剖分的矿体按某种方式人工分解为多个子矿体，然后对每个子矿体分别进行网格剖分。为了避免模型边界的交叉，需要人工分离子矿体的边界面，这种方法无法满足自动网格剖分的要求。

2 算法原理与流程

网格划分算法依赖于约束Delaunay三角剖分来近似域和曲面，以及在Delaunay细分中确保对域的近似精度和对单元的网格质量。

2.1   约束Delaunay三角剖分

在表面重建问题中，对于表面S上采样的有限点集E，在E具有良好采样特征的情况下，希望通过E获得对S的良好近似的表面模型^[9]。

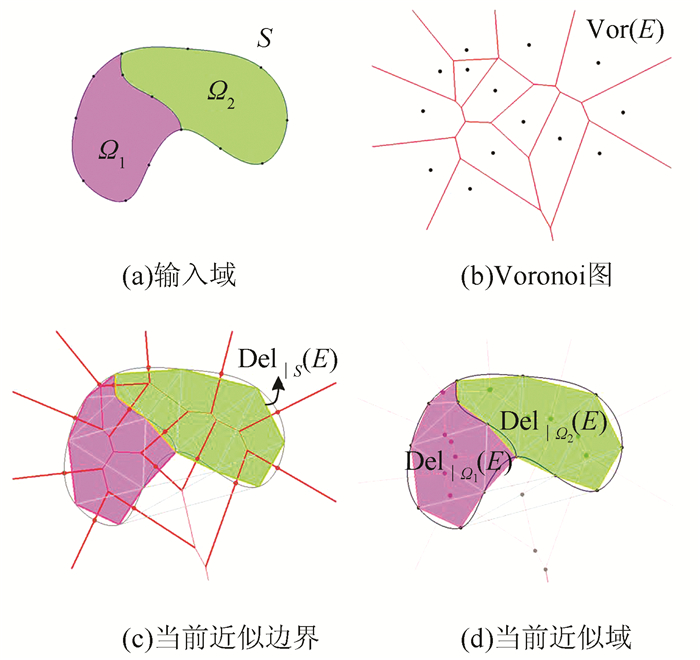
设E={p₁, p₂…p_n}为定义在三维空间中表面S的一组采样点，E的Delaunay三角剖分Del_|S(E)是其Voronoi图的对偶图。根据空圆性质，在任意两点p_i和p_j的Delaunay三角剖分中，只要它们对应的Voronoi单元V(p_i)和V(p_j)存在非空交集，则在两点p_i和p_j间存在一条边。

对于三维空间中的输入域Ω，其边界为S，将E限制于域Ω的Delaunay三角剖分记作Del_|Ω(E)，是由与域Ω相交的对偶Voronoi单元的Delaunay单纯形组成，即Del(E)的子复形。

以二维情况为例，如图 2所示，输入域Ω可以被细分为几个子域，每个子域由Ω_i表示。边界S上的采样点为初始采样点。如图 2(c)所示，限制在边界S上的Delaunay三角剖分由其对偶Voronoi边与边界S相交的Delaunay边组成。同样，如图 2(d)所示，限制在区域Ω上的Delaunay三角剖分由其外心包含在Ω内的Delaunay三角形组成。

图  2  约束Delaunay三角剖分

Figure  2.  Constraint Delaunay Triangulation

下载: 全尺寸图片 幻灯片

基于以上分析，已经有相关研究表明，在一定的假设条件下，只要E是Ω足够密集的采样点集，则Del_|S(E)是边界S的很好近似，Del_|Ω(E)是Ω域的很好近似^[9]。这种近似满足拓扑和几何意义上的一致性：在拓扑上，Del_|Ω(E)与Ω是同胚的；在几何上，Del_|Ω(E)与Ω的Hausdorff距离可以任意小；同时，Del_|Ω(E)可以连续近似地趋近于Ω的法向和曲率。以上这些性质还可以扩展应用到 R ^d维空间上^{[9, 12-13]}。

2.2   Delaunay细分与自适应

如上所述，基于Delaunay细分的网格剖分算法需要对一组点E∈ R³进行采样，并构建限制在Ω上E的Delaunay三角剖分。然后对该初始集合近似进行细分，细分的终止条件是网格剖分满足用户给出的边界面和四面体质量标准^[14-15]。

边界面的标准：最小角度α，用于控制三角面片的形状；最大边长l，用于控制三角面片的大小；边界面facet与三角面片之间的最大距离d，用于控制边界面和细分表面的近似误差，它表示三角面片的外心与相应表面Delaunay球中心之间距离的上限。

四面体标准：四面体外接圆半径与最短边长度之比β，用于控制四面体单元的现状(除了sliver)；最大边长度L，用于控制四面体单元的大小。

因此，网格细分标准由如上所述的5个参数(α, l, d, β, L)给出。对于f∈Del_|S(E)，不满足边界面标准的三角面片为坏的三角面片。对于t∈Del_|Ω(E)，不满足四面体标准的四面体为坏的四面体。

Delaunay细分阶段，主要是根据网格细分标准(α，l，d，β，L)对点集进行增量构造。当它们不满足相应标准时，在Del_|Ω(P)和Del_|S(P)中的元素被认为是坏的。细化过程中通过计算并插入新的顶点(Steiner点)以删除这些坏的元素，直到所有元素满足质量标准。

坏的三角面片f的Steiner点：是三角面片f的表面Delaunay球SDB(f)的球心，如果有多个球，则是其中一个球的球心。

坏的四面体单元t的Steiner点：是四面体单元t的外接球球心。

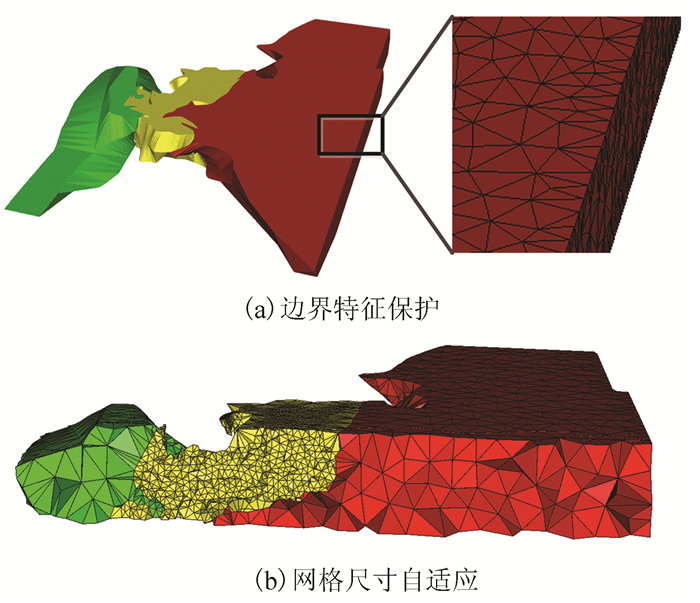
基于Delaunay细分增量构造的特点，为了在感兴趣的区域产生密集网格，用户可自定义自适应尺寸场，构造统一或非均匀的标量场。

对于多域网格剖分，为了突出对某些子域的关注，有时需要获得对特定子域的密集网格，构造一种基于子域标签的自适应尺寸场，可以对不同子域分配不同网格细分标准。

对于单纯的表面重建，为了突出对子域边界的关注，有时需要获得尺寸逐步减小的分级网格，构造一种基于边界距离的距离场的自适应尺寸场，可以获得在边界密集细分而内部逐级细分的网格。

2.3   边界特征保护

一般的Delaunay细化算法无法保证边界中具有特征边和角的邻域，容易造成局部区域失真。如果直接将特征边和角作为约束进行约束剖分，则在具有较小二面角的边界面附近可能造成细分过程无法终止。然而，文献[16-18]证明，如果特征边被保护球保护，则Delaunay细分具有可证明的终止条件。

边界特征保护的基本思想是：在进行Delaunay细化之前，对输入域的一维和零维特征进行采样，用保护球的方式对特征进行采样和保护。然后使用加权Delaunay三角剖分法进行Delaunay细化，保护球作为初始采样点集。

在进行特征保护时，首先保留所有特征角，再按用户指定的密度对特征边进行采样。一般特征边上两个采样点之间的距离不大于三角面片的最大边长度l。将每个保护球b=(p, r)变成加权点(p, r)，并插入到初始点集合E中。Delaunay三角剖分变为加权Delaunay三角剖分，其中欧几里德距离由加权距离代替。

保护球和加权Delaunay三角剖分保证了两个重要的性质。首先，任何受保护边上的两个相邻点之间的线段保持与限制的Delaunay边相连。其次，由于算法永远不会尝试在保护球的联合中插入一个细化点，可以确保细化过程的终止。

2.4   网格优化

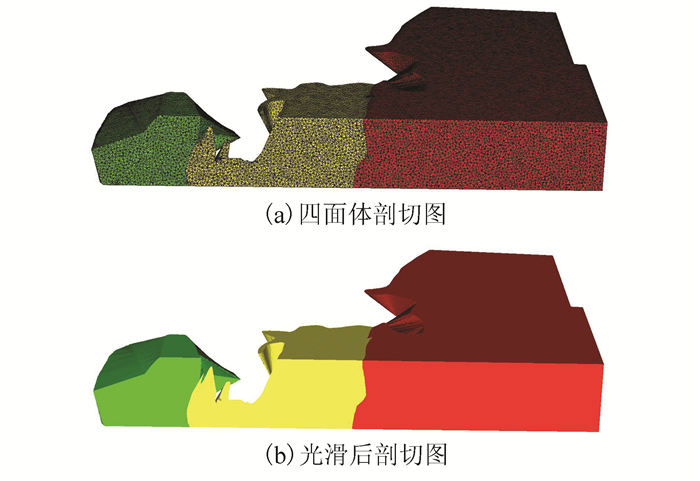
细化过程结束后，所有元素均满足用户设定的边界面和四面体标准，消除了退化四面体中除sliver之外的所有形状不好的四面体^[19-21]。因此，需要使用移除sliver算法从网格中去除具有较小二面角(条子)的退化四面体，进行网格优化。需要注意的是，边界面标准中采用了最小角度α控制三角面片的形状，在表面重建中一般不存在退化的三角面片。

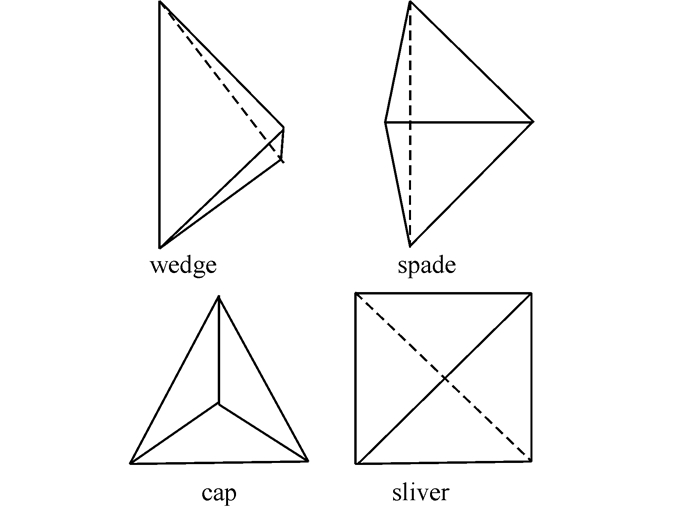
需要进行移除sliver过程的主要原因是，用于控制四面体形状的标准β可以处理除了sliver四面体外任意具有较大半径-边比的准退化四面体。sliver是一种4个顶点靠近一个平面的四面体，并且其对该平面的正交投影是没有短边的凸四边形。sliver在三维Delaunay三角剖分中是很常见的，甚至对于间隔很好的点集也是如此。虽然sliver具有较小的半径-边比，但其纵横比仍然较大，因此其相应四面体单元的形状质量较差。如图 3所示，在4种顶点近似共面、形状质量较差的四面体单元中如wedge、spade、cap、sliver等，其中sliver是唯一一类不具有大的半径-边比的准退化四面体。

图  3  4种顶点近似共面形状质量较差四面体单元

Figure  3.  Four Types of Tetrahedron Cells with Approximate coplanar vertices and poor quality

下载: 全尺寸图片 幻灯片

网格优化过程就是要处理具有较小二面角的四面体，以便消除sliver，改善四面体单元二面角的分布。网格优化一般分为全局优化和局部优化^[22]，全局优化可以大大减少所有sliver的总数，而局部优化则更关注于质量最差的四面体单元。本文采用一种称为条子渗出^[21]的算法，算法的基本思想是将Delaunay三角剖分变为加权的Delaunay三角剖分，其目的是通过用最佳权重重新加权网格顶点来移除sliver，所述最佳权重触发组合变化，从而诱导条子渗出。如果Delaunay三角剖分具有如文献[23]中的比率属性，那么有一个权重的分配，使加权Delaunay三角剖分不包含sliver。

基于以上思想，在Delaunay细化结束之后，采用以上条子渗出的后处理步骤，对四面体单元进行网格优化。其好处是不会影响已经建立好的表面模型，只处理域内的四面体单元。同时，该方法不会产生任何新的顶点，也不移动任何已有的顶点，避免对按当前标准细分的结果产生较大影响。该方法在实践中效果显著，可以生成几乎没有silver的四面体网格单元。

2.5   多域标签算法改进

基于以上分析，单域网格划分算法总体上包括3个主要阶段：初始化阶段、Delaunay细分阶段和优化阶段。本文所实现的算法在单域网格剖分算法的基础上，通过标签对子域进行封装，并对中间域进行分离或通过距离场对中间域进行拟合，从而适应复杂矿体多域网格剖分问题。

将多域网格剖分考虑成一种多标签特征函数F:Z³→J，其中J={0, 1，2…n}是一组标签，0表示空隙，1，2…n表示不同多面体子域的标签。每个标签i对应相应子域的特征函数f_i:Z³→{0, 1}，如果F(p)=i，则f_i(p)=1，否则f_i(p)=0。

在多域网格剖分中，如果存在点p在多个子域的特征函数中满足f_i(p)=1，此时多标签特征函数F(p)的取值存在二义性，则该点对应中间域。中间域的点在三角面片中对应不同子域的边界，在四面体单元中对应不同子域的相交区域。为了消除多标签特征函数的二义性，通过修改特征函数F(p)标签的方法，将子标签分配给父标签进行域分离，或通过距离场计算拟合中间域，使得F(p)=i，保证标签的唯一性，从而达到多域网格剖分的目的。

初始化阶段对多域表面模型的每个子域进行初始点采样。如果需要进行边界特征保护，则把特征点加入初始点集中，对初始点集进行初始Delaunay三角剖分。

Delaunay细化阶段包括两个步骤：表面网格步骤和体积网格步骤。表面网格步骤处理坏的三角面片，并将Steiner点添加到表面上，直到所有三角面片满足标准。体积网格步骤处理坏的四面体单元，并将Steiner点添加到域内或表面上，直到所有四面体单元满足标准。Delaunay细分算法具体过程描述如下：

while存在坏的三角面片或坏的四面体do

if存在坏的三角面片，then

令f为质量最差的三角面片

令p为坏的三角面片f的Steiner点

将p插入采样点集E中

else存在坏的四面体单元t

令c为质量最差的四面体单元t的外接球球心

if存在坏的三角面片f，其表面Delau- nay球包含c，then

令p为坏的四面体单元t的Steiner点

将p插入采样点集E中

else

直接将c插入采样点集E中

end if

end if

更新Del (E)

end while

优化阶段的目的是改善四面体二面角的分布，以获得良好质量的网格。

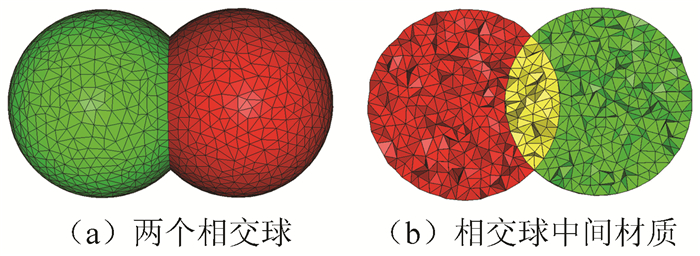
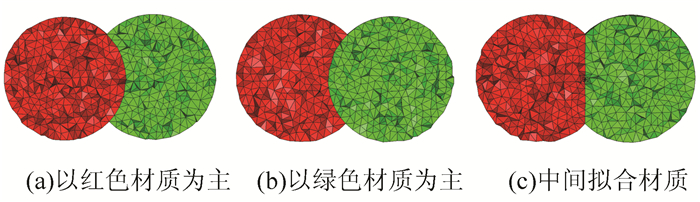
基于以上分析，在算法的任何步骤，Del_|S(E)是表面S的当前近似，Del_|Ω(E)是域Ω的当前近似。以两个相交球为例，如图 4所示，在单域的情况下，在Delaunay细分结束时，Del_|S(E)是Del_|Ω(E)的边界；在多域的情况下，两个相邻四面体的三角形可能来自属于Del_|S(E)的不同子域，不同子域类型通过标签进行区分。对于相交部分域，可以通过修改标签的方法，将子标签分配给父标签进行域分离，也可以通过距离场计算拟合中间部分域。假设红色材质为f₁(p)→{0, 1}，绿色材质为f₂(p)→{0, 1}，多标签特征函数F(p)→{0, 1，2}。对于图 5中的相交部分，f₁(p)=1且f₂(p)=1，若取F(p)=1，则为图 5(a)；若取F(p)=2，则为图 5(b)；若按距离对F(p)进行取值，则为图 5(c)。

图  4  多标签网格剖分

Figure  4.  Multi-label Triangulation

下载: 全尺寸图片 幻灯片

图  5  中间域的几种处理方式

Figure  5.  Several Processing Ways of the Intermediate Material

下载: 全尺寸图片 幻灯片

3 算法分析和应用

CGAL(computational geometry algorithm library)是一种高效可靠的计算几何算法库，本文在CGAL网格剖分的基础上^[22]，通过修改多域多面体的预测构造方法，用于回答空间任一点是否在域内，以及属于哪一个子域，并分配相应子域的标签，实现了对多域多面体的表面重建，并将其应用于多域复杂矿体自适应网格剖分方法。

本文以北洺河铁矿多域矿体建模为例，采用所实现的多域自适应网格剖分方法来处理模型子域间存在大量交叉和空隙的问题。为了保持矿体的边界特征，在Delaunay细分前，将矿体建模轮廓线作为特征约束线进行初始特征采样保护。如图 6(a)所示，通过赋予轮廓线约束，可以构建完全与轮廓线相吻合的具有尖角等特征约束的网格模型。如图 6(b)所示，为了突出对某种子矿体的关注，通过对不同矿体类型分配不同的网格细分标准，可以获得在特定子域上的密集网格。

图  6  特征保护与自适应网格剖分

Figure  6.  Feature Protection and Adaptive Meshing

下载: 全尺寸图片 幻灯片

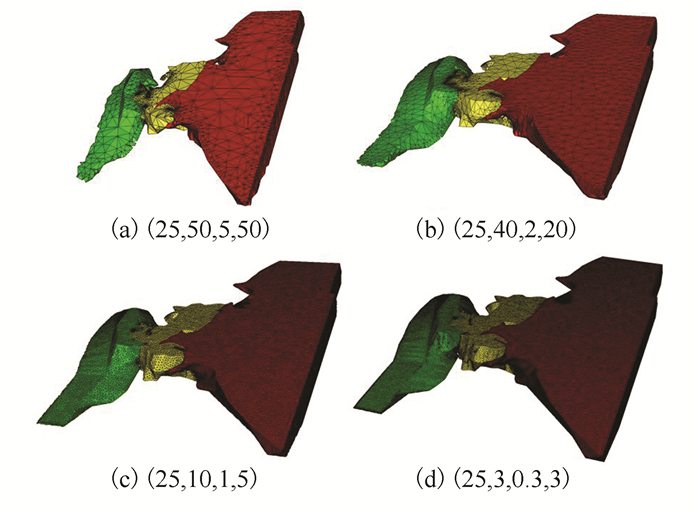
用于算法性能测试的运行环境为Windows64位的PC，处理器类型为Intel(R) Core(TM) i7-5820K CPU，时钟频率为3.30 GHz，具有16 GB RAM。选取§2.2所述不同的网格细分参数(α, l, d, L)，即边界面最小角度α、边界面最大边长l、边界面与三角面片之间的最大距离d，四面体最大边长L。不同细化标准下算法的计算性能如表 1所示，相应矿体剖分结果如图 7所示。

表  1  不同细化标准下算法的计算性能

Table  1.  Computational Performance of the Algorithm in Different Refinement Criteria

(α, l, d, L)	特征尺寸/m	顶点数	面片数	四面体数	细分耗时/s	优化耗时/s	总共耗时/s
(25, 50, 5, 50)	50	4 342	18 006	12 135	4.5	3.7	21.5
(25, 40, 2, 20)	20	7 990	30 914	26 871	7.9	6.6	25.7
(25, 10, 1, 5)	5	107 396	136 518	560 395	17.4	77.9	114.7
(25, 3, 0.3, 3)	3	479 823	478 580	2 698 969	59.8	78.8	149.5

下载: 导出CSV 

| 显示表格

图  7  不同细分标准下网格剖分结果

Figure  7.  Meshing Results in Different Refinement Criteria

下载: 全尺寸图片 幻灯片

对于相交部分域，可以通过修改标签的方法，将子标签分配给父标签进行域分离。以北洺河铁矿多域矿体建模为例，采用传统的显式建模方法容易产生复杂的交叉情况，造成模型的二义性；而采用本文的多域自适应网格剖分方法则可以保证子域模型之间良好的邻接特征，结果如图 8所示。多域矿体剖分不再相交，中间域被很好地分离开来，避免了复杂边界处的交叉情况。

图  8  多域矿体剖分结果

Figure  8.  Meshing Results of Multi-domain Orebodies

下载: 全尺寸图片 幻灯片

实际上, 该方法具有很大的灵活性，可以处理多种输入源的组合数据，比如隐式函数、三维灰度图、三维图像等，只需要构造一个预测方法，用于回答空间任一点是否在域内，以及如果在域内，则属于哪一个子域。

4 结语

本文在Delaunay细分算法的基础上，通过修改多域多面体的预测构造方法，对中间域进行分离或通过距离场对中间域进行拟合，应用Delaunay细分方法实现了一种适用于多域复杂矿体的网格剖分方法。

该方法既可以用于处理多种矿体建模存在的边界交叉问题，也可以用于处理多域自适应网格剖分问题。同时，通过对矿体轮廓线进行特征约束，可以获得与轮廓线完全吻合的网格剖分结果；通过定义统一或非均匀的自适应尺寸场，可以获得感兴趣区域的密集网格。基于Delaunay细分的多域网格剖分方法，除了可以生成无缝、连续的多域模型之外，通过网格优化还可以生成高质量的四面体和三角网格，避免轮廓线拼接法大量退化和奇异三角形的存在。

该方法在逆向工程、有限元分析、科学计算可视化等领域中也都具有重要的参考价值。今后需要进一步研究的内容包括：复杂边界特征自动检测与保护，对交叉介质和空隙介质的进一步参数化拟合以及算法性能的进一步提升等。