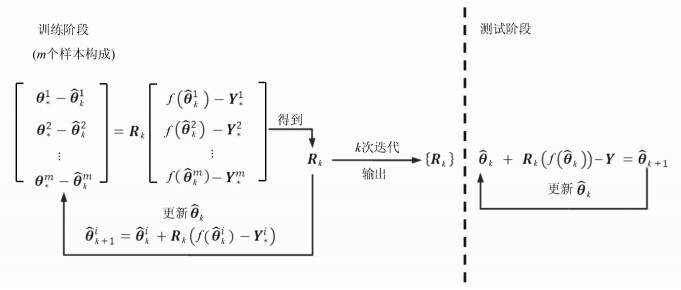
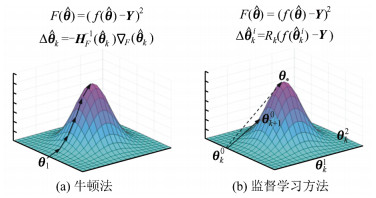
-
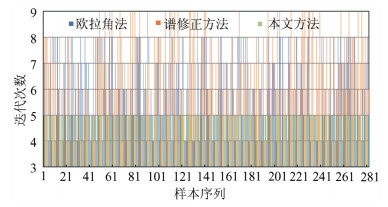
摘要: 单像空间后方交会可描述为非线性最小二乘问题,不可导、法方程系数矩阵病态以及陷入局部极值是造成其数值过程不收敛的主要原因。不同地区的控制点空间分布不具相似性,若把同一地区同一组控制点之下数张已知外方位元素的像片看作一个样本集,则在给定每个外方位元素初值的前提下,可通过监督学习方法求取外方位元素的整体下降方向;而对于单像空间后方交会中因前述原因不收敛的情况,则可采用整体下降方向近似解算。以此为出发点,提出一种单像空间后方交会求解的监督学习方法,主要过程是:①训练阶段,利用监督学习过程,对同一测区内不同姿态像片所组成的样本集进行整体外方位元素的求解,得到该测区外方位元素的整体下降方向集合;②测试阶段,对该测区的任意像片,给定外方位元素的初值,直接采用训练阶段得到的整体下降方向集合进行外方位元素的迭代求解。对比试验表明,该方法在数值过程收敛性与初值依赖性上均表现出较强的优势,并能克服欧拉角法因法方程系数矩阵病态而无法收敛的情况。Abstract: The space resection of single image can be described as a problem of non-linear least squares, and the non-derivative, ill-conditioned coefficient matrix of normal equation and local extremum are main reasons for non-convergence in its numerical procedure. The spatial distribution of control points in different regions is not similar. If we put down the multiple images and have known their exterior orientation elements regarding the same control points under the same region, as a sample set, the overall descent direction can be obtained by supervised learning under the circumstance that every initial values of exterior orientation elements have been given. What's more, in the case of non-convergence in original space resection of single image because of the reasons mentioned before, it can be approximately solved by using the overall descent direction. From this angle, a supervised learning method for solving space resection of single im age is proposed. The process mainly includes:①Training stage, in which supervised learning process is utilized and the descend direction set of exterior orientation elements is obtained by solving the overall exterior orientation elements of images set with different attitude in the same survey area. ②Testing stage, in which for any image in study area, the exterior orientation elements can be calculated iteratively if the initial value and the descend direction set were given from the process of supervised training. Experimental results show that the method in this paper is more efficient in numerical procedure convergence and dependence of the initial value than the current there realized. Besides, it can overcome the non-convergence of Euler angles caused by the ill-conditioned coefficient matrix of normal equation, which is essentially the gradient matrix.
-
遥感变化检测是利用不同时相的遥感影像和相关地理数据,结合遥感成像机理和地物特性,采用图像、图形处理理论和数学模型方法,确定和分析研究区的地表覆盖变化范围和变化类型。其研究目的是提取研究区变化信息,并生成变化图[1-2]。
高分辨率遥感影像比中低分辨率遥感影像具备更加丰富的光谱、纹理和形状等地物特征,但影像中同类地物的差异性增强,不同地物的光谱特征相互混淆,影像光谱域的统计可分性降低,信息提取难度增大,影像中“同物异谱,异物同谱”的现象大量发生,加重了地物光谱和纹理特征的离散程度,使得基于像元的变化检测精度难以提高[3]。
深度学习[4-5]作为机器学习的一个重要分支,可以自动地将简单特征组合成复杂特征,并利用复杂特征进行分类,分类精度大大提高,其在变化检测领域的应用比其他方法更为宽泛,适用性也更强。随着AlexNet[6]、VGG[7]、GoogLeNet[8]和ResNet[9-10]等深度学习网络的出现,神经网络在变化检测领域得到了成功应用。张鑫龙等[2]提出了基于深度玻尔兹曼机的深度学习变化检测方法;Peng等[10]提出了一种改进的用于语义分割编码器-解码器结构,端到端变化检测方法;Mou等[11]将光谱空间模块和时态模块进行组合,设计了一种循环3D全卷积网络用于建筑物变化检测。虽然国内外学者针对变化检测中存在的问题进行了大量研究,但深度学习变化检测方法优质训练样本的选取和自动化程度、基于像元检测的“椒盐”现象和伪变化区的出现等仍是目前亟待解决的问题[12-14]。
领域知识在遥感影像变化检测中的应用,对于解决图像处理算法的局限性、提高变化检测的精度和图像处理的自动化程度具有较为理想的效果[3]。深度置信网络(deep belief networks,DBN)是深度学习领域较为经典的模型,它通过联合概率分布来推断样本数据分布,非常适用于基于像元的变化检测研究。改进的变化矢量分析算法[2](robust change vector analysis,RCVA)和灰度共生矩阵算法[15-16](grey level co-occurrence matrix,GLCM)能够提取影像光谱和纹理差异特征,减小由于预处理阶段的配准所造成的误差,减弱高分辨率遥感影像中地物间光谱特征相互混淆等不利因素对检测结果的影响。
本文以DBN为深度学习模型,利用RCVA和GLCM算法提取影像光谱和纹理差异特征。将原理性和经验性的领域知识整合成为知识规则,用于选取优质训练样本并作为优化深度学习变化检测结果的依据。通过高分二号与IKONOS影像的变化检测实验,验证了本文方法的有效性。
1 本文方法
1.1 光谱变化特征提取
由于不同时相影像成像条件不同,在对影像进行精配准后,影像间的配准误差仍难以消除。其结果则是两幅影像间的像元对应关系不正确,进而导致了检测时伪变化区的大量出现。RCVA算法通过考虑像元的邻域信息,选择光谱差异最小的像元对进行检测,消除了配准误差带来的影响。
RCVA算法原理如下:基于影像1中的某个像元
,在影像2 范围内求与 亮度值差异最小的像元 ,此时认为 为 的同名像点,并求取差值 ,表示通过亮度值求得的影像1中 点的变化强度值。同样,基于影像2求对应影像1中的同名像点,并求取差值 ,表示通过亮度值求得的影像2中 点的变化强度值,以 和 较小者作为该点变化强度。 遍历影像,可得到所有像元的光谱变化强度值,进而得到考虑邻域信息的光谱变化强度图。
1.2 纹理变化特征提取
纹理特征是反映图像中同质的一种视觉特征,它体现了物体表面的结构组织排列属性,对于反映物体的表层特征变化具有重要利用价值。GLCM是提取纹理的一种经典方法,也是目前普遍使用且提取效果较好的纹理特征分析法[16]。已有的研究定义了14种标量来进行纹理分析,其中最常用的有均值、方差、协同性、对比度、熵等8 种。以方差为标量研究纹理特征时,最能反应不同地物间的差异[17-18]。
得到两幅影像的方差特征值后,即可通过差值计算得到纹理变化强度图。
1.3 结合领域知识的训练样本优化
根据光谱变化和纹理变化强度图,通过设置不同阈值提取样本,可对样本进行不同程度的划分。为保证样本的充分性,最大限度地选择到具有代表性的变化地物和未变化地物样本,通过自定义阈值取并集的方式,分析得出合理的阈值组合,并选择该阈值组合下的标记样本作为待优化样本。
阈值组合的选取如下:以光谱变化和纹理变化强度图为基准,在最小强度值和最大强度值闭区间内,从小到大逐个设置阈值对样本进行标记;以参考变化结果为依据,对所有阈值下的样本标记结果进行统计,计算其准确率;计算相邻阈值间的准确率增幅,由于准确率反映了正负样本标记的正确程度,因此在准确率增幅趋于稳定前的节点处即可选定较为合理的阈值;以相同的方法分别获得RCVA和GLCM下的合理阈值,即组成阈值组合。通过变化强度区间逐个分析得到合理阈值的方式,对阈值的分析较细致,同样能够运用于其他情景下的阈值分析。
高分辨率遥感影像中异常光谱值多,同时,由于影像获取时间和获取条件的不同,植被季节性返青和建筑物阴影区等因素影响,造成了伪变化样本的大量出现。
1)形状特征知识。本文结合领域知识,引入面积(S)和形状复杂度(C)两种形状特征指数作为过滤离散伪变化样本的优化策略。优化策略定义为:(1)
,即所有变化样本组成的图斑,其面积均应大于等于最小定义图斑面积,若不满足,则将其归并为未变化样本;(2) , 为待检测图斑周长, 为其面积,当满足条件 时, 值越大说明图斑越复杂,是离散碎图斑的概率就越大,可将其归并为未变化样本。根据形状特征知识,本文设计的各类小图斑检测图谱如图 1所示。 图 1中共有134种图斑类型,是像素个数不大于4的所有图斑形式,其中,(a)~(l)为根据图斑形状和遍历窗口大小进行的排序。将待检测图斑与图 1比对,若形状相同,则可对该图斑进行删除或归并(归为未变化图斑)。
2)光谱特征知识。针对植被(农作物、绿化带等)季节性返青和建筑物阴影等因素所引起的带状、块状伪变化样本集中区,通过对两幅影像固定窗口内同名像元亮度值采样的方式,自定义光谱映射区间。依据光谱映射区间建立光谱知识规则,并对两幅影像进行遍历,剔除伪变化样本。
映射关系建立方式为:
式中,
和 分别为两幅影像中同名像元红、绿、蓝3个波段的亮度值 ; 与 为映射区间下限; 与 为映射区间上限; 为滑动窗口大小。 1.4 DBN模型训练与变化检测
DBN是一种概率生成模型[19],通过联合概率分布来推断样本数据分布。通过逐层非监督的训练方式对大量无标签样本数据进行特征提取,并通过少量有标签的样本数据进行模型优化,最后获得网络最优权重,使得网络能依据最大概率生成训练数据。DBN主要由两部分构成,第一是多层限制玻尔兹曼机(restricted Boltzmann machine,RBM),用于预训练网络;第二是前馈反向传播网络,此部分可以使RBM堆叠的网络更加精细化。
RBM含有两层(显层
、隐层 ),为无向图模型,每层可定义为一个向量,向量的维度即为该层神经元的个数,不同层之间的神经元由权值矩阵 连接。对于每一个RBM,都有其作为一个系统所具备的能量,而根据能量函数则可以得到关于 与 的联合概率分布 ( 为模型参数, 为神经元 、 之间的权重, 和 分别表示显层和隐层神经元间的偏置),DBN则是通过基于 的相关计算来重构样本数据。经过迭代可不断优化网络参数,达到初始化每个RBM参数的目的。当RBM网络中的特征向量在映射到不同特征空间时能够保存最多的特征信息,完成DBN的预训练。基于误差反向传播算法,利用有标签的样本数据,通过计算各RBM层的学习误差,对网络权值 进行更新,微调整个模型,完成DBN的训练。 RBM的显层用来接收变量,且传统的输入多为二值变量,而连续输入的实值变量则更适用于图像分类和语音识别等[2]。本文DBN的输入为2×2像素范围内像元红、绿、蓝3波段的归一化亮度值依次排列的向量。
利用预选好的样本对模型进行训练,当训练精度达到精度要求后,对模型进行保存,并利用模型对整幅影像进行检测,得到变化检测结果。由于DBN模型是基于像元的变化检测,模型训练完毕后权值已固化,因此当进行变化检测时会出现少量的“椒盐”噪点。为进一步提高检测精度,利用图 1中的(a)检测图斑对未变化区域中的孤立点进行剔除,对变化区域中的孤立点进行填充,得到最终的变化检测结果。
2 实验与分析
2.1 实验1
实验1所用数据为2016-05-19和2017-04-29获取的长春市某地区高分二号遥感影像,影像分辨率为1 m,包含红、绿、蓝3个波段,影像大小为1 389×2 200像素,如图 2(a)所示;利用RCVA和GLCM得到变化强度图如图 2(b)所示。通过分析准确率增幅,选定RCVA和GLCM的阈值分别为75和16,作为划分变化样本的尺度。准确率增幅随阈值变化趋势图如图 3所示。在该阈值组合下得到的变化样本,覆盖范围较广,各类变化地物样本标记较全面、充分,变化样本标记情况如图 4(a)所示。
利用领域知识优化策略,对所标记的变化样本进行过滤,得到能够准确反映变化与未变化区域的高质量样本。对植被季节性返青区和建筑物阴影区的典型区域进行采样,建立映射区间,剔除伪变化区。执行优化策略后的变化样本标记图如图 4(b)所示,其中,红色实线框内为建筑物阴影被大量剔除的典型区域,红色虚线框内为植被季节性返青大量剔除的典型区域。与图 4(a)对比可知,执行优化策略后有大量伪变化样本被剔除。
根据图 4(b)的样本标记图,共选取变化样本211 637个,未变化样本2 844 163个。为了验证本文方法的有效性,分别在已有的变化与未变化样本中随机选取了不同数量的样本对DBN进行训练,并统计了DBN变化检测结果的准确率、召回率、虚警率和漏检率,如表 1所示,其中,A、B、C分别代表训练样本优化前、训练样本优化后和变化检测结果优化后。
表 1 训练样本优化前后精度分析表(实验1)Table 1. Precision Analysis Before and After Optimizing Training Samples (Experiment 1)数量/个 准确率/% 召回率/% 虚警率/% 漏检率/% 正样本 负样本 A B C A B C A B C A B C 5 000 5 000 88.70 93.28 93.77 65.30 76.30 80.10 60.42 42.42 39.76 34.70 23.70 19.90 10 000 10 000 88.63 94.09 94.59 66.59 73.75 78.68 60.45 37.37 34.30 33.41 26.25 21.32 30 000 30 000 88.26 92.45 93.07 66.60 78.95 83.68 61.46 46.57 43.70 33.40 21.05 16.32 50 000 50 000 87.72 91.74 92.80 68.21 79.16 83.45 62.62 49.44 44.96 31.79 20.84 16.55 80 000 80 000 86.90 94.42 94.48 69.14 73.14 75.21 64.37 35.09 34.15 30.86 26.86 24.79 由表 1可知,训练样本优化后,准确率和召回率有较大幅度提高,其中,准确率最大增幅7.52%,召回率最大增幅12.35%;虚警率和漏检率有较大幅度下降,其中,虚警率最大降幅29.28%,漏检率最大降幅12.35%。对变化检测结果优化后,准确率最大增幅1.06%,召回率最大增幅4.93%,虚警率最大降幅4.48%,漏检率最大降幅4.93%。
参考变化以及变化检测结果如图 5所示。其中,参考变化结果为遥感图像解译人员通过目视解译获得,并在实地进行了调绘。通过实地调绘结果的对比与补充,参考变化结果与实地变化情况符合度较高(精度优于95%)。与参考变化结果对比,可明显看出,训练样本优化后,DBN的检测准确性显著提高,大量伪变化区域被剔除,变化与未变化区域能够被正确识别。
2.2 实验2
实验2数据选自在武汉多时相场景变化检测数据集(multi-temporal scene Wuhan,MtS-WH),影像由IKONOS传感器分别获取于2002-02-11和2009-06-24,分辨率为1 m,包含红、绿、蓝和近红外4个波段,实验区影像大小为1 778×1 784像素。实验区影像及RCVA、GLCM变化强度图如图 6所示,选定的RCVA和GLCM的阈值分别为79和28。优化前后变化样本标记图如图 7所示,其中红色实线框内为建筑物阴影被大量剔除的典型区域,红色虚线椭圆形内为植被季节性返青大量剔除的典型区域。
参考变化检测结果是通过MtS-WH中给出的类别标签作差,附加人工目视解译得到,类别标签作差过程完全按照MtS-WH的类别参考结果进行,可认为无相对误差,参考变化及变化检测结果如图 8所示。不同数量训练样本得到的DBN变化检测的精度如表 2所示。
表 2 训练样本优化前后精度分析表(实验2)Table 2. Precision Analysis Before and After Optimizing Training Samples (Experiment 2)数量/个 准确率/% 召回率/% 虚警率/% 漏检率/% 正样本 负样本 A B C A B C A B C A B C 5 000 5 000 73.27 83.57 86.29 64.58 73.37 77.79 45.42 27.75 23.23 35.42 26.63 22.21 10 000 10 000 72.20 83.83 85.70 66.89 77.86 79.02 47.13 28.99 25.26 33.11 22.14 20.98 30 000 30 000 72.28 84.37 86.97 57.26 79.39 81.13 46.57 28.42 23.27 42.74 20.61 18.87 50 000 50 000 73.83 83.93 86.52 65.20 80.86 82.28 44.60 29.88 24.87 34.80 19.14 17.72 80 000 80 000 72.95 84.51 87.46 63.06 81.81 84.87 45.80 29.04 23.83 36.94 18.19 15.13 由表 2可知,实验2准确率和召回率都有较大幅度的提高,其中,准确率最大增幅为12.14%,召回率最大增幅为22.13%;同时,虚警率和漏检率都有较大幅度的下降,虚警率最大降幅为18.15%,漏检率最大降幅为22.13%。变化检测结果优化后,准确率最大增幅为2.95%,召回率最大增幅为4.42%,虚警率最大降幅为5.12%,漏检率最大降幅为4.42%。
3 结语
本文提出一种利用领域知识优化策略进行高分辨率遥感影像深度学习变化检测的方法。根据RCVA和GLCM提取的光谱和纹理特征标定初选样本;利用领域知识优化策略对样本进行筛选,获得优质样本;训练DBN模型,得到变化检测结果,并利用优化策略对检测结果进行优化。实验表明,本文方法能够有效提高变化检测结果的准确率和召回率,大幅度降低虚警率和漏检率。通过提高训练样本质量,进而提高深度学习模型检测性能,为高分辨率遥感影像深度学习变化检测提供了一条新途径。同时,在变化检测结果的基础上执行优化策略,则进一步提高了检测结果的精度。
-
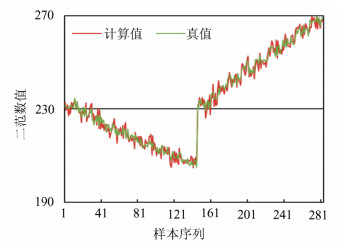
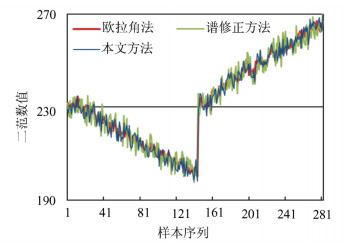
表 1 理想垂直摄影外方位元素计算结果
Table 1 Result of Calculation of Ideal Vertical Photography
元素 项目 真值 欧拉角法 监督学习方法 线元素/m XS 0.000 000 不收敛 0.001 565 YS 0.000 000 -0.002 479 ZS 150.000 000 150.003 025 角元素/rad φ 0.000 000 不收敛 0.000 009 ω 0.000 000 -0.000 002 κ 0.000 000 0.000 012 表 2 地面控制点坐标
Table 2 Coordinates of GCPs
点号 X/m Y/m Z/m 1 10 10 11 2 160 40 24 3 320 40 34 4 10 160 11 5(A) 160 160 0 6 320 160 28 7 40 320 14 8 160 320 29 9 320 320 27 -
[1] 张祖勋, 张剑清.数字摄影测量学[M].武汉:武汉大学出版社, 1996 Zhang Zuxun, Zhang Jianqing. Digital Photogrammetry[M]. Wuhan:Wuhan University Press, 1996
[2] 王之卓.摄影测量原理[M].武汉:武汉大学出版社, 2007 Wang Zhizhuo. The Principles of Photogrammetry[M]. Wuhan:Wuhan University Press, 2007
[3] 袁修孝.航空摄影测量影像定向的若干探讨[J].地球科学进展, 2007, 22(8):828-834 doi: 10.3321/j.issn:1001-8166.2007.08.008 Yuan Xiuxiao. Some Investigations of Image Orientation in Aerial Photogrammetry[J]. Advances in Earth Science, 2007, 22(8):828-834 doi: 10.3321/j.issn:1001-8166.2007.08.008
[4] 唐利民.非线性最小二乘的不适定性及算法研究[D].长沙: 中南大学, 2011 http://cdmd.cnki.com.cn/Article/CDMD-10533-1011177506.htm Tang Limin. Research on the Ill-posed and Solving Methods of Nonlinear Least Squares Problem[D]. Changsha: Central South University, 2011 http://cdmd.cnki.com.cn/Article/CDMD-10533-1011177506.htm
[5] Haralick B M, Lee C N, Ottenberg K, et al. Review and Analysis of Solutions of the Three Point Perspective Pose Estimation Problem[J]. International Journal of Computer Vision, 1994, 13(3):331-356 doi: 10.1007/BF02028352
[6] 冯文灏.近景摄影测量[M].武汉:武汉大学出版社, 2002 Feng Wenhao. Close Range Photogrammetry[M]. Wuhan:Wuhan University Press, 2002
[7] 付仲良, 周凡, 俞志强.综合多种特征的后方交会法[J].测绘学报, 2014, 43(8):827-834 http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201408009.htm Fu Zhongliang, Zhou Fan, Yu Zhiqiang. A Space Resection Synthesized the Multiple Features[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8):827-834 http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201408009.htm
[8] 李斐, 郝卫峰, 王文睿, 等.非线性病态问题解算的扰动分析[J].测绘学报, 2011, 40(1):5-9 http://d.old.wanfangdata.com.cn/Periodical/chxb201101002 Li Fei, Hao Weifeng, Wang Wenrui, et al. The Perturbation Analysis of Nonlinear Ill-conditioned Solution[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1):5-9 http://d.old.wanfangdata.com.cn/Periodical/chxb201101002
[9] 郭忠磊, 翟京生, 邓凯亮.基于LM方法的大姿态角影像空间后方交会[J].武汉大学学报·信息科学版, 2016, 41(4):565-568 http://ch.whu.edu.cn/CN/abstract/abstract5432.shtml Guo Zhonglei, Zhai Jingsheng, Deng Kailiang. Space Resection of Big Attitude Image Based on Levenberg-Marquardt Method[J]. Geomatics and Information Science of Wuhan University, 2016, 41(4):565-568 http://ch.whu.edu.cn/CN/abstract/abstract5432.shtml
[10] 何敬, 李永树.基于特征点和最优路径的无人机影像拼接方法[J].遥感技术与应用, 2012, 27(2):173-219 http://d.old.wanfangdata.com.cn/Periodical/ygjsyyy201202003 He Jing, Li Yongshu. A Mosaic Method in Unmanned Aerial Vehicle Images Based on Feature Points and Optimal Path[J]. Remote Sensing Technology and Application, 2012, 27(2):173-219 http://d.old.wanfangdata.com.cn/Periodical/ygjsyyy201202003
[11] Ji Q, Costa M S, Haralick R M, et al. A Robust Linear Least-Squares Estimation of Camera Exterior Orientation Using Multiple Geometric Features[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2000, 55(2):75-93 doi: 10.1016/S0924-2716(00)00009-5
[12] 官云兰, 程效军, 周世健, 等.基于单位四元数的空间后方交会解算[J].测绘学报, 2008, 37(1):30-35 doi: 10.3321/j.issn:1001-1595.2008.01.006 Guan Yunlan, Cheng Xiaojun, Zhou Shijian, et al. A Solution to Space Resection Based on Unit Quaternion[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1):30-35 doi: 10.3321/j.issn:1001-1595.2008.01.006
[13] Lepetit V, Moreno-Noguer F, Fua P. EPnP:An Accurate O(n)Solution to the PnP Problem[J]. International Journal of Computer Vision, 2009, 81(2):155-166 doi: 10.1007/s11263-008-0152-6
[14] Penatesanchez A, Andradecetto J, Morenonoguer F. Exhaustive Linearization for Robust Camera Pose and Focal Length Estimation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(10):2387-2400 doi: 10.1109/TPAMI.2013.36
[15] 龚辉, 姜挺, 江刚武, 等.一种基于四元数的空间后方交会全局收敛算法[J].测绘学报, 2011, 40(5):639-645 http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201105020.htm Gong Hui, Jiang Ting, Jiang Gangwu, et al. A Globally Convergent Algorithm of Space Resection Based on Quaternion[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5):639-645 http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201105020.htm
[16] 江刚武, 姜挺, 王勇, 等.基于单位四元数的无初值依赖空间后方交会[J].测绘学报, 2007, 36(2):169-175 doi: 10.3321/j.issn:1001-1595.2007.02.010 Jiang Gangwu, Jiang Ting, Wang Yong, et al. Space Resection Indepentent of Initial Value Based on Unit Quaternions[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2):169-175 doi: 10.3321/j.issn:1001-1595.2007.02.010
[17] 张永军, 吴磊, 林立文, 等.摄影测量中病态问题的条件数指标分析[J].武汉大学学报·信息科学版, 2010, 35(3):308-312 http://ch.whu.edu.cn/CN/abstract/abstract882.shtml Zhang Yongjun, Wu Lei, Lin Liwen, et al. Condition Numbers for Evaluation of Ill-posed Problems in Photogrammetry[J]. Geomatics and Information Science of Wuhan University, 2010, 35(3):308-312 http://ch.whu.edu.cn/CN/abstract/abstract882.shtml
[18] 王海亮, 向茂生, 李杨, 等.两种单像空间后方交会模型分析[J].光学技术, 2010, 36(1):14-19 http://d.old.wanfangdata.com.cn/Periodical/gxjs201001004 Wang Hailiang, Xiang Maosheng, Li Yang, et al. The Analysis of Two Single Image Space Resection Models[J]. Optical Technique, 2010, 36(1):14-19 http://d.old.wanfangdata.com.cn/Periodical/gxjs201001004
[19] 王振杰.测量中不适定问题的正则化解法[M].北京:科学出版社, 2006 Wang Zhenjie. Regularization of Ill-posed Problems in Surverying[M]. Beijing:Science Press, 2006
[20] 葛旭明, 伍吉仓.病态总体最小二乘问题的广义正则化[J].测绘学报, 2012, 41(3):372-377 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=chxb201203011 Ge Xuming, Wu Jicang. Generalized Regularization to Ill-posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3):372-377 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=chxb201203011
[21] 欧吉坤.测量平差中不适定问题的统一表达和选权拟合法[J].测绘学报, 2004, 33(4):283-288 doi: 10.3321/j.issn:1001-1595.2004.04.001 Ou Jikun. Uniform Expression of Solutions of Illposed Problems in Surveying Adjustment and the Fitting Method by Selection of the Parameter Weights[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(4):283-288 doi: 10.3321/j.issn:1001-1595.2004.04.001
[22] 蒋涛, 李建成, 王正涛, 等.航空重力向下延拓病态问题求解[J].测绘学报, 2011, 40(6):684-689 http://cdmd.cnki.com.cn/Article/CDMD-10732-1014421889.htm Jiang Tao, Li Jiancheng, Wang Zhengtao, et al. Solution of Ill-posed Problem in Downward Continuation of Airborne Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6):684-689 http://cdmd.cnki.com.cn/Article/CDMD-10732-1014421889.htm
[23] 闫利, 聂前, 赵展.利用单位四元数描述线阵CCD影像的空间后方交会[J].武汉大学学报·信息科学版, 2010, 35(2):201-204 http://ch.whu.edu.cn/CN/abstract/abstract846.shtml Yan Li, Nie Qian, Zhao Zhan. Space Resection of Line Scanner CCD Image Based on the Description of Quaternions[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2):201-204 http://ch.whu.edu.cn/CN/abstract/abstract846.shtml
[24] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M]. 2版.武汉:武汉大学出版社, 2009 The Subject Group of Surveying Adjustment of Institute of Surveying and Mapping of Wuhan University. Error Theory and Fundation of Surveying Adjustment[M]. 2nd ed. Wuhan:Wuhan University Press, 2009
[25] 席少霖.非线性最优化方法[M].北京:高等教育出版社, 1992 Xi Shaolin. The Method of Nonlinear Optimization[M]. Beijing:Higher Education Press, 1992
[26] 张剑清, 潘励, 王树根.摄影测量学原理[M]. 2版.武汉:武汉大学出版社, 2009 Zhang Jianqing, Pan Li, Wang Shugen. The Principles of Photogrammetry[M]. 2nd ed. Wuhan:Wuhan University Press, 2009
-
期刊类型引用(7)
1. 刘立,董先敏,王德富,张志强,刘娟. 人机协同的多模态遥感变化检测方法. 测绘通报. 2024(S1): 130-136 .  百度学术
百度学术
2. 刘莺迎,周刚. 基于孪生Transformer的双时相遥感影像变化检测方法. 遥感信息. 2024(03): 67-74 .  百度学术
百度学术
3. 张永军,王飞,李彦胜,欧阳松,魏东,刘晓建,孔德宇,CHEN Ruixian,ZHANG Bin. 遥感知识图谱创建及其典型场景应用技术. 遥感学报. 2023(02): 249-266 .  百度学术
百度学术
4. 周豫阳,王明常,王凤艳,杨盈,刘子维. 改进U-Net的高分辨率遥感影像建筑区变化检测方法. 世界地质. 2023(01): 159-167 .  百度学术
百度学术
5. 陈桥驿,闫宇飞,黄永芳. 融合面向对象和深度置信网络的农村建筑物信息提取. 测绘通报. 2023(06): 134-137 .  百度学术
百度学术
6. 张征稳. 面向建筑物边缘特征保持的遥感影像变化检测研究. 测绘与空间地理信息. 2023(S1): 203-207 .  百度学术
百度学术
7. 梁宇,左栋. “问题地图”智能检测发展现状与关键技术. 测绘通报. 2023(10): 111-116 .  百度学术
百度学术
其他类型引用(4)






 下载:
下载: