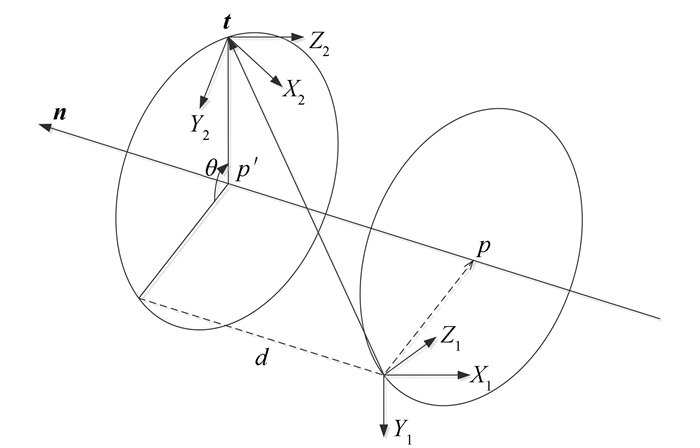
A Linear Features-Constrained, Plücker Coordinates-Based, Closed-Form Registration Approach to Terrestrial LiDAR Point Clouds
-
摘要: 经典的基于点状特征匹配的地面激光雷达（light detection and ranging，LiDAR）点云配准算法实现过程中，点状特征的提取精度对算法运行结果的影响通常较大；基于迭代运算的LiDAR点云配准算法计算量大，对未知参数的初值依赖程度较高，在求解大转角刚体变换参数时算法不稳定。对此，提出了一种线状特征约束下基于Plücker直线坐标描述的LiDAR点云配准算法。立足于经典的向量代数与对偶四元数的相关理论与方法，分析并确定了Plücker直线坐标与对偶四元数之间的相互转换关系以及模型描述方法；以LiDAR点云配准前后同名线状特征的Plücker直线坐标相等为约束条件，构建了线状特征约束下基于Plücker直线坐标描述的刚体变换模型；立足于最小二乘基本准则，通过目标函数的极值化分析实现了线状特征约束下地面LiDAR点云配准参数的直接求解。实验结果表明，所构建的基于Plücker直线坐标描述的地面LiDAR点云配准模型，无需事先确定变换参数的初值，避免了多元函数的线性化过程，解除了参数结果对于迭代初值的依赖，理论上克服了迭代法在求解大转角相似变换参数时的算法不稳定问题。此外，较之单纯基于点状特征匹配的LiDAR点云配准算法，该算法可以有效地增强LiDAR点云配准过程的约束，达到提高配准质量的目的。
-
关键词:
- 配准 /
- 刚体变换 /
- Plücker直线坐标 /
- 对偶四元数 /
- 直线特征约束
Abstract: Considering that the low accuracy of extracted point features may affect the seamless fusion of point clouds from two neighbor stations, and by using traditional iterative-form solutions to implement point clouds registration, the large amount of computer resources, the high dependence on initial values of unknown parameters, and its theoretical instability in solving transformation parameters for large-angle registration can hardly be neglected. To alleviate the above problems, a linear features-based, closed-form solution to registration of pairwise terrestrial LiDAR point clouds is proposed, in which Plücker coordinates is introduced to represent linear features in 3D space. A Plücker coordinate-based object function is first introduced on the assumption of the consistency of each conjugate linear features from the two neighbor stations after registration. Based on the theory of least squares and by extreme value analysis of the error norm, detailed derivations of the model and the main formulas are all given. Experiments show that the proposed algorithm is just the one expected, the linearization of multivariate function is neglected in the implementation, and it runs well without initial estimates of unknown parameters, which assures the stability in solving transformation parameters for large-angle registration problems. Furthermore, by employing linear features as registration primitives, random errors may be greatly decreased by fitting contrast to point features based registration algorithms. -
激光雷达(light detection and ranging，LiDAR)凭借其快速、高效、高精度等优良特性，为全面、真实、快速、准确地再现地理空间实体及其环境信息提供了可靠的数据保证。然而，地理实体的空间复杂度普遍较高，而LiDAR传感器的视觉面通常较窄，为了获取能够全面表征地理实体及其周边地物的表面特征数据，基于地面LiDAR技术的空间三维数据采集方法通常需要沿着多个不同的视向瞄准对象，采集目标地理实体及其周边地物的表面特征数据，并基于点云配准算法将原本各自独立的测站拼接到一起，以实现对地理实体及其周边环境信息的全面表达。
LiDAR点云配准的实质是寻求并确立相邻测站点云之间的特征对应关系，基于刚体变换模型对相邻测站坐标基准间的相对位置关系进行描述，解算用于描述两坐标基准间相对位置关系的旋转与平移参数，进而实现不同测站坐标系之间的相互转换与坐标基准的统一描述与表达。当前，LiDAR点云配准模型的常用解法是把刚体变换公式采用多元函数的泰勒公式展开，对其实施线性化处理，利用迭代的方式来实现变换参数的求解。但是，迭代法自身存在如下不足：(1)需要事先确定变换参数的初值，并据此实现非线性变换模型的线性化，初值选择不当，则可能会造成结果的不收敛；(2)受线性化过程的约束，此类方法本质上仅适用于小转角坐标变换的情况，在诸如摄影测量的绝对定向、LiDAR点云的配准等方面，若不能提供两坐标系统之间的近似变换参数，或提供的变换参数不够理想，计算结果的可靠性将受到严重影响。相比较而言，解析法通过最优化误差函数来计算得到刚体变换模型的参数，避免了初值计算以及由此带来的迭代不收敛问题，因此，研究LiDAR点云配准的解析求解算法具有重要的意义。
根据点云配准过程中旋转变换表达方法的不同，可将现有的LiDAR点云配准的解析求解算法分为3类：(1)利用向量代数来实现旋转变换过程的描述，并基于旋转矩阵的正交化和奇异值分解(single value decomposition，SVD)来实现变换参数的直接求解方法[1-2]；(2)基于单位四元数来实现旋转变换过程的描述，并基于此实现变换参数的直接求解方法[3-4]；(3)基于对偶四元数(dual quaternion，DQ)来实现旋转变换过程的描述，并基于此实现变换参数的直接求解方法[5-9]。其中，单位四元数仅利用4个参数即可实现旋转变换操作的简洁描述，较之旋转变换的向量代数(旋转矩阵)表示法，计算更为简单。然而，在求解刚体变换参数的过程中，平移向量的计算是建立在旋转变换参数结果的基础之上的，因此，结果的准确性在一定程度上将受到旋转变换参数的影响，且这种影响存在误差传递和累积现象。相比较之下，对偶四元数可实现旋转与平移参数的直接描述，旋转与平移参数求解过程之间不存在任何相关性，因此，近年来有关其在LiDAR点云配准及其相关应用中的研究受到密切关注。根据配准过程中配准基元选择的不同，可将现有的LiDAR点云配准算法区分为基于点状特征匹配的LiDAR点云配准[1-9]、基于线状特征匹配的LiDAR点云配准[10-15]、基于面状特征匹配的LiDAR点云配准[16]以及基于点、线、面共同约束的LiDAR点云配准[17]。分析可知，受LiDAR采样分辨率的影响，一般而言，线状特征与面状特征的提取精度应高于点状特征，其应用于LiDAR点云配准将有利于进一步提高配准的质量。然而，利用向量代数对三维空间中的直线特征进行描述[11]，其表达形式的多样性直接导致了基于线状特征约束的LiDAR点云配准算法模型构建的复杂性，这一现象在解析配准模型的设计中更为明显。Plücker直线坐标的提出为解决上述问题提供了可能，其通过直线方向向量与直线的矩等6个参数来对三维空间中的直线进行描述，几何意义明确，形式更加简洁。文献[16]基于Plücker直线坐标实现了相邻测站LiDAR点云的配准，基于对偶四元数实现了对于刚体变换的描述。然而，其算法的实现采用的是迭代法的基本思路，较之基于向量代数描述的迭代算法，虽然该算法对于迭代初值的选择依赖性较弱，但算法运行结果与初值选择之间的相关关系尚无法从理论上作出合理解释。
本文提出了一种线状特征约束下基于Plücker直线坐标描述的LiDAR点云配准算法。立足于经典的向量代数与对偶四元数的相关理论与方法，分析并确定了Plücker直线坐标与对偶四元数之间的相互转换关系以及模型描述方法；以LiDAR点云配准前后同名线状特征的Plücker直线坐标相等为约束条件，构建了线状特征下基于Plücker直线坐标描述的刚体变换模型；立足于最小二乘基本准则，通过目标函数的极值化分析实现线状特征约束下地面LiDAR点云配准参数的直接求解。通过上述研究，一方面，避免基于迭代的配准方法对于变换参数初值的依赖性；另一方面，克服LiDAR点云的点状特征提取精度不高以及基于单一的配准基元所带来的特征选择困难等问题，进而保证配准的质量。
1 利用Plücker坐标描述的LiDAR点云配准模型
1.1 对偶四元数与刚体变换
对偶四元数是由四元数和对偶数结合而来：
$$ \mathit{\boldsymbol{\hat q}} = \mathit{\boldsymbol{\dot r}} + \varepsilon \mathit{\boldsymbol{\dot s}} $$ (1) 式中，$\mathit{\boldsymbol{\dot r}}$和$\mathit{\boldsymbol{\dot s}}$都是四元数，分别为对偶四元数$\mathit{\boldsymbol{\hat q}}$的实部和对偶部；ε为$\mathit{\boldsymbol{\hat q}}$的对偶部单位。对偶四元数和纯四元数具有一个相似的表达形式：
$$ \mathit{\boldsymbol{\hat q}} = {\left[ {\begin{array}{*{20}{c}} {\cos \left( {\hat \theta /2} \right)}&{\sin \left( {\hat \theta /2} \right)\mathit{\boldsymbol{\hat n}}} \end{array}} \right]^{\rm{T}}} $$ (2) 式中，对偶向量$\mathit{\boldsymbol{\hat n}}$表示坐标系绕其旋转和平移的三维空间曲线；$\hat \theta $是旋转和平移的对偶角。
对偶向量$\mathit{\boldsymbol{\hat n}}$和对偶角$\hat \theta $的具体表达形式如下：
$$ \mathit{\boldsymbol{\hat n}} = \mathit{\boldsymbol{n}} + \varepsilon \left( {\mathit{\boldsymbol{p}} \times \mathit{\boldsymbol{n}}} \right) $$ (3) $$ \hat \theta = \theta + \varepsilon d $$ (4) 式中，n所表示的单位向量表示了旋转轴的方向和平移向量的方向；旋转是关于具有方向n并过点p(空间三维坐标p)的直线旋转了角度θ；d是沿着n所表示的方向上平移的距离。
不同坐标系统之间的空间相似变换由平移向量t、旋转轴n和旋转角θ来表示(尺度因子μ需要借助公共点坐标来确定，在此暂不予考虑)，首先依据t的方向和大小平移坐标系，其次关于n旋转角θ形成新的坐标系。基于四元数描述的空间相似变换可以取得同样的效果，其实现坐标变换的思路为：首先将原始坐标系沿着n的方向平移了距离d，关于具有单位向量n的直线旋转了角θ，n有方向并过点p。图 1详细表达了上述两种表示方法之间的区别与联系。
![]()
图 1 对偶四元数表示的旋转和平移Figure 1. Dual Quaternion Based Representation of Rotation and Translation将式(3)~(4)代入式(2)，化简得：
$$ \mathit{\boldsymbol{\dot r}} = {\left[ {\begin{array}{*{20}{c}} {\cos \left( {\theta /2} \right)}\\ {\sin \left( {\theta /2} \right)\mathit{\boldsymbol{n}}} \end{array}} \right]^{\rm{T}}} $$ (5) $$ \mathit{\boldsymbol{\dot s}} = {\left[ {\begin{array}{*{20}{c}} { - \left( {d/2} \right)\sin \left( {\theta /2} \right)}\\ {\left( {d/2} \right)\cos \left( {\theta /2} \right)\mathit{\boldsymbol{n}} + \sin \left( {\theta /2} \right)\left( {\mathit{\boldsymbol{p}} \times \mathit{\boldsymbol{n}}} \right)} \end{array}} \right]^{\rm{T}}} $$ (6) 如上所述，在不顾及缩放因子影响的情况下，表达不同坐标系之间的变换所需的独立变量数目为6(3个平移变量和3个旋转变量)，而一个对偶四元数包含8个元素。因此，唯一确定空间相似变换的参数需要附加相应的约束条件，综合式(2)~(6)，可以列出如下两个独立方程式作为附加约束条件：
$$ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{\dot r}} = 1\\ {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}} = 0 \end{array} \right. $$ (7) 1.2 基于Plücker坐标的空间直线表达
表达三维空间中的一条直线理论上需要6个参数：直线的方向向量l与直线所经过的点p的空间三维坐标p。然而，与空间中点的表达方式不同，经过一条直线的点可能有很多，因此，此种表示方法不具备唯一性。因此，当这种直线的表达方法应用于LiDAR点云配准模型的构建与表达时，会因此而影响配准模型构建的复杂性。
针对直线表达的唯一性问题，文献[18]提出了直线坐标的概念：对于空间中一条方向向量为l且过点p的直线，利用Plücker直线坐标可以表示为l、m，其中，m称之为直线的矩(line moment，LM)，其具体表达式为：m = p × l。
给定三维空间中的任意两点p1与p2，可以确定直线的方向向量l和直线的矩m (见图 2)：
$$ \left\{ \begin{array}{l} \mathit{\boldsymbol{l}} = {\mathit{\boldsymbol{p}}_2} - {\mathit{\boldsymbol{p}}_1}\\ \mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{p}}_1} \times {\mathit{\boldsymbol{p}}_2} \end{array} \right. $$ (8) ![]()
图 2 三维空间中基于Plücker坐标的直线表达Figure 2. Plücker-based Representation of a Line in 3D Space式中，p1与p2分别表示两个点的空间三维坐标；l是直线的方向向量; m是直线的矩，垂直于包含该直线且通过原点的平面。
如果在直线上取另外两个不同的点，根据线性坐标代换，可分别记为：
$$ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{p'}}}_1} = \lambda {\mathit{\boldsymbol{p}}_1} + \left( {1 - \lambda } \right){\mathit{\boldsymbol{p}}_2}\\ {{\mathit{\boldsymbol{p'}}}_2} = \mu {\mathit{\boldsymbol{p}}_1} + \left( {1 - \mu } \right){\mathit{\boldsymbol{p}}_2} \end{array} \right. $$ (9) 式中，λ和μ不相等。基于式(9)求得直线的方向向量l′和矩m′分别为：
$$ \left\{ \begin{array}{l} \mathit{\boldsymbol{l'}} = {{\mathit{\boldsymbol{p'}}}_2} - {{\mathit{\boldsymbol{p'}}}_1} = \left( {\lambda - \mu } \right)\mathit{\boldsymbol{l}}\\ \mathit{\boldsymbol{m'}} = {{\mathit{\boldsymbol{p'}}}_1} \times {{\mathit{\boldsymbol{p'}}}_2} = \left( {\lambda - \mu } \right)\mathit{\boldsymbol{m}} \end{array} \right. $$ (10) 可以看出，使用不同的端点确定的直线其方向向量与矩之间存在一个相同的缩放系数。
为了实现表达的唯一性，需要对直线的方向向量与直线的矩进行规则化处理，即将Plücker直线坐标的所有元素除以方向向量的模，结果称之为规则化Plücker直线坐标。根据式(8)与式(10)的关系可知：经规则化处理之后，任取一条直线上的两个特征点，其规则化Plücker直线坐标一致。总体来看，通过规则化Plücker直线坐标来对三维空间中的直线进行表达，几何意义明确，形式更加简洁，且‖ m ‖恰好等价于原点到达直线的垂直距离。更为重要的是，表达方式的唯一性为基于线状特征约束的LiDAR点云配准算法的模型构建提供了便利。
通常，规则化Plücker直线坐标可以由直线的方向向量与矩所构成的六元组Γ =[l m]来进行表达，或用对偶数的形式进行表达，即Γ = l +εm。需要注意的是, 对于一条直线，其方向向量与直线的矩满足正交关系，即l·m =0。
参照文献[3]中向量与单位四元数之间的转换关系，可按如下公式将归一化后的Plücker坐标扩展为8维：
$$ \mathit{\boldsymbol{ \boldsymbol{\hat \varGamma} }} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot l}}}&{\mathit{\boldsymbol{\dot m}}} \end{array}} \right] $$ (11) 其中，$\mathit{\boldsymbol{\dot l = }}\left[{{\bf{0}}\; \mathit{\boldsymbol{l}}} \right], \mathit{\boldsymbol{\dot m = }}\left[{{\bf{0}}\; \mathit{\boldsymbol{m}}} \right]$。
可以证明，式(11)满足对偶四元数的一切条件。因此，规则化Plücker直线坐标可以看作是满足特殊条件(l · m =0)的对偶四元数，即对偶四元数与直线的Plücker坐标可以直接进行运算。
1.3 基于对偶四元数描述的Plücker坐标变换
已知(la, ma)、(lb, mb)分别为三维空间中任意一条直线分别在两个不同坐标系中的方向向量与矩，三维空间中的直线变换可以表达为：
$$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{l}}_a} = \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{l}}_b}\\ {\mathit{\boldsymbol{m}}_a} = {\mathit{\boldsymbol{p}}_a} \times {\mathit{\boldsymbol{l}}_a} = \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{m}}_b} + \mathit{\boldsymbol{t}} \times \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{l}}_b} \end{array} \right. $$ (12) 根据单位四元数与三维空间中的旋转变换矩阵之间的对应关系，式(12)中的表达式la= R lb可以用单位四元数的形式表达为：
$$ {{\mathit{\boldsymbol{\dot l}}}_a} = \mathit{\boldsymbol{\dot r}}{{\mathit{\boldsymbol{\dot l}}}_b}{{\mathit{\boldsymbol{\dot r}}}^ * } $$ (13) 式中，${\mathit{\boldsymbol{\dot r}}}$表示与旋转矩阵R相对应的单位四元数；${\mathit{\boldsymbol{\dot r}}}$*表示单位四元数${\mathit{\boldsymbol{\dot r}}}$的共轭；${{\mathit{\boldsymbol{\dot l}}}_a}\mathit{\boldsymbol{ = }}\left[{0\; {\mathit{\boldsymbol{l}}_a}} \right], {{\mathit{\boldsymbol{\dot l}}}_b}\mathit{\boldsymbol{ = }}\left[{0\; {\mathit{\boldsymbol{l}}_b}} \right]$。
直线的矩ma= R mb+ t × R lb进一步表达为：
$$ {{\mathit{\boldsymbol{\dot m}}}_a} = \mathit{\boldsymbol{\dot r}}{{\mathit{\boldsymbol{\dot m}}}_b}{{\mathit{\boldsymbol{\dot r}}}^ * } + \frac{1}{2}\left( {\mathit{\boldsymbol{\dot t\dot r}}{{\mathit{\boldsymbol{\dot l}}}_b}{{\mathit{\boldsymbol{\dot r}}}^ * } + \mathit{\boldsymbol{\dot r}}{{\mathit{\boldsymbol{\dot l}}}_b}{{\mathit{\boldsymbol{\dot r}}}^ * }{{\mathit{\boldsymbol{\dot t}}}^ * }} \right) $$ (14) 式中，·表示四元数；*表示共轭。
令$\mathit{\boldsymbol{\dot s}} = \mathit{\boldsymbol{\dot t\dot r/}}{\rm{2}}$，式(14)可进一步改写为：
$$ {{\mathit{\boldsymbol{\dot m}}}_a} = \mathit{\boldsymbol{\dot s}}{{\mathit{\boldsymbol{\dot l}}}_b}{{\mathit{\boldsymbol{\dot r}}}^ * } + \mathit{\boldsymbol{\dot r}}{{\mathit{\boldsymbol{\dot m}}}_b}{{\mathit{\boldsymbol{\dot r}}}^ * } + \mathit{\boldsymbol{\dot r}}{{\mathit{\boldsymbol{\dot l}}}_b}{{\mathit{\boldsymbol{\dot s}}}^ * } $$ (15) 令$\mathit{\boldsymbol{\hat q = \dot r}} + \varepsilon \mathit{\boldsymbol{\dot s}}$，${{\mathit{\boldsymbol{ \boldsymbol{\hat \varGamma} }}}_a} = {{\mathit{\boldsymbol{\dot l}}}_a} + \varepsilon \left({{{\mathit{\boldsymbol{\dot m}}}_a}} \right)$，${{\mathit{\boldsymbol{ \boldsymbol{\hat \varGamma} }}}_b} = {{\mathit{\boldsymbol{\dot l}}}_b} + \varepsilon \left({{{\mathit{\boldsymbol{\dot m}}}_b}} \right)$，式(13)与式(15)可统一表达为：
$$ {{\mathit{\boldsymbol{ \boldsymbol{\hat \varGamma} }}}_a} = \mathit{\boldsymbol{\hat q}}{{\mathit{\boldsymbol{ \boldsymbol{\hat \varGamma} }}}_b}{{\mathit{\boldsymbol{\hat q}}}^ * } $$ (16) 其中，${\mathit{\boldsymbol{\hat q}}}$*表示对偶四元数${\mathit{\boldsymbol{\hat q}}}$的共轭，其具体表达形式为${{\mathit{\boldsymbol{\hat q}}}^\mathit{\boldsymbol{*}}}\mathit{\boldsymbol{ = }}{{\mathit{\boldsymbol{\dot r}}}^\mathit{\boldsymbol{*}}} + \varepsilon {{\mathit{\boldsymbol{\dot s}}}^\mathit{\boldsymbol{*}}}$。
至此，基于对偶四元数与Plücker直线坐标相互之间的运算，可以实现三维空间中直线的刚体变换。
利用矩阵对式(12)中的各项进行表达：
$$ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot l}}}_a} = \mathit{\boldsymbol{W}}{\left( {\mathit{\boldsymbol{\dot r}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right){{\mathit{\boldsymbol{\dot l}}}_b}\\ {{\mathit{\boldsymbol{\dot m}}}_a} = \mathit{\boldsymbol{W}}{\left( {\mathit{\boldsymbol{\dot r}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot s}}} \right){{\mathit{\boldsymbol{\dot l}}}_b} + \mathit{\boldsymbol{W}}{\left( {\mathit{\boldsymbol{\dot r}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right){{\mathit{\boldsymbol{\dot m}}}_b} + \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{W}}{\left( {\mathit{\boldsymbol{\dot s}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right){{\mathit{\boldsymbol{\dot l}}}_b} \end{array} \right. $$ (17) 式中，
$$ \mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right) = \left[ {\begin{array}{*{20}{c}} {{r_0}}&{ - {r_1}}&{ - {r_2}}&{ - {r_3}}\\ {{r_1}}&{{r_0}}&{ - {r_3}}&{{r_2}}\\ {{r_2}}&{{r_3}}&{{r_0}}&{ - {r_1}}\\ {{r_3}}&{ - {r_2}}&{{r_1}}&{{r_0}} \end{array}} \right] $$ $$ \mathit{\boldsymbol{W}}\left( {\mathit{\boldsymbol{\dot r}}} \right) = \left[ {\begin{array}{*{20}{c}} {{r_0}}&{ - {r_1}}&{ - {r_2}}&{ - {r_3}}\\ {{r_1}}&{{r_0}}&{{r_3}}&{ - {r_2}}\\ {{r_2}}&{ - {r_3}}&{{r_0}}&{{r_1}}\\ {{r_3}}&{{r_2}}&{ - {r_1}}&{{r_0}} \end{array}} \right] $$ 用矩阵对式(17)进行表达，可得：
$$ \left[ {{{\mathit{\boldsymbol{\dot l}}}_a}{{\mathit{\boldsymbol{\dot m}}}_a}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right)}&0\\ {\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot s}}} \right) + \mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot s}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right)}&{\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot l}}}_b}}\\ {{{\mathit{\boldsymbol{\dot m}}}_b}} \end{array}} \right] $$ (18) 考虑到误差的存在，并基于最小二乘准则，基于线状特征的LiDAR点云配准模型的实质是配准之后同名线状特征(la, ma)与(lb, mb)之间的差值平方和达到最小。
令：
$$ {\mathit{\boldsymbol{f}}_1} = {{\mathit{\boldsymbol{\dot l}}}_a} - \mathit{\boldsymbol{W}}{\left( {\mathit{\boldsymbol{\dot r}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right){{\mathit{\boldsymbol{\dot l}}}_b} $$ (19) $$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_2} = {{\mathit{\boldsymbol{\dot m}}}_a} - \left( {\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot s}}} \right) + \mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot s}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right)} \right){{\mathit{\boldsymbol{\dot l}}}_b} - }\\ {\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right){{\mathit{\boldsymbol{\dot m}}}_b}} \end{array} $$ (20) 当f=∑f12+∑f22最小时，即可得到相邻两个LiDAR点云测站坐标系之间的配准参数。
1.4 基于极值分析的LiDAR点云配准参数求解
1.4.1 旋转四元数${\mathit{\boldsymbol{\dot r}}}$的求解
为了实现对${\mathit{\boldsymbol{\dot r}}}$的求解，对∑f12的表达式分解如下：
$$ \begin{array}{*{20}{c}} {\sum {\mathit{\boldsymbol{f}}_1^2} = \sum {{{\mathit{\boldsymbol{\dot l}}}_a}^{\rm{T}}{{\mathit{\boldsymbol{\dot l}}}_a}} + \sum {{{\mathit{\boldsymbol{\dot l}}}_b}^{\rm{T}}{{\mathit{\boldsymbol{\dot l}}}_b}} - }\\ {2\sum {{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}{{\left( {{{\mathit{\boldsymbol{\dot l}}}_a}} \right)}^{\rm{T}}}\mathit{\boldsymbol{W}}\left( {{{\mathit{\boldsymbol{\dot l}}}_b}} \right)\mathit{\boldsymbol{\dot r}}} } \end{array} $$ (21) 令${\mathit{\boldsymbol{C}}_{l}} = \sum {\left({\mathit{\boldsymbol{\dot l}}_a^{\rm{T}}{{\mathit{\boldsymbol{\dot l}}}_a} + \mathit{\boldsymbol{\dot l}}_b^{\rm{T}}{{\mathit{\boldsymbol{\dot l}}}_b}} \right)} $，${\mathit{\boldsymbol{C}}_l} = {\rm{ }}-2\sum Q{({{\mathit{\boldsymbol{\dot l}}}_a})^{\rm{T}}} \cdot \mathit{\boldsymbol{W}}\left({{{\mathit{\boldsymbol{\dot l}}}_b}} \right)$，则：
$$ \mathit{\boldsymbol{f}}_1^2 = {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{l}}1}} + {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{l}}}\mathit{\boldsymbol{\dot r}} $$ (22) 最优的对偶四元数${\mathit{\boldsymbol{\dot r}}}$满足式(22)取得最小值的条件，同时，它也应该满足式(7)给出的条件，综合上述两个因素，构建目标函数F1为：
$$ {{\bar F}_1} = {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{l}}1}} + {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{l}}}\mathit{\boldsymbol{\dot r}} + {\mathit{\boldsymbol{\lambda }}_1}\left( {{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{\dot r}} - 1} \right) $$ (23) 式中，λ1是拉格朗日乘数。
对式(23)取偏导数有：
$$ \frac{{\partial {{\bar F}_1}}}{{\partial \mathit{\boldsymbol{\dot r}}}} = \left( {{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{l}}} + \mathit{\boldsymbol{C}}_\mathit{\boldsymbol{l}}^{\rm{T}}} \right)\mathit{\boldsymbol{\dot r}} + 2{\mathit{\boldsymbol{\lambda }}_1}\mathit{\boldsymbol{\dot r}} = 0 $$ (24) 根据式(24)可知，四元数${\mathit{\boldsymbol{\dot r}}}$是对应于矩阵(Cl + ClT)/2的一个特征向量，λ1是与特征向量相对应的特征值。构建矩阵A =-(Cl + ClT)/2，考虑到A是一个4×4的实对称阵，它的所有特征值和特征向量都是实数并且不同特征值对应的特征向量正交，与直线旋转变换相对应的四元数${\mathit{\boldsymbol{\dot r}}}$的期望值的确定还要进一步参考误差表达式(22)。
用${{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}$乘以式(24)有：
$$ {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{l}}}\mathit{\boldsymbol{\dot r}} = \frac{1}{2}{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{l}}} + \mathit{\boldsymbol{C}}_\mathit{\boldsymbol{l}}^{\rm{T}}} \right)\mathit{\boldsymbol{\dot r}} = - {\mathit{\boldsymbol{\lambda }}_1} $$ (25) 代入式(22)得：
$$ \mathit{\boldsymbol{f}}_1^2 = {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{l}}1}} - {\mathit{\boldsymbol{\lambda }}_1} $$ (26) 因此，当λ1选择最大特征值对应的特征向量时，变换前后同名线状方向向量之间的差异最小。
1.4.2 平移四元数${\mathit{\boldsymbol{\dot s}}}$的求解
为了实现对${\mathit{\boldsymbol{\dot s}}}$的求解，对∑f22的表达式分解如下：
$$ \begin{array}{*{20}{c}} {\sum {\mathit{\boldsymbol{f}}_2^2} = \sum {{{\mathit{\boldsymbol{\dot m'}}}_a}^{\rm{T}}{{\mathit{\boldsymbol{\dot m'}}}_a}} + \sum {\mathit{\boldsymbol{\dot l}}_b^{\rm{T}}{{\left[ {\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot s}}} \right)} \right]}^{\rm{T}}}\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot s}}} \right){{\mathit{\boldsymbol{\dot l}}}_b}} + }\\ {\sum {\mathit{\boldsymbol{\dot l}}_b^{\rm{T}}{{\left[ {\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot s}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right)} \right]}^{\rm{T}}}\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot s}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right){{\mathit{\boldsymbol{\dot l}}}_b}} - 2\sum {{{\mathit{\boldsymbol{\dot m'}}}_a}^{\rm{T}}\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot s}}} \right){{\mathit{\boldsymbol{\dot l}}}_b}} - }\\ {2\sum {{{\mathit{\boldsymbol{\dot m'}}}_a}^{\rm{T}}\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot s}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right){{\mathit{\boldsymbol{\dot l}}}_b}} + 2\sum {{{\left[ {\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot s}}} \right){{\mathit{\boldsymbol{\dot l}}}_b}} \right]}^{\rm{T}}}\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot s}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right){{\mathit{\boldsymbol{\dot l}}}_b}} } \end{array} $$ (27) 对式(27)的各组成部分进行分解，可得：
$$ \left\{ \begin{array}{l} \sum {\mathit{\boldsymbol{\dot l}}_b^{\rm{T}}{{\left[ {\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot s}}} \right)} \right]}^{\rm{T}}}\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot s}}} \right){{\mathit{\boldsymbol{\dot l}}}_b}} = \sum {{{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{I\dot s}}} \\ \sum {\mathit{\boldsymbol{\dot l}}_b^{\rm{T}}{{\left[ {\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot s}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right)} \right]}^{\rm{T}}}\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot s}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right){{\mathit{\boldsymbol{\dot l}}}_b}} = \sum {{{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{I\dot s}}} \\ - 2\sum {{{\mathit{\boldsymbol{\dot m'}}}_a}^{\rm{T}}\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot s}}} \right){{\mathit{\boldsymbol{\dot l}}}_b}} = - 2\sum {{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}{{\left( {{{\mathit{\boldsymbol{\dot m'}}}_a}} \right)}^{\rm{T}}}\mathit{\boldsymbol{W}}\left( {{{\mathit{\boldsymbol{\dot l}}}_b}} \right)\mathit{\boldsymbol{\dot s}}} \\ - 2\sum {{{\mathit{\boldsymbol{\dot m'}}}_a}^{\rm{T}}\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot s}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right){{\mathit{\boldsymbol{\dot l}}}_b}} = - 2\sum {{{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}{{\left( {{{\mathit{\boldsymbol{\dot m'}}}_a}} \right)}^{\rm{T}}}\mathit{\boldsymbol{W}}\left( {{{\mathit{\boldsymbol{\dot l}}}_b}} \right)\mathit{\boldsymbol{\dot r}}} \\ 2\sum {{{\left[ {\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot s}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right){{\mathit{\boldsymbol{\dot l}}}_b}} \right]}^{\rm{T}}}\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot s}}} \right){{\mathit{\boldsymbol{\dot l}}}_b}} = 2\sum {{{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{W'}}{{\left( {{{\mathit{\boldsymbol{\dot l}}}_b}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{W}}\left( {{{\mathit{\boldsymbol{\dot l}}}_b}} \right)\mathit{\boldsymbol{\dot s}}} \end{array} \right. $$ (28) 其中，$\mathit{\boldsymbol{W}}'\left({\mathit{\boldsymbol{\dot l}}} \right) = \left[{\begin{array}{*{20}{c}} 0 & {{l_1}} & {{l_2}} & {{l_3}}\\ {{l_1}} & 0 & {{l_3}} & {-{l_2}}\\ {{l_2}} & {-{l_3}} & 0 & {{l_1}}\\ {{l_3}} & {{l_2}} & {-{l_1}} & 0 \end{array}} \right]$。
令${\mathit{\boldsymbol{C}}_{m1}} = 2\sum \mathit{\boldsymbol{I}}$，${\mathit{\boldsymbol{C}}_{m2}} =-2\sum \mathit{\boldsymbol{Q}}{(\mathit{\boldsymbol{\dot m}}{\prime _a})^{\rm{T}}}\mathit{\boldsymbol{W}}({{\mathit{\boldsymbol{\dot l}}}_b})$，${\mathit{\boldsymbol{C}}_{m3}} = {\rm{ }}2\sum \mathit{\boldsymbol{W}}\prime {({{\mathit{\boldsymbol{\dot l}}}_b})^{\rm{T}}}\mathit{\boldsymbol{Q}}{(\mathit{\boldsymbol{\dot r}})^{\rm{T}}}\mathit{\boldsymbol{W}}{(\mathit{\boldsymbol{\dot r}})^{\rm{T}}}\mathit{\boldsymbol{W}}({{\mathit{\boldsymbol{\dot l}}}_b})$，${\mathit{\boldsymbol{C}}_m} = \sum (\mathit{\boldsymbol{\dot m}}{\prime _a}^{\rm{T}}\mathit{\boldsymbol{\dot m}}{\prime _a})$，则式(27)可进一步表达为：
$$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{f}}_2^2 = {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_{m1}}\mathit{\boldsymbol{\dot s}} + {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_{m2}}\mathit{\boldsymbol{\dot s}} + {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_{m2}}\mathit{\boldsymbol{\dot r}} + }\\ {{{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_{m3}}\mathit{\boldsymbol{\dot s}} + {\mathit{\boldsymbol{C}}_m}} \end{array} $$ (29) 与旋转四元数${\mathit{\boldsymbol{\dot r}}}$的求解方法类似，通过附加约束条件到误差方程中，构建目标函数F2：
$$ \begin{array}{*{20}{c}} {{{\bar F}_2} = {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_{m1}}\mathit{\boldsymbol{\dot s}} + {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_{m2}}\mathit{\boldsymbol{\dot s}} + {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_{m2}}\mathit{\boldsymbol{\dot r}} + {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_{m3}}\mathit{\boldsymbol{\dot s}} + }\\ {{\mathit{\boldsymbol{C}}_m} + {\mathit{\boldsymbol{\lambda }}_2}\left( {{{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{\dot r}}} \right)} \end{array} $$ (30) 式中，λ2是拉格朗日乘数。
对式(30)取偏导数，可得${\mathit{\boldsymbol{\dot s}}}$的表达式为：
$$ \mathit{\boldsymbol{\dot s}} = - {\mathit{\boldsymbol{C}}_s}\left( {{\mathit{\boldsymbol{C}}_{m2}} + \mathit{\boldsymbol{C}}_{m2}^{\rm{T}}} \right)\mathit{\boldsymbol{\dot r}} - {\mathit{\boldsymbol{\lambda }}_2}{\mathit{\boldsymbol{C}}_s}\mathit{\boldsymbol{\dot r}} $$ (31) 其中，${\mathit{\boldsymbol{C}}_s} = {\left[{\left({{\mathit{\boldsymbol{C}}_{m1}} + \mathit{\boldsymbol{C}}_{m1}^{\rm{T}}} \right) + \left({{\mathit{\boldsymbol{C}}_{m3}} + \mathit{\boldsymbol{C}}_{m3}^{\rm{T}}} \right)} \right]^{ -1}}$。
考虑式(7)中所表达的对偶四元数的附加约束条件，用${{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}$乘以等式(31)，可得系数λ2的表达式：
$$ {\mathit{\boldsymbol{\lambda }}_2} = - \frac{{{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_s}\left( {{\mathit{\boldsymbol{C}}_{m2}} + \mathit{\boldsymbol{C}}_{m2}^{\rm{T}}} \right)\mathit{\boldsymbol{\dot r}}}}{{{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_s}\mathit{\boldsymbol{\dot r}}}} $$ (32) 求得了${\mathit{\boldsymbol{\dot s}}}$与${\mathit{\boldsymbol{\dot r}}}$，即可求得${\mathit{\boldsymbol{\dot t}}}$：
$$ \mathit{\boldsymbol{\dot t}} = 2\mathit{\boldsymbol{\dot s}}{{\mathit{\boldsymbol{\dot r}}}^ * } $$ (33) 1.4.3 算法实现流程
已知(la, ma)、(lb, mb)分别为基准站、待配准站同名线状特征的方向向量与矩，$\left({{{\mathit{\boldsymbol{\dot l}}}_a}, {{\mathit{\boldsymbol{\dot m}}}_a}} \right)$、$\left({{{\mathit{\boldsymbol{\dot l}}}_b}, {{\mathit{\boldsymbol{\dot m}}}_b}} \right)$为与线特征相对应的四元数，利用本文算法来实现相邻测站LiDAR点云的配准，算法实现的流程如图 3所示。
1) 根据式(24)构建矩阵A =-(Cl + ClT)/2，求解矩阵A的最大特征值对应的特征向量${\mathit{\boldsymbol{\dot r}}}$，并通过表达式$\mathit{\boldsymbol{R = W}}{\left({\mathit{\boldsymbol{\dot r}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Q}}\left({\mathit{\boldsymbol{\dot r}}} \right)$计算旋转矩阵。
2) 分别构建Cm1、Cm2与Cm3等矩阵，通过式(32)计算λ2的值。
3) 通过式(31)计算得到${\mathit{\boldsymbol{\dot s}}}$的值，通过式(33)计算得到${\mathit{\boldsymbol{\dot t}}}$的值。
经过上述计算，即可得到相邻两个测站LiDAR点云配准的计算结果。
需要指出的是，因算法实现中需要求解6个未知参数，而三维空间中直线的自由度为4，因此，算法的正确运行需要至少两对相交或异面的线状特征来提供约束。
2 LiDAR点云配准实例与分析
本文提出的线状特征约束下利用Plücker直线坐标描述的LiDAR点云配准算法已经通过C++编程实现，为了验证算法的有效性与实用性，设计了两个实验：利用奥地利Riegl公司生产的LMS-Z420i系列地面LiDAR设备分别在室外与室内采集了若干组点云数据，通过人机交互的方式来实现位于同一平面的LiDAR点云的选择，通过平面拟合与相交算法来实现最终线状特征的提取。
2.1 实验1
图 4所示为LMS-Z420i系列地面LiDAR设备采集得到的某建筑物立面点云，分别从两个相邻测站提取了表 1所示的7对同名线状特征，用以测试算法的可行性。同时，为了对算法运行结果的正确性进行验证，将表 1所示同名特征代入文献[12]中所阐述的算法，并对二者的运行结果进行对比与分析。
![]()
图 4 同一建筑物采集得到的立面LiDAR点云Figure 4. Two Neighboring LiDAR Point Clouds Acquired from the Same Building表 1 从两相邻测站提取的7对同名线状特征Table 1. Seven Linear Features Extracted from Neighbor Stations线段编号 基准测站 待配准测站 起点坐标 终点坐标 起点坐标 终点坐标 x/m y/m z/m x/m y/m z/m x/m y/m z/m x/m y/m z/m 1 -47.545 -29.207 23.066 -48.845 -27.906 23.054 -54.468 -39.362 13.116 -55.010 -37.361 13.019 2 -72.672 -8.306 25.901 -68.763 -4.408 25.915 -66.382 -8.682 13.949 -60.446 -7.021 15.317 3 -49.959 14.310 25.545 -49.906 14.262 18.937 -36.241 -0.278 20.528 -34.627 -0.217 13.396 4 -49.903 14.328 22.703 -74.119 38.575 22.390 -42.692 26.285 16.339 -44.524 33.100 15.991 5 -58.342 22.763 25.800 -62.807 27.248 25.733 -39.251 10.796 20.250 -41.006 17.368 19.910 6 -63.026 27.457 18.813 -63.000 27.423 14.990 -39.544 17.731 13.030 -38.725 17.757 9.383 7 -59.337 23.730 22.619 -62.802 27.215 22.561 -39.004 12.439 17.069 -40.287 17.253 16.816 表 2 线状特征约束下基于四元数的LiDAR点云配准结果及其与现有算法运行结果的对比(实验1)Table 2. Results Comparison of the Proposed Algorithm and Reference [12](Experiment 1)测试方案 旋转矩阵R 平移T/m 配准后同名特征的单位方向向量偏差 线状特征的矩偏差及其中误差 Δ lx Δ ly Δ lz Δ mx/m Δ my/m Δ mz/m mΔ m 本文算法 0.000 5 0.000 5 0.000 1 -0.007 4 0.020 7 -0.007 7 -0.000 2 0.000 2 0.000 3 0.001 8 0.005 9 -0.008 1 0.850 3 -0.494 6 0.180 0 -22.978 3 0.000 1 -0.000 2 0.000 0 0.014 7 0.002 2 0.010 0 0.479 4 0.868 9 0.123 1 29.405 9 -0.000 2 -0.000 2 0.000 3 0.017 8 0.018 1 0.020 7 0.023 6 -0.217 3 -0.018 4 0.975 9 -2.287 2 -0.000 2 -0.000 2 -0.000 1 0.003 6 -0.009 0 0.013 4 -0.000 4 0.000 2 -0.000 0 0.002 4 -0.007 8 0.000 1 0.000 1 0.000 1 -0.000 5 -0.013 4 -0.026 2 -0.010 2 文献[12]算法 0.000 5 0.000 5 0.000 1 -0.012 8 0.015 5 0.000 4 -0.000 2 0.000 2 0.000 3 -0.003 2 0.010 9 -0.011 0 0.850 3 -0.494 6 0.180 0 -22.977 4 0.000 1 -0.000 2 0.000 0 0.008 9 0.004 0 0.010 0 0.479 4 0.868 9 0.123 1 29.401 5 -0.000 2 -0.000 2 0.000 3 0.012 4 0.012 8 0.026 0 0.025 1 -0.217 3 -0.018 4 0.975 9 -2.297 1 -0.000 2 -0.000 2 -0.000 1 -0.001 5 -0.014 1 0.018 8 -0.000 4 0.000 2 -0.000 0 -0.002 1 -0.004 7 0.000 0 0.000 1 0.000 1 -0.000 5 -0.018 8 -0.031 5 -0.004 8 基于本文的配准参数，对图 4所示的两个相邻测站LiDAR点云进行配准，配准前后的目视效果如图 5所示。
根据图 5所示效果来看，本文算法的运行结果与设计初衷一致，可以用于线状特征约束下相邻测站LiDAR点云的配准。根据表 2所示的两个算法的运行结果，可以得出如下结论：(1)在旋转变换矩阵的计算上，本文算法与文献[12]所述算法结果完全相同，因此，配准后同名特征之间的方向偏差完全一致；(2)利用本文算法与文献[12]所述算法配准所得的相邻两个测站之间的平移参数略有偏差，间接导致了配准后同名线状特征的矩之间存在偏差，利用白赛尔公式计算两种算法结果的矩偏差中误差mΔm分别为0.023 6与0.025 1，本文算法略优于文献[12]所述算法。
2.2 实验2
此实验所用数据同样是由LMS-Z420i系列地面LiDAR设备采集得到，不同的是本次实验数据的采集工作选择在室内进行，在两个相邻的测站中提取了8对同名线状特征(如表 3所示)之后，利用本文算法对相邻两个测站进行了配准，结果如表 4所示。
表 3 从两相邻测站提取的8对同名线状特征Table 3. Eight Linear Features Extracted from Neighbor Stations线段编号 基准测站 待配准测站 起点坐标 终点坐标 起点坐标 终点坐标 x/m y/m z/m x/m y/m z/m x/m y/m z/m x/m y/m z/m 1 -9.154 9.583 7.885 -4.932 9.416 7.887 -11.352 5.786 8.199 5.493 6.842 4.968 2 -14.826 -1.021 7.880 -14.443 9.207 7.880 -11.521 -5.174 9.616 -12.423 5.135 8.479 3 4.653 8.474 7.894 4.244 -1.769 7.891 6.299 6.354 4.880 7.610 -8.815 6.563 4 -14.832 -1.159 7.880 4.253 -1.907 7.891 -7.944 -4.932 8.930 -2.611 -4.580 7.902 5 -5.757 -1.516 7.900 -5.753 -1.544 3.225 -2.618 -4.578 7.924 -3.810 -5.405 1.415 6 -5.975 -7.086 7.902 -5.969 -7.077 2.994 -2.160 -10.098 8.472 -3.012 -10.674 3.830 7 4.668 9.016 2.816 4.675 9.005 7.847 5.333 6.270 -0.147 6.257 6.890 4.842 8 -14.830 -1.159 7.841 -14.824 -1.192 2.765 -11.530 -5.155 9.574 -12.529 -5.872 4.096 表 4 线状特征约束下基于四元数的LiDAR点云配准结果及其与现有算法运行结果的对比(实验2)Table 4. Results Comparison of the Proposed Algorithm and Reference [12](Experiment 2)测试方案 旋转矩阵R 平移T/m 配准后同名特征的单位方向向量偏差 线状特征的矩偏差及其中误差 Δ lx Δ ly Δ lz Δ mx/m Δ my/m Δ mz/m mΔ m 本文算法 0.000 1 0.001 8 0.000 0 -0.013 3 0.010 0 -0.014 2 -0.000 4 0.000 0 0.001 1 0.005 5 0.013 8 -0.000 1 0.975 9 0.102 3 -0.192 8 -1.206 5 -0.001 0 0.000 0 -0.001 9 -0.003 3 0.000 6 0.005 2 -0.123 4 0.987 2 -0.100 9 3.470 8 -0.000 0 -0.001 2 0.000 7 0.008 0 -0.001 6 -0.004 0 0.018 2 0.180 0 0.122 3 0.976 0 1.207 5 -0.000 2 -0.004 1 0.000 0 0.023 2 -0.001 2 0.023 3 0.000 3 0.000 8 0.000 0 -0.006 9 0.007 6 -0.002 8 0.000 7 -0.001 1 -0.000 0 0.001 8 0.001 6 -0.011 9 -0.000 2 -0.000 8 0.000 0 -0.013 3 0.010 0 -0.014 2 文献[12]算法 0.000 1 0.001 8 0.000 0 -0.013 6 0.003 2 -0.012 3 -0.000 4 0.000 0 0.001 1 0.012 2 0.013 5 -0.003 0 0.975 9 0.102 3 -0.192 8 -1.205 6 -0.001 0 0.000 0 -0.001 9 -0.010 0 0.000 8 0.005 1 -0.123 4 0.987 2 -0.100 9 3.473 5 0.000 0 -0.001 2 0.000 7 0.007 8 -0.008 4 -0.000 6 0.019 3 0.180 0 0.122 3 0.976 0 1.215 2 -0.000 2 -0.004 1 0.000 0 0.026 6 -0.002 8 0.023 3 0.000 3 0.000 8 0.000 0 -0.002 6 0.006 0 -0.002 8 0.000 7 -0.001 1 0.000 0 -0.000 1 0.001 6 -0.011 9 对比表 4所得的两个算法的运行结果，所得结论与§2.1所得结论完全一致。
3 结语
作为现实中最为常见的几何特征之一，线状特征的引入将为LiDAR点云的配准提供更为丰富的约束条件以及更为可靠的质量保证。Plücker直线坐标的引入克服了经典的向量代数在线状特征表达与描述中的多样性问题，为LiDAR点云配准算法的设计提供了便利。最为重要的是，本文算法的运行无需事先确定配准参数的初值，避免了多元函数的线性化过程，解除了参数结果对于迭代初值的依赖，克服了迭代法在求解大转角相似变换参数时的算法不稳定问题。
需要指出的是，作为空间相似变换的一个特例，刚体变换的应用领域仍然存在较大的局限性，因此，进一步工作将着眼于如何在本文的算法模型中引入缩放系数，构建线状特征约束下三维空间相似变换的无初值求解模型，为其在多源数据融合中的进一步应用提供理论基础。参考文献
-
![]()
图 1 对偶四元数表示的旋转和平移
Figure 1. Dual Quaternion Based Representation of Rotation and Translation
![]()
图 2 三维空间中基于Plücker坐标的直线表达
Figure 2. Plücker-based Representation of a Line in 3D Space
![]()
图 4 同一建筑物采集得到的立面LiDAR点云
Figure 4. Two Neighboring LiDAR Point Clouds Acquired from the Same Building
表 1 从两相邻测站提取的7对同名线状特征
Table 1 Seven Linear Features Extracted from Neighbor Stations
线段编号 基准测站 待配准测站 起点坐标 终点坐标 起点坐标 终点坐标 x/m y/m z/m x/m y/m z/m x/m y/m z/m x/m y/m z/m 1 -47.545 -29.207 23.066 -48.845 -27.906 23.054 -54.468 -39.362 13.116 -55.010 -37.361 13.019 2 -72.672 -8.306 25.901 -68.763 -4.408 25.915 -66.382 -8.682 13.949 -60.446 -7.021 15.317 3 -49.959 14.310 25.545 -49.906 14.262 18.937 -36.241 -0.278 20.528 -34.627 -0.217 13.396 4 -49.903 14.328 22.703 -74.119 38.575 22.390 -42.692 26.285 16.339 -44.524 33.100 15.991 5 -58.342 22.763 25.800 -62.807 27.248 25.733 -39.251 10.796 20.250 -41.006 17.368 19.910 6 -63.026 27.457 18.813 -63.000 27.423 14.990 -39.544 17.731 13.030 -38.725 17.757 9.383 7 -59.337 23.730 22.619 -62.802 27.215 22.561 -39.004 12.439 17.069 -40.287 17.253 16.816 
下载: 导出CSV
表 2 线状特征约束下基于四元数的LiDAR点云配准结果及其与现有算法运行结果的对比(实验1)
Table 2 Results Comparison of the Proposed Algorithm and Reference [12](Experiment 1)
测试方案 旋转矩阵R 平移T/m 配准后同名特征的单位方向向量偏差 线状特征的矩偏差及其中误差 Δ lx Δ ly Δ lz Δ mx/m Δ my/m Δ mz/m mΔ m 本文算法 0.000 5 0.000 5 0.000 1 -0.007 4 0.020 7 -0.007 7 -0.000 2 0.000 2 0.000 3 0.001 8 0.005 9 -0.008 1 0.850 3 -0.494 6 0.180 0 -22.978 3 0.000 1 -0.000 2 0.000 0 0.014 7 0.002 2 0.010 0 0.479 4 0.868 9 0.123 1 29.405 9 -0.000 2 -0.000 2 0.000 3 0.017 8 0.018 1 0.020 7 0.023 6 -0.217 3 -0.018 4 0.975 9 -2.287 2 -0.000 2 -0.000 2 -0.000 1 0.003 6 -0.009 0 0.013 4 -0.000 4 0.000 2 -0.000 0 0.002 4 -0.007 8 0.000 1 0.000 1 0.000 1 -0.000 5 -0.013 4 -0.026 2 -0.010 2 文献[12]算法 0.000 5 0.000 5 0.000 1 -0.012 8 0.015 5 0.000 4 -0.000 2 0.000 2 0.000 3 -0.003 2 0.010 9 -0.011 0 0.850 3 -0.494 6 0.180 0 -22.977 4 0.000 1 -0.000 2 0.000 0 0.008 9 0.004 0 0.010 0 0.479 4 0.868 9 0.123 1 29.401 5 -0.000 2 -0.000 2 0.000 3 0.012 4 0.012 8 0.026 0 0.025 1 -0.217 3 -0.018 4 0.975 9 -2.297 1 -0.000 2 -0.000 2 -0.000 1 -0.001 5 -0.014 1 0.018 8 -0.000 4 0.000 2 -0.000 0 -0.002 1 -0.004 7 0.000 0 0.000 1 0.000 1 -0.000 5 -0.018 8 -0.031 5 -0.004 8
下载: 导出CSV
表 3 从两相邻测站提取的8对同名线状特征
Table 3 Eight Linear Features Extracted from Neighbor Stations
线段编号 基准测站 待配准测站 起点坐标 终点坐标 起点坐标 终点坐标 x/m y/m z/m x/m y/m z/m x/m y/m z/m x/m y/m z/m 1 -9.154 9.583 7.885 -4.932 9.416 7.887 -11.352 5.786 8.199 5.493 6.842 4.968 2 -14.826 -1.021 7.880 -14.443 9.207 7.880 -11.521 -5.174 9.616 -12.423 5.135 8.479 3 4.653 8.474 7.894 4.244 -1.769 7.891 6.299 6.354 4.880 7.610 -8.815 6.563 4 -14.832 -1.159 7.880 4.253 -1.907 7.891 -7.944 -4.932 8.930 -2.611 -4.580 7.902 5 -5.757 -1.516 7.900 -5.753 -1.544 3.225 -2.618 -4.578 7.924 -3.810 -5.405 1.415 6 -5.975 -7.086 7.902 -5.969 -7.077 2.994 -2.160 -10.098 8.472 -3.012 -10.674 3.830 7 4.668 9.016 2.816 4.675 9.005 7.847 5.333 6.270 -0.147 6.257 6.890 4.842 8 -14.830 -1.159 7.841 -14.824 -1.192 2.765 -11.530 -5.155 9.574 -12.529 -5.872 4.096
下载: 导出CSV
表 4 线状特征约束下基于四元数的LiDAR点云配准结果及其与现有算法运行结果的对比(实验2)
Table 4 Results Comparison of the Proposed Algorithm and Reference [12](Experiment 2)
测试方案 旋转矩阵R 平移T/m 配准后同名特征的单位方向向量偏差 线状特征的矩偏差及其中误差 Δ lx Δ ly Δ lz Δ mx/m Δ my/m Δ mz/m mΔ m 本文算法 0.000 1 0.001 8 0.000 0 -0.013 3 0.010 0 -0.014 2 -0.000 4 0.000 0 0.001 1 0.005 5 0.013 8 -0.000 1 0.975 9 0.102 3 -0.192 8 -1.206 5 -0.001 0 0.000 0 -0.001 9 -0.003 3 0.000 6 0.005 2 -0.123 4 0.987 2 -0.100 9 3.470 8 -0.000 0 -0.001 2 0.000 7 0.008 0 -0.001 6 -0.004 0 0.018 2 0.180 0 0.122 3 0.976 0 1.207 5 -0.000 2 -0.004 1 0.000 0 0.023 2 -0.001 2 0.023 3 0.000 3 0.000 8 0.000 0 -0.006 9 0.007 6 -0.002 8 0.000 7 -0.001 1 -0.000 0 0.001 8 0.001 6 -0.011 9 -0.000 2 -0.000 8 0.000 0 -0.013 3 0.010 0 -0.014 2 文献[12]算法 0.000 1 0.001 8 0.000 0 -0.013 6 0.003 2 -0.012 3 -0.000 4 0.000 0 0.001 1 0.012 2 0.013 5 -0.003 0 0.975 9 0.102 3 -0.192 8 -1.205 6 -0.001 0 0.000 0 -0.001 9 -0.010 0 0.000 8 0.005 1 -0.123 4 0.987 2 -0.100 9 3.473 5 0.000 0 -0.001 2 0.000 7 0.007 8 -0.008 4 -0.000 6 0.019 3 0.180 0 0.122 3 0.976 0 1.215 2 -0.000 2 -0.004 1 0.000 0 0.026 6 -0.002 8 0.023 3 0.000 3 0.000 8 0.000 0 -0.002 6 0.006 0 -0.002 8 0.000 7 -0.001 1 0.000 0 -0.000 1 0.001 6 -0.011 9
下载: 导出CSV
-
[1] Horn B K. Closed Form Solution of Absolute Orientation Using Orthonormal Matrices[J]. Journal of Optical Society of America, Series A, 1988, 5(7):1127-1135 doi: 10.1364/JOSAA.5.001127
[2] Arun K S, Huang T S. Least-Squares Fitting of Two 3D Point Sets[J]. IEEE Trans Pattern Analysis and Machine Intelligence, 1987, 9(5):698-700 https://www.wenkuxiazai.com/doc/c3f145d9e87101f69f319596-3.html
[3] Horn B K. Closed-Form Solution of Absolute Orientation Using Unit Quaternions[J]. Journal of Optical Society of America, Series A, 1987, 4(4):629-642 doi: 10.1364/JOSAA.4.000629
[4] Shen Y Z, Chen Y, Zheng D H. A Quaternion-Based Geodetic Datum Transformation Algorithm[J]. Journal of Geodesy, 2006, 80:233-239 doi: 10.1007/s00190-006-0054-8
[5] Walker M W, Shao L, Volz R A. Estimating 3D Location Parameters Using Dual Number Quater-nions[J]. CVGIP:Image Understanding, 1991, 54(3):358-367 doi: 10.1016/1049-9660(91)90036-O
[6] Prošková J. Application of Dual Quaternions Algorithm for Geodetic Datum Transformation[J]. Journal of Applied Mathematics, 2011, 4(2):225-236 https://www.sciencedirect.com/science/article/pii/S0924271614001087
[7] Prošková J. Discovery of Dual Quaternions for Geo-desy[J]. Journal for Geometry and Graphics, 2012, 16(2):195-209 http://ieeexplore.ieee.org/document/6882186/
[8] 龚辉, 江刚武, 姜挺, 等.基于对偶四元数的绝对定向直接解法[J].测绘科学技术学报, 2009, 26(6):434-438 doi: 10.3969/j.issn.1673-6338.2009.06.012 Gong Hui, Jiang Gangwu, Jiang Ting, et al. Close-Form Solution of Absolute Orientation Based on Dual Quaternion[J]. Journal of Geomatics Science and Technology, 2009, 26(6):434-438 doi: 10.3969/j.issn.1673-6338.2009.06.012
[9] Wang Yongbo, Wang Yunjia, Wu Kan, et al. A Dual Quaternion-Based, Closed-Form Pairwise Re-gistration Algorithm for Point Clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 94:63-69 doi: 10.1016/j.isprsjprs.2014.04.013
[10] Habib A, Mwafag G, Michel M, et al. Photogrammetric and LiDAR Data Registration Using Linear Features[J]. Photogrammetric Engineering & Remote Sensing, 2005, 71(6):699-707 http://d.old.wanfangdata.com.cn/Conference/WFHYXW328667
[11] Daniilidis K. Hand-Eye Calibration Using Dual Quaternions[J]. The International Journal of Robotics Research, 1999, 18(3):286-298 doi: 10.1177/02783649922066213
[12] 王永波, 杨化超, 刘燕华, 等.线状特征约束下基于四元数描述的LiDAR点云配准方法[J].武汉大学学报·信息科学版, 2013, 38(9):1057-1062 http://ch.whu.edu.cn/CN/abstract/abstract2751.shtml Wang Yongbo, Yang Huachao, Liu Yanhua, et al. Linear-Feature-Constrained Registration of LiDAR Point Cloud via Quaternion[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9):1057-1062 http://ch.whu.edu.cn/CN/abstract/abstract2751.shtml
[13] Renaudin E, Habib A, Kersting A. Featured-Based Registration of Terrestrial Laser Scans with Minimum Overlap Using Photogrammetric Data[J]. ETRI Journal, 2011, 33(4):517-527 doi: 10.4218/etrij.11.1610.0006
[14] He F, Habib A. A Closed-Form Solution for Coarse Registration of Point Clouds Using Linear Features[J]. Journal of Survey and Engineering, 2016, 142(3):04016006, DOI:10.1061/(ASCE) SU.1943-5428. 0000174
[15] 盛庆红, 陈姝文, 柳建锋, 等.基于Plücker直线的LiDAR点云配准法[J].测绘学报, 2016, 45(1):58-64 http://d.old.wanfangdata.com.cn/Periodical/chxb201601009 Sheng Qinghong, Chen Shuwen, Liu Jianfeng, et al. LiDAR Point Cloud Registration Based on Plücker Line[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1):58-64 http://d.old.wanfangdata.com.cn/Periodical/chxb201601009
[16] Khoshelham K. Closed-Form Solutions for Estimating a Rigid Motion from Plane Correspondences Extracted from Point Clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 114:78-91 doi: 10.1016/j.isprsjprs.2016.01.010
[17] 郑德华, 岳东杰, 岳建平.基于几何特征约束的建筑物点云配准算法[J].测绘学报, 2008, 37(4):464-468 doi: 10.3321/j.issn:1001-1595.2008.04.011 Zheng Dehua, Yue Dongjie, Yue Jianping. Geome-tric Feature Constraint Based Algorithm for Buil-ding Scanning Point Cloud Registration[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4):464-468 doi: 10.3321/j.issn:1001-1595.2008.04.011
[18] Pottmann H, Hofer M, Odehnal B, et al. Line Geometry for 3D Shape Understanding and Reconstruction[C]. European Conference on Computer Vision, Prague, Czech Republic, 2004
-
期刊类型引用(13)
1. 方浩，李红军. 点云数据直线检测及其在人工林树木计数中的应用. 武汉大学学报(信息科学版). 2024(02): 208-215 . 
百度学术
2. 陈淋，张同刚，王鑫，李文君，陈婷婷，炊宇恒，熊鑫. 基于线对间法向距离特征的机载和车载点云配准算法. 测绘与空间地理信息. 2024(12): 167-170 . 百度学术
3. 柴双武. 基于对偶四元数描述的扩展平面基元点云拼接方法. 北京测绘. 2023(06): 823-828 . 百度学术
4. 李绕波，袁希平，甘淑，毕瑞，高莎，胡琳. 点面特征约束下利用对偶四元素描述的点云配准模型求解方法. 武汉大学学报(信息科学版). 2023(09): 1546-1554 . 百度学术
5. 鲍国，张书毕，陈强，郑有雷，陈春. 基于地面LiDAR的建筑物精细化三维重建及精度分析. 金属矿山. 2023(09): 140-144 . 百度学术
6. 李绕波，袁希平，甘淑，毕瑞，高莎，郭燕. 一种基于对偶四元素描述的线面特征约束的点云配准方法. 光学学报. 2022(02): 167-175 . 百度学术
7. 宁悦. 三维点云配准方法研究. 测绘与空间地理信息. 2022(07): 188-191 . 百度学术
8. 王家晖，姚吉利，赵雪莹，胡信志，赵猛. 基于点线面混合控制基元的点云地理化. 激光与光电子学进展. 2021(08): 423-430 . 百度学术
9. 杜伟，刘洋，杨国柱，王和平，李致东，李俊磊，习晓环. 输电通道机载激光点云多级配准研究. 遥感技术与应用. 2021(06): 1294-1298 . 百度学术
10. 柴双武，杨晓琴. 基于点面关系构建的线基元点云配准算法. 大地测量与地球动力学. 2020(04): 405-410 . 百度学术
11. 王建，姚吉利，赵雪莹，赵猛，杨承昆，李彩林. 点线混合控制基元的点云地理化参数联合解算. 武汉大学学报(信息科学版). 2020(05): 760-767 . 百度学术
12. 柴双武，杨晓琴. 基于对偶四元数构建的直线基元点云拼接方法. 光学学报. 2019(12): 416-424 . 百度学术
13. 朱庆，李世明，胡翰，钟若飞，吴波，谢林甫. 面向三维城市建模的多点云数据融合方法综述. 武汉大学学报(信息科学版). 2018(12): 1962-1971 . 百度学术
其他类型引用(11)
计量
- 文章访问数: 1453
- HTML全文浏览量: 127
- PDF下载量: 294
- 被引次数: 24
