The Effect of the Random Coefficient Matrix on Adjustment of the Inversion of Crustal Strain Parameters Model
-
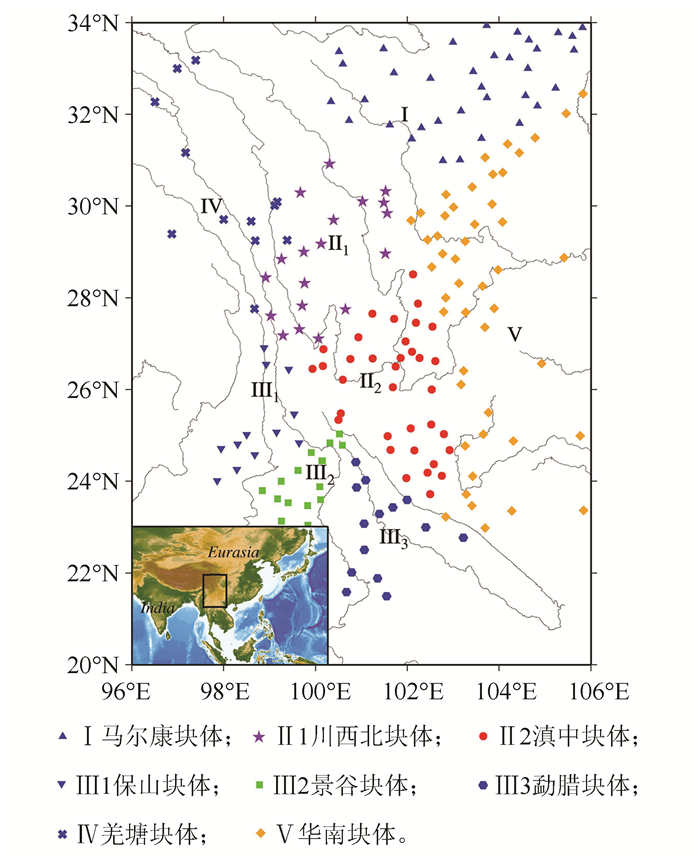
摘要: 针对地壳应变参数反演模型中系数矩阵含随机和非随机元素及观测数据存在相关性等情况，以部分变量误差（partial-errors-in-variables，PEIV）模型为基础，采用了地壳应变参数反演的加权总体最小二乘算法，该算法不受系数矩阵和权矩阵结构的限制，能够快速、有效解决系数矩阵含有随机误差的模型问题。结合推导得到的最小二乘改正项公式，对地壳反演模型中坐标点误差对反演参数求解的影响进行了分析。通过对模拟数据和川滇地区的实际数据进行处理，得出系数矩阵误差对地壳应变参数反演的影响主要受GPS站点坐标值量级以及应变参数量级的牵制。Abstract: Theweighted total least squares method based on partial errors-in-variables (PEIV for short) model is used to solve the inversion parameters of crustal strain model. It not only considers the error of observation (displacement or velocity field), but also the error effects from the coefficient matrix, generally composed of monitoring points coordinates. When taking the special structure of the coefficient matrix in the geodetic inversion model into account, we insure that the repeated coordinates have the same residual and that the constants are not allocated any correction. The method usedin this paper can meet these requirements as it separates the random elements from the constant elements taking advantage of the partial errors-in-variables model. All calculation formulae for crust strain (rate) parameters inversion based on partial errors-in-variables using monitoring point displacement or velocity fields are deduced. In addition, the derivate correction of weighted least squares (WLS) is used to analyze the effect of the random coefficient. The discrepancy between the weighted least squares solution and WTLS solution was also investigated. Because of the complexity of the WTLS solution, we propose a formulation to relate the WLS\and WTLS solutions based on Xu (J Geod 86:661-675, 2012). A simulation using data from the Sichuan-Yunnan region permits a comparison and analysis of the effect of the random design matrix. The experimental results reveal that the effect of the random coefficient matrix on adjustment of the inversion of crustal strain (rate) parameters model is mainly depend on the order of value of the GPS coordinates and the crustal strain parameters themselves.
-
-
![]()
图 1 方案1中地壳应变参数反演的模拟站点
Figure 1. Simulated Network Stations of the Inversion of Crustal Strain in Case 1
![]()
图 2 各方案观测向量和系数矩阵随机元素残差值(PEIV-WTLS)
Figure 2. Residuals of Observation Vector and Coefficient Matrix in Each Case(PEIV-WTLS)
![]()
![]()
图 4 川滇地区地壳应变参数反演过程中观测向量和系数矩阵随机元素残差值
Figure 4. Residuals of Observation Vector and Coefficient Matrix in the Region of Sichuan and Yunnan
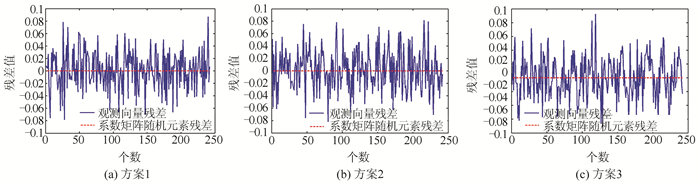
表 1 各方案的情景设置
Table 1 The Scene of the Three Schemes
方案1 方案2 方案3 区域 100 m×100 m 200 m×200 m 1 000 m×1 000 m 采样间隔 沿x、y轴每隔10 m 沿x、y轴每隔20 m 沿x、y轴每隔100 m 坐标点总数(采样) 121个 121个 121个 模拟应变参数真值 εx=200×10-8
εy=-80×10-8
εxy=1 000×10-8
ω=1 100×10-8εx=200×10-9
εy=-80×10-9
εxy=1 000×10-9
ω=1 100×10-9εx=200×10-10
εy=-80×10-10
εxy=1 000×10-10
ω=1 100×10-10
下载: 导出CSV
表 2 各方案参数计算结果
Table 2 Results of Parameters in Each Case
εx εy εxy w 方案1 真值 200×10-8 -80×10-8 1 000×10-8 1 100×10-8 WLS 189×10-8 -86×10-8 1 006×10-8 1 097×10-8 PEIV-WTLS 189×10-8 -86×10-8 1 006×10-8 1 097×10-8 b -1.5×10-18 2.6×10-17 -1.5×10-17 -1.7×10-17 方案2 真值 200×10-9 -80×10-9 1000×10-9 1100×10-9 WLS 195×10-9 -81×10-9 1005×10-9 1100×10-9 PEIV-WTLS 195×10-9 -81×10-9 1005×10-9 1100×10-9 b -3.2×10-21 8.9×10-21 -4.8×10-21 -7.1×10-21 方案3 真值 200×10-10 -80×10-10 1 000×10-10 1 100×10-10 WLS 202×10-10 -83×10-10 999×10-10 1 103×10-10 PEIV-WTLS 202×10-10 -83×10-10 999×10-10 1 103×10-10 b -2.9×10-23 9.8×10-23 -1.0×10-22 -1.2×10-22
下载: 导出CSV
表 3 各块体应变率参数计算改正项b结果
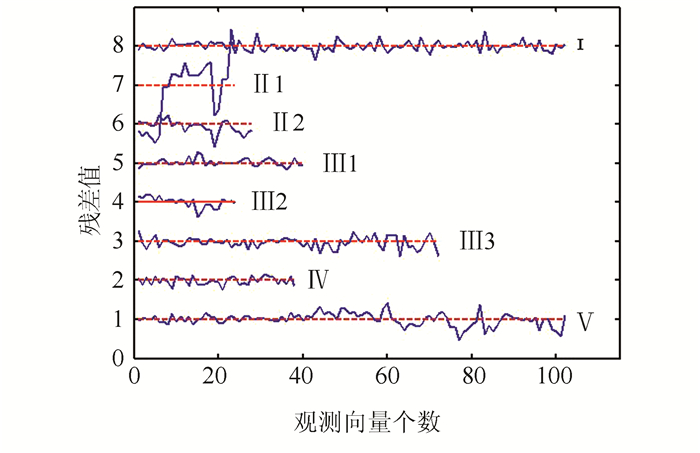
Table 3 The Calculation Results of Each Block Strain Rate Parameter
改正项 u/a v/a εx/a εy/a εxy/a ω/a bⅠ -5.6×10-16 -2.2×10-15 -4.4×10-22 8.7×10-24 1.9×10-23 6.9×10-23 bⅡ1 2.2×10-15 -1.2×10-15 3.1×10-23 -1.6×10-23 -3.4×10-23 -5.0×10-23 bⅡ2 2.2×10-15 7.5×10-18 1.2×10-24 -4.5×10-25 -2.7×10-24 -4.3×10-24 bⅢ1 -2.7×10-15 9.4×10-15 1.6×10-20 -1.1×10-21 -2.7×10-21 -2.5×10-21 bⅢ2 8.6×10-16 2.1×10-15 1.7×10-23 -2.4×10-23 -2.8×10-24 -1.2×10-24 bⅢ3 -3.4×10-13 5.4×10-13 5.3×10-22 2.2×10-22 3.0×10-22 1.8×10-22 bⅣ 1.8×10-13 1.8×10-13 -1.3×10-20 -4.8×10-22 -6.9×10-21 -6.4×10-21 bⅤ -5.6×10-16 -3.7×10-16 -1.9×10-24 7.1×10-25 5.4×10-26 1.2×10-24
下载: 导出CSV
-
[1] 许才军.大地测量联合反演理论和方法研究进展[J].武汉大学学报·信息科学版, 2001, 26(6):555-561 http://ch.whu.edu.cn/CN/abstract/abstract5232.shtml Xu Caijun. Progress of Joint Inversion on Geodesy and Geophysics[J]. Geomatics and Information Science of Wuhan University, 2001, 26(6): 555-561 http://ch.whu.edu.cn/CN/abstract/abstract5232.shtml
[2] 江在森, 张希, 王双绪等.利用地形变观测量求解地壳水平应变场的方法[J].地震, 1999, 19(1):41-48 http://www.cnki.com.cn/Article/CJFDTOTAL-DIZN199901005.htm Jiang Zaisen, Zhang Xi, Wang Shuangxu, et al.The Method of Solving Horizontal Crustal Strain Field by Using Crustal Deformation Observation[J]. Earthquake, 1999, 19(1):41-48 http://www.cnki.com.cn/Article/CJFDTOTAL-DIZN199901005.htm
[3] 李延兴, 胡新康, 帅平, 等.中国大陆地壳水平运动速度场与应变场[J].国际地震动态, 2002(7):1-9 http://www.cnki.com.cn/Article/CJFDTOTAL-GJZT200207000.htm Li Yanxing, Hu Xinkang, Shuai Ping, et al.The Velocity Fields and Strain Fields of Horizontal Crust Motion of the Mainland of China[J]. Recent Developments in World Seismology, 2002, (7): 1-9 http://www.cnki.com.cn/Article/CJFDTOTAL-GJZT200207000.htm
[4] 杨国华, 李延兴, 韩月萍, 等.由GPS观测结果推导中国大陆现今水平应变场[J].地震学报, 2002, 24(4):337-347 http://www.cnki.com.cn/Article/CJFDTOTAL-DZXB200204000.htm Yang Guohua, Li Yanxing, Han Yueping, et al. Current Horizontal Strain Field in Chinese Mainland Derived from GPS Data[J].Acta Seismologica Sinica, 2002, 24(4): 337-347 http://www.cnki.com.cn/Article/CJFDTOTAL-DZXB200204000.htm
[5] 吕江宁, 沈正康, 王敏.川滇地区现代地壳运动速度场和活动块体模型研究[J].地震地质, 2003, 25(4):543-554 http://www.cnki.com.cn/Article/CJFDTOTAL-DZDZ200304002.htm Lü Jiangning, Shen Zhengkang, Wang Min. Contemporary Crustal Deformation and Active Tectonic Block Model of The Sichuan-Yunnan Region, China[J]. Seismology and Geology, 2003, 25(4): 543-554 http://www.cnki.com.cn/Article/CJFDTOTAL-DZDZ200304002.htm
[6] 王晓强, 李杰, Alexander Z, 等.利用GPS形变资料研究天山及邻近地区地壳水平位移与应变特征[J].地震学报, 2007, 29(1):31-37 http://www.cnki.com.cn/Article/CJFDTOTAL-DZXB200701003.htm Wang Xiaoqiang, Li Jie, Alexanderz, et al. Horizontal Movement and Strain Characteristics in Tianshan and Its Adjacent Region with GPS Deformation Data[J].Acta Seismologica Sinica, 2007, 29(1): 31-37 http://www.cnki.com.cn/Article/CJFDTOTAL-DZXB200701003.htm
[7] 王阎昭, 王恩宁, 沈正康, 等.基于GPS资料约束反演川滇地区主要断裂现今活动速率[J].中国科学(D辑), 2008, 38(5):582-597 http://www.cnki.com.cn/Article/CJFDTOTAL-JDXK200805006.htm Wang Yanzhao, Wang Enning, Shen Zhengkang, et al. GPS-constrained Inversion of Present-day Slip Rates along Major Faults of The Sichuan-Yunnan Region, China[J].Science in China Series D: Earth Sciences, 2008, 38(5): 582-597 http://www.cnki.com.cn/Article/CJFDTOTAL-JDXK200805006.htm
[8] 王乐洋.地壳应变参数反演的总体最小二乘方法[J].大地测量与地球动力学, 2013, 33(3):106-110 http://youxian.cnki.com.cn/yxdetail.aspx?filename=WHCH201710017&dbname=CJFDPREP Wang Leyang. Inversion of Crustal Strain Parameters Based on Total Least Squares[J].Journal of Geodesy and Geodynamics, 2013, 33(3): 106-110 http://youxian.cnki.com.cn/yxdetail.aspx?filename=WHCH201710017&dbname=CJFDPREP
[9] Xu P L, Liu J N, Shi C. Total Least Squares Adjustment in Partial Errors-in-variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8):661-675 doi: 10.1007/s00190-012-0552-9
[10] 曾文宪. 系数矩阵误差对EIV模型平差结果的影响研究[D]. 武汉: 武汉大学, 2013 Zeng Wenxian. Effect of the Random Design Matrix on Adjustment of an EIV Model and Its Reliability Theory[D].Wuhan: Wuhan University, 2013
[11] 陶本藻.自由网平差与变形分析[M].武汉:武汉测绘科技大学出版社, 2011 Tao Benzao. Free Network Adjustment and Deformation Analysis[M]. Wuhan: Wuhan Technical University of Surveying and Mapping Press, 2011
[12] Schaffrin B, Felus Y A. On the Multivariate Total Least-squares Approach to Empirical Coordinate[J]. Journal of Geodesy, 2008, 82(6): 373-383 doi: 10.1007/s00190-007-0186-5
[13] 徐锡伟, 闻学泽, 郑荣章, 等.川滇地区活动块体最新构造变动样式及其动力来源[J].中国科学(D辑), 2003, 33(S1): 151-162 http://www.cnki.com.cn/Article/CJFDTOTAL-JDXK2003S1016.htm Xu Xiwei, Wen Xueze, Zheng Rongzhang, et al. Pattern of Latest Tectonic Motion and Its Dynamics for Active Blocks in Sichuan-Yunnan Region, China[J]. Science in China Series D: Earth Sciences, 2003, 33 (Suppl 1): 151-162 http://www.cnki.com.cn/Article/CJFDTOTAL-JDXK2003S1016.htm
[14] Xu C J, Wen Y M. Identification and Analyze of Crustal Motion and Deformation Models in The Sichuan-Yunnan Region[J]. Journal of Applied Geodesy, 2007, 1(4):213-222 http://adsabs.harvard.edu/abs/2007JAGeo...1..213C
[15] Shen Z K, Lv J N, Wang M, et al. Contemporary Crustal Deformation Around The Southeast Borderland of The Tibetan Plateau[J]. Journal of Geophysical Research: Solid Earth, 2005, 110(B11) doi: 10.1029/2004JB003421/suppinfo
[16] 王乐洋. 基于总体最小二乘的大地测量反演理论及应用研究[D]. 武汉: 武汉大学, 2011 Wang Leyang. Research on Theory and Application of Total Least Squares in Geodetic Inversion[D]. Wuhan: Wuhan University, 2011
-
期刊类型引用(4)
1. 王乐洋，邹传义. PEIV模型参数估计理论及其应用研究进展. 武汉大学学报(信息科学版). 2021(09): 1273-1283+1297 . 
百度学术
2. 钟光伟，符平贵，杨钢，张俊. 融合LSC和REHSM的地壳形变分析模型. 矿山测量. 2020(05): 27-30 . 百度学术
3. 韩杰，张松林. 附加一次和二次等式约束的Partial-EIV模型及相应算法. 测绘科学技术学报. 2019(01): 17-22+27 . 百度学术
4. 吕志鹏，隋立芬. 基于非线性高斯-赫尔默特模型的结构总体最小二乘法. 武汉大学学报(信息科学版). 2019(12): 1808-1815 . 百度学术
其他类型引用(3)
计量
- 文章访问数: 1444
- HTML全文浏览量: 267
- PDF下载量: 272
- 被引次数: 7
