-
摘要: 载体运动速度和加速度的精确确定是航空重力中的关键问题之一。基于IGS发布的精密轨道和钟差产品，并对各种相关误差精确模型化，利用载波相位直接法计算速度和加速度。在静态条件下，水平方向的速度精度优于1.5 mm/s，加速度精度优于2.0 mm/s2；垂直方向的速度精度约为2.0 mm/s，加速度精度约为2.5 mm/s2。在动态条件下，与多参考站载波相位直接法精度相当，并且计算效率和解算成功率更高。结果表明了本文方法在航空重力中的有效性。Abstract: Precise velocity and acceleration is one of the key problems in airborne gravimetry. In this paper, a carrier phase-based velocity and acceleration determination method with precise orbit and clock products is introduced. In static case, the horizontal velocity and acceleration are better than 1.5 mm/s and 2.0 mm/s2, respectively, and the vertical ones are about 2.0 mm/s and 2.5 mm/s. In kinematic case, this method is comparable with the multi-reference stations method in precision, and has a higher computational efficiency and success rates. Meanwhile, the sampling rate of precise clock products only influences the velocity, and the order is lower than 1 mm/s. It turns out that the method presented here is effective in airborne gravimetry.
-
Keywords:
- precise ephemeris /
- precise clock /
- carrier phase /
- velocity /
- acceleration
-
悬浮泥沙是湖泊生态系统重要影响因子。一方面，与悬浮泥沙输移有关的冲淤和侵蚀作用过程改变湖盆形态，从而改变其水动力过程，影响湖泊调蓄能力及其湿地水环境与水生态系统[1]；另一方面，悬浮泥沙会使水体浑浊，从而降低水体透光度和改变富氧条件，影响湖泊水生生物的光合作用，加之悬浮泥沙作为污染物的载体，吸附与解吸N、P营养盐与重金属等多种污染物[2]，通过水流作用形成的泥沙输移、再悬浮与沉降，会影响污染物在水体中的迁移转化过程。因此，掌握悬浮泥沙的时空动态是研究湖泊水环境与水生态研究的基础。
鄱阳湖作为长江流域最大的通江淡水湖泊，在调蓄长江洪水和控制长江水质等方面发挥重要作用。受到自然和人为因素的影响，由鄱阳湖浑浊水体悬浮泥沙导致的水环境问题日益突出，悬浮泥沙成为影响鄱阳湖水生态安全的一个重要因子[3]，快速而准确地获取水体悬浮泥沙时空动态信息，对鄱阳湖流域生态环境与经济社会的可持续发展具有重要的意义。
湖泊水动力过程是湖泊水体悬浮泥沙输移扩散的重要因素，因此，利用水力学数值模型一直是研究悬浮泥沙时空动态的重要手段。利用数值模型进行湖泊悬浮泥沙模拟预测研究在国内外也比较广泛[4-7]。国内对于湖泊悬浮泥沙数值模拟的研究起步较晚，如施勇建立洞庭湖泥沙淤积数值模型[8]，对洞庭湖泥沙输移和湖底变形进行了模拟；周杰建立了太湖粘性泥沙输移模型[9]，并利用实测太湖含沙量资料进行了对比分析，结果表明该泥沙模型基本反映了泥沙输运的特点。然而, 利用悬浮泥沙数值模型进行鄱阳湖悬浮泥沙输运的研究目前还没有见诸报道。
数值模拟需要足够的数据进行模型参数率定和结果验证，然而利用现场观测获取这些数据不仅费时费力，而且有限的数据量也无法满足进行数值模拟研究的要求[10]。卫星遥感具有大范围获取水环境真实信息的特点，从而为数值模拟提供了大量的数据源[11]。目前，结合数值模拟和遥感进行悬浮泥沙的研究在国外比较多见，且主要集中在海岸带水环境研究方面[12-14]，国内进行这方面的研究较少。
本文在鄱阳湖水动力模型[10]的基础上进行鄱阳湖泥沙输移过程的数值模拟，利用鄱阳湖底质类型数据辅助对不同底质类型区域上的悬浮泥沙输移数值模型参数进行敏感性分析，基于敏感性分析结果，利用实测站点数据对模型参数进行了分区率定，建立鄱阳湖悬浮泥沙输移模型，并利用该模型进行模拟预测和实测数据的模型验证，最后对比分析了模型模拟和遥感反演的悬浮泥沙空间分布特征，探讨了利用该模型进行鄱阳湖悬浮泥沙时空动态变化研究的可行性。
1 研究区域与数据
1.1 研究区域
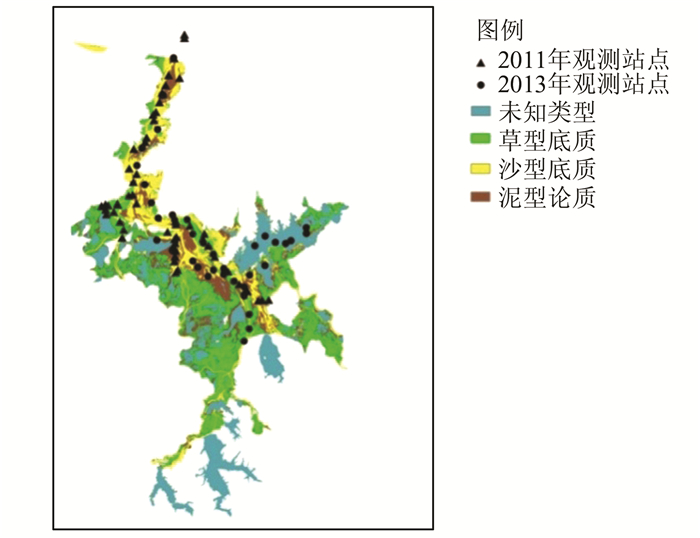
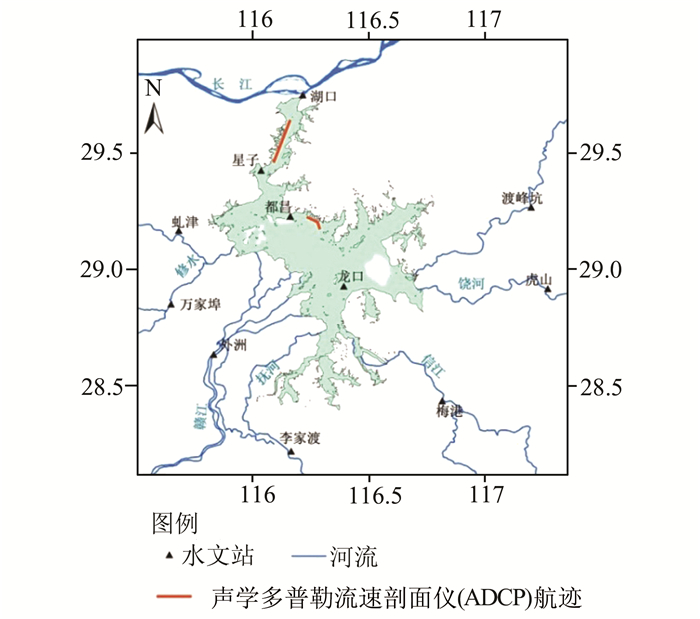
鄱阳湖 (28°22′N~29°45′N、115°47′E~116°45′E) 地处江西省北部，长江中下游南岸 (图 1)，是我国最大的淡水湖泊。鄱阳湖分为南、北两部分，其中南部宽广、较浅，为主湖区；北部狭长、较深，为湖水入长江水道区。鄱阳湖主要接纳赣江、抚河、信江、饶河、修水等五大江河 (以下简称五河) 来水，经调蓄后由湖口汇入长江，鄱阳湖水位随季节的变化明显，是一个过水性、吞吐型的湖泊。
1.2 数据准备
本文对丰水期鄱阳湖水动力和泥沙输移进行数值模拟，模型模拟的时间段为2011-06-01~08-31和2013-06-01~08-31。研究涉及以下4个方面数据。
1) 鄱阳湖及其流域水文数据，包括星子、都昌、康山3个水文站点的逐日水位数据，赣江外洲站、修水虬津站和万家埠站、饶河渡峰坑和虎山站、信江梅港站、抚河李家渡站、湖口站的逐日流量和含沙量数据 (图 1)。
2)2011-07-15~24，对鄱阳湖丰水期湖面进行了8 d的湖泊调查，期间利用走航式ADCP (acoustic Doppler current profilers) 测量了两个断面的流速，分别是都昌附近的断面和入江水道上的断面 (图 1)，同时采集了56个站点的表层水样 (图 2)，利用称重法得到样品的总悬浮泥沙浓度[15]。另外，2013-08-03~08的湖泊调查采集了37个站点的悬浮泥沙浓度数据 (图 2)。
3) 根据鄱阳湖枯水期底质裸露的特点，利用监督分类方法从2009-10-26的鄱阳湖Landsat TM5卫星影像以及2010-12-9的HJ卫星影像得到的鄱阳湖底质类型数据 (图 2)，得到鄱阳湖底质类型有粗沙底质、细泥沙底质、草底质和未知底质区[16]，该数据被用来进行泥沙模型参数敏感性分析和率定。
4) 从国家资源卫星中心下载2011-06-27和2011-07-03 HJ-CCD卫星数据，先后对影像数据进行几何校正和大气校正，利用TSMI遥感反演悬浮泥沙浓度模型[17]，反演得到鄱阳湖悬浮泥沙空间分布数据。
2 研究方法
2.1 模型建立与参数选取
本文基于荷兰Delft University开发的Delft3D-FLOW水流模型建立鄱阳湖水动力与泥沙输移模拟的模型。Delft3D-FLOW建立在Navier-Stokes方程的基础上，采用交替方向法 (alternating direction implicit, ADI) 对控制方程进行离散求解[18]，计算稳定性好且计算速度快。Delft3D-FLOW中包含泥粘性和非粘性泥沙模型模块，一般认为，粘性泥沙包括细颗粒沉积物和粒径小于75 μm的部分[19]。张伟[18]对鄱阳湖总悬浮无粒径分布进行了分析，表明鄱阳湖主要以粒径小于74.48 μm的粘性泥沙为主，因此本研究主要对鄱阳湖粘性泥沙进行模拟。2011-06-01~08-31泥沙模拟过程如下。
1) 利用Dleft3D-RGFGRID工具在模拟区域范围上划分四方形的正交计算网格，网格尺寸大约为200~300 m；利用Delft3D-QUICKIN工具将30 m分辨率的湖底高程数据通过空间差值得到模型计算网格的地形，考虑到一个网格内有多个高程数据点，将网格内所有高程点的高程平均值作为模型计算网格高程；
2) 模拟计算时间步长设置为5 min；由于丰水期鄱阳湖南北湖区水位差异不大，取模拟首日赌场水文站的水位作为模拟的初始水位；使用初始流速和泥沙浓度为0时将模型冷启动。
3) 模型上游边界考虑五河流量和泥沙注入，选取9个河流注入口设置模拟的入湖口，赣江支流4个入湖口 (图 1)，一支在吴城附近流入鄱阳湖入湖流量和泥沙浓度设置为外洲站监测数据的50%，另三支在鄱阳湖西南部流入鄱阳湖，流量分别设置为外洲站监测数据的10%、20%和20%；饶河流经渡峰坑和虎山进入鄱阳湖的两条支流分别设置一个流入口，抚河、信江、修水都设置为一个河流注入口，入湖流量和含沙量分别为各自水文站点的监测值；以湖口附近鄱阳湖流入长江口为开边界，开边界条件为湖口站每日水位。
水动力参数主要包括涡黏性系数和底部糙率系数，涡黏性系数采用文献[20]的研究结果，本文中糙率系数利用实测的流速数据进行率定；粘性泥沙运动主要包括沉降和再悬浮过程，Delft3D中泥沙沉降再悬浮采用Partheniades-Krone的计算方法[21]，主要的参数有泥沙沉降速度、沉降的临界剪切力、底部泥沙侵蚀系数和侵蚀的临界剪切力。经过反复模拟并将模拟结果和实测泥沙浓度进行比较，初步得到空间上一致的泥沙模型参数值 (表 1)，由于改组参数无法足够准确地模拟鄱阳湖悬浮泥沙侵蚀和沉降过程，因此，需要进一步对这些参数进行率定。
表 1 空间上一致的泥沙模型参数Table 1. Spatial-uniform Parameters of Sediment Model参数 参数值 标志 沉降速度/(m·s-1) 1.2×10-4 Ws 沉降的临界剪切力/ (N·m-2) 0.01 TauD 侵蚀的临界剪切力/(N·m-2) 0.06 TauE 侵蚀系数/(kg·(m-2·s-1)) 4×10-7 E0 2.2 泥沙模型参数敏感性分析与率定
鄱阳湖不同区域上底质类型不同会导致不同区域上泥沙再悬浮和沉降过程的差异，同时考虑空间分布上一致的泥沙模型参数无法准确地模拟鄱阳湖的泥沙输移过程，本研究使用空间上不一致的泥沙模型参数进行鄱阳湖泥沙的数值模拟。为了更好地分区率定得到空间上不一致的泥沙模型参数，本研究利用鄱阳湖底质类型数据辅助进行不同底质区域上泥沙模型参数的敏感性。
常规的敏感性分析采用一次一个变量法，即每次只变动一个参数，而保持其他参数不变来运行模型，从而判断其对模型结果输出的影响。利用该方法敏感性计算如下：
(1) 式中, F(x) 为在参考参数x下的泥沙模拟结果；F(x+50%) 表示参考参数增加50%后的泥沙模拟结果；Si为泥沙浓度对参数变化表现出的敏感性，Si越大，就代表参数x模型影响越大。本研究泥沙模型中泥沙沉降速度、沉降的临界剪切力、底部泥沙侵蚀系数和侵蚀的临界剪切力参考参数适用表 1的结构，考虑到单个网格位置上的泥沙模型参数敏感性不足以代表某个底质类型区域上泥沙模型参数敏感性，因此，本文将某一底质类型的模拟空间区域上选取均匀分布的100个网格点的平均敏感度作为该底质类型的泥沙模型参数敏感度。
(2) 式中，平均敏感性Sa就代表该底质类型的模拟区域对参考参数x的敏感性程度。基于不同区域上各泥沙模型参数的敏感性分析结果，针对不同底质区域按参数敏感性程度手动调整泥沙模型参数，将模拟结果和和对应底质区上的实测数据进行比较，从而得到不同底质区上合适的空间上不一致的泥沙模型参数。
3 结果与讨论
3.1 水动力模型参数率定与验证
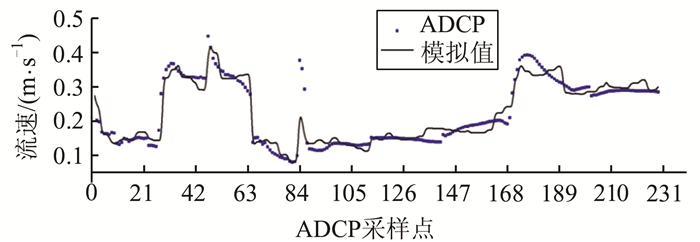
利用ADCP测量流速数据对底部糙率进行手动率定，选取一个最优的糙率值，结果表明，当底部糙率为0.026时，模拟结果的均方根误差最小。图 3是糙率为0.026时模拟流苏大小和ADCP实测流速数据的比较图。模拟的流速能较好地拟合实测流速，模拟流速平均相对误差为9.3%，相关系数平方达到0.91。可以看到较个别数据采集点位置ADCP测量流速较模拟结果偏大很多，可能原因是ADCP航迹在航道附近，受航道上船只航行造成的波流的影响，ADCP测量流速数据突然变大。
![]()
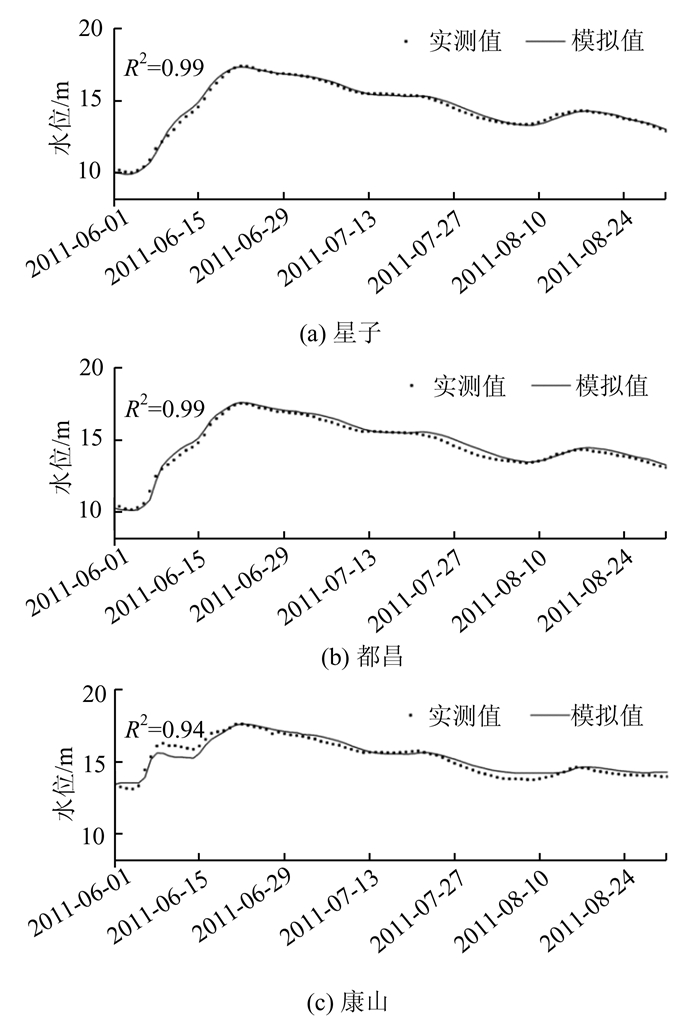
图 3 模拟和ADCP测量的流速比较Figure 3. Comparison of the Simulated and the ADCP Measured Velocity将鄱阳湖湖区星子、都昌、康山等3个水文站实测水位数据和模拟的水位进行对比 (图 4)，可以看到模拟水位与实测结果有很好的一致性，3个水位站模拟水位的平均相对误差分别为1.0%、1.4%、1.7%，与实测水位的R2分别为0.99、0.99、0.94。总的来说，该模型能很好地模拟鄱阳湖丰水期水动力变化。
![]()
图 4 模拟和水文站点测量的水位比较Figure 4. Comparison of Water Level from the Simulated and Hydrological Stations3.2 泥沙模型参数敏感性
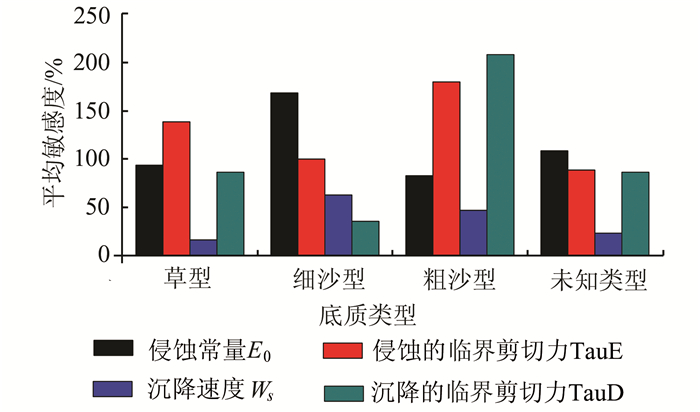
利用变化其中一个泥沙模型参数进行参数敏感性分析，得到不同底质区4个参数的敏感性分析比较，如图 5所示。从图 5可以看出，各类型底质区上泥沙模型各参数的敏感性有较明显的差异，导致这种差异的原因是不同底质对底部泥沙再悬浮和泥沙沉降的作用能力各不相同。对于草型底质区中，泥沙模拟对侵蚀的临界剪切力的敏感性最高；其次是侵蚀常量，敏感性最小的是泥沙沉降速度，草型底质对底部侵蚀的阻碍较大，底部泥沙再悬浮能力较弱。因此，对存在该底质的区域对侵蚀过程的参数更加敏感；细沙型底质区域中，泥沙模拟对侵蚀常量的敏感性最高，这是因为底部细沙更容易再悬浮；粗砂型底质区域泥沙模拟敏感性最高的是泥沙沉降的临界剪切力，其次是泥沙侵蚀的临界剪切力，可能原因是该类底质区域中较粗颗粒的泥沙侵蚀再悬浮后，由于泥沙粒径较大，泥沙也更容易沉降到底部；对于未知底质类型区域，各个参数的敏感性的高低与草型底质有较大的相似，可以推测未知底质类型区域可能含有大量的水草。鄱阳湖各个底质类型区域泥沙模拟对侵蚀过程中的模型参数敏感性高于沉降过程中泥沙模型参数的敏感性。
![]()
图 5 不同底质区域对泥沙模型参数的敏感性Figure 5. Parameter Sensitivities of Sediment Transport Model with Different Lake Substrates3.3 泥沙模型参数分区率定
由于不同底质区域上模型参数对模拟结果影响的不同，本研究考虑采用使用空间上不一致的模型参数进行泥沙的模拟，从而更加准确地模拟鄱阳湖悬浮泥沙的时空动态变化。根据不同底质类型区上泥沙模型参数敏感性分析结果，利用位于不同底质区上的实测泥沙数据，每一类底质区手动进行参数率定。以草型底质区参数率定为例，考虑到草型底质区泥沙侵蚀 (再悬浮) 的临界剪切力最敏感，首先考虑调整该参数来调整模拟结果，由于底部侵蚀的临界剪切力越大，再悬浮的泥沙量越少，悬浮泥沙浓度越低，因而在率定过程中考虑将该参数调大，降低模拟的悬浮泥沙浓度值，使模拟结果与实测值接近。表 2是分区率定的结果，从表中可以看出，草型底质区临界剪切力从0.06 N/m2调整为0.3 N/m2，变化幅度较大。为了取得更好的模拟结果，使模拟结果相对于实测数据的误差进一步减小，需要在此基础上微调其他次级敏感参数，因此，对侵蚀常量和沉降的临界剪切力进行了微调。参数率定后，草型底质区上站点模拟结果均方根误差为24.5 mg/L，误差减少了79.6%，同样针对细沙和粗砂底质类型区域，使用类似的过程对这些区域上的模型参数进行率定。表 2给出了不同底质区域上的泥沙模拟参数率定后最终的参数的取值。由于未知底质类型的区域上没有实测站点的数据，因而无法利用参数率定确定该类底质区域上泥沙模型参数，考虑到未知底质类型上各参数的敏感性和草型底质类型上各参数的敏感性相近，因此，在模型中未知底质类型区域使用与草型底质类型相同的泥沙模拟参数。
表 2 基于敏感性分析结果的不同底质区域参数率定结果Table 2. Parameters of Sediment Transport Model in Different Substrate Type Area Based on Sensitivity Analysis Results底质类型 泥沙侵蚀的参数 泥沙沉降的参数 侵蚀常量
E0/(kg·(m-2·s-1))侵蚀的临界剪切力
TauE/(N·m-2)沉降速度
Ws/(m·s-1)沉降的临界剪切力
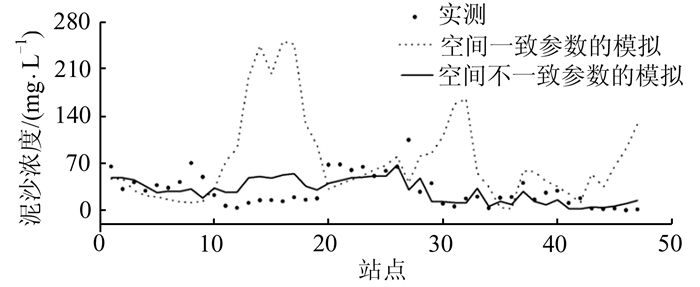
TauD/(N·m-2)草 2×10-7 0.3 1.2×10-4 0.02 细沙 6×10-7 0.06 1.2×10-4 0.01 粗砂 4×10-7 0.04 2.0×10-4 0.005 未知 2×10-7 0.3 1.2×10-4 0.02 使用表 2中空间上不一致的模型参数进行模拟，使用表 1中空间一致的模型参数模拟结果与实测值进行对比，如图 6所示，使用空间一致和空间不一致泥沙模型参数的模拟结果差异较大，特别是位于草型底质区的站点上 (图 6中站点编号10~20之间)，这些站点上使用空间一致的模型参数悬浮泥沙模拟结果异常大，参数率后模拟结果大幅度变小，且更接近实测的悬浮泥沙浓度。这是由于使用空间上不一致的参数，对草型底质类型区域上泥沙模型参数进行单独率定后，草型区域上泥沙侵蚀常量变小，而泥沙侵蚀的临界剪切力变大，从而使得草型底质区域泥沙再悬浮的能力减弱，模拟得到的悬浮泥沙浓度变小而更接近实测的泥沙浓度。总之，使用空间不一致的泥沙模型参数考虑了不同底质区域上泥沙沉降和再悬浮过程的差异，通过参数分区率定得到空间不一致的的模型参数模拟的悬浮泥沙浓度能更好地拟合实测值。参数分区率定后，相对于实测结果，模拟的泥沙浓度均方根误差为21.6 mg/L，相对于参数率定前使用空间一致的模型参数模拟的结果，均方根误差减少86.2%。因此，研究表明分区率定得到的泥沙模型参数满足鄱阳湖悬浮泥沙模拟的要求。
![]()
图 6 空间一致和空间不一致参数泥沙模拟结果比较Figure 6. Comparison of Sediment from the Model with Spatial-uniform Parameters, Spatial-different Parameters, and the Insitu Measurements3.4 模型预测结果的验证
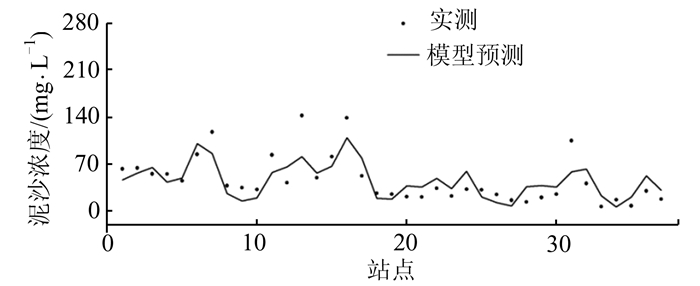
为了进一步验证模型的有效性，对2013年丰水期6~8月的悬浮泥沙输移过程进行模拟预测，并用2013年8月份湖区调查实测的悬浮泥沙浓度对预测结果的有效性进行验证。图 7为实测和模型预测结果的对比，可以看到预测的悬浮泥沙浓度和实测的泥沙浓度具有较好的一致性，预测的泥沙浓度均方根误差为19.8 mg/L，相关系数R2为0.78。从图 7可以看到，某些站点泥沙模拟结果明显低于实测的泥沙浓度，这是因为这些站点位于鄱阳湖采砂区附近，采砂活动导致底部泥沙大量的再悬浮，进而扩散到附近水域，因此导致实测泥沙浓度较大。本研究的悬浮泥沙输移模型能够合理地进行鄱阳湖悬浮泥沙输移过程预报。
![]()
图 7 2013年泥模型预测结果验证Figure 7. Validation of Predicted Results of Sediment Transport Model in 20133.5 模拟和遥感反演的悬浮泥沙空间的对比
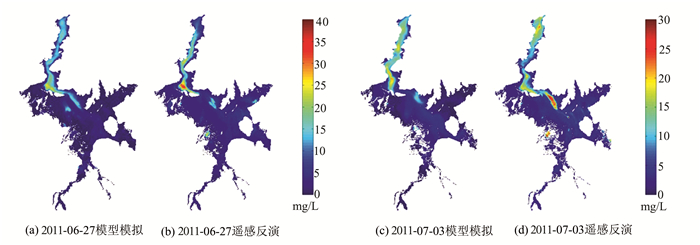
遥感对地观测是对地表水质进行间接观测的一种方式，遥感水环境监测有着其真实可靠的特点，能够很好地表现水坏境要素的空间分布状态。为了进一步证实本研究建立的泥沙输移数值模型模拟预测鄱阳湖悬浮泥沙的可靠性，本研究利用遥感反演的悬浮泥沙浓度空间分布数据。图 8是遥感反演的2011-06-27和07-03悬浮泥沙空间分布和对应时间点模拟的悬浮泥沙空间分布，可以看到，在整体上模型模拟和遥感监测到的悬浮泥沙分布特征在空间上相近，都表现为北部入江水道和南部湖区悬浮泥沙浓度较高，泥沙浓度在20 mg/L左右；而南部湖区泥沙浓度较低，泥沙浓度在5 mg/L左右，可以认为模型结果与遥感反演结果具有较好的空间一致性。因此，该模型能够模拟预测得到满意的鄱阳湖悬浮泥沙空间分布状态。图 8中，在2011-06-27和2011-07-03两个相近的时间点，模拟得到的悬浮泥沙空间分布有一定的差异，这说明该模型具有模拟鄱阳湖悬浮泥沙时间动态变化的能力，因此，利用该模型进行鄱阳湖悬浮泥沙时空动态变化特征及其影响机制的研究，将是一个十分有用的工具。
![]()
图 8 模型模拟和遥感反演的悬浮泥沙空间分布比较Figure 8. Comparison of Spatial Distribution of Sediment Concentration from the Model and Remote Sensing Images4 结论与展望
本研究针对丰水期鄱阳湖，充分利用遥感数据辅助进行了鄱阳湖悬浮泥沙浓度遥感的模拟预测。
1) 利用遥感监测的鄱阳湖底质类型数据进行了悬浮泥沙模型参数敏感性分析，研究表明，鄱阳湖不同底质的区域上泥沙模型参数具有较大的空间差异；
2) 基于敏感性分析结果，对鄱阳湖不同区域上的泥沙模型参数进行了分区率定。实测悬浮泥沙浓度数据验证表明，利用分区率定得到的模型参数能够较好地模拟预测鄱阳湖悬浮泥沙输移过程。
3) 将模型模拟和遥感反演的悬浮泥沙浓度空间分布进行了比较，两者具有很好的空间分布一致性，表明该模型能够模拟预测鄱阳湖悬浮泥沙的时空动态变化。
本研究结合数值模拟和遥感为湖泊水环境的模拟预测提供了有效的方法，同时建立的模型为研究鄱阳湖水环境时空动态变化特征及其影响机制打下了坚实的基础。进一步的研究还可以利用类似方法建立鄱阳湖三维悬浮泥沙输移模型，在泥沙模型的基础上加入水质要素的模拟，分析悬浮泥沙影响下鄱阳湖水质要素空间动态变化机制；另外，利用模型模拟和遥感反演悬浮泥沙的误差信息，并同时利用数据同化方法，进一步提高鄱阳湖悬浮泥沙时空动态变化模拟预测的能力。
-
![]()
图 1 动态实验速度和加速度结果比较
Figure 1. Comparison of Velocity and Acceleration in Kinematic Test
表 1 静态实验速度和加速度结果统计
Table 1 Statistics of Velocity and Acceleration in Static Test
速度/(mm\5s-1) 加速度/(mm\5s-2) N E U N E U 均值 PPVA -0.026 9 0.008 2 -0.026 9 -0.004 3 0.005 0 -0.004 0 EVA -0.020 1 0.020 1 -0.007 8 -0.002 7 0.005 6 -0.006 3 RMS PPVA 0.908 1 1.305 1 2.044 2 1.232 9 1.701 8 2.491 5 EVA 0.950 2 1.294 5 1.672 7 1.348 6 1.835 8 2.365 4 
下载: 导出CSV
表 2 静态实验加速度结果统计/mGal
Table 2 Statistics of Acceleration in Static Test/mGal
30 s 60 s 90 s 120 s 均值 RMS 均值 RMS 均值 RMS 均值 RMS U 0.03 7.4 0.03 2.6 0.02 1.50 0.02 1.22 PPVA E 0.58 3.9 0.56 1.6 0.54 1.09 0.49 0.98 N -0.22 2.4 -0.21 0.9 -0.20 0.59 -0.18 0.51 U 0.62 3.7 -0.60 2.1 -0.57 1.44 0.52 1.23 EVA E 0.56 3.5 0.54 1.8 0.51 1.21 0.46 1.04 N -0.27 2.2 -0.26 1.1 -0.24 0.79 -0.22 0.71
下载: 导出CSV
表 3 选择不同参考站的解算成功率统计
Table 3 Statistics of Success Rate with Different Reference Stations
参考站 参考站的选择 MSSC 0009 BVHS BVHS和0009 MSSC和BVHS MSSC和0009 MSSC、BVHS和0009 解算成功率/% 92.5 94.9 94.9 94.0 91.7 91.7 90.8
下载: 导出CSV
表 4 动态实验速度和加速度差分结果统计
Table 4 Statistics of Velocity and Acceleration Difference in Kinematic Test
速度/(mm\5s-1) 加速度/(mm\5s-2) N E U N E U 均值 0.014 0 -0.055 6 0.019 7 -0.002 5 -0.000 5 -0.001 5 标准差 1.307 0 1.432 6 3.272 8 1.656 8 1.797 9 4.011 3
下载: 导出CSV
表 5 动态实验加速度差值统计/mGal
Table 5 Statistics of Acceleration Difference in Kinematic Test/mGal
30 s 60 s 90 s 120 s 均值 标准差 均值 标准差 均值 标准差 均值 标准差 U -0.15 9.48 -0.15 4.14 -0.15 2.90 -0.14 2.63 E -0.05 4.79 -0.05 2.13 -0.05 1.44 -0.05 1.29 N -0.25 4.33 -0.25 1.75 -0.25 1.19 -0.24 1.07
下载: 导出CSV
-
[1] Bruton A M. Improving the Accuracy and Resolution of SINS/DGPS Airborne Gravimetry[D]. Calgary: The University of Calgary, 2000 http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.33.2681
[2] 张开东.基于SINS/DGPS的航空重力测量方法研究[D].长沙:国防科技大学, 2007 http://cdmd.cnki.com.cn/Article/CDMD-90002-2008098727.htm Zhang Kaidong. Research on the Method of Airborne Gravimetry Based on SINS/DGPS[D]. Changsha: National University of Defense Technology, 2007 http://cdmd.cnki.com.cn/Article/CDMD-90002-2008098727.htm
[3] Bruton A M, Glennie C L, Schwarz K P. Differentiation for High-percision GPS Velocity and Acceleration Determination[J].GPS Solutions, 1999, 2(4): 7-21 doi: 10.1007/PL00012771
[4] Jekeli C. On the Computation of Vehicle Accelerations Using GPS Phase Accelerations[C].The International Symposium on Kinematic Systems in Geodesy, Geomatics and Navigation (KIS94), Banff, Canada, 1994
[5] Jekeli C, Garcia R. GPS Phase Accelerations for Moving-base Vector Gravimetry[J].Journal of Geodesy, 1997, 71(10): 630-639 doi: 10.1007/s001900050130
[6] Kennedy S. Acceleration Estimation from GPS Carrier Phases for Airborne Gravimetry[D]. Calgary: The University of Calgary, 2002
[7] Salazar D, Hernandez-Pajares M, Juan J, et al. EVA: GPS-based Extended Velocity and Acceleration Determination[J].Journal of Geodesy, 2011, 85(12): 329-340
[8] 肖云, 夏哲仁.航空重力测量中载体运动加速度的确定[J].地球物理学报, 2003, 46(1): 62-67 http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200301010.htm Xiao Yun, Xia Zheren. Determination of Moving-Base Acceleration in Airborne Gravimetry[J].Chinese Journal of Geophysics, 2003, 46(1): 62-67 http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200301010.htm
[9] Salazar D, Hernandez-Pajares M, Juan J, et al. Network-based High Accuracy Positioning with the GPSTk[C]. The 5th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVI TEC' 2010), Noordwijk, Netherlands, 2010
[10] Zhang Jianjun. Precise Velocity and Acceleration Determination Using a Standalone GPS Receiver in Real Time[D]. Melbourne: Royal Melbourne Institute of Technology, 2007 https://researchbank.rmit.edu.au/view/rmit:9492
[11] Kouba J.A Guide to Using International GNSS Service (IGS) Products[OL]. http//igscb.jpl.nasa.gov/igscb/resource/pubs/UsingIGSProductsVer21.pdf,2011
[12] 王甫红, 张小红, 黄劲松. GPS单点测速的误差分析及精度评价[J].武汉大学学报·信息科学版, 2007, 32(6): 515-519 http://ch.whu.edu.cn/CN/Y2007/V32/I6/515 Wang Fuhong, Zhang Xiaohong, Huang Jinsong. Error Analysis and Accuracy Assessment of GPS Absolute Velocity Determination with SA off[J].Geomatics and Information Science of Wuhan University, 2007, 32(6):515-519 http://ch.whu.edu.cn/CN/Y2007/V32/I6/515
-
期刊类型引用(0)
其他类型引用(3)
计量
- 文章访问数: 1536
- HTML全文浏览量: 193
- PDF下载量: 397
- 被引次数: 3
