利用光学遥感影像光流场模型进行地表形变分析

丁明涛; 陈浩杰; 李振洪; 刘振江

doi:10.13203/j.whugis20240071

利用光学遥感影像光流场模型进行地表形变分析

丁明涛^{1, 2, 3, 4, 5,},
陈浩杰^{1, 2, 3},
李振洪^{1, 2, 3, 4, ,},
刘振江^{1, 2, 3}

1.
长安大学地质工程与测绘学院,陕西西安,710054
2.
黄土科学全国重点实验室,陕西西安,710054
3.
长安大学地学与卫星大数据研究中心,陕西西安,710054
4.
自然资源部生态地质与灾害防控重点实验室,陕西西安,710054
5.
智慧地球重点实验室,北京,100029

基金项目:

国家重点研发计划 2021YFC300400

国家自然科学基金 42374027

陕西省科技创新团队 2021TD-51

陕西省地学大数据与地质灾害防治创新团队（2022）

智慧地球重点实验室基金 KF2023YB04-01

高分专项川藏区域综合治理应用与规模化产业化示范项目 87-Y50G28-9001-22/23

中央高校基本科研业务费专项资金 300102262203

中央高校基本科研业务费专项资金 300102262902

详细信息

作者简介:
丁明涛,博士,副教授,主要从事机器学习、遥感影像处理研究。mingatoding@chd.edu.cn

通讯作者:
李振洪,博士,教授。zhenhong.li@chd.edu.cn

计量
- 文章访问数: 452
- HTML全文浏览量: 107
- PDF下载量: 159
出版历程
- 收稿日期: 2024-02-29
- 网络出版日期: 2024-05-30
- 刊出日期: 2024-08-04

Analysis of Surface Deformations on the Basis of Optical Flow Field Models from Optical Remote Sensing Images

DING Mingtao^{1, 2, 3, 4, 5,},
CHEN Haojie^{1, 2, 3},
LI Zhenhong^{1, 2, 3, 4, ,},
LIU Zhenjiang^{1, 2, 3}

1.
College of Geological Engineering and Geomatics, Chang'an University, Xi'an710054, China
2.
Key Laboratory of Loess, Xi'an710054, China
3.
Big Data Center for Geosciences and Satellites, Xi'an710054, China
4.
Key Laboratory of Ecological Geology and Disaster Prevention, Ministry of Natural Resources, Xi'an710054, China
5.
Laboratory of Smart Earth, Beijing100029, China

摘要

摘要:
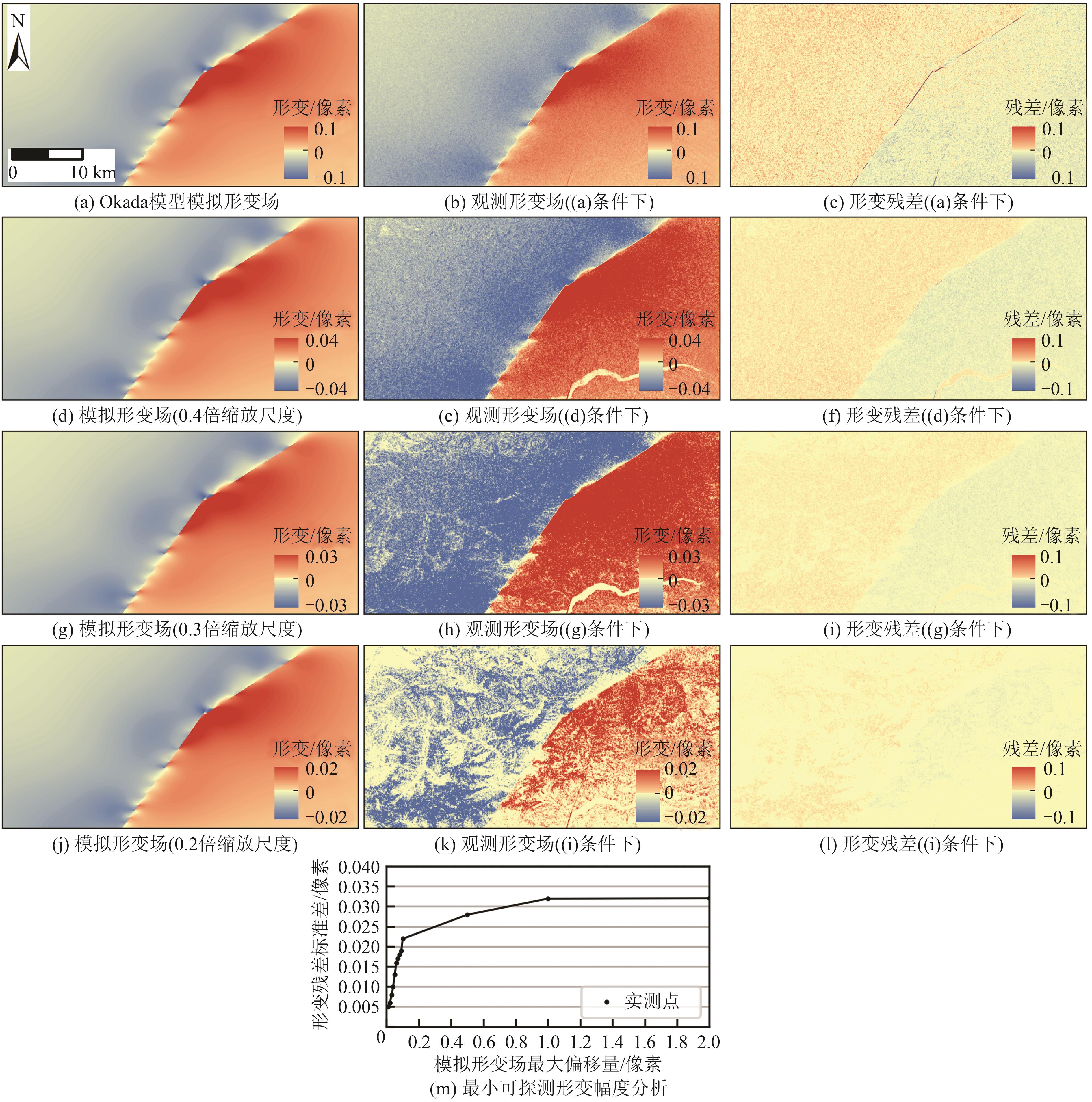
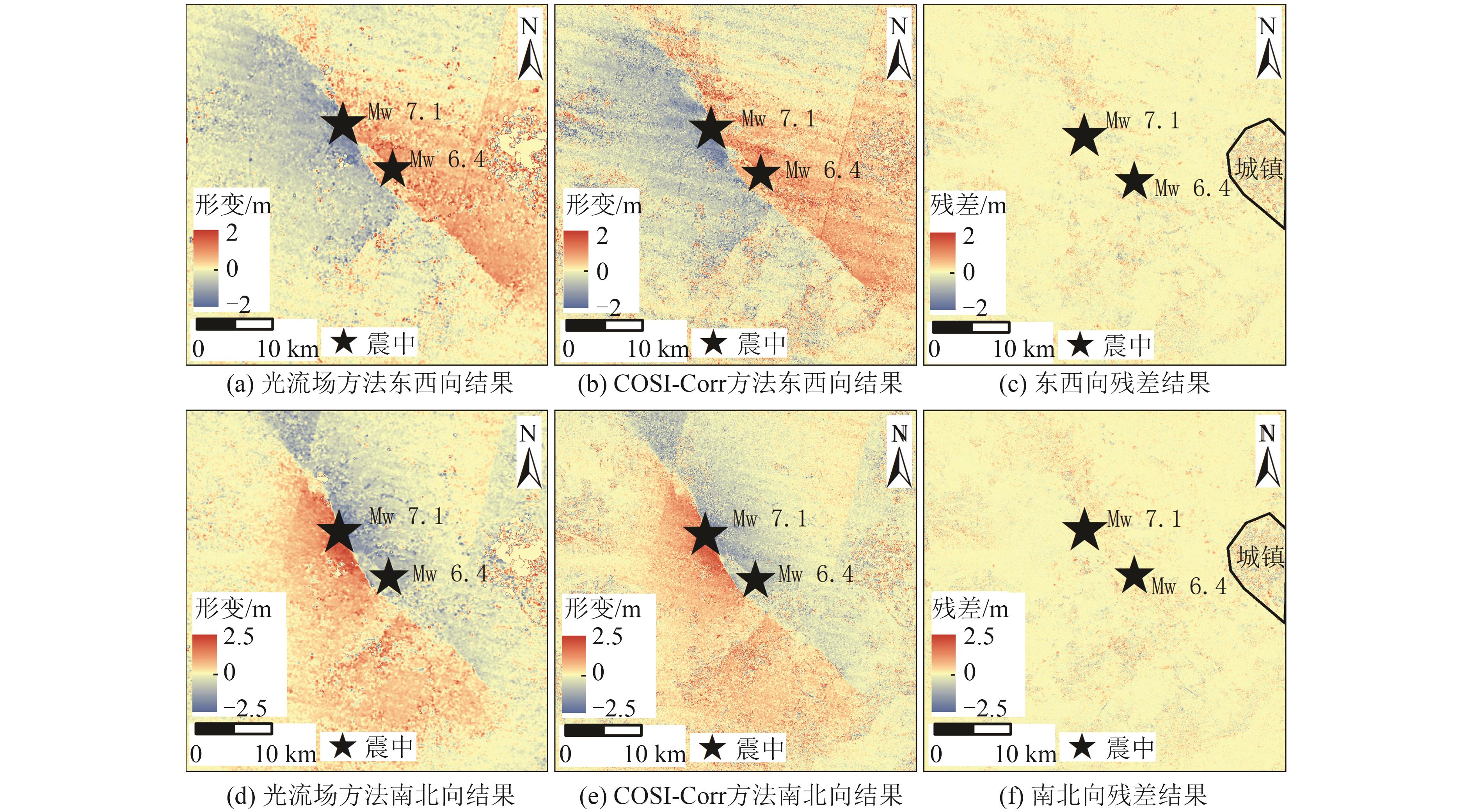
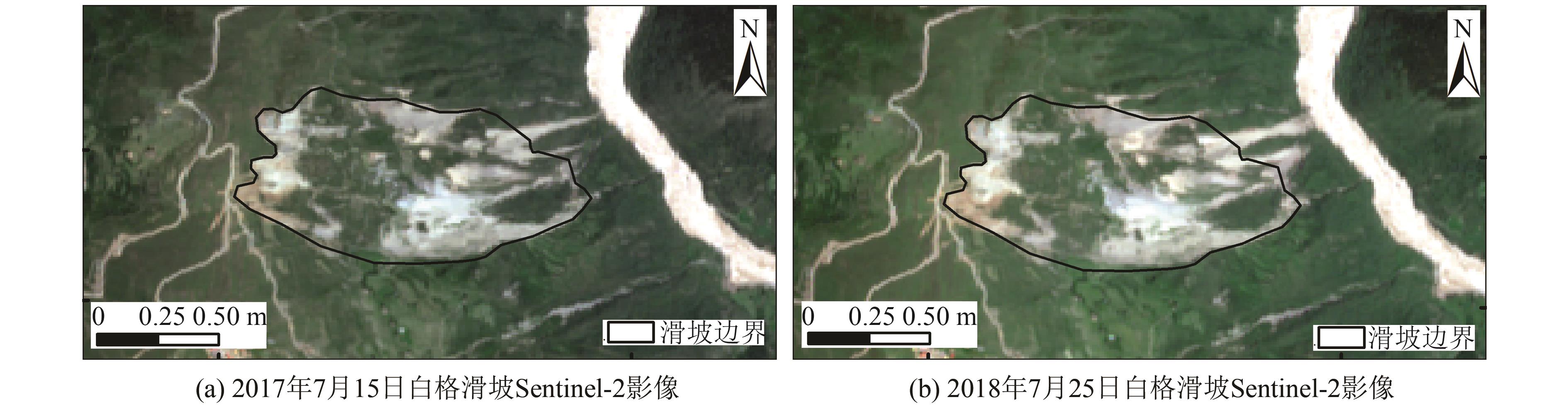
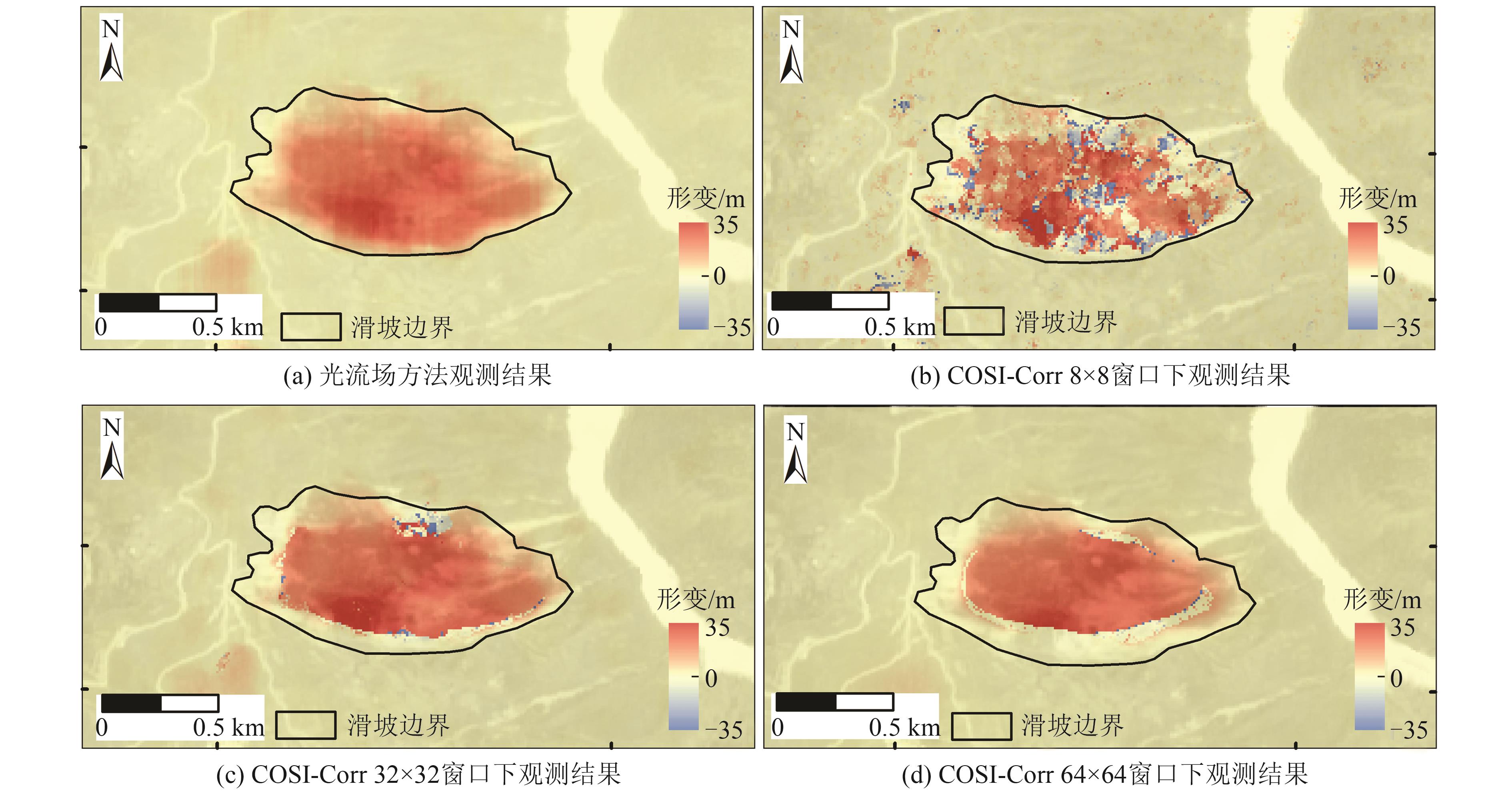
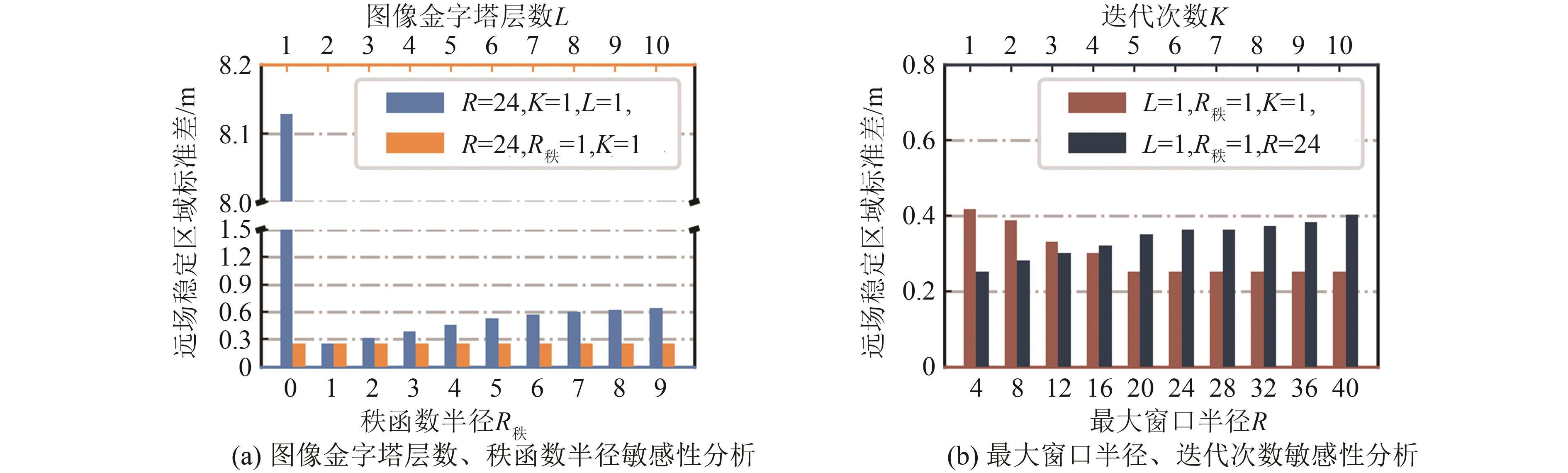
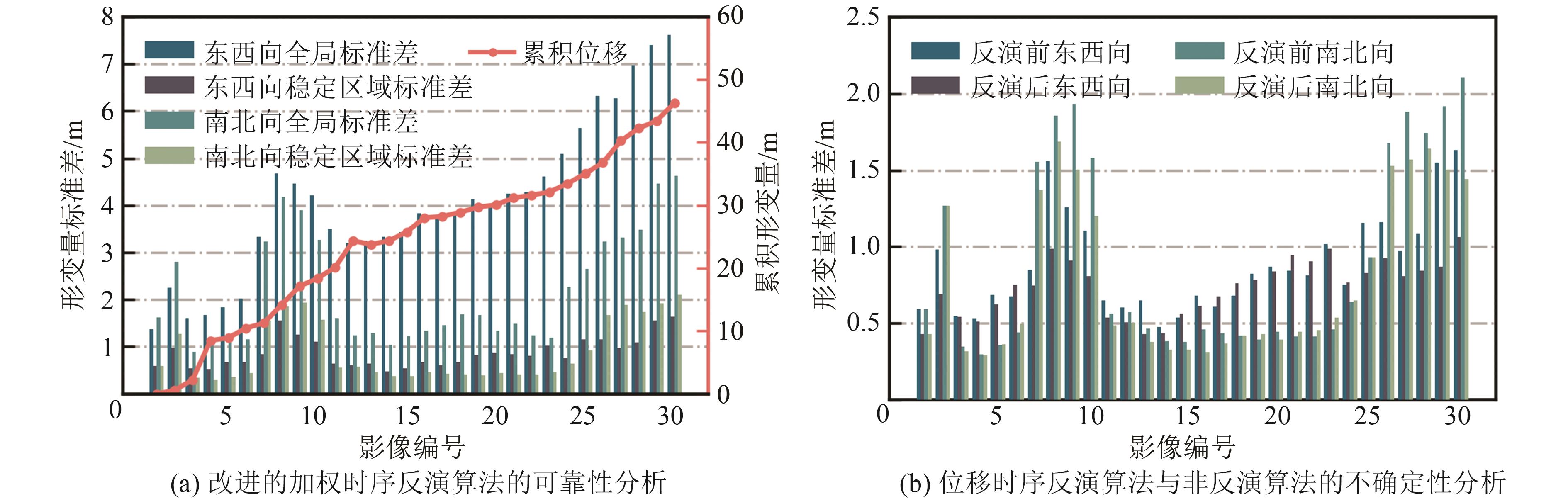
光学遥感影像像素偏移量追踪是反演同震形变场和监测滑坡的一种重要手段。基于相关性匹配的传统像素偏移量追踪方法,通过搜索相关性最强的匹配窗口估计中心像素的位移,计算效率低且在大梯度形变区域失相关现象严重,存在形变边界提取不精确的问题。为高效获取精确的地表形变,将计算机视觉领域的光流场模型引入像素偏移量追踪问题,提出适用于光学遥感影像反演地表形变的光流场方法,给出像素偏移量时序反演的加权改进算法。通过塔吉克斯坦同震形变场模拟实验,评估光流场方法估计地表形变场的可行性及其在最小可探测形变方面的性能；通过加州地震同震形变场反演和白格滑坡偏移量估计实验,讨论光流场方法的计算效率优势和形变区域提取的精确性；通过白格滑坡时序形变分析,进一步论述利用光流场方法估计大梯度形变的有效性和时序反演加权改进算法的鲁棒性。结果显示,相比于传统窗口相关性匹配方法,光流场方法的偏移量追踪精度为0.032像素,计算效率提升了20倍左右,形变区范围提取精度提升了25.9%；改进的加权时序反演算法将光学遥感影像东西向和南北向位移估计的不确定性分别降低了16.2％和12.4％。
- 光流场方法 /
- 滑坡 /
- 同震形变 /
- 计算效率 /
- 加权时序反演算法
Abstract:
Objectives
Pixel offset tracking (POT) for optical remote sensing imagery is widely used to invert coseismic deformation fields and monitor landslides. Traditional pixel offset tracking method estimates the displacement of the central pixel by searching for the matching window with the highest correlation, which is computationally inefficient and suffers from inaccurate deformation boundary extraction due to the decoherence effects in the region with dynamical deformation. We introduce the optical flow field model commonly used in computer vision to the pixel offset tracking problem to obtain accurate surface deformation efficiently.
Methods
The optical flow field method applicable to optical remote sensing images and the improved inversion algorithm for the time series analysis are proposed to inverse the surface deformation. Experiments on the simulated coseismic deformation fields in Tajikistan are detailed to assess the feasibility and the minimum detectable deformation of the optical flow field method. The advantages of the proposed method over computational cost and deformation boundary extraction accuracy are illustrated by the co-seismic deformation field of the California earthquake and the displacement of the Baige landslide. Furthermore, the performance on estimating large gradient deformation and the robustness of the improved time series inversion algorithm are discussed by analyzing the time series deformation of the Baige landslide.
Results
The results show that compared with the traditional window correlation matching method, the optical flow field method has an offset tracking accuracy of 0.032 pixel, which improves the computational efficiency by about 20 times, and the accuracy of the deformation zone is improved by 25.9%. The time series weighted inversion algorithm reduces the uncertainties in the estimation of east-west and north-south displacements of optical remote sensing images by 16.2% and 12.4%, respectively.
Conclusions
The proposed method alleviates the pixel offset tracking problem in the boundary region with large gradient deformation.
- optical flow field method /
- landslides /
- coseismic deformation /
- computational efficiency /
- weighted time series inversion algorithm
http://ch.whu.edu.cn/cn/article/doi/10.13203/j.whugis20240071

HTML全文

http://ch.whu.edu.cn/cn/article/doi/10.13203/j.whugis20240071

图 1 光流场方法地表形变分析流程

Figure 1. Analysis Process of Surface Deformation Based on Optical Flow Field Model

下载: 全尺寸图片幻灯片

图 2 光流场模型

Figure 2. Optical Flow Field Model

下载: 全尺寸图片幻灯片

图 3 2015⁃12⁃05塔吉克斯坦Sentinel-2影像及模拟震后影像

Figure 3. Sentinel-2 Image of Takixtan on December 5, 2015 and Simulated Post-Earthquake Image

下载: 全尺寸图片幻灯片

图 4 模拟形变场、光流场方法观测结果、形变残差及最小可探测形变幅度分析

Figure 4. Simulated Deformation Fields, Observations Based on Optical Flow Field Methods, Analysis of Deformation Residuals and Minimum Detectable Deformation Amplitude

下载: 全尺寸图片幻灯片

图 5 南加州区域里奇克雷斯特地震发生前后Sentinel-2影像

Figure 5. Sentinel-2 Images Taken Before and After the Ridgecrest Earthquake in the Southern California

下载: 全尺寸图片幻灯片

图 6 光流场方法观测结果与COSI-Corr方法观测结果对比分析

Figure 6. Comparative Analysis of Observation Results of Optical Flow Field Method and COSI-Corr Method

下载: 全尺寸图片幻灯片

图 7 光流场方法观测结果与COSI-Corr方法观测结果线性拟合散点密度图

Figure 7. Scatter Diagram of Linear Fitting Between Optical Flow Field Observation Results and COSI-Corr Observation Results

下载: 全尺寸图片幻灯片

图 8 白格滑坡灾前不同时期的Sentinel-2影像

Figure 8. Sentinel-2 Images Taken at Different Times Before the Baige Landslide Disaster

下载: 全尺寸图片幻灯片

图 9 光流场方法观测结果与COSI-Corr方法观测结果定性对比

Figure 9. Qualitative Comparison of Optical Flow Field Method Observations with COSI-Corr Method Observations

下载: 全尺寸图片幻灯片

图 10 白格滑坡区域概况及其垮塌前后Sentinel-2影像

Figure 10. Regional Overview of the Baige Landslide and the Sentinel-2 Images Taken Before and After the Collapse

下载: 全尺寸图片幻灯片

图 11 白格滑坡位移时间序列及特征点累计形变、滑移速率

Figure 11. Time Series of the Displacement of the Baige Landslide as well as the Cumulative Deformation and the Slip Rates at the Feature Points

下载: 全尺寸图片幻灯片

图 12 光流场方法最佳参数选择

Figure 12. Optimal Parameter Selection for Optical Flow Field Method

下载: 全尺寸图片幻灯片

图 13 改进加权时序反演算法的可靠性及有效性分析

Figure 13. Reliability and Validity Analysis of Improved Weighted Time Series Inversion Algorithm

下载: 全尺寸图片幻灯片

表 1 Sentinel-2影像参数

Table 1 Parameters of Sentinel-2 Images

影像编号	采集时间	季节	影像编号	采集时间	季节
0	2015-11-13	冬季	16	2017-12-02	冬季
1	2015-12-23	冬季	17	2017-12-07	冬季
2	2016-05-11	春季	18	2017-12-17	冬季
3	2016-11-07	秋季	19	2017-12-22	冬季
4	2016-12-07	冬季	20	2018-01-11	冬季
5	2017-01-16	冬季	21	2018-01-16	冬季
6	2017-02-05	冬季	22	2018-01-26	冬季
7	2017-05-16	春季	23	2018-02-05	冬季
8	2017-07-15	夏季	24	2018-03-22	春季
9	2017-08-04	夏季	25	2018-04-16	春季
10	2017-08-24	夏季	26	2018-05-21	春季
11	2017-10-18	秋季	27	2018-06-05	夏季
12	2017-10-28	秋季	28	2018-06-10	夏季
13	2017-11-07	秋季	29	2018-06-25	夏季
14	2017-11-17	秋季	30	2018-07-25	夏季
15	2017-11-27	秋季

下载: 导出CSV

表 2 Sentinel-2不同波段稳定区域标准差比较

Table 2 Comparison of Standard Deviations of Sentinel-2 in Different Wavebands

影像对	方向	标准差/m
影像对	方向	蓝色波段	绿色波段	红色波段	近红外波段	SR波段	灰度波段
2017-07-15—2018-07-25	东西向	0.675	0.429	0.372	1.109	0.597	0.361
2017-07-15—2018-07-25	南北向	0.543	0.496	0.445	0.834	0.864	0.436
2015-11-13—2016-11-07	东西向	0.673	0.563	0.571	1.488	0.614	0.531
2015-11-13—2016-11-07	南北向	0.393	0.258	0.295	0.813	0.421	0.213

下载: 导出CSV

表 3 加州地震COSI-Corr方法与光流场方法结果定量对比

Table 3 Quantitative Comparison of Results from the COSI-Corr Method and Optical Flow Field Method for the California Earthquake

方向	残差平均值/m	残差标准差/m	光流场方法稳定区域标准差/m	COSI-Corr方法稳定区域标准差/m	皮尔逊相关系数	拟合RMSE/m	光流场方法解算时间/min	COSI-Corr方法解算时间/min
东西向	0.012	0.449	0.25	0.36	0.785	0.27	5	96
南北向	0.017	0.443	0.29	0.37	0.882	0.28	5	96

下载: 导出CSV

表 4 白格滑坡COSI-Corr方法与光流场方法结果定量对比

Table 4 Quantitative Comparison of the Results of COSI-Corr Method and Optical Flow Field Method for the Baige Landslide

影像类型	方法	稳定区域标准差/m	最大位移/m	平均位移/m	解算时间/s	覆盖范围/%
光学影像	光流场方法	0.36	34.15	27.75	7	98.2
光学影像	COSI-Corr（64×64）	0.28	34.76	28.13	177	72.3

下载: 导出CSV

参考文献(40)

[1]	Lacroix P, Handwerger A L, Bièvre G. Life and Death of Slow-Moving Landslides[J]. Nature Reviews Earth & Environment, 2020, 1（8）： 404-419.
[2]	He Y, Zhao Z, Yang W, et al. A Unified Network of Information Considering Superimposed Landslide Factors Sequence and Pixel Spatial Neighbourhood for Landslide Susceptibility Mapping[J]. International Journal of Applied Earth Observation and Geoinformation, 2021, 104： 102508.
[3]	Song C, Yu C, Li Z, et al.Triggering and Recovery of Earthquake Accelerated Landslides in Central Italy Revealed by Satellite Radar Observations[J]. Nature Communications, 2022, 13（1）： 7278.
[4]	李振洪, 韩炳权, 刘振江, 等. InSAR数据约束下2016年和2022年青海门源地震震源参数及其滑动分布[J]. 武汉大学学报（信息科学版）, 2022, 47（6）： 887-897. Li Zhenhong, Han Bingquan, Liu Zhenjiang, et al. Source Parameters and Slip Distributions of the 2016 and 2022 Menyuan Qinghai Earthquakes Constrained by InSAR Observations [J]. Geomatics and Information Science of Wuhan University, 2022, 47（6）： 887-897.
[5]	He Y, Zhao Z, Zhu Q, et al. An Integrated Neural Network Method for Landslide Susceptibility Assessment Based on Time-Series InSAR Deformation Dynamic Features[J]. International Journal of Digital Earth, 2024, 17（1）： 2295408.
[6]	李振洪, 宋闯, 余琛, 等. 卫星雷达遥感在滑坡灾害探测和监测中的应用：挑战与对策[J]. 武汉大学学报（信息科学版）, 2019, 44（7）： 967-979. Li Zhenhong, Song Chuang, Yu Chen, et al. Application of Satellite Radar Remote Sensing to Landslide Detection and Monitoring： Challenges and Solutions[J]. Geomatics and Information Science of Wuhan University, 2019, 44（7）： 967-979.
[7]	王乐洋, 邹阿健. 结合SAR和光学数据检索凯库拉Mw 7.8地震三维形变[J]. 武汉大学学报（信息科学版）, 2024, 49（2）： 303-312. Wang Leyang, Zou Ajian. Retrieving 3D Coseismic Deformation of 2016 Mw 7.8 Kaikoura Earthquake Using SAR and Optical Data[J]. Geomatics and Information Science of Wuhan University, 2024, 49（2）： 303-312.
[8]	Provost F,Michéa D,Malet J P,et al.Terrain Deformation Measurements from Optical Satellite Imagery： The MPIC-OPT Processing Services for Geohazards Monitoring[J]. Remote Sensing of Environment, 2022, 274： 112949.
[9]	李振洪, 朱武, 余琛, 等. 影像大地测量学发展现状与趋势[J]. 测绘学报, 2023, 52（11）： 1805-1834. Li Zhenhong, Zhu Wu, Yu Chen, et al. Development Status and Trends of Imaging Geodesy[J]. Acta Geodaetica et Cartographica Sinica, 2023, 52（11）： 1805-1834.
[10]	Leprince S, Ayoub F, Klinger Y, et al. Co-Registration of Optically Sensed Images and Correlation （COSI-Corr）： An Operational Methodology for Ground Deformation Measurements[C]//IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 2007.
[11]	Rosu A M, Pierrot-Deseilligny M, Delorme A, et al. Measurement of Ground Dsplacement from Optical Satellite Image Correlation Using the Free Open-Source Software MicMac[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 100： 48-59.
[12]	Cournet M, Giros A, Dumas L, et al. 2D Sub-Pixel Disparity Measurement Using QPEC/Medicis[J]. ISPRS International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016, XLI（B1）： 291-298.
[13]	Lacroix P, Araujo G, Hollingsworth J, et al. Self-entrainment Motion of a Slow-Moving Landslide Inferred From Landsat-8 Time Series[J]. Journal of Geophysical Research： Earth Surface, 2019, 124（5）： 1201-1216.
[14]	熊俊麟, 范宣梅, 窦向阳, 等. 藏东南然乌湖流域雅弄冰川流速季节性变化[J]. 武汉大学学报（信息科学版）, 2021, 46（10）： 1579-1588. Xiong Junlin, Fan Xuanmei, Dou Xiangyang, et al. Seasonal Variation of Yalong Glacier’s Velocity in Ranwu Lake Basin, Southeast Tibetan Plateau[J]. Geomatics and Information Science of Wuhan University, 2021, 46（10）： 1579-1588.
[15]	Ding C, Zhang L, Liao M, et al. Quantifying the Spatiotemporal Patterns of Dune Migration Near Minqin Oasis in Northwestern China with Time Series of Landsat-8 and Sentinel-2 Observations[J]. Remote Sensing of Environment,2020,236： 111498.
[16]	贺礼家, 冯光财, 冯志雄, 等. 哨兵-2号光学影像地表形变监测：以2016年Mw 7.8新西兰凯库拉地震为例[J]. 测绘学报, 2019, 48（3）： 339-351. He Lijia, Feng Guangcai, Feng Zhixiong, et al. Coseismic Displacements of 2016 Mw 7.8 Kaikoura, New Zealand Earthquake, Using Sentinel-2 Optical Images[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48（3）： 339-351.
[17]	Cai J, Wang C, Mao X, et al. An Adaptive Offset Tracking Method with SAR Images for Landslide Displacement Monitoring[J]. Remote Sensing, 2017, 9（8）： 830.
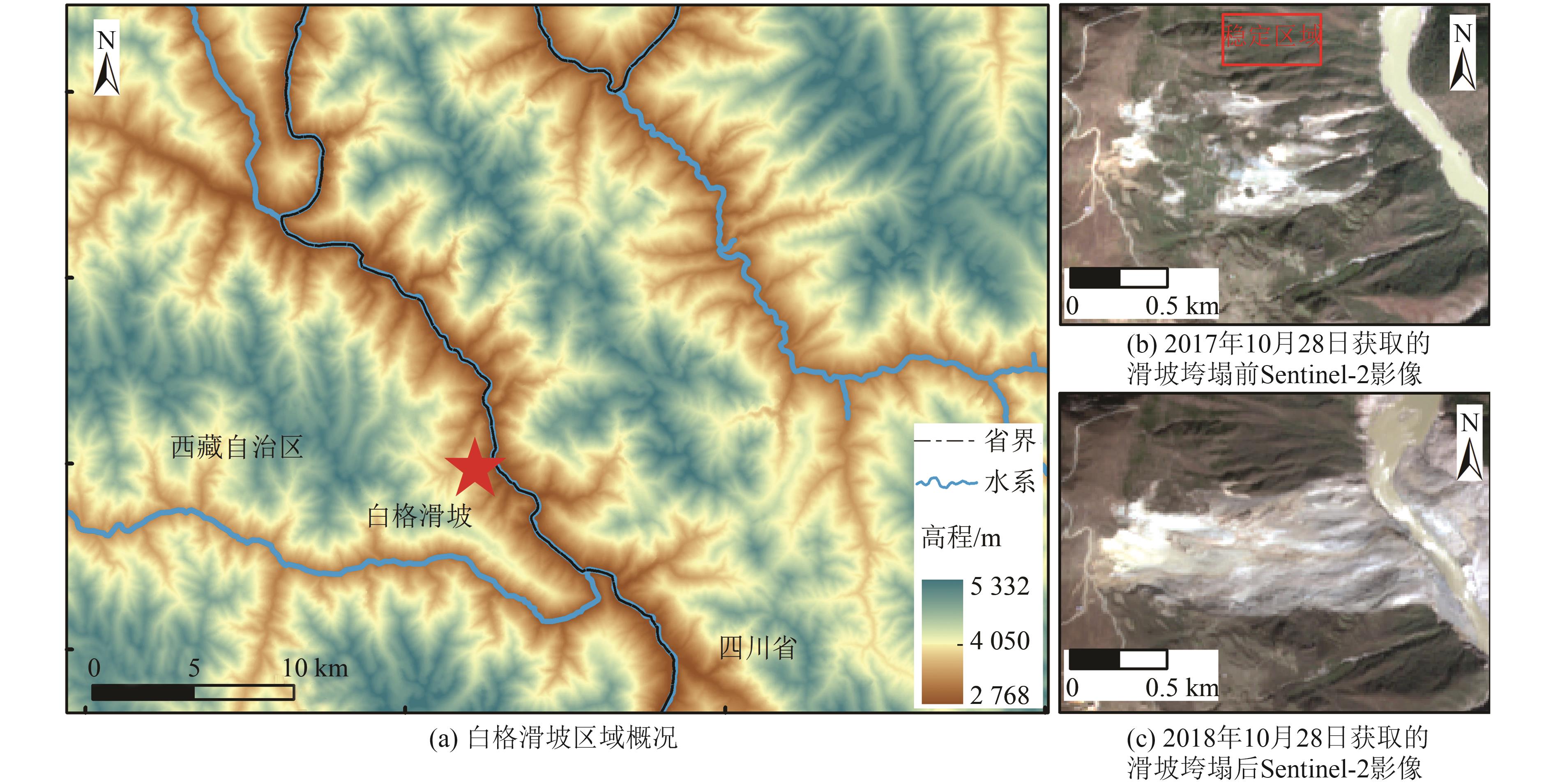
[18]	Li M, Zhang L, Dong J, et al. Characterization of Pre- and Post-Failure Displacements of the Huangnibazi Landslide in Li County with Multi-source Satellite Observations[J]. Engineering Geology, 2019, 257： 105140.
[19]	Jia H, Wang Y, Ge D, et al. Improved Offset Tracking for Predisaster Deformation Monitoring of the 2018 Jinsha River Landslide （Tibet, China）[J]. Remote Sensing of Environment,2020,247： 111899.
[20]	Horn B K P, Schunck B G. Determining Optical Flow[J]. Artificial Intelligence,1981,17： 185-203.
[21]	Brigot G,Colin-Koeniguer E,Plyer A,et al. Adaptation and Evaluation of an Optical Flow Method Applied to Coregistration of Forest Remote Sensing Images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9（7）： 2923-2939.
[22]	Fu Y, Zhang B, Liu G, et al. An Optical Flow SBAS Technique for Glacier Surface Velocity Extraction Using SAR Images[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19： 1-5.
[23]	Chanut M A, Gasc-Barbier M, Dubois L, et al. Automatic Identification of Continuous or Non-continuous Evolution of Landslides and Quantification of Deformations[J]. Landslides, 2021, 18（9）： 3101-3118.
[24]	Hermle D, Gaeta M, Krautblatter M, et al. Performance Testing of Optical Flow Time Series Analyses Based on a Fast, High-Alpine Landslide[J]. Remote Sensing, 2022, 14（3）： 455.
[25]	Drusch M, Del Bello U, Carlier S, et al. Sentinel-2： ESA’s Optical High-Resolution Mission for GMES Operational Services[J]. Remote Sensing of Environment, 2012, 120： 25-36.
[26]	Xu Y, Lu Z, Schulz W H, et al. Twelve-Year Dynamics and Rainfall Thresholds for Alternating Creep and Rapid Movement of the Hooskanaden Landslide from Integrating InSAR, Pixel Offset Tracking, and Borehole and Hydrological Measurements[J]. Journal of Geophysical Research： Earth Surface, 2020, 125（10）, DOI：10.1029/2020JF005640. doi: 10.1029/2020JF005640
[27]	Tang C H, Lin Y N, Tung H, et al. Nearby Fault Interaction Within the Double-Vergence Suture in Eastern Taiwan During the 2022 Chihshang Earthquake Sequence[J]. Communications Earth & Environment, 2023, 4（1）： 333.
[28]	Kirst C, Skriabine S, Vieites-Prado A, et al. Mapping the Fine-Scale Organization and Plasticity of the Brain Vasculature[J]. Cell, 2020, 180（4）： 780-795.
[29]	Ali E, Xu W, Ding X. Improved Optical Image Matching Time Series Inversion Approach for Monitoring Dune Migration in North Sinai Sand Sea： Algorithm Procedure, Application, and Validation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, 164： 106-124.
[30]	Bontemps N,Lacroix P, Doin M P. Inversion of Deformation Fields Time-Series from Optical Images, and Application to the Long Term Kinematics of Slow-Moving Landslides in Peru[J]. Remote Sensing of Environment, 2018, 210： 144-158.
[31]	Yang W, Liu L, Shi P. Detecting Precursors of an Imminent Landslide Along the Jinsha River[J].Natural Hazards and Earth System Sciences, 2020, 20（11）： 3215-3224.
[32]	Okada Y. Internal Deformation Due to Shear and Tensile Faults in a Half-Space[J]. Bulletin of the Seismological Society of America, 1992, 82（2）： 1018-1040.
[33]	Zhang Y, Zheng X, Chen Q, et al. Automatic Inversion of Rupture Processes of the Foreshock and Mainshock and Correlation of the Seismicity During the 2019 Ridgecrest Earthquake Sequence[J]. Seismological Research Letters, 2020, 91（3）： 1556-1566.
[34]	Chen K, Avouac J P, Aati S, et al. Cascading and Pulse-Like Ruptures During the 2019 Ridgecrest Earthquakes in the Eastern California Shear Zone[J]. Nature Communications, 2020, 11（1）： 22.
[35]	马振宁, 钱荣毅, Catchings R, 等. 美国南加州Ridgecrest Mw 6.4~Mw 7.1地震地表破裂几何学及运动学特征[J]. 地球物理学报, 2021, 64（4）： 1206-1214. Ma Zhenning, Qian Rongyi, Catchings R, et al. Geometric and Kinematic Characteristics of Surface Ruptures of Ridgecrest Mw 6.4—Mw 7.1 Earthquake in Southern California[J]. Chinese Journal of Geophysics, 2021, 64（4）： 1206-1214.
[36]	Fan X, Xu Q, Alonso-Rodriguez A, et al. Successive Landsliding and Damming of the Jinsha River in Eastern Tibet, China： Prime Investigation, Early Warning, and Emergency Response[J]. Landslides, 2019, 16（5）： 1003-1020.
[37]	许强, 郑光, 李为乐, 等. 2018年10月和11月金沙江白格两次滑坡-堰塞堵江事件分析研究[J].工程地质学报,2018,26（6）： 1534-1551. Xu Qiang,Zhang Guang,Li Weile,et al.Study on Successive Landslide Damming Events of Jinsha River in Baige Village on Octorber 11 and November 3,2018[J]. Journal of Engineering Geology,2018,26（6）： 1534-1551.
[38]	Li M, Zhang L, Ding C, et al. Retrieval of Historical Surface Displacements of the Baige Landslide from Time-Series SAR Observations for Retrospective Analysis of the Collapse Event[J]. Remote Sensing of Environment, 2020, 240： 111695.
[39]	柳林, 宋豪峰, 杜亚男, 等. 联合哨兵2号和Landsat 8估计白格滑坡时序偏移量[J]. 武汉大学学报（信息科学版）, 2021, 46（10）： 1461-1470. Liu Lin, Song Haofeng, Du Yanan, et al. Time⁃Series Offset Tracking of the Baige Landslide Based on Sentinel⁃2 and Landsat-8[J]. Geomatics and Information Science of Wuhan University,2021,46（10）：1461-1470.
[40]	Yang W. Selecting the Best Image Pairs to Measure Slope Deformation[J].Sensors,2020,20（17）： 4721.