Population Analysis Unit Expression Considering Urban Scene Changes
-
摘要:
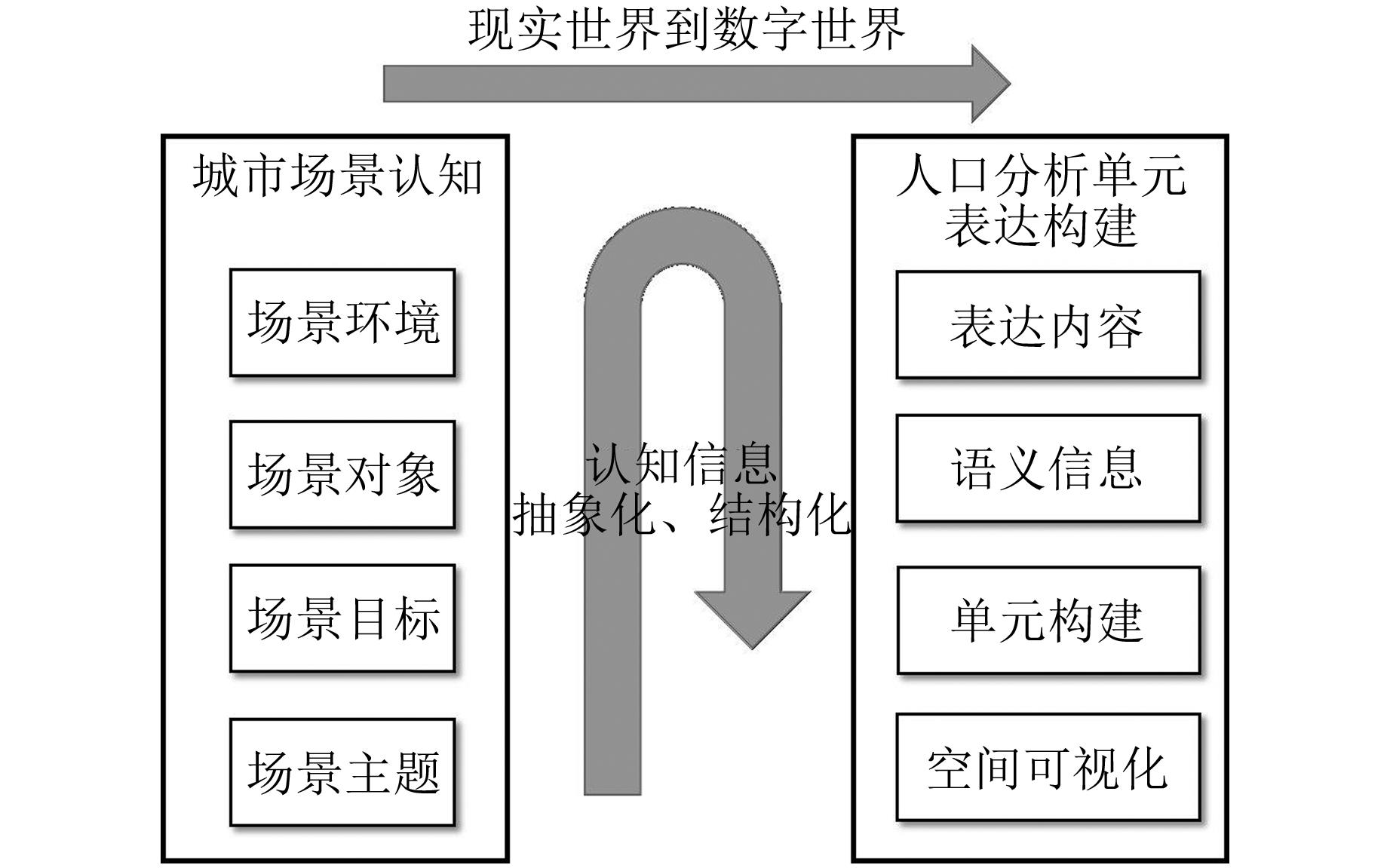
人口分析单元是不同城市场景开展地理分析的时空对象和基本单位。城市场景是人口时空活动的信息描述集合,为单元表达提供时空范围与语义限定。针对当前单元表达模型较少关注具体人口分析特征描述,缺乏场景和单元特征表达的关联方法和参考标准的问题,提出了顾及城市场景变化的人口分析单元表达模型。该模型首先考虑场景要素与人口活动特征在单元中的表达关联,形成融合场景组成要素的人口分析单元表达方法。然后,根据具体表达内容分析场景和单元的关联特征及统一参考标准,构建关联场景的单元形式化描述结构。具体案例表明所提出的模型可将城市场景信息按标准关联人口分析单元特征,提高了单元的特征表达能力和对场景的适用性,并为单元几何构建提供了参考。
Abstract:ObjectivesPopulation analysis unit is the spatiotemporal object and basic part of geographical analysis in different urban scenes. Aiming at the problem that the current unit expression model pays less attention to the description of specific population analysis features and lacks the correlation method and referen‑ce standard of scene and unit feature expression. We propose a population analysis unit expression model considering urban scene change.
MethodsThe model first considers the unit's demand for feature description of population spatiotemporal analysis in two-dimensional space, as well as the dissimilarity of components such as objects and environments of urban scenes, forming a population analysis unit expression model that integrates scene components. Then, based on the content of model expression, the relationship between urban scene and population analysis unit is analyzed. Referring to the geographic scene modeling method, the correlation characteristics and reference standards between scene and population analysis unit are constructed.
ResultsIn order to verify the rationality of the method, we take the epidemic analysis scenario in Wuhan City, Hubei Province, China as a case to realize the population analysis unit modeling and attribute feature dynamic update considering the scenario change. The results show that the proposed model can correlate urban scene information with population analysis unit characteristics according to standards and help to improve unit description ability.
ConclusionsBy associating the information and characteristics of urban scene elements, the proposed model can enhance the expression ability of units and map the information and characteristics of urban scene in a more standard and reasonable way. It can also provide a referen‑
ce for the geometric construction of the unit and the interpretation of the analysis results.
-
经典平差模型和最小二乘估计理论[1]在大地测量等众多科学研究和工程领域中应用广泛，其中，高斯-马尔科夫模型（Gauss-Markov model, GMM）最为常用，而高斯-赫尔默特模型（GaussHelmert model, GHM）可视为经典平差模型的一般通用形式。在实际应用中，坐标转换、回归模型、数字地面模型和大地测量反演等平差模型的系数矩阵包含随机的观测误差，从而使得GMM扩展为随机系数矩阵的变量含误差（errors-invariables, EIV）模型[2]。文献[3]提出同时顾及观测向量和系数矩阵中随机误差的整体最小二乘（total least squares, TLS）估计算法。TLS的非线性特征导致其受制于计算机技术的发展，直至20世纪80年代，文献[4]将TLS引入数值分析领域并提出奇异值分解算法，TLS才开始广泛应用于各专业领域并取得丰富的研究成果。文献[2]中对TLS进行了改进和扩展；文献[5]从TLS的算法、统计特性和可靠性研究等方面综述了TLS方法的研究进展。当误差相关且精度不等时，采用加权整体最小二乘估计（weighted total least squares, WTLS）方法进行求解。文献[6]研究了基于高斯-牛顿迭代法的WTLS算法，该算法假设权矩阵为特殊情况，得到的解在形式上与最小二乘（least squares, LS）解相同；文献[7]研究了在任意权矩阵的一般情况下的WTLS算法；文献[8]研究了特殊结构下WTLS算法的迭代方法并将其应用于实际场景；文献[9-12]研究了附有等式和不等式约束情况下的WTLS算法；文献[13]研究了稳健WTLS算法。
通过对EIV模型的形式进行变换，文献[14]提出部分EIV(partial EIV, PEIV）模型，提高了系数矩阵仅含部分随机量情况下的计算效率。文献[15]对PEIV模型进行线性化，推导了PEIV模型的LS算法。文献[16-17]从模型的一般性出发，将EIV模型扩展至通用EIV模型，将经典平差的GHM中观测向量的系数矩阵和参数向量的系数矩阵由固定矩阵推广为随机矩阵，涵括随机系数矩阵的各类情况，同时推导了通用EIV模型在任意权矩阵情况下的一般性WTLS算法。
通用EIV模型的非线性使得该算法在估计量较多时计算量大。本文利用非线性平差原理，将通用EIV模型展开后的二阶项纳入平差方程的常数项，从而将其转化为GHM形式，推导出通用EIV模型的线性化整体最小二乘（linearized total least squares, LTLS）算法。相较于WTLS算法，LTLS算法提高了通用EIV模型的计算效率，当参数向量初始值与最优值相差较大时，提升了迭代收敛速度。
1 通用EIV平差模型及其WTLS估计
1.1 通用EIV平差模型
GHM的形式为：
$$ \mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{y}} + {\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{y}}}} \right) + \mathit{\boldsymbol{BX}} + \mathit{\boldsymbol{w}} = \mathit{\boldsymbol{0}} $$ (1) 式中，y和vy分别为n×1维观测值向量和观测值改正数向量；X为u×1维参数向量；A为观测值向量对应的f×n维系数矩阵；B为参数向量对应的f×u维系数矩阵；w为f×1维常数向量；在经典平差函数模型的定义中，A和B均不含随机误差，为固定矩阵。
当参数向量的系数矩阵B含随机误差时，GHM（式（1））扩展为经典EIV模型。当观测值向量的系数矩阵A和参数向量的系数矩阵B均含随机误差时，GHM（式（1））扩展为通用EIV平差模型[16]:
$$ \left( {\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{A}}}} \right)\left( {\mathit{\boldsymbol{y}} + {\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{y}}}} \right) + \left( {\mathit{\boldsymbol{B}} + {\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{B}}}} \right)\mathit{\boldsymbol{X}} + \mathit{\boldsymbol{w}} = \mathit{\boldsymbol{0}} $$ (2) 式中，A和VA分别为观测值向量对应的f×n维系数矩阵及其改正数矩阵；B和VB分别为参数向量对应的f×u维系数矩阵及其改正数矩阵。由于A、B和y均为随机矩阵，则通用EIV的随机模型为：
$$ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {{\mathop{\rm vec}\nolimits} (\mathit{\boldsymbol{A}})}\\ {{\mathop{\rm vec}\nolimits} (\mathit{\boldsymbol{B}})}\\ \mathit{\boldsymbol{y}} \end{array}} \right],\mathit{\boldsymbol{v}} = \left[ {\begin{array}{*{20}{c}} {{\mathop{\rm vec}\nolimits} \left( {{\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{A}}}} \right)}\\ {{\mathop{\rm vec}\nolimits} \left( {{\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{B}}}} \right)}\\ {{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{y}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{A}}}}\\ {{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{B}}}}\\ {{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{y}}}} \end{array}} \right] $$ (3) $$ \mathit{\boldsymbol{D}}(\mathit{\boldsymbol{L}}) = \delta _0^2{\mathit{\boldsymbol{P}}^{ - 1}} = \delta _0^2\mathit{\boldsymbol{Q}} = \delta _0^2\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{A}}}}&{{\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{AB}}}}}&{{\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{Ay}}}}}\\ {{\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{BA}}}}}&{{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{B}}}}&{{\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{By}}}}}\\ {{\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{yA}}}}}&{{\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{yB}}}}}&{{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{y}}}} \end{array}} \right] $$ (4) 式中，vec(.)表示将矩阵按列向量化；L和v分别为观测数据的k×1维观测值向量及其改正数向量，包括A、B和y中所有观测值及其改正数，其中k=fn+fu+n; P、Q和D(L)分别为L的权矩阵、协因数矩阵和方差协方差矩阵；δ02为单位权方差。
1.2 WTLS估计
根据TLS准则，通用EIV平差模型的求解可转化为最优化估计问题[16]:
$$ \left\{ {\begin{array}{*{20}{l}} {\min {\mathit{\boldsymbol{v}}^{\rm{T}}}\mathit{\boldsymbol{Pv}}}\\ {s.t.{\rm{ }}\left( {\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{A}}}} \right)\left( {\mathit{\boldsymbol{y}} + {\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{y}}}} \right) + \left( {\mathit{\boldsymbol{B}} + {\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{B}}}} \right)\mathit{\boldsymbol{X}} + \mathit{\boldsymbol{w}} = \mathit{\boldsymbol{0}}} \end{array}} \right. $$ (5) 相应目标函数为：
$$ \begin{array}{*{20}{c}} {\mathit{\Phi }(\mathit{\boldsymbol{r}},\mathit{\boldsymbol{\lambda }},\mathit{\boldsymbol{X}}) = {\mathit{\boldsymbol{v}}^{\rm{T}}}\mathit{\boldsymbol{Pv}} + 2{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\left( {\mathit{\boldsymbol{Ay}} + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{y}}} + } \right.}\\ {\left. {{\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{A}}}\mathit{\boldsymbol{y}} + {\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{A}}}{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{y}}} + \mathit{\boldsymbol{BX}} + {\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{B}}}\mathit{\boldsymbol{X}} + \mathit{\boldsymbol{w}}} \right)} \end{array} $$ (6) 将目标函数对估计量分别求偏导并令其等于0，得到非线性方程组：
$$ \frac{{\partial \mathit{\Phi }}}{{\partial \mathit{\boldsymbol{\hat X}}}} = 2\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{\hat \lambda }} + \mathit{\boldsymbol{\hat V}}_\mathit{\boldsymbol{B}}^{\rm{T}}\mathit{\boldsymbol{\hat \lambda }}} \right) = \mathit{\boldsymbol{0}} $$ (7) $$ \frac{{\partial \mathit{\Phi }}}{{\partial \mathit{\boldsymbol{\hat v}}}} = 2\left( {\mathit{\boldsymbol{P\hat v}} + {{\mathit{\boldsymbol{\hat C}}}^{\rm{T}}}\mathit{\boldsymbol{\hat \lambda }}} \right) = \mathit{\boldsymbol{0}} $$ (8) $$ \frac{{\partial \mathit{\Phi }}}{{\partial \mathit{\boldsymbol{\hat \lambda }}}} = 2(\mathit{\boldsymbol{Ay}} + \mathit{\boldsymbol{B\hat X}} + \mathit{\boldsymbol{\hat C\hat v}} + \mathit{\boldsymbol{w}}) = \mathit{\boldsymbol{0}} $$ (9) 式中，$ {\boldsymbol{C}}=\left[{\boldsymbol{y}}^{\mathrm{T}} \otimes {\boldsymbol{I}}_{f} \boldsymbol{X}^{\mathrm{T}} \otimes {\boldsymbol{I}}_{f} A+\boldsymbol{V}_{{\boldsymbol{A}}}\right] ; \hat{{\boldsymbol{v}}}, \hat{\boldsymbol{X}} $分别为观测值向量和参数向量的估计值。
根据式（7）~式（9）可导出：
$$ \mathit{\boldsymbol{\hat v}} = - \mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{\hat C}}^{\rm{T}}}\mathit{\boldsymbol{\hat Q}}_\mathit{\boldsymbol{C}}^{ - 1}(\mathit{\boldsymbol{Ay}} + \mathit{\boldsymbol{B\hat X}} + \mathit{\boldsymbol{w}}) $$ (10) $$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}} = - {{\left[ {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}} + \mathit{\boldsymbol{\hat V}}_\mathit{\boldsymbol{B}}^{\rm{T}}} \right)\mathit{\boldsymbol{\hat Q}}_\mathit{\boldsymbol{C}}^{ - 1}\mathit{\boldsymbol{B}}} \right]}^{ - 1}}\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}} + } \right.}\\ {\left. {\mathit{\boldsymbol{\hat V}}_\mathit{\boldsymbol{B}}^{\rm{T}}} \right)\mathit{\boldsymbol{\hat Q}}_\mathit{\boldsymbol{C}}^{ - 1}(\mathit{\boldsymbol{Ay}} + \mathit{\boldsymbol{w}})} \end{array} $$ (11) 式中，$ \hat{\boldsymbol{Q}}_{C}=\hat{\boldsymbol{C}} \boldsymbol{Q} \hat{\boldsymbol{C}}^{\mathrm{T}} $。
以式（2）的LS解作为初始值，根据式（10）和式（11）进行迭代计算可得通用EIV模型的WTLS最优解。
2 通用EIV模型的线性化估计算法
通用EIV模型是非线性模型，观测值矩阵和系数矩阵均为随机量，WTLS算法的计算量随着待估量个数增多将迅速增加。将式（2）展开，利用非线性函数平差原理[18]将二阶项作为模型误差纳入方程的常数项，从而将通用EIV模型转化为线性的GHM，推导出通用EIV模型的LTLS算法。
令X=X0+x，将式（2）展开得：
$$ \begin{array}{c} \left( {{\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{A}}}\mathit{\boldsymbol{y}} + {\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{B}}}{\mathit{\boldsymbol{X}}_0} + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{y}}}} \right) + \mathit{\boldsymbol{Bx}} + (\mathit{\boldsymbol{w}} + \mathit{\boldsymbol{Ay}} + \\ \left. {\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{X}}_0} + {\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{A}}}{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{y}}} + {\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{B}}}\mathit{\boldsymbol{x}}} \right) = \mathit{\boldsymbol{0}} \end{array} $$ (12) 式（12）可表示为：
$$ \begin{array}{*{20}{c}} {\left[ {\left( {{\mathit{\boldsymbol{y}}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_\mathit{\boldsymbol{f}}}} \right){\mathop{\rm vec}\nolimits} \left( {{\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{A}}}} \right) + \left( {\mathit{\boldsymbol{X}}_0^{\rm{T}} \otimes {\mathit{\boldsymbol{I}}_\mathit{\boldsymbol{f}}}} \right){\mathop{\rm vec}\nolimits} \left( {{\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{B}}}} \right) + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{y}}}} \right] + }\\ {\mathit{\boldsymbol{Bx}} + \left( {\mathit{\boldsymbol{w}} + \mathit{\boldsymbol{Ay}} + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{X}}_0} + {\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{A}}}{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{y}}} + {\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{B}}}\mathit{\boldsymbol{x}}} \right) = \mathit{\boldsymbol{0}}} \end{array} $$ (13) 则通用EIV模型的线性化形式为：
$$ {\mathit{\boldsymbol{A}}_\mathit{\boldsymbol{l}}}{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{l}}} + \mathit{\boldsymbol{Bx}} + {\mathit{\boldsymbol{w}}_\mathit{\boldsymbol{l}}} = \mathit{\boldsymbol{0}} $$ (14) 式中，$ {\boldsymbol{A}}_{{\boldsymbol{l}}}=\left[\begin{array}{llll} {\boldsymbol{y}}^{\mathrm{T}} \otimes {\boldsymbol{I_{f}}} & \boldsymbol{X}_{0}^{\mathrm{T}} & \otimes {\boldsymbol{I_{f}}} & {\boldsymbol{A}} \end{array}\right] ; \ {\boldsymbol{v_{l}}}= \left[\begin{array}{c} \operatorname{vec}\left(\boldsymbol{V}_{{\boldsymbol{A}}}\right) \\ \operatorname{vec}\left(\boldsymbol{V}_{{\boldsymbol{B}}}\right) \\ \boldsymbol{v}_{{\boldsymbol{y}}} \end{array}\right] ; \boldsymbol{w}_{{\boldsymbol{l}}}=\boldsymbol{w}+\boldsymbol{Ay} + {\boldsymbol{B}} \boldsymbol{X}_{0}+\boldsymbol{V}_{{\boldsymbol{A}}} \boldsymbol{v}_{{\boldsymbol{y}}}+\boldsymbol{V}_{{\boldsymbol{B}}} {\boldsymbol{x}}$为常数项，即将式（2）按泰勒展开略去的二阶项VAvy+VBx作为模型误差纳入常数项。
由式（14）可知，线性化后的通用EIV模型与GHM形式一致，可使用最小二乘法得到观测值向量和参数向量：
$$ \mathit{\boldsymbol{\hat x}} = - \mathit{\boldsymbol{\hat N}}_{\mathit{\boldsymbol{bb}}}^{ - 1}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{\hat N}}_{\mathit{\boldsymbol{aa}}}^{ - 1}{\mathit{\boldsymbol{w}}_\mathit{\boldsymbol{l}}} $$ (15) $$ {{\mathit{\boldsymbol{\hat v}}}_\mathit{\boldsymbol{l}}} = - \mathit{\boldsymbol{Q}}{{\mathit{\boldsymbol{\hat A}}}_\mathit{\boldsymbol{l}}}\mathit{\boldsymbol{\hat N}}_{\mathit{\boldsymbol{aa}}}^{ - 1}\left( {\mathit{\boldsymbol{B\hat x}} + {\mathit{\boldsymbol{w}}_\mathit{\boldsymbol{l}}}} \right) $$ (16) 式中，$ \boldsymbol{N}_{{\boldsymbol{a a}}}=\boldsymbol{A}_{{\boldsymbol{l}}} \boldsymbol{Q} \boldsymbol{A}_{{\boldsymbol{l}}}^{\mathrm{T}} ; \boldsymbol{N}_{{\boldsymbol{b b}}}= {\boldsymbol{B}}^{\mathrm{T}} \boldsymbol{N}_{{\boldsymbol{a a}}}^{-1} {\boldsymbol{B}} $; Q为观测值向量的协因数矩阵。
通用EIV模型的LTLS算法步骤如下：
1）将实际模型表示为式（2），将观测数据代入得到A、B和y矩阵，并给出观测值数据的协因数阵Q，包括观测值向量Qy、观测值向量系数矩阵QA、参数向量系数矩阵QB。
2）计算通用EIV模型的LS解作为初始参数解：$ \hat{\boldsymbol{X}}^{0}=-\left({\boldsymbol{B}}^{\mathrm{T}}\left({\boldsymbol{A }}\boldsymbol{Q}_{{\boldsymbol{y}}} {\boldsymbol{A}}^{\mathrm{T}}\right)^{-1} {\boldsymbol{B}}\right)^{-1} {\boldsymbol{B}}^{\mathrm{T}}\left({\boldsymbol{A}} \boldsymbol{Q}_{{\boldsymbol{y}}} {\boldsymbol{A}}^{\mathrm{T}}\right)^{-1} · ({\boldsymbol{A y}}+{\boldsymbol{w}})$, 观测值向量改正数初始值取0。
3）根据式（15）和式（16）进行迭代计算，每次迭代将上一次估计值作为初始值代入新的迭代过程，直至前后两次估计值之差小于设定阈值。
GHM按泰勒级数展开仅包含常数项、一阶项（二阶及以上项全部为零），将二阶项纳入线性化后的常数项，该方法极大地减弱了线性化引起的模型误差。因此，在同样以LS解作为初值的情况下，GHM线性化的LTLS解与WTLS解的收敛性一致。此外，根据文献[19]中EIV模型LS解偏差的研究结果，在当前测量技术手段和观测精度条件下，以有偏的LS解作为初值，能够保证TLS迭代计算收敛，除非出现极特殊情况导致LS初始解严重偏离最优值。
参考GHM，式（2）的LTLS算法估计结果的精度计算式为：
$$ \left\{ {\begin{array}{*{20}{l}} {\hat \delta _0^2 = \mathit{\boldsymbol{v}}_\mathit{\boldsymbol{l}}^{\rm{T}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{l}}}/\mathit{r}}\\ {\mathit{\boldsymbol{Q}}(\mathit{\boldsymbol{\hat x}}) = {{\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{A}}_\mathit{\boldsymbol{l}}}\mathit{\boldsymbol{QA}}_\mathit{\boldsymbol{l}}^{\rm{T}}} \right)}^{ - 1}}\mathit{\boldsymbol{B}}} \right)}^{ - 1}}}\\ {\mathit{\boldsymbol{Q}}(\mathit{\boldsymbol{\hat L}}) = \mathit{\boldsymbol{Q}} - \mathit{\boldsymbol{QA}}_\mathit{\boldsymbol{l}}^{\rm{T}}\left( {\mathit{\boldsymbol{N}}_\mathit{\boldsymbol{A}}^{ - 1}\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{\hat x}}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{N}}_\mathit{\boldsymbol{A}}^{ - 1}} \right){\mathit{\boldsymbol{A}}_\mathit{\boldsymbol{l}}}\mathit{\boldsymbol{Q}}} \right)}\\ {\mathit{\boldsymbol{D}}(\mathit{\boldsymbol{\hat x}}) = \hat \delta _0^2\mathit{\boldsymbol{Q}}(\mathit{\boldsymbol{\hat x}})}\\ {\mathit{\boldsymbol{D}}(\mathit{\boldsymbol{\hat L}}) = \hat \delta _0^2\mathit{\boldsymbol{Q}}(\mathit{\boldsymbol{\hat L}})} \end{array}} \right. $$ (17) 式中，多余观测数r=n-t; n为观测值个数；t为必要观测值个数；r与GHM的多余观测数相同；$ \boldsymbol{N}_{{\boldsymbol{A}}}=\boldsymbol{A}_{{\boldsymbol{l}}} \boldsymbol{P}^{-1} \boldsymbol{A}_{{\boldsymbol{l}}}^{\mathrm{T}} $。
3 LTLS算法实例分析
按照LTLS算法步骤设计实验，比较LTLS算法与WTLS算法的计算结果，验证LTLS算法的正确性、高效性和可行性。实验1设计模拟数据，比较分析单组实验结果和1 000组实验统计结果，验证LTLS算法的正确性；实验2在待估计量数目取不同量级时，比较两种算法的计算时间，验证LTLS算法的高效性；实验3通过实例验证LTLS算法的可行性。
3.1 实验1
在通用EIV模型（式（2））中，设置参数真值X=[5 10]T，系数矩阵A和B中随机量的中误差分别设为0.01和0.02，观测向量y的中误差设为0.03。A、B、y和常数向量w的模拟数据如下：
$$ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {12.469}&{11.096}&{15.872}&{11.725}\\ {8.883}&{10.291}&{2.929}&{3.666}\\ {12.321}&{1.109}&{6.392}&{15.809}\\ {3.551}&{12.104}&{3.867}&{1.257} \end{array}} \right], $$ $$ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{l}} {10.410}&{17.544}\\ {18.033}&{15.171}\\ {18.631}&{15.855}\\ {15.671}&{11.878} \end{array}} \right], $$ $$ \mathit{\boldsymbol{y}} = \left[ {\begin{array}{*{20}{l}} {27.543}\\ {20.727}\\ {20.839}\\ {25.033} \end{array}} \right],\mathit{\boldsymbol{w}} = \left[ {\begin{array}{*{20}{c}} { - 1425.323}\\ { - 852.619}\\ { - 1142.913}\\ { - 658.407} \end{array}} \right]。 $$ 采用LTLS算法和WTLS算法的估计结果如表 1所示，LTLS参数解与WTLS参数解完全相等，验证了LTLS算法的正确性。
表 1 参数解及其方差估计值Table 1. Parameter Values and Mean Square Deviations算法 参数解 中误差 $ \hat {\boldsymbol{X}} _1 $ $ \hat {\boldsymbol{X}} _2 $ $ σ _{\hat{\boldsymbol{X}}_1} $ $ σ_ {\hat{\boldsymbol{X}}_2} $ LTLS算法 5.012 551 9.994 964 0.039 9 0.051 9 WTLS算法 5.012 551 9.994 964 0.039 9 0.051 9 为了进一步验证LTLS算法的正确性，首先采用模拟的1 000组数据计算LTLS和WTLS参数解的均值$ {\rm{avg}} (\hat {\boldsymbol{X}} _1) 和 {\rm{avg}} (\hat {\boldsymbol{X}} _2) $，并将参数解均值代入式（17），求得LTLS参数解的协因数阵估值$ {\boldsymbol{Q}}(\hat {\boldsymbol{X}} )$，然后利用参数真值求得精确的参数协因数阵$ \overline{\boldsymbol{Q}}(\hat{\boldsymbol{X}})={\boldsymbol{E}}_{{\boldsymbol{X}}}^{\mathrm{T}} \boldsymbol{E}_{{\boldsymbol{X}}} /(m-n) , {\boldsymbol{E}}_{{\boldsymbol{X}}}=\left[\begin{array}{ll} \hat{{\boldsymbol{X}}}_{1}^{(j)}-5 & \hat{{\boldsymbol{X}}}_{2}^{(j)}-10 \end{array}\right] $，计算结果见表 2。1 000组数据的LTLS参数解和WTLS参数解与参数真值偏差的统计分析见图 1和图 2。
表 2 1000组实验的参数解均值和协因数阵Table 2. Average Parameter Values and Co⁃variance Matrix in 1 000 Experiments算法 参数解均值 协因数阵 $ {\rm{avg}} ( \hat{\boldsymbol{X}}_1) $ $ {\rm{avg}} ( \hat{\boldsymbol{X}}_2) $ $ {\boldsymbol{Q }}( \hat{\boldsymbol{X}} ) $ $ \bar{ \boldsymbol{Q }}( \hat{\boldsymbol{X}} ) $ LTLS算法 5.009 427 9.998 257 0.004 3 −0.005 1 0.004 2 −0.004 9 −0.005 1 0.007 3 −0.004 9 0.007 2 WTLS算法 5.009 427 9.998 257 0.004 3 −0.005 1 0.004 2 −0.004 9 −0.005 1 0.007 3 −0.004 9 0.007 2 ![]()
图 1 1 000组实验数据的LTLS参数解与参数真值偏差统计图Figure 1. Statistical Graph of Deviations Between Truth Values and Parameter Values Soluted by LTLS in 1 000 Experiments![]()
图 2 1 000组实验数据的WTLS参数解与参数真值偏差统计图Figure 2. Statistical Graph of Deviations Between Truth Values and Parameter Values Soluted by WTLS in 1 000 Experiments由表 2、图 1和图 2可以看出，LTLS算法与WTLS算法的统计结果完全一致，说明在每次实验中两种算法所求参数解均一致，验证了LTLS算法的正确性。同时两种计算协因数阵的方法结果非常相近，验证了参数协因数阵一阶近似估计公式（17）的有效性[17]。
3.2 实验2
为分析LTLS算法的计算效率，设计通用EIV模型中待估计量个数在不同的数量级情况，采用LTLS算法和WTLS算法计算100组模拟数据的平均迭代次数N、平均解算时间t和减少比例（LTLS算法较WTLS算法减少的平均解算时间与WTLS算法平均解算时间之比），结果见表 3。
表 3 LTLS算法和WTLS算法计算效率的比较Table 3. Comparison of Computational Efficiency Between LTLS Algorithm and WTLS Algorithm待估量数量 NLTLS NWTLS tLTLS tWTLS 减少比例/% 10 5.18 4.5 0.224 ms 0.191 ms − 100 5.04 6.36 0.681 ms 0.724 ms 5.9 1 000 5 6.75 0.033 s 0.044 s 25.0 10 000 5 7.5 2.681 s 3.909 s 31.4 从表 3可以看出，两种算法每次迭代的平均时间基本一致；当模型估计量数量较少时，两种算法的效率基本相当，随着估计量的数量级逐渐增大，LTLS算法的效率高于WTLS算法。原因在于GHM按泰勒级数展开后，仅包含常数项、一阶项（二阶及以上项全部为零），LTLS算法将二阶项纳入常数项，减小了线性化引起的模型误差，迭代计算收敛更快，迭代次数减少，使得计算效率提高。
3.3 实验3
本文采用的摄影测量实例示意图如图 3所示，由3个地面摄像机S1、S2和S3拍摄两个目标点P1和P2组成，相机主距f=100 mm，距离l1、l2、l3、l4、l5、l6、y1、y2的观测值和中误差见表 4。
表 4 距离观测值及其中误差Table 4. Distance Observations and Standard Deviations统计项 l1/mm l2/mm l3/mm l4/mm l5/mm l6/mm y1/m y2/m 观测值 14.1 16.6 6.1 7.1 22.1 26.3 10.0 8.0 中误差 0.10 0.10 0.10 0.10 0.10 0.10 0.05 0.05 根据图 3可得到误差方程：
$$ \left\{\begin{array}{l} l_{1} x_{2}-f x_{1}=0 \\ l_{2} x_{4}-f x_{3}=0 \\ l_{3} x_{2}+f y_{1}+f x_{1}=0 \\ l_{4} x_{4}+f y_{1}+f x_{3}=0 \\ l_{5} x_{2}-f y_{1}-f y_{2}+f x_{1}=0 \\ l_{6} x_{4}-f y_{1}-f y_{2}+f x_{3}=0 \end{array}\right. $$ (18) 构建通用EIV模型来估计点P1和点P2的坐标，由误差方程可得：
$$ \begin{array}{l} \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&0\\ { - f}&0\\ { - f}&0\\ { - f}&{ - f}\\ { - f}&{ - f} \end{array}} \right],\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} { - f}&{{l_1}}&0&0\\ 0&0&{ - f}&{{l_2}}\\ f&{{l_3}}&0&0\\ 0&0&f&{{l_4}}\\ f&{{l_5}}&0&0\\ 0&0&f&{{l_6}} \end{array}} \right],\\ \mathit{\boldsymbol{y}} = \left[ {\begin{array}{*{20}{l}} {{y_1}}\\ {{y_2}} \end{array}} \right],\mathit{\boldsymbol{x}} = \left[ {\begin{array}{*{20}{l}} {{x_1}}\\ {{x_2}}\\ {{x_3}}\\ {{x_4}} \end{array}} \right],\mathit{\boldsymbol{w}} = \left[ {\begin{array}{*{20}{l}} 0\\ 0\\ 0\\ 0\\ 0\\ 0 \end{array}} \right] \end{array} $$ (19) 由式（19）可知矩阵A不含有随机误差，则该矩阵的改正数矩阵为零矩阵。采用LTLS算法和WTLS算法解算，设置阈值为1×10-8，结果见表 5和表 6。两种方法所得坐标估值和距离观测值估值完全一致，该实例表示为通用EIV模型时系数矩阵中待估计量较少，所以两个算法收敛速度相差不大。
表 5 点P1和点P2的坐标估值/mTable 5. Coordinate Estimates of P1 and P2 /m算法 坐标估值 $ \hat x_1 $ $ \hat x_2 $ $ \hat x_3 $ $ \hat x_4 $ LTLS算法 6.995 056 5 49.715 632 6.981 465 5 41.968 315 9 WTLS算法 6.995 056 5 49.715 632 6.981 465 5 41.968 315 9 表 6 距离观测值估值Table 6. Estimation of Distance Observations算法 $ \hat l_1 $/mm $ \hat l_2 $/mm $ \hat l_3 $/mm $ \hat l_4 $/mm $ \hat l_5 $5/mm $ \hat l_6 $/mm $ \hat y_1 $/m $ \hat y_2 $/m LTLS算法 14.070 1 16.635 1 6.032 4 7.178 4 22.137 7 26.256 7 9.994 1 8.006 8 WTLS算法 14.070 1 16.635 1 6.032 4 7.178 4 22.137 7 26.256 7 9.994 1 8.006 8 4 结语
本文将通用EIV函数模型展开后的二阶项纳入模型的常数项，将通用EIV模型表示为线性形式的GHM，推导出通用EIV模型的线性化整体最小二乘算法和近似精度估计公式。实验结果表明，通用EIV模型的LTLS算法与WTLS算法结果一致，验证了该算法的正确性。此外，LTLS算法估计精度公式和WTLS估计精度公式均为一阶近似精度，因此两种算法参数的估计精度相同。当通用EIV模型的待估量数量较多时，LTLS算法比WTLS计算效率更高，在处理海量数据时更具有优势。
http://ch.whu.edu.cn/cn/article/doi/10.13203/j.whugis20220579
-
![]()
图 1 城市场景描述与人口分析单元关系
Figure 1. Relationship Between Urban Scene Description and Population Analysis Unit
![]()
图 2 融合城市场景组成要素的人口分析单元描述框架
Figure 2. Description Framework of Population Analysis Unit Integrating Elements of Urban Scene
![]()
图 3 城市场景与人口分析单元关联特征参考标准
Figure 3. Reference Standard for Correlation Features of Urban Scenes and Population Analysis Units
![]()
图 5 突发公共卫生事件场景空间结构和参考空间单元
Figure 5. Spatial Structure of Epidemic Scenarios and Reference Space Units
![]()
图 7 突发公共卫生事件功能区级场景摘要数据集和用地属性更新过程
Figure 7. The Process of Basic Description and Land Use Attribute Updating of Epidemic Functional Area Scenarios
![]()
图 8 突发公共卫生事件场景功能区级参考空间单元更新过程
Figure 8. Update Process of Functional Area-Level Reference Space Units in Epidemic Scenarios
![]()
图 9 人口分析单元属性动态更新过程示例
Figure 9. Example of Dynamic Updating Process of Population Analysis Unit Attributes
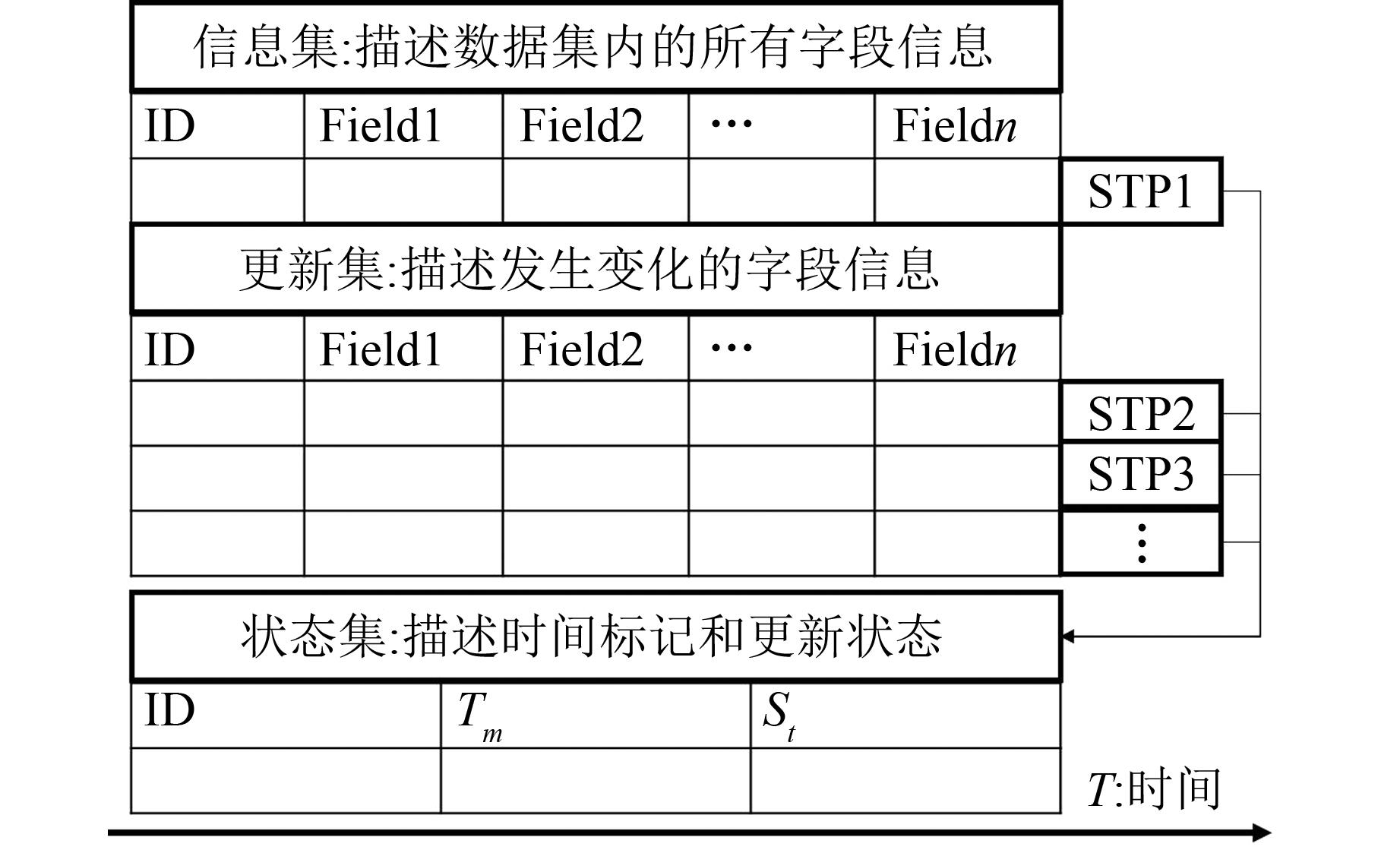
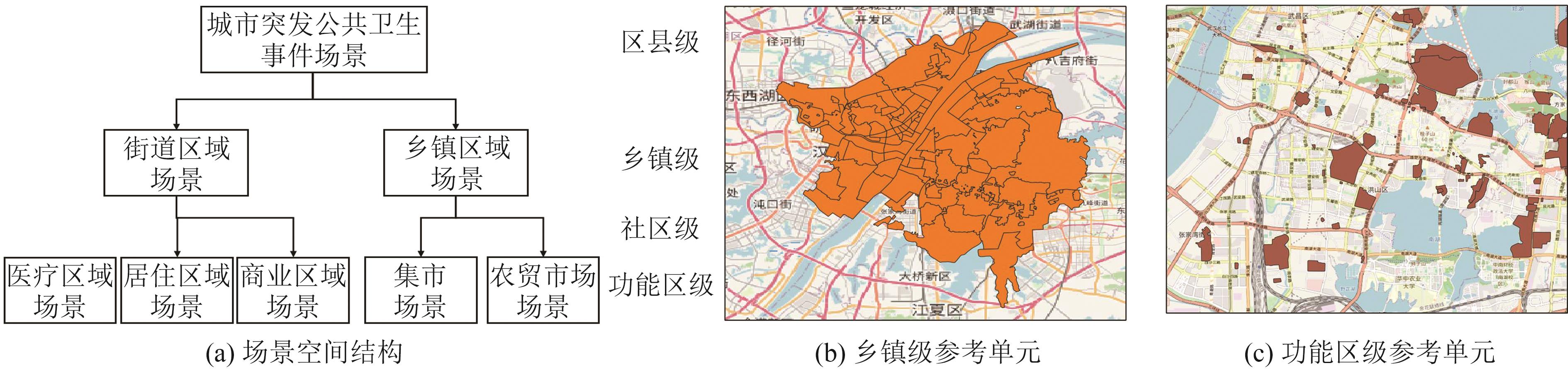
表 1 人口分析单元与多粒度时空对象对比
Table 1 Comparison of Population Analysis Units with Multi-granularity Spatiotemporal Objects
对比内容 共同点 多粒度时空对象 人口分析单元 概念定义 数字化描述和建模 每个对象有实体对应 人工虚拟构建或有对应实体,实质是对空间区域的划分与界定 时空参照 都存在时空参照标准,包括时间、空间、时空间参照变化,相应的描述和属性也会发生变化 空间形态 可视化表现形式 多形态（二维、三维） 二维 对象组成 都存在组成关系,可拆分,可组合 从简单对象到复杂对象,类型不一 二维的简单对象组合 关联关系 都存在关联关系：属性、空间、综合关联 认知能力 无 具有知识和自主决策能力 不存在认知能力 行为能力 时空分析、信息处理 复杂多维、细化宽泛 二维人口信息展示和分析：人口分布、变化、流动 属性特征 随着时空尺度动态变化 复杂多维的属性描述和知识参考 基于二维空间形态和人口活动区域的属性描述 
下载: 导出CSV
表 2 城市场景组成要素
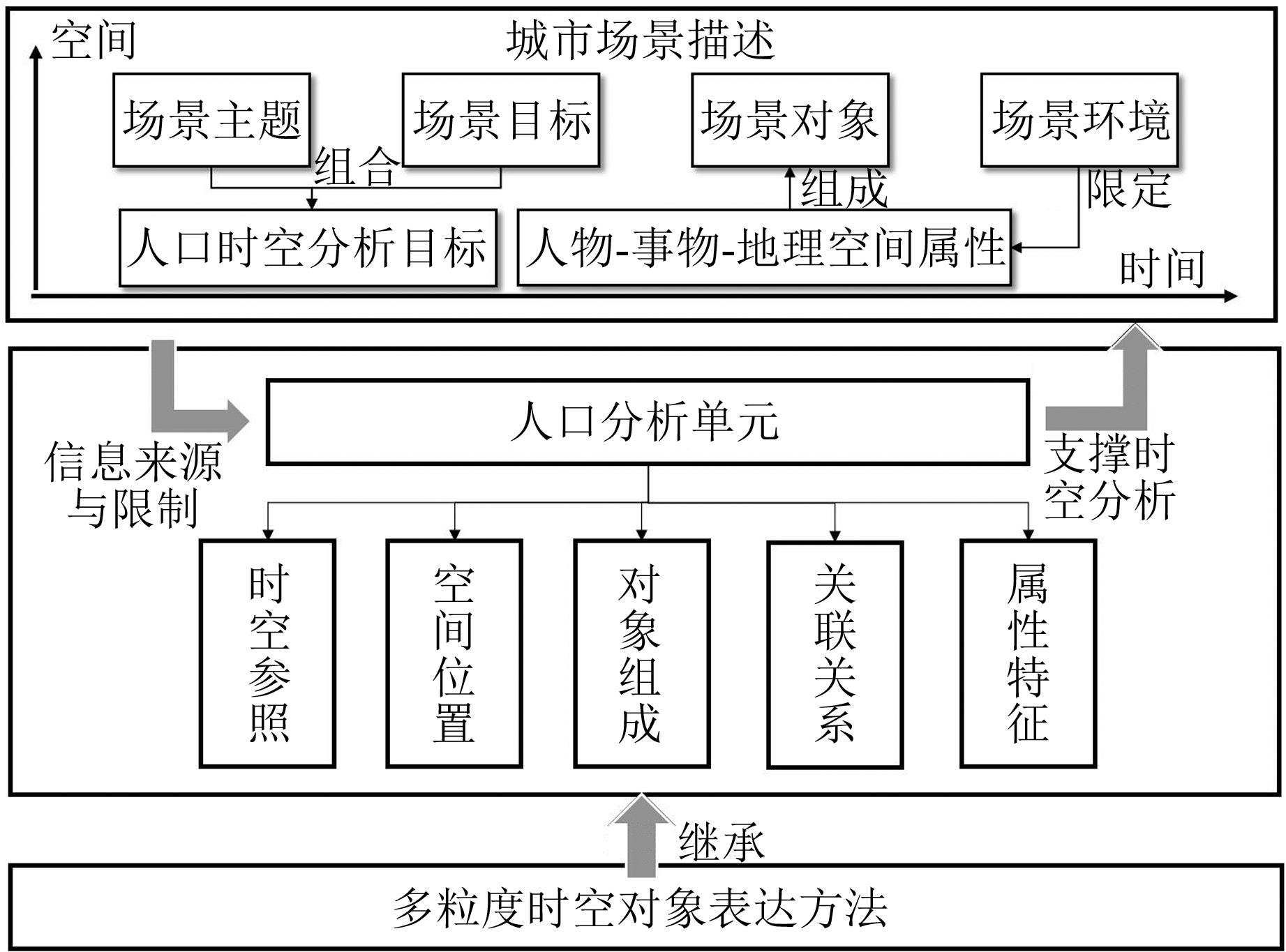
Table 2 Elements of an Urban Scene
场景组成要素 具体内容 举例 场景主题 人口活动问题的粗粒度描述,赋予人口分析实际意义和基本语义描述类型 日常通勤、交通出行、卫生医疗等 场景目标 场景主题下人口时空分析所需要获取的人口活动信息 人口属性（数量、密度）、活动模式、活动规律等 场景对象 场景中发生具体交互或存在关联关系的对象,具体可分为3类： 人物：进行时空活动的主体人群 如常住人口、活跃人口、老年人等 事物：与人群时空活动发生交互或者相关的其他要素 如建筑物、城市设施等 地理空间：人口时空活动所处的实际地理或空间区域 如封闭场所、功能区等 场景环境 基于场景主题,影响场景对象属性描述、交互或随时间变化而发生的一种特殊模式,包括两类： 人文环境：由人群或社会文化形成的环境 如节假日、赛事演出等 自然环境：由自然事物形成的环境 如天气、季节等
下载: 导出CSV
表 3 城市场景描述与人口分析单元表达关联分析
Table 3 Correlation Analysis Between Urban Scene Description and Population Analysis Unit Expression
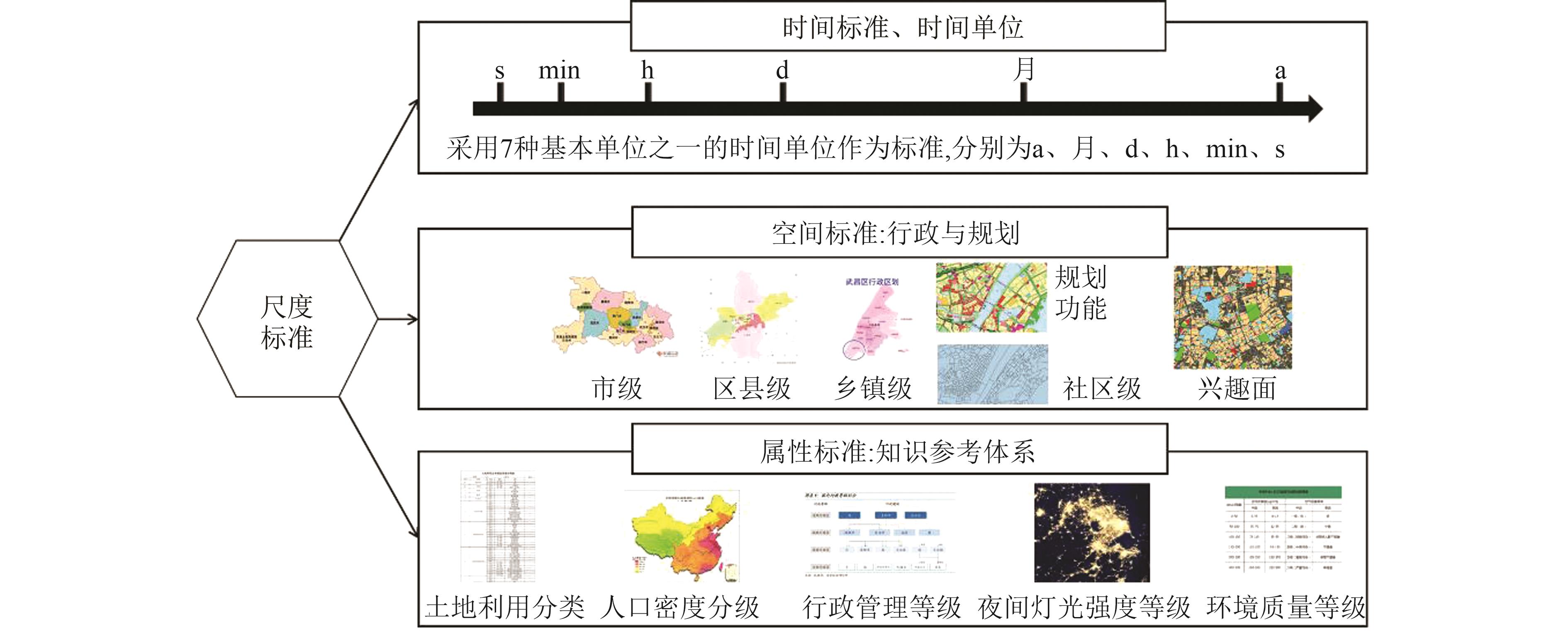
关联内容 人口分析单元 城市场景 需求与关联 定义 结构化对象表达 问题需求描述 对象服务于需求 时空参照 需要时空参照标准,包括时间、空间 对时间、空间参照模糊描述 空间主要参照WGS84或CGCS2000标准,时间参考北京时间 空间位置 描述单元在不同空间参照系中的具体位置和方向 城市场景存在对空间位置信息和尺度的语义描述 城市场景提供了空间位置的语义信息描述,如地名地址、场所或空间尺度等 组成结构 描述单元之间部分与整体的构成关系 不同场景可能具有层次关系,例如包含、组合、平行 同一主题的城市场景具有多层次特点,不同层次的场景对应不同尺度人口分析单元表达 关联关系 描述单元之间的相互影响关系内涵 不同场景存在的作用关系,包括时空间、属性等,由场景组成要素描述确定 城市场景描述提出了属性和时空间的参考标准需求 属性特征 描述单元的属性信息 对场景对象和环境的语义描述 场景对象的语义描述给人口分析单元的属性描述提供信息来源、属性字段和知识参考体系需求
下载: 导出CSV
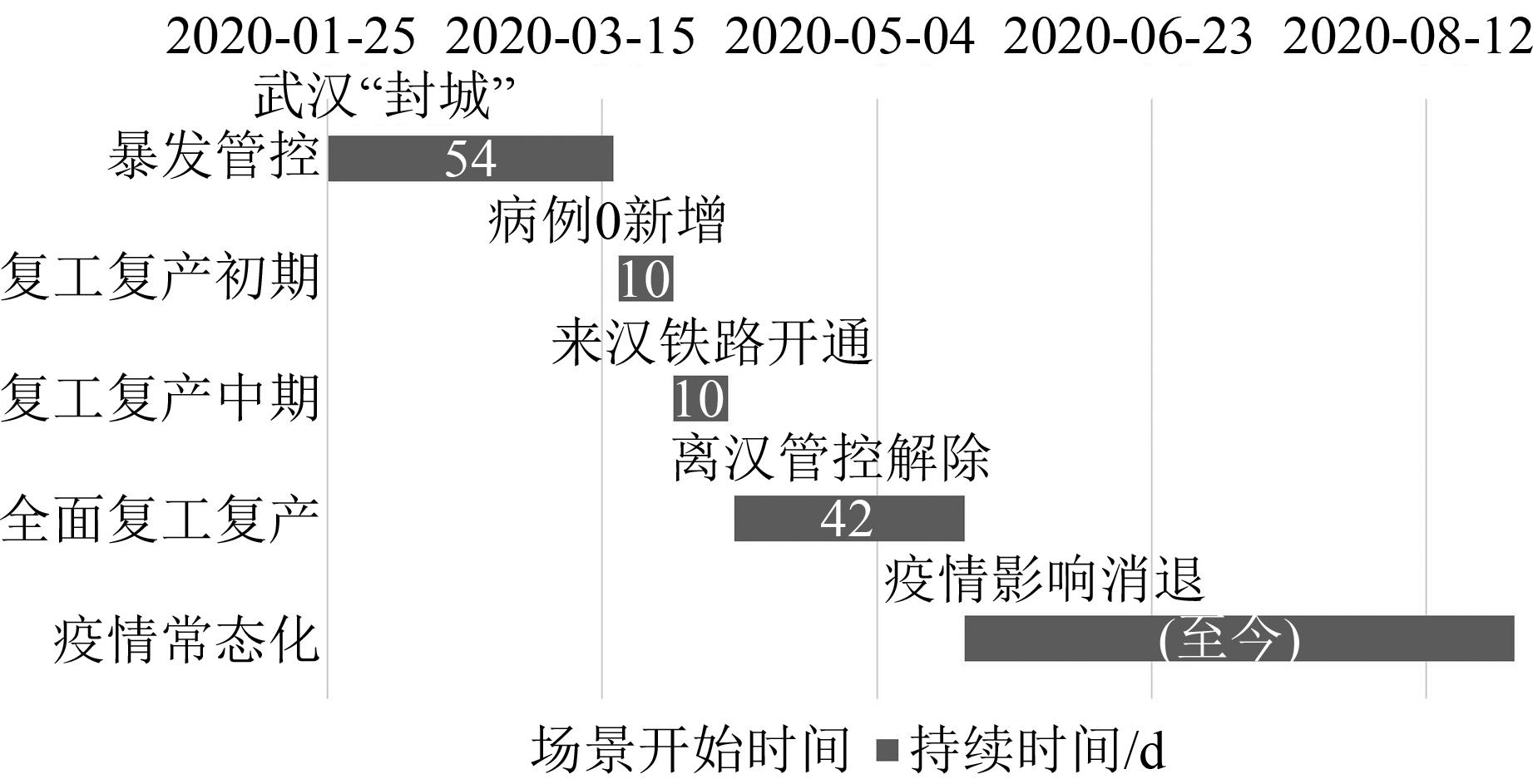
表 5 突发公共卫生事件防控场景案例研究数据
Table 5 Case Study Data of Epidemic Prevention and Control Scenarios
场景描述 具体内容 数据源 场景主题 主题类别、场景目标、人口分析目标等 突发公共卫生事件防控方案、突发公共卫生事件防控暂行办法、武汉市GIS数据、土地利用现状分类等属性标准 场景对象 场景对象属性 场景时间 场景发展历程 突发公共卫生事件防控方案、《抗击新冠肺炎疫情的中国行动》白皮书、突发公共卫生事件防控暂行办法、行政管理等级等 场景空间 场景发生空间范围 场景环境 场景包含的特殊事件和模式
下载: 导出CSV
-
[1] 刘盛和, 邓羽, 胡章. 中国流动人口地域类型的划分方法及空间分布特征[J]. 地理学报, 2010, 65（10）：1187-1197. Liu Shenghe, Deng Yu, Hu Zhang. Research on Classification Methods and Spatial Patterns of the Regional Types of China’s Floating Population[J]. Acta Geographica Sinica, 2010, 65（10）： 1187-1197.
[2] 刘耀林, 方飞国, 王一恒. 基于手机数据的城市内部就业人口流动特征及形成机制分析： 以武汉市为例[J]. 武汉大学学报（信息科学版）, 2018, 43（12）：2212-2224. Liu Yaolin, Fang Feiguo, Wang Yiheng. Characteristics and Formation Mechanism of Intra-urban Employment Flows Based on Mobile Phone Data：Taking Wuhan City as an Example[J]. Geomatics and Information Science of Wuhan University, 2018, 43（12）： 2212-2224.
[3] 姚尧, 张亚涛, 关庆锋, 等. 使用时序出租车轨迹识别多层次城市功能结构[J]. 武汉大学学报（信息科学版）, 2019, 44（6）：875-884. Yao Yao, Zhang Yatao, Guan Qingfeng, et al. Sensing Multi-level Urban Functional Structures by Using Time Series Taxi Trajectory Data[J]. Geomatics and Information Science of Wuhan University, 2019, 44（6）： 875-884.
[4] 郑宇. 城市计算概述[J]. 武汉大学学报（信息科学版）, 2015,40（1）：1-13. Zheng Yu. Introduction to Urban Computing[J]. Geomatics and Information Science of Wuhan University, 2015,40（1）：1-13.
[5] 吴京航, 桂志鹏, 申力, 等. 顾及格网属性分级与空间关联的人口空间化方法[J]. 武汉大学学报（信息科学版）, 2022, 47（9）：1364-1375. Wu Jinghang, Gui Zhipeng, Shen Li, et al. Population Spatialization by Considering Pixel-Level Attribute Grading and Spatial Association[J]. Geomatics and Information Science of Wuhan University, 2022, 47（9）： 1364-1375.
[6] Séguin A M, Apparicio P, Riva M. The Impact of Geographical Scale in Identifying Areas as Possible Sites for Area-Based Interventions to Tackle Poverty： The Case of Montréal[J]. Applied Spatial Analysis and Policy, 2012, 5（3）： 231-251.
[7] Zhou X G, Liu J Z, Yeh A G O, et al. The Uncertain Geographic Context Problem in Identifying Activity Centers Using Mobile Phone Positioning Data and Point of Interest Data[M]//Harvey F, Leung Y. AdvancesinSpatial Data Handling and Analysis. New York： Springer, 2015.
[8] Wang J, Kwan M P. An Analytical Framework for Integrating the Spatiotemporal Dynamics of Environmental Context and Individual Mobility in Exposure Assessment： A Study on the Relationship Between Food Environment Exposures and Body Weight[J]. International Journal of Environmental Research and Public Health, 2018, 15（9）： 2022.
[9] Kwan M P. The Uncertain Geographic Context Problem[J]. Annals of the Association of American Geographers, 2012, 102（5）： 958-968.
[10] Brown D G, Riolo R, Robinson D T, et al. Spatial Process and Data Models： Toward Integration of Agent-Based Models and GIS[J]. Journal of Geographical Systems, 2005, 7（1）： 25-47.
[11] Worboys M F, Hearnshaw H M, Maguire D J. Object-Oriented Data Modelling for Spatial Databases[J]. International Journal of Geographical Information Systems, 1990, 4（4）： 369-383.
[12] Worboys M F. A Unified Model for Spatial and Temporal Information[J]. The Computer Journal, 1994, 37（1）： 26-34.
[13] 宋玮. 时空数据模型及其在土地管理中的应用研究[D]. 郑州： 信息工程大学, 2005. Song Wei. Spatio-Temporal Data Model and Its Application in Land Management[D].Zhengzhou： Information Engineering University, 2005.
[14] 宋玮, 王家耀, 郭金华. 面向对象时空数据模型的研究[J]. 测绘科学技术学报, 2006, 23（4）：235-238. Song Wei, Wang Jiayao, Guo Jinhua. An Object-Oriented Spatial-Temporal Data Model[J]. Journal of Geomatics Science and Technology, 2006, 23（4）： 235-238.
[15] 朱杰, 张宏军. 面向仿真事件的战场地理环境时空过程建模[J]. 武汉大学学报（信息科学版）, 2020, 45（9）： 1367-1377. Zhu Jie, Zhang Hongjun. Battlefield Geographic Environment Spatiotemporal Process Model Based on Simulation Event[J]. Geomatics and Information Science of Wuhan University, 2020, 45（9）： 1367-1377.
[16] 吴长彬, 闾国年. 一种改进的基于事件-过程的时态模型研究[J]. 武汉大学学报（信息科学版）, 2008, 33（12）： 1250-1253. Wu Changbin, Guonian Lü. Improved Event-Process Based on Spatiotemporal Model[J].Geomatics and Information Science of Wuhan University, 2008, 33（12）： 1250-1253.
[17] 孟令奎, 赵春宇, 林志勇, 等. 基于地理事件时变序列的时空数据模型研究与实现[J]. 武汉大学学报（信息科学版）, 2003, 28（2）： 202-207. Meng Lingkui, Zhao Chunyu, Lin Zhiyong, et al. Research and Implementation of Spatiotemporal Data Model Based on Time-Varying Sequence of Geographical Events[J]. Geomatics and Information Science of Wuhan University, 2003, 28（2）： 202-207.
[18] 苏奋振, 周成虎. 过程地理信息系统框架基础与原型构建[J]. 地理研究, 2006, 25（3）： 477-484. Su Fenzhen, Zhou Chenghu. A Framework for Process Geographical Information System[J].Geographical Research, 2006, 25（3）： 477-484.
[19] 朱杰, 游雄, 夏青. 基于任务过程的战场环境对象时空数据组织模型[J]. 武汉大学学报（信息科学版）, 2018, 43（11）： 1739-1745. Zhu Jie, You Xiong, Xia Qing. Battlefield Environment Object Spatiotemporal Data Organizing Model Based on Task-Process[J].Geomatics and Information Science of Wuhan University, 2018, 43（11）： 1739-1745.
[20] Chen B Y, Yuan H, Li Q Q, et al. Spatiotemporal Data Model for Network Time Geographic Analysis in the Era of Big Data[J]. International Journal of Geographical Information Science, 2016, 30（6）： 1041-1071.
[21] Camossi E, Bertolotto M, Bertino E, et al. A Multigranular Spatiotemporal Data Model[C]//The 11th ACM International Symposium on Advances in Geographic Information Systems, New Orleans Louisiana, USA, 2003.
[22] Camossi E, Bertolotto M, Bertino E. A Multigranular Object-Oriented Framework Supporting Spatiotemporal Granularity Conversions[J]. International Journal of Geographical Information Science, 2006, 20（5）： 511-534.
[23] 华一新, 周成虎. 面向全空间信息系统的多粒度时空对象数据模型描述框架[J]. 地球信息科学学报, 2017, 19（9）：1142-1149. Hua Yixin, Zhou Chenghu. Description Frame of Data Model of Multi-granularity Spatiotemporal Object for Pan-Spatial Information System[J]. Journal of Geo-Information Science, 2017, 19（9）： 1142-1149.
[24] 刘朝辉, 李锐, 王璟琦. 顾及语义尺度的时空对象属性特征动态表达[J]. 地球信息科学学报, 2017, 19（9）：1185-1194. Liu Zhaohui, Li Rui, Wang Jingqi. A Dynamic Representation Method of Considering Semantic Scales of Attributes of Spatiotemporal Object[J]. Journal of Geo-Information Science, 2017, 19（9）： 1185-1194.
[25] 李锐, 石佳豪, 董广胜, 等. 多粒度时空对象组成结构表达研究[J]. 地球信息科学学报, 2021, 23（1）： 113-123. Li Rui, Shi Jiahao, Dong Guangsheng, et al. Research on Expression of Multi-granularity Spatio-Temporal Object Composition Structure[J].Journal of Geo-Information Science, 2021, 23（1）： 113-123.
[26] 刘凯, 毋河海, 艾廷华, 等. 地理信息尺度的三重概念及其变换[J]. 武汉大学学报 （ 信息科学版）, 2008, 33（11）： 1178-1181. Liu Kai, Wu Hehai, Ai Tinghua, et al. Three-Tiered Concepts of Scale of Geographical Information and Its Transformation[J].Geomatics and Information Science of Wuhan University, 2008, 33（11）： 1178-1181.
[27] Lü G, Batty M, Strobl J, et al. Reflections and Speculations on the Progress in Geographic Information Systems （GIS）： A Geographic Perspective[J]. International Journal of Geographical Information Science, 2019, 33（2）： 346-367.
[28] Lü G, Chen M, Yuan L W, et al. Geographic Scenario： A Possible Foundation for Further Development of Virtual Geographic Environments[J]. International Journal of Digital Earth, 2018, 11（4）： 356-368.
[29] Biehl A, Ermagun A, Stathopoulos A. Community Mobility MAUPing： A Socio-spatial Investigation of Bikeshare Demand in Chicago[J]. Journal of Transport Geography, 2018, 66： 80-90.
[30] 边馥苓, 杜江毅, 孟小亮. 时空大数据处理的需求、应用与挑战[J]. 测绘地理信息, 2016, 41（6）：1-4. Bian Fuling, Du Jiangyi, Meng Xiaoliang. Requirements,Applications and Challenges of Spatiotemporal Big Data Processing[J]. Journal of Geomatics, 2016, 41（6）： 1-4.
[31] Wu C S, Murray A T. A Cokriging Method for Estimating Population Density in Urban Areas[J]. Computers,Environment and Urban Systems, 2005, 29（5）： 558-579.
[32] Wong D W S. The Modifiable Areal Unit Problem （MAUP）[M]//Janelle D G, Warf B, Hansen K. WorldMinds： Geographical Perspectives on 100 Problems. Dordrecht： Springer, 2004.
[33] 段世江.论人口社会化[J].人口与经济,2004（S1）：24-26. Duan Shijiang. On Population Socialization[J]. Population & Economics,2004（S1）：24-26.
[34] 崔珂瑾, 程昌秀. 空间数据模型研究综述[J]. 地理信息世界, 2013,20（3）： 31-38. Cui Kejin, Cheng Changxiu. Research Review on Spatial Data Models[J].Geomatics World, 2013, 20（3）： 31-38.
[35] 周成虎. 全空间地理信息系统展望[J]. 地理科学进展, 2015,34（2）：129-131. Zhou Chenghu. Prospects on Pan-Spatial Information System[J]. Progress in Geography, 2015,34（2）：129-131.
[36] 华一新. 全空间信息系统的核心问题和关键技术[J]. 测绘科学技术学报, 2016, 33（4）：331-335. Hua Yixin. The Core Problems and Key Technologies of Pan-Spatial Information System[J]. Journal of Geomatics Science and Technology, 2016, 33（4）： 331-335.
[37] 杨超, 杨柳松, 杜阳,等.融合图像和时空信息的社交媒体用户活动分类方法[J]. 武汉大学学报（信息科学版）,2023,48（3）：463-470. Yang Chao, Yang Liusong, Du Yang, et al. Social Media User’s Activity Classification Integrating Image and Spatiotemporal Information[J]. Geomatics and Information Science of Wuhan University, 2023, 48（3）： 463-470.
[38] 张颖. 略谈戏剧和影视艺术中的叙事性场景[J]. 新世纪剧坛, 2018（5）：54-58. Zhang Yin. A Brief Discussion of Narrative Scenes in Drama and Film Art[J]. New Century Theatre, 2018（5）：54-58.
[39] 方志祥, 倪雅倩, 黄守倩. 融合Markov与多类机器学习模型的个体出行位置预测模型[J]. 武汉大学学报（信息科学版）, 2021, 46（6）： 799-806. Fang Zhixiang, Ni Yaqian, Huang Shouqian. A Multi-model Fusion Model of Individual Travel Location Prediction Using Markov and Machine Learning Methods[J]. Geomatics and Information Science of Wuhan University, 2021, 46（6）： 799-806.
[40] 吕峥, 孙群, 赵国成, 等. 顾及方向关系的农村居民地聚类方法[J]. 武汉大学学报（信息科学版）, 2023, 48（4）： 631-638. Zheng Lü, Sun Qun, Zhao Guocheng, et al. A Clustering Method of Rural Settlement Considering Direction Relation[J]. Geomatics and Information Science of Wuhan University, 2023, 48（4）： 631-638.
[41] 黄毅. 地理场景数据模型构建与本体表达[D]. 南京： 南京师范大学, 2020. Huang Yi. Construction of Geographic Scene Data Model and Ontology Representation[D].Nanjing： Nanjing Normal University, 2020.
[42] 曹天邦. 南京市主城区住宅地价时空演变及其影响因素研究[D]. 南京： 南京师范大学, 2013. Cao Tianbang. Spatial-Temporal Evolution of Residential Land Price in Nanjing Urban Area and Its Influencing Factors[D].Nanjing： Nanjing Normal University, 2013.
[43] 邓楚雄, 李晓青, 向云波, 等. 长株潭城市群地区耕地数量时空变化及其驱动力分析[J]. 经济地理, 2013,33（6）：142-147. Deng Chuxiong, Li Xiaoqing, Xiang Yunbo, et al. The Spatiotemporal Change and Driving Forces of Cultivated Land Quantity in Chang-Zhu-Tan Urban Agglomeration[J]. Economic Geography, 2013,33（6）：142-147.
[44] 魏迪, 厉旭宏. 我国“两级政府、三级管理”体制的法理质疑与完善选择[J]. 上海城市管理职业技术学院学报, 2007, 16（2）： 71-74. Wei Di, Li Xuhong. Jurisprudence Query and Perfect Choice of China's “Two-Level Government and Three-Level Management” System[J].Shanghai Urban Management, 2007, 16（2）： 71-74.
[45] 胡玲玲. “陌人社会”中社区共同体的重建[J]. 淮海工学院学报（人文社会科学版）, 2015, 13（9）： 105-107. Hu Lingling. Community Reconstruction in a “Strangers’ Society”[J].Journal of Jiangsu Ocean University （Humanities & Social Sciences Edition）, 2015, 13（9）： 105-107.
[46] 周国磊, 李诚固, 张婧, 等. 2003年以来长春市城市功能用地演替[J]. 地理学报, 2015, 70（4）：539-550. Zhou Guolei, Li Chenggu, Zhang Jing, et al. Transition of Urban Functional Land in Changchun from 2003 to 2012[J]. Acta Geographica Sinica, 2015, 70（4）： 539-550.
[47] Jendryke M. Inferring Shanghai’s Urban Vibrancy Using Microwave Remote Sensing and Big Social Sensing Data[D].Wuhan：Wuhan University, 2016.
[48] 许小可, 文成, 张光耀, 等. 新冠肺炎暴发前期武汉外流人口的地理去向分布及影响[J]. 电子科技大学学报, 2020,49（3）：324-329. Xu Xiaoke, Wen Cheng, Zhang Guangyao, et al. The Geographical Destination Distribution and Effect of Outflow Population of Wuhan When the Outbreak of COVID-19[J]. Journal of University of Electronic Science and Technology of China, 2020,49（3）：324-329.
-
期刊类型引用(6)
1. 杨根新，王友昆，谢正明. 基于广义EIV模型的矿区高程异常的无缝推估算法. 工程勘察. 2023(08): 46-51 . 
百度学术
2. Jianjun ZHU，Leyang WANG，Jun HU，Bofeng LI，Haiqiang FU，Yibin YAO. Recent Advances in the Geodesy Data Processing. Journal of Geodesy and Geoinformation Science. 2023(03): 33-45 . 必应学术
3. 翁烨，陈丽，王岩. 线性化通用EIV平差模型的正则化解法. 勘察科学技术. 2023(05): 1-5 . 百度学术
4. 戴中东，孟良，高永攀，项伟. 加权整体最小二乘坐标匹配算法在机场道面测量中的应用. 测绘地理信息. 2022(02): 61-66 . 百度学术
5. 翁烨，邵德盛，甘淑. 线性化通用EIV平差模型的岭估计解法. 全球定位系统. 2022(02): 82-89 . 百度学术
6. 翁烨，邵德盛. 病态加权总体最小二乘的广义岭估计解法. 全球定位系统. 2021(06): 84-89 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 312
- HTML全文浏览量: 40
- PDF下载量: 97
- 被引次数: 8
