不等式约束下加乘性混合误差模型的简单迭代解法

王乐洋; 韩澍豪

doi:10.13203/j.whugis20210659

不等式约束下加乘性混合误差模型的简单迭代解法

王乐洋^{1, 2,},
韩澍豪^{1, 2}

1.
东华理工大学测绘工程学院,江西南昌,330013
2.
自然资源部环鄱阳湖区域矿山环境监测与治理重点实验室,江西南昌,330013

基金项目:

国家自然科学基金 42174011

国家自然科学基金 41874001

详细信息

作者简介:
王乐洋,博士,教授,研究方向为大地测量反演及大地测量数据处理。wleyang@163.com

中图分类号: P207
计量
- 文章访问数: 891
- HTML全文浏览量: 107
- PDF下载量: 54
出版历程
- 收稿日期: 2022-04-02
- 网络出版日期: 2022-05-19
- 刊出日期: 2024-06-04

A Simple Iterative Solution for Mixed Additive and Multiplicative Random Error Model with Inequality Constraints

WANG Leyang^{1, 2,},
HAN Shuhao^{1, 2}

1.
Faculty of Geomatics, East China University of Technology, Nanchang330013, China
2.
Key Laboratory of Mine Environmental Monitoring and Improving Around Poyang Lake, Ministry of Natural Resources,Nanchang330013, China

摘要

摘要:
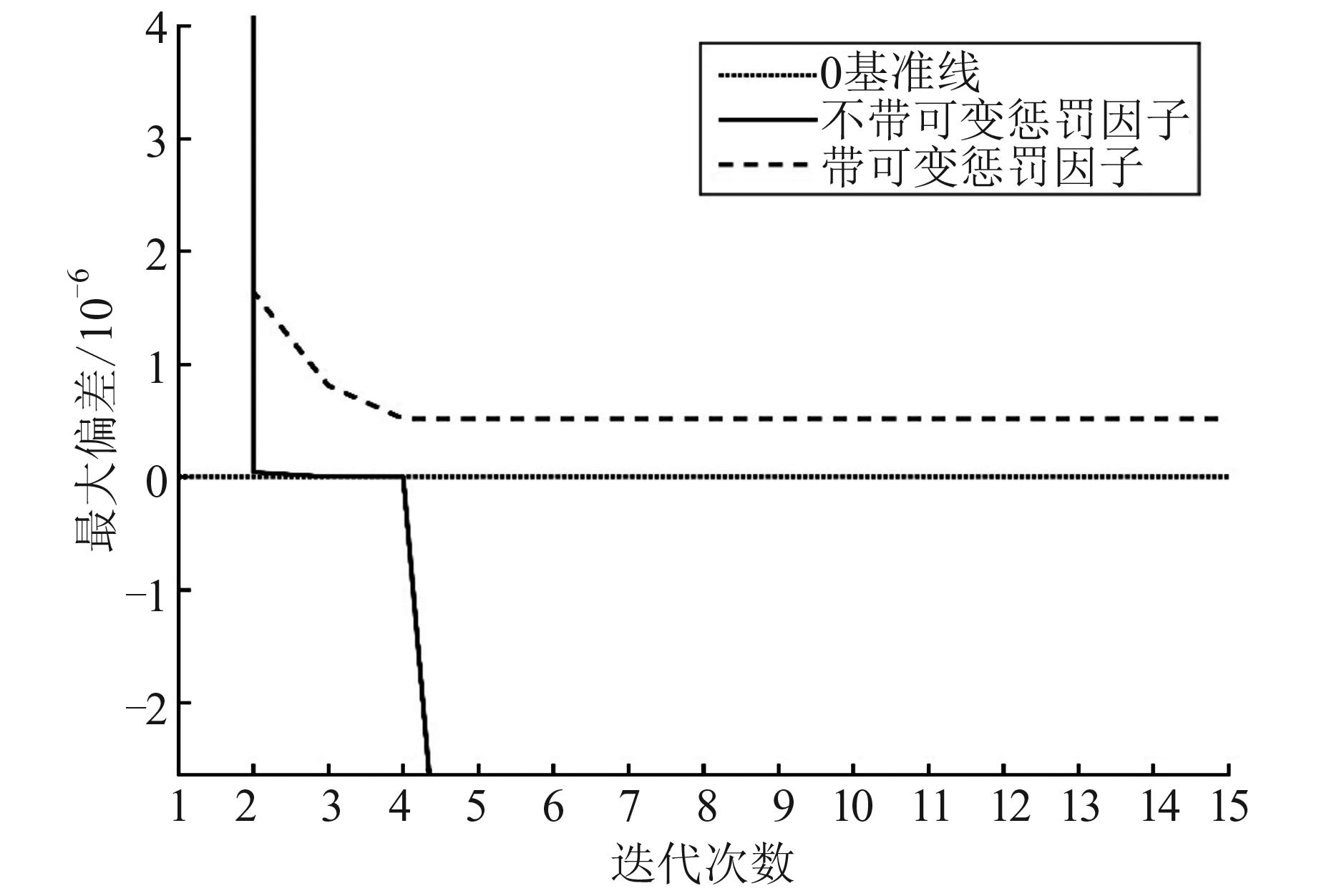
在大地测量领域中,现有的处理不等式约束的方法大多都是基于加性误差的模型,包括高斯马尔可夫模型和变量误差模型,鲜有对于加乘性混合误差模型处理方法的研究。为了拓展附有不等式约束的加乘性混合误差的方法,基于最小二乘原理并应用零权和无限权的思想,通过约束条件构建了惩罚函数,推导了在不等式约束下加乘性混合误差的一种简单迭代解法,分析了简单迭代解法在加乘性混合误差模型中的缺陷,在原有方法的基础上在惩罚项前加入了一个随迭代次数增加而增加的惩罚因子。通过算例评估分析可知,改进后的简单迭代法能够有效解决原有方法用于处理附有不等式约束的加乘性混合误差模型时不收敛的问题。通过对比其他方案可知,所提方法能够得到更好的参数估值,证明了该方法的有效性。同时,所提方法结构简单,易于实现,能够适用于大批量的数据处理。
- 加乘性混合误差模型 /
- 不等式约束 /
- 迭代解法 /
- 惩罚函数 /
- 惩罚因子
Abstract:
Objectives
With the development of modern observation techniques, the processing methods which only consider additive errors cannot meet the requirements. Most of the existing methods for dealing with inequality constraints are based on additive error models, including Gaussian-Markov model and errors-in-variables model, while the processing methods for mixed additive and multiplicative (MAM) random error models are rare.
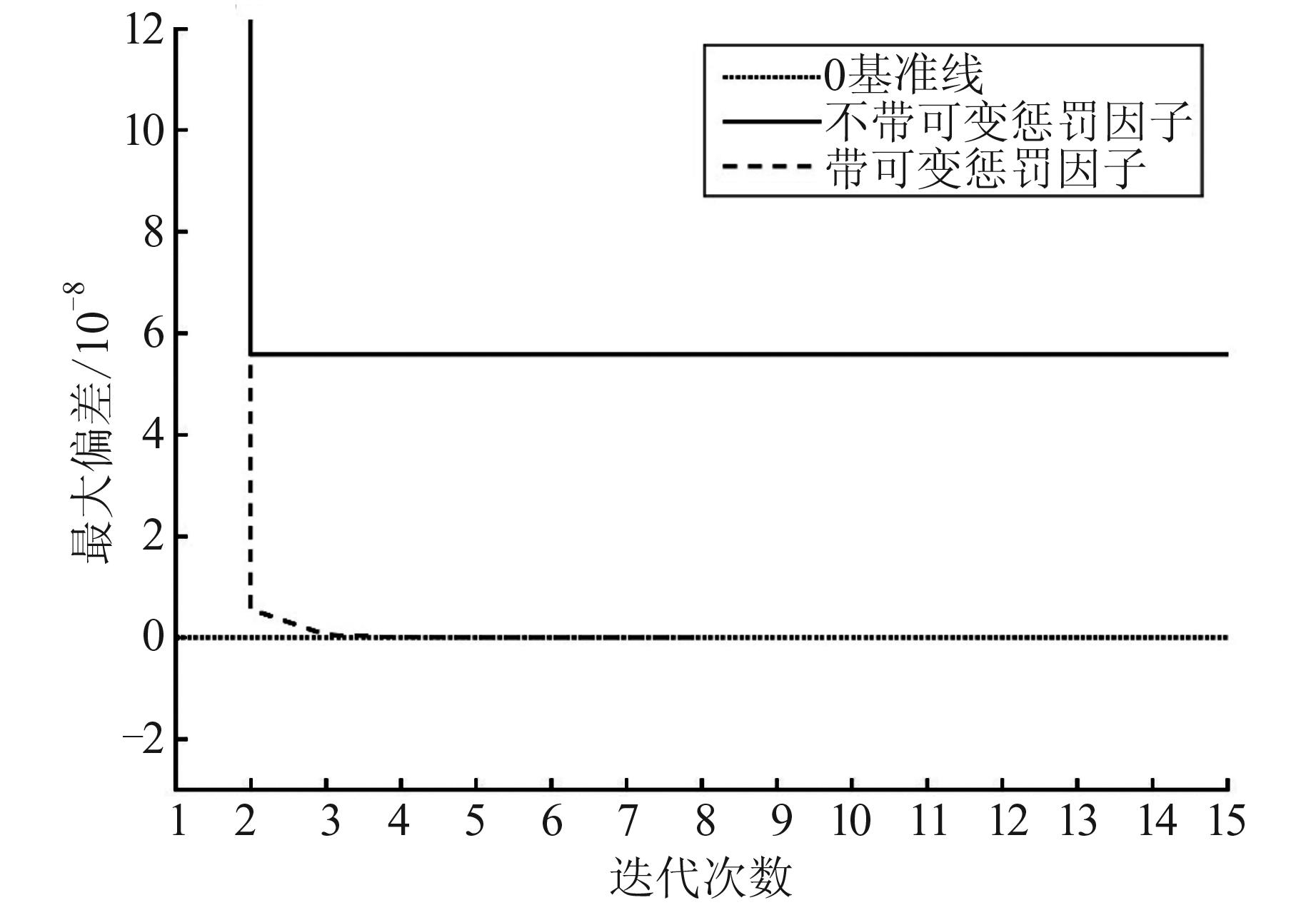
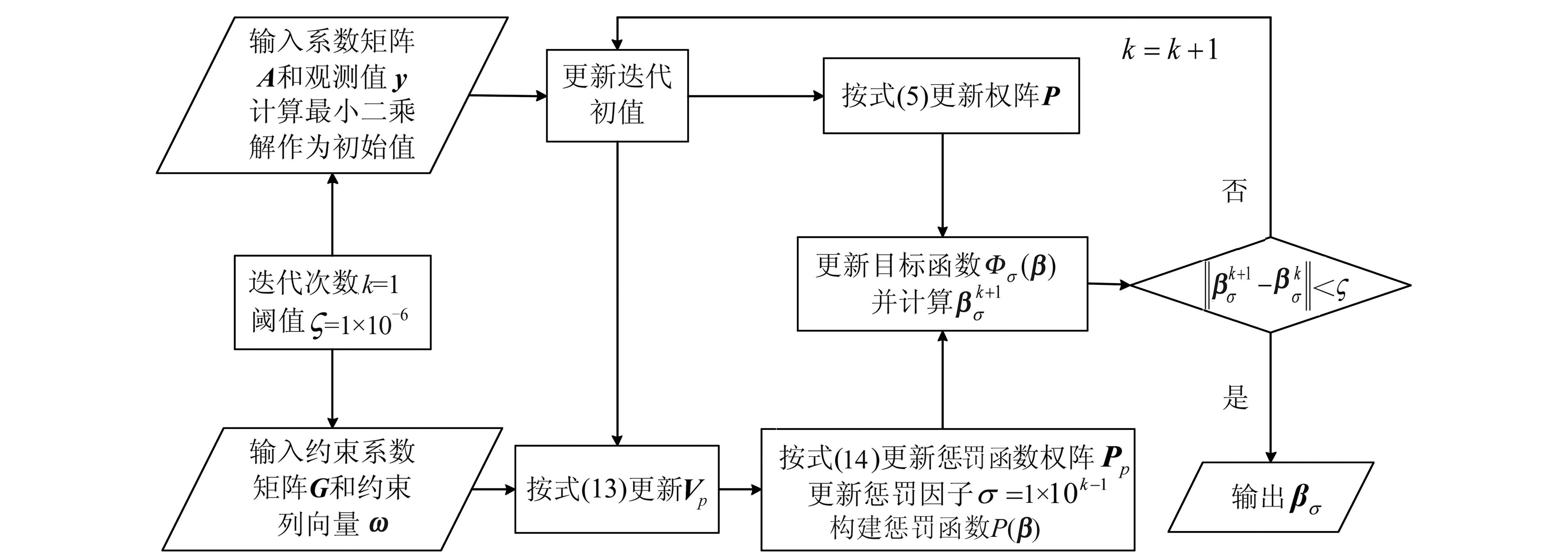
Methods
Based on the least squares principle and the ideas of zero and infinite weights, we construct a penalty function with the given inequality constraints, and derive the simple iterative method (SIM) for the estimation of MAM parameters under the inequality constraints. Then, we add a penalty factor increasing with the number of iterations before the penalty term to address the defects of the original SIM.
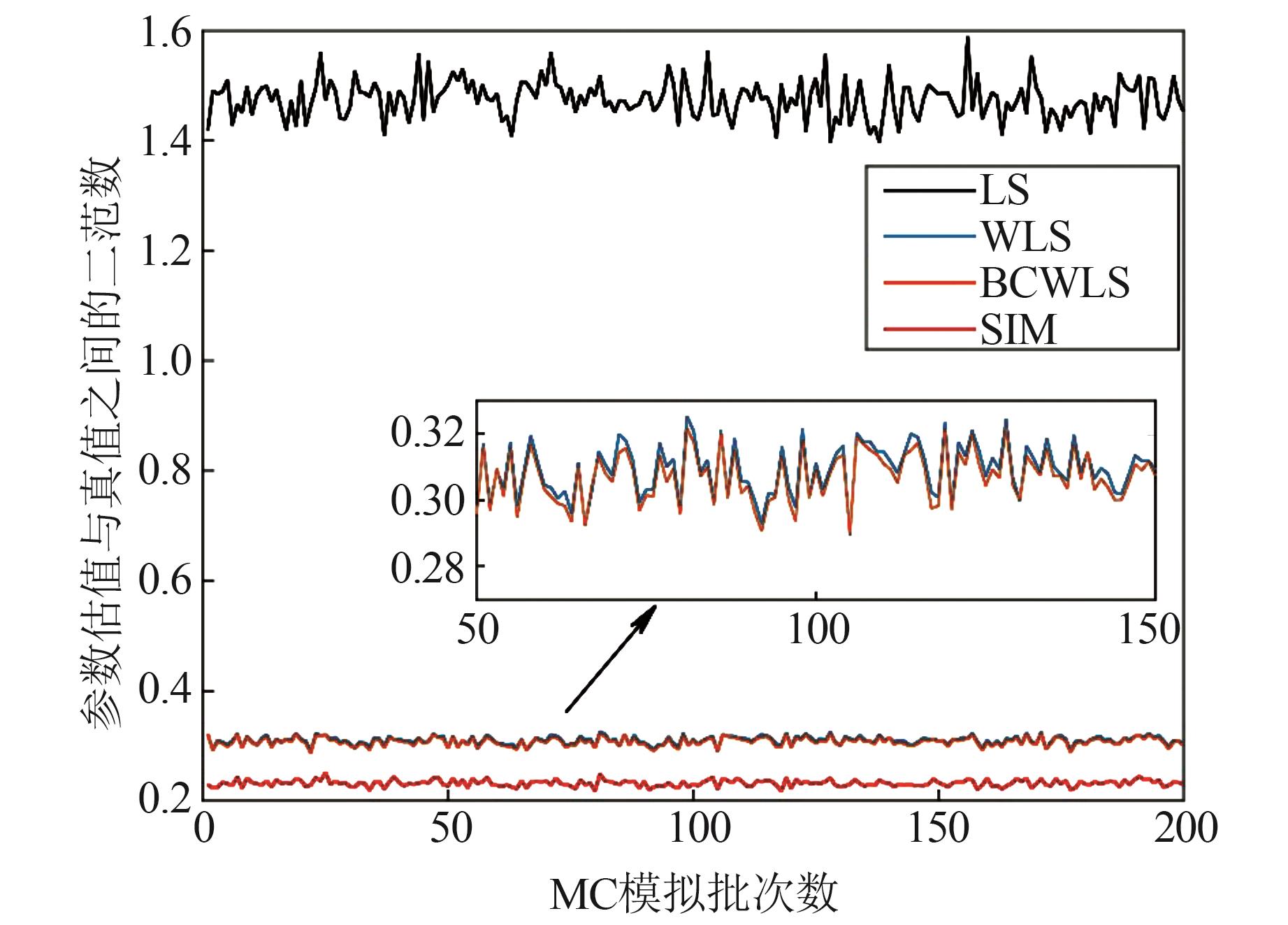
Results
Two sets of cases show that the improved SIM can effectively solve the problem that the original method does not converge when used to deal with MAM error models with inequality constraints. The structure of improved SIM is simple and easy to implement. And it can obtain better parameter estimation compared with other schemes.
Conclusions
The feasibility and effectiveness of the improved SIM for parameter estimation of MAM error models with inequality constraints are verified, and it can be applied to the processing of large batches of data.
- mixed additive and multiplicative random error model /
- inequality constraints /
- iterative solution /
- penalty function /
- penalty factor
http://ch.whu.edu.cn/cn/article/doi/10.13203/j.whugis20210659

HTML全文

http://ch.whu.edu.cn/cn/article/doi/10.13203/j.whugis20210659

图 1 算法流程图

Figure 1. Algorithm Flowchart

下载: 全尺寸图片幻灯片

图 2 未受影响的直线与受加乘性混合误差影响的坐标点

Figure 2. Unaffected Lines and Coordinate Points Affected by Mixed Additive and Multiplicative Random Errors

下载: 全尺寸图片幻灯片

图 3 惩罚因子对算法结果的影响

Figure 3. Influence of Penalty Factor on Algorithm Results

下载: 全尺寸图片幻灯片

图 4 4种方法在各批次中的二范数

Figure 4. 2-Norm of Four Methods in Each Batch

下载: 全尺寸图片幻灯片

图 5 未受影响和受加乘性混合误差影响的DEM

Figure 5. Unaffected and Affected by Mixed Additive and Multiplicative Error of DEM

下载: 全尺寸图片幻灯片

图 6 惩罚因子对算法结果的影响（算例2⁃2）

Figure 6. Influence of Penalty Factor on Algorithm Results (Case 2⁃2)

下载: 全尺寸图片幻灯片

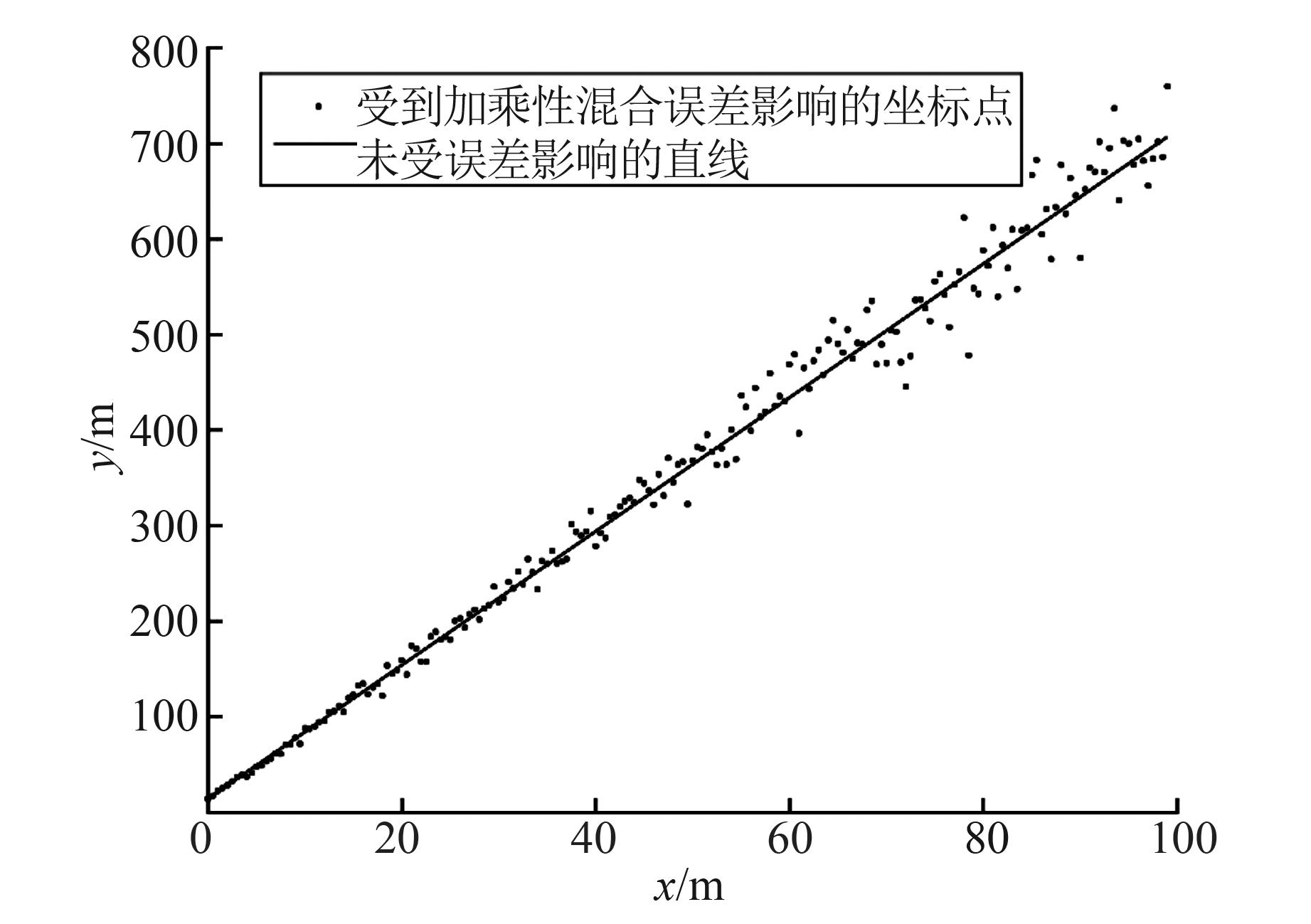
表 1 4种方法直线拟合的参数估值结果（算例1）

Table 1 Parameter Estimation Results of Four Methods(Case 1)

方案	${\hat{β}}_{1}$ /m	${\hat{β}}_{2}$ /m	$‖Δ β‖$
LS	6.99	15.172	1.172
WLS	7.032	14.348	0.349
BCWLS	7.013	14.334	0.334
SIM	7.041	14.168	0.173
真值	7	14	—

下载: 导出CSV

表 2 4种方法的参数估计结果（算例2⁃1）

Table 2 Parameter Estimation Results of Four Methods (Case 2-1)

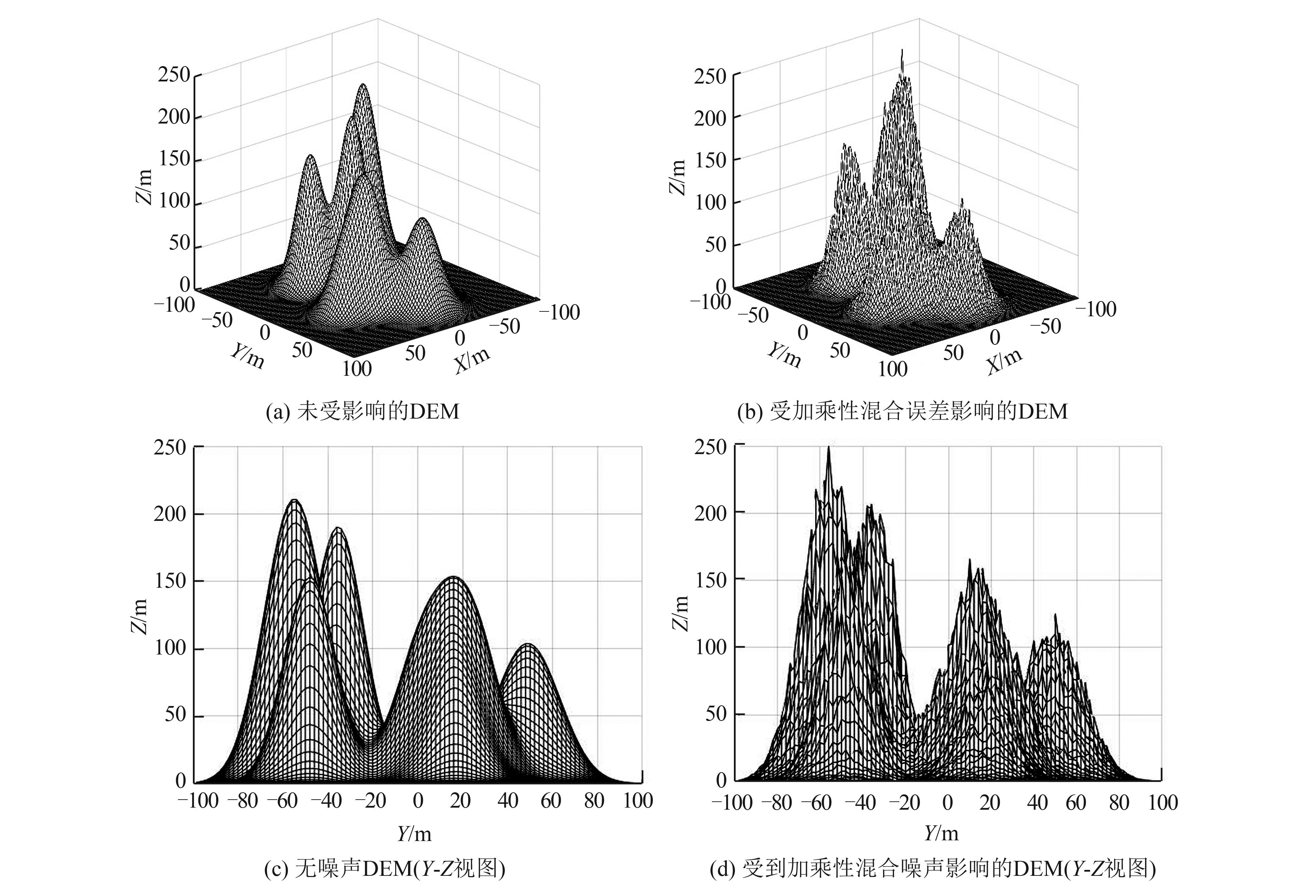
方法	${\hat{β}}_{1}$ /m	${\hat{β}}_{2}$ /m	${\hat{β}}_{3}$ /m	${\hat{β}}_{4}$ /m	${\hat{β}}_{5}$ /m	${\hat{β}}_{6}$ /m	${\hat{β}}_{7}$ /m	${\hat{β}}_{8}$ /m	$‖Δ β‖$
LS	104.327	76.903	83.840	68.889	186.532	65.938	210.453	152.266	10.677
WLS	105.042	76.965	85.477	70.860	187.218	66.574	211.900	152.875	9.301
BCWLS	104.101	76.406	84.684	70.002	185.479	65.996	210.037	151.624	9.240
SIM	104.291	75.124	84.744	73.751	187.708	64.654	209.406	153.955	6.889
真值	104.000	75.000	85.000	79.000	184.000	66.000	210.000	152.000	—

下载: 导出CSV

表 3 4种方法的参数估计结果（算例2⁃2）

Table 3 Parameter Estimation Results of Four Methods (Case 2-2)

方法	${\hat{β}}_{1}$ /m	${\hat{β}}_{2}$ /m	${\hat{β}}_{3}$ /m	${\hat{β}}_{4}$ /m	${\hat{β}}_{5}$ /m	${\hat{β}}_{6}$ /m	${\hat{β}}_{7}$ /m	${\hat{β}}_{8}$ /m	$‖Δ β‖$
LS	104.111	71.214	85.912	71.166	184.878	66.128	209.400	153.363	8.919
WLS	105.549	73.608	85.934	71.987	185.743	66.627	212.135	153.546	8.048
BCWLS	104.495	72.892	85.104	71.264	184.039	65.883	209.852	152.134	8.037
SIM	105.266	73.072	85.457	72.166	183.790	66.719	211.469	152.712	7.447
真值	104.000	75.000	85.000	79.000	184.000	66.000	210.000	152.000	—

下载: 导出CSV

参考文献(23)

[1]	Rodriguez E, Martin J M. Theory and Design of Interferometric Synthetic Aperture Radars[J]. IEEE Proceedings of Radar and Signal Processing, 1992, 139（2）： 147.
[2]	吴星辉, 马海涛, 张杰. 地基合成孔径雷达的发展现状及应用[J]. 武汉大学学报（信息科学版）, 2019, 44（7）： 1073-1081. Wu Xinghui, Ma Haitao, Zhang Jie. Development Status and Application of Ground-Based Synthetic Aperture Radar[J]. Geomatics and Information Science of Wuhan University, 2019, 44（7）： 1073-1081.
[3]	贾燕, 金双根, 肖智宇, 等. 全球导航卫星系统反射测量土壤水分遥感：现状与机遇[J]. 武汉大学学报（信息科学版）, 2023, 48（11）： 1784-1799. Jia Yan, Jin Shuanggen, Xiao Zhiyu, et al. Soil Moisture Remote Sensing Using Global Navigation Satellite System-Reflectometry： Current Status and Opportunity[J]. Geomatics and Information Science of Wuhan University, 2023, 48（11）： 1784-1799.
[4]	Schilizzi R T. Very Long Baseline Interferometry[J]. Radio Science, 1986, 21（4）： 665-679.
[5]	Xu P L. Despeckling SAR-Type Multiplicative Noise[J]. International Journal of Remote Sensing, 1999, 20（13）： 2577-2596.
[6]	Painam R K, Manikandan S. A Comprehensive Review of SAR Image Filtering Techniques： Systematic Survey and Future Directions[J]. Arabian Journal of Geosciences, 2021, 14（1）： 37.
[7]	Lin Q, Allebach J P. Combating Speckle in SAR Images： Vector Filtering and Sequential Classification Based on a Multiplicative Noise Model[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28（4）： 647-653.
[8]	Xu P L, Shimada S. Least Squares Parameter Estimation in Multiplicative Noise Models[J]. Communications in Statistics⁃Simulation and Computation, 2000, 29（1）： 83-96.
[9]	师芸. 乘性随机误差模型的最小二乘平差与精度评定[J]. 西南交通大学学报, 2014, 49（5）： 799-803. Shi Yun. Least Squares Adjustment and Accuracy Estimation in Multiplicative Error Models[J]. Journal of Southwest Jiaotong University, 2014, 49（5）： 799-803.
[10]	王乐洋, 陈涛, 邹传义. 病态乘性误差模型的加权最小二乘正则化迭代解法及精度评定[J]. 测绘学报, 2021, 50（5）： 589-599. Wang Leyang, Chen Tao, Zou Chuanyi. Weighted Least Squares Regularization Iteration Solution and Precision Estimation for Ill-Posed Multiplicative Error Model[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50（5）： 589-599.
[11]	Xu P L, Shi Y, Peng J H, et al. Adjustment of Geodetic Measurements with Mixed Multiplicative and Additive Random Errors[J]. Journal of Geodesy, 2013, 87（7）： 629-643.
[12]	师芸. 加乘性混合误差模型参数估计方法及其应用[J]. 武汉大学学报（信息科学版）, 2014, 39（9）： 1033-1037. Shi Yun. Least Squares Parameter Estimation in Additive/Multiplicative Error Models for Use in Geodesy[J]. Geomatics and Information Science of Wuhan University, 2014, 39（9）： 1033-1037.
[13]	Wang L Y, Chen T. Virtual Observation Iteration Solution and A-Optimal Design Method for Ill-Posed Mixed Additive and Multiplicative Random Error Model in Geodetic Measurement[J]. Journal of Surveying Engineering, 2021, 147（4）： 04021016.
[14]	Shi Y, Xu P L. Adjustment of Measurements with Multiplicative Random Errors and Trends[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18（11）： 1916-1920.
[15]	朱建军, 谢建, 陈宇波, 等. 附不等式约束平差的理论与方法研究[J]. 测绘工程, 2008, 17（6）： 1-5. Zhu Jianjun, Xie Jian, Chen Yubo, et al. Research on Theory and Methods of Inequality Constrained Least Squares[J]. Engineering of Surveying and Mapping, 2008, 17（6）： 1-5.
[16]	Judge G G, Takayama T. Inequality Restrictions in Regression Analysis[J]. Journal of the American Statistical Association, 1966, 61（313）： 166-181.
[17]	谢雪梅, 宋迎春, 肖兆兵. 附不等式约束平差模型的一种快速搜索算法[J]. 武汉大学学报（信息科学版）, 2018, 43（9）： 1349-1354. Xie Xuemei, Song Yingchun, Xiao Zhaobing. A Fast Search Algorithm in Adjustment Model with Inequality Constraint[J]. Geomatics and Information Science of Wuhan University, 2018, 43（9）： 1349-1354.
[18]	Remondi B W. Real-Time Centimeter-Accuracy GPS： Initializing While in Motion （Warm Start Versus Cold START）[J]. Navigation, 1993, 40（2）： 199-208.
[19]	Liu X L, Zhou M. A One-Layer Recurrent Neural Network for Non-smooth Convex Optimization Subject to Linear Inequality Constraints[J]. Chaos, Solitons & Fractals, 2016, 87： 39-46.
[20]	王乐洋, 李海燕, 陈晓勇. 拟牛顿修正法解算不等式约束加权总体最小二乘问题[J]. 武汉大学学报（信息科学版）, 2018, 43（1）： 127-132. Wang Leyang, Li Haiyan, Chen Xiaoyong. A Quasi Newtonian Correction Algorithm for Weighted Total Least Squares Problem with Inequality Constraints[J]. Geomatics and Information Science of Wuhan University, 2018, 43（1）： 127-132.
[21]	谢建, 龙四春, 李黎, 等. 不等式约束加权整体最小二乘的凝聚函数法[J]. 武汉大学学报（信息科学版）, 2018, 43（10）： 1526-1530. Xie Jian, Long Sichun, Li Li, et al. An Aggregate Function Method for Weighted Total Least Squares with Inequality Constraints[J]. Geomatics and Information Science of Wuhan University, 2018, 43（10）： 1526-1530.
[22]	朱建军, 谢建. 附不等式约束平差的一种简单迭代算法[J]. 测绘学报, 2011, 40（2）： 209-212. Zhu Jianjun, Xie Jian. A Simple Iterative Algorithm for Inequality Constrained Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40（2）： 209-212.
[23]	王乐洋, 邹传义. 乘性误差模型参数估计及精度评定的Sterling插值方法[J]. 武汉大学学报（信息科学版）, 2022, 47（2）： 219-225. Wang Leyang, Zou Chuanyi. Sterling Interpolation Method for Parameter Estimation and Precision Estimation in Multiplicative Error Model[J]. Geomatics and Information Science of Wuhan University, 2022, 47（2）： 219-225.

施引文献

资源附件(0)

图(6) / 表(3)

计量

文章访问数: 891
HTML全文浏览量: 107
PDF下载量: 54
被引次数: 0

不等式约束下加乘性混合误差模型的简单迭代解法

作者简介: 王乐洋,博士,教授,研究方向为大地测量反演及大地测量数据处理。wleyang@163.com

计量

出版历程

A Simple Iterative Solution for Mixed Additive and Multiplicative Random Error Model with Inequality Constraints

计量

出版历程

目录

作者简介:
王乐洋,博士,教授,研究方向为大地测量反演及大地测量数据处理。wleyang@163.com