Voronoi图是对空间的一种无缝分割方法，可以用于描述空间邻近关系^[1-2]、最近邻操作^[3]、空间影响范围，也可用于空间内插分析、设施选址分析^[4]、居民点布局、物流配送、空间认知和空间数据综合等^[5-6]，在空间实体匹配过程中具有易于建立空间实体的空间对应关系^[7-8]、有效减少匹配候选集搜索空间以及减少误配实体等优势。但前期研究发现，Voronoi图的边界位置精度在一定程度上会影响匹配结果，为了提升利用Voronoi图进行多尺度面状居民地匹配的质量和效率，迫切需要设计出易于实现、性能好、精度高、实用的面实体的Voronoi图算法。

目前，有关构造Voronoi图算法的研究很多，就Voronoi图的生成特点而言，分为矢量法^[9-13]和栅格法^[14-16]。其中，矢量法主要分为两类：（1）直接法，即直接由点集生成Voronoi图，比如半平面法、增量构造法、分治法、平面扫描线法等^[10]；（2）间接法，利用Voronoi图与Delaunay三角网（Delaunay triangulation，DT）的对偶性，先根据点集生成DT，然后构建Voronoi图^[9，11]。现有算法对于构建平面点集的Voronoi图十分有效^[12]，但是难以直接用于构造面状居民地的Voronoi图。王新生等^[17]提出了基于ArcGIS软件构建任意发生元的Voronoi图的矢量逼近方法，利用有限点来逼近原始图形发生元，从而代替原始图形，构建离散点集的普通Voronoi图，消除多余的Voronoi边和多余Voronoi顶点，得到原始发生元的逼近Voronoi图。该算法思路较好，但自动化程度低。张辉等^[10]针对地理信息系统（geographic information system，GIS）中线状、面状等复杂形态地理要素，提出一种构建任意发生元Voronoi图的实用算法，主要思想也是发生元离散化以及Voronoi多边形合并，该算法需要事先去除发生元自身面状区域，过程相对复杂。然而，上述方法未讨论顶点的离散间隔距离设置方法及其对Voronoi图应用的影响。李佳田等^[13]也利用发生元离散化的思路，融合了最近特征点，且将部分生长元进行迭代离散计算，但这种算法将生长元结点最小距离作为离散间距，未考虑边界位置精度与离散点数量之间的平衡问题，在面对复杂面状实体时，消耗的时间和内存空间较多，可靠性差。文献[9，11]利用相邻居民地多边形中相互通视的顶点构建DT，需要大量的空间关系计算，且未提供详细的通视点计算方法和整体三角网构建策略。

鉴于现有居民地Voronoi图算法的不足，本文在已有研究的基础上，提出了一种面向多尺度面状居民地匹配的Voronoi图自适应构建算法（adaptive Voronoi diagrams algorithm for matching multi-scale areal residential areas，AVARA）。该算法综合考虑了Voronoi图边界位置精度与算法的时间性能，有利于提升多尺度面状居民地的匹配质量。

1 AVARA

AVARA基于发生元离散化思想，并借鉴地理学第一定律的基本思想，即越相近的事物之间越相关，依据较邻近的邻居对要素插入的点相对密一些、相离较远的邻居对要素插入的点相对稀疏或不插入点的原则进行算法实现。

1.1   算法流程

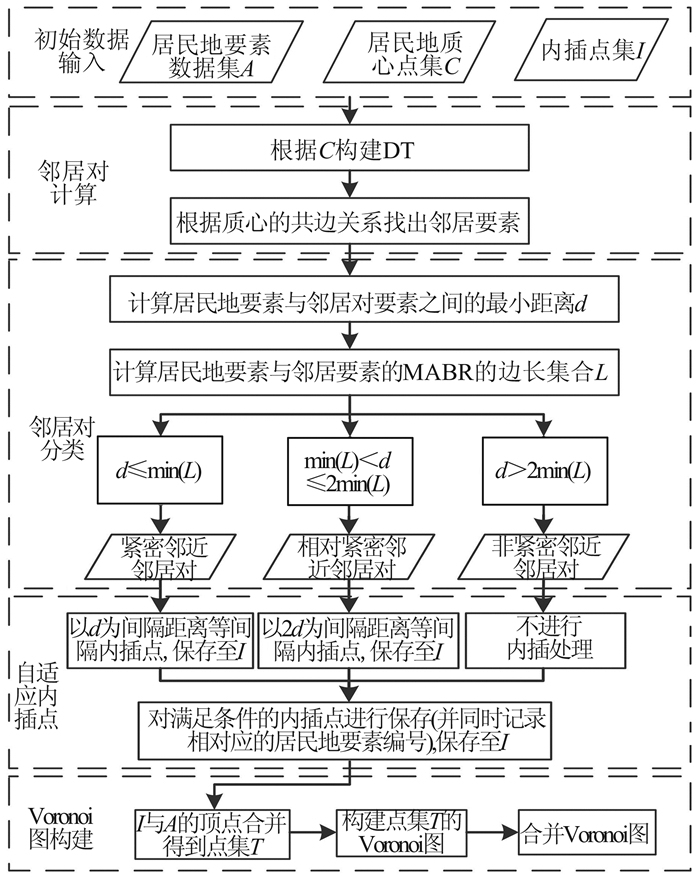
AVARA构建面状居民地的Voronoi图的流程见图 1，主要包括以下5个步骤：（1）初始数据输入，主要是输入居民地要素数据集A、居民地多边形质心点集C以及自适应内插点集I；（2）邻居对计算，邻居对指某居民地要素与其邻近的某居民地要素构成的集合，利用居民地质心点集C构建DT，再利用DT获取当前居民地要素的所有邻居要素，构建邻居对；（3）邻居对分类，利用居民地要素与其邻居对要素之间的最小距离d与两个要素的最小面积外包矩形（minimum area bounding rectangle，MABR）的边长最小值的大小关系，将邻居对分为紧密邻近邻居对（close neighbor pair，CP）、相对紧密邻近邻居对（relatively close neighbor pair，RP）、非紧密邻近邻居对（not close neighbor pair，NP）3类；（4）自适应内插点，针对不同类型的邻居对采取不同的边界点生成策略；（5）Voronoi图构建，利用自适应生成的边界点和居民地原始顶点构建点要素的Voronoi图，将具有相同居民地要素编号的Voronoi多边形合并，即可生成居民地的Voronoi图。

图  1  AVARA流程图

Figure  1.  Flowchart of AVARA

下载: 全尺寸图片 幻灯片

1.2   空间邻居对的计算

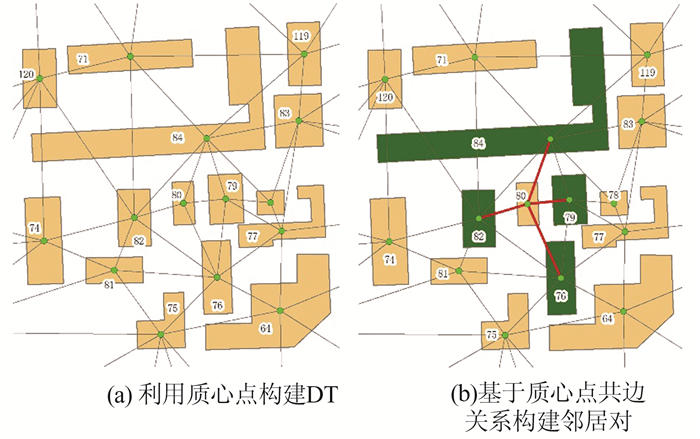
DT已经被证明是空间聚类中捕获拓扑邻接的有力工具^[18-19]，因此，本文使用居民地多边形质心点集C的DT来计算居民地的邻居要素，从而构建邻居对。邻居要素的计算过程如图 2所示。首先提取居民地要素的质心点，即图 2（a）中的绿色点，得到质心点集C={p_i|i=1，2…n}，表示某居民地多边形的质心点；然后利用C来构建DT；最后利用质心点连接相同的三角形边的关系，得到当前居民地要素的邻居对集合P_i={（A_i，A_j）|i≠j，i，j=1，2…n}，其中，A_i表示要素编号为i的居民地要素，A_j表示A_i的邻居居民地要素。如图 2（b）所示，要素编号为80的居民地要素的邻居对集合为P₈₀={（80，76），（80，79），（80，84），（80，82）}。

图  2  面状居民地的邻居对计算

Figure  2.  Calculation of Neighbor Pairs of Areal Residential Areas

下载: 全尺寸图片 幻灯片

1.3   空间邻居对的分类

在计算出每个居民地要素的邻居对之后，需要根据邻居要素间的距离对邻居对进行分类，以便根据不同策略进行边界点的内插。空间邻近性是人们空间认知的结果，在空间领域通常被认为是一种位置或距离关系。地图综合领域的学者认为，当两个要素的基高比（即面要素的面积与面要素最长骨架线的长度之比，是对面要素的平均宽度的描述）之和大于或等于狭长桥接面的间距时，两个面要素适合毗邻化；反之，当桥接面的间距大于两个要素的基高比之和时，不适合毗邻化，即两个要素不适合作为毗邻化处理的邻居。借鉴该思想，AVARA根据当前居民地要素与其邻居要素之间的最小距离d（两个居民地要素边界点之间的最短欧氏距离，当两个要素相交时d=0）与这两个要素MABR的边长最小值的大小关系进行分类，考虑到居民地边界离散化时应该尽可能少地生成离散点，AVARA进行了更严格的邻近条件约束，具体判定方法如下：

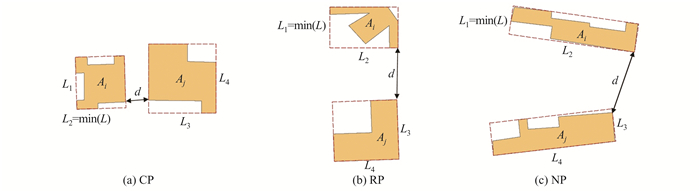
1）CP。要求邻居对要素之间的最小距离不大于MABR的边长最小值，即$d\le \mathrm{m}\mathrm{i}\mathrm{n}\left(L\right)$，其中，L为两个要素MABR的边长集合，L={L₁，L₂…L₈}；min（）为最小值函数。CP的示例见图 3（a）。

图  3  邻居对分类

Figure  3.  Classification of Neighbor Pairs

下载: 全尺寸图片 幻灯片

2）RP。要求邻居对要素之间的最小距离不大于2倍的MABR的边长最小值（理想状态下，两个邻居对要素的基高比相等，此时2倍的MABR的边长最小值等于两个邻居对要素的基高比之和），且大于MABR的边长最小值，即$\mathrm{m}\mathrm{i}\mathrm{n}\left(L\right)<d\le \mathrm{2}\mathrm{m}\mathrm{i}\mathrm{n}\left(L\right)$。RP的示例见图 3（b）。

3）NP。要求邻居对要素之间的最小距离大于2倍的MABR的边长最小值，即$d>\mathrm{2}\mathrm{m}\mathrm{i}\mathrm{n}\left(L\right)$。NP的示例见图 3（c）。

1.4   基于邻居对类别的边界点自适应生成

基于Voronoi图的多尺度面状居民地匹配中，需要利用Voronoi多边形去查询候选匹配要素，其边界位置精度会对查询结果产生一定的影响，通常对匹配数据集中位置邻近的居民地要素的匹配影响较大（这种情况就要求Voronoi边界位置精度尽可能高），而对相离较远的居民地要素的匹配影响较小或不影响。因此，AVARA对不同类型的邻居对要素采取不同的距离间隔在居民地边界上内插点，遵循较邻近的邻居对要素插入的点相对密一些，相离较远的邻居对要素插入的点相对稀疏或不插入点的原则，从而平衡边界位置精度与离散点数量之间的关系。

假定面状居民地要素数据集A={A₁，A₂…A_n}，A_i（i=1，2…n）表示A中的某一居民地要素，Q_i={q_i0，q_i1…q_im}为A_i的原始顶点集合。若在A_i的边界线上等距离间隔内插出k个顶点，理论上k越大，生成的Voronoi图边界越逼近理论值，但是消耗的时间和内存空间也越多。在数据集A间隔距离已知的情况下，k的计算式为：

式中，int[]为取整函数；L（A_i）表示A_i的周长；λ表示间隔距离。

AVARA对不同类型邻居对的λ取值策略如下：（1）CP。取邻居对要素之间的最小距离作为在居民地要素边界线段上生成边界点的间隔距离，即λ=d。（2）RP。取2倍的邻居对要素之间的最小距离作为在居民地要素边界线段上生成边界点的间隔距离，即λ=2d。（3）NP。除居民地要素边界顶点外，不需要在居民地边界线上生成点。

生成居民地原始顶点以及自适应内插出每个顶点时，记录该点所在居民地多边形A_i的要素编号，设A_i上内插点的集合为I_i，则A中所有内插点和多边形顶点的集合T为Q_i和I_i的合集。

1.5   Voronoi图构建方法

AVARA首先利用三角网生长算法对点集T构建Voronoi图，然后将具有相同居民地要素编号的Voronoi多边形合并，即可生成面状居民地的Voronoi图，Voronoi图构建过程如图 4所示。图 4（a）中的绿色点为居民地顶点和居民地边界上的内插点，其并集即为点集T，图 4（b）中黑色多边形为基于点集T构建的Voronoi图，图 4（c）中红色多边形为基于居民地要素编号相同的条件将图 4（b）中黑色多边形合并成的Voronoi图。

图  4  面状居民地的Voronoi图构建过程

Figure  4.  Process of Creating Voronoi Diagrams of Areal Residential Areas

下载: 全尺寸图片 幻灯片

1.6   Voronoi图位置精度评价方法

根据Voronoi区域内的任意一点距当前发生元的距离比距平面中的其他发生元都近的原则，比较不同算法得出的Voronoi图的几何精度，即理论上的Voronoi多边形应满足：

式中，V_i表示当前居民地要素A_i的Voronoi多边形；p为欧几里得平面上的任意一点；d_s为任意点与居民地要素之间的最短欧氏距离。

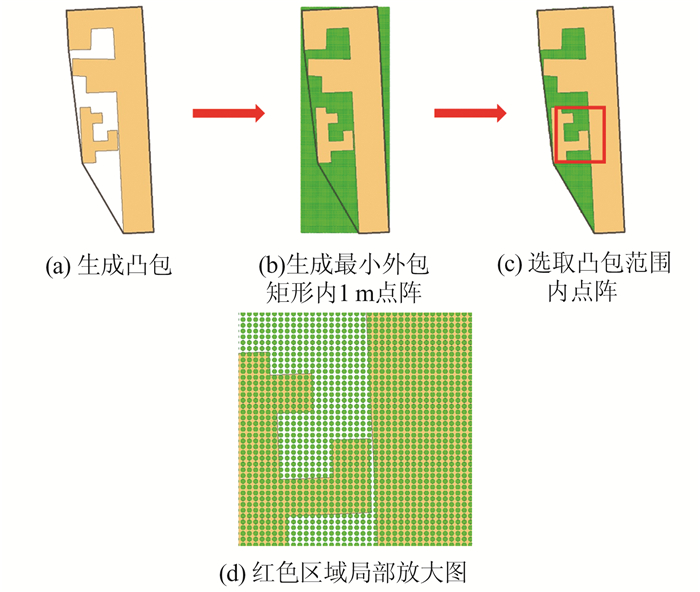
本文设计了如下方案检验紧密邻近邻居对之间的Voronoi多边形的边界精度：选取多对CP，针对一对CP，首先计算出CP的凸包；然后构建以CP的最小外包矩形为边界的等间隔距离的点阵（间隔距离依据数据集的制图精度确定），通常点阵越密集，越能体现出精度差距；最后通过空间关系查询获取CP的凸包范围内的点用于Voronoi多边形的边界精度检验。具体方法为：（1）遍历落在凸包范围中的点，计算该点到其对应Voronoi多边形所对应的居民地要素的最短距离d_si以及该点到其他居民地多边形的最短距离d_sj，如果d_si≤d_sj，则该点为符合要求的正确点，否则为错误点；（2）以正确点数或错误点数的统计值来评价Voronoi多边形的边界精度，正确点数越多，说明算法的边界精度越高。

2 实验与分析

为检验算法的有效性和实用性，本文进行了相关实验与算法对比分析，AVARA通过Microsoft Visual Studio2010（C#）+ArcGIS Engine 10.2实现，计算机基本配置为Intel Core（TM）i5-6200U CPU，内存为8 GB。

2.1   构建Voronoi图的实验数据

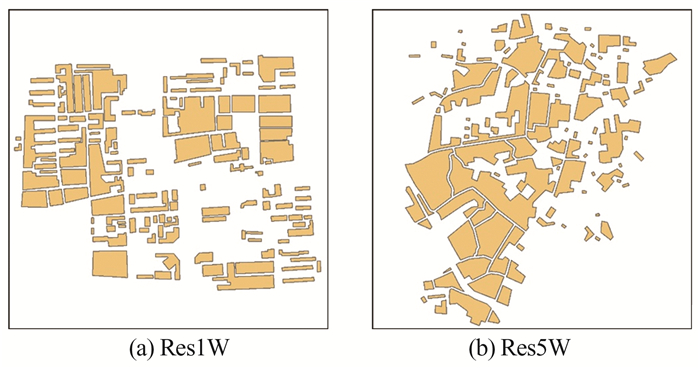
为了检验AVARA构建面状居民地Voronoi图的效果，本文选取不同地图比例尺的矢量面状居民地数据集进行实验，包括北京市昌平区某区域的面状居民地数据集（地图比例尺为1∶10 000，地理范围约0.22 km²，包含129个居民地要素），以及金华市兰溪区某区域的面状居民地数据集（地图比例尺为1∶50 000，地理范围约1.8 km²，包含108个居民地要素），将它们分别命名为Res1W、Res5W，实验数据如图 5所示。

图  5  构建Voronoi图的实验数据

Figure  5.  Experimental Data for Creating Voronoi Diagrams

下载: 全尺寸图片 幻灯片

2.2   实验与结果

采用AVARA、通视点算法^[9，11]和等间隔算法^[10，13]，利用Res1W和Res5W实验数据进行Voronoi图构建实验并进行对比分析。等间隔法的间隔距离λ计算式为：

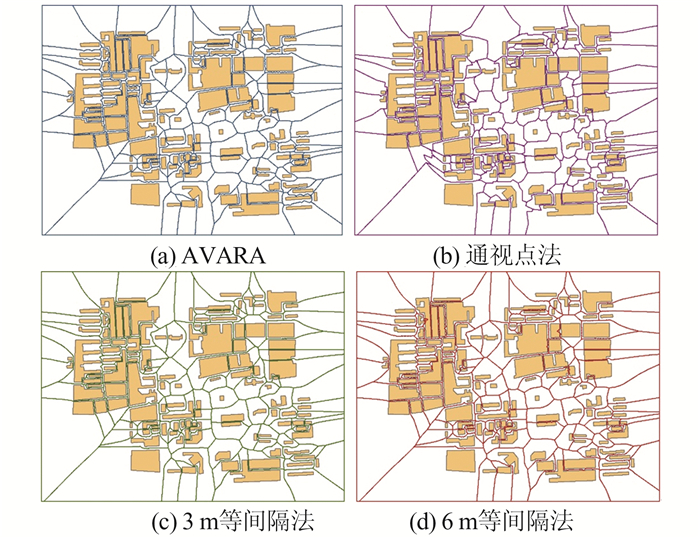
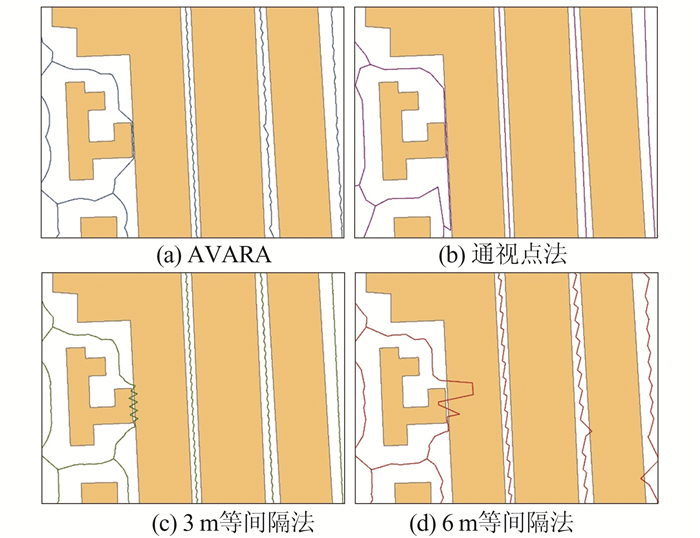
式中，D（A）为面状居民地要素数据集A的比例尺分母值，D（A）/1 000表示图纸上1 mm对应的实地长度；1/10表示图纸上1 mm距离人眼能识别的比例；$\mu$（1≤$\mu$≤10）表示距离容差系数，考虑到数据偶然误差一般不超过3倍中误差，这里取$\mu$=3，另外考虑到数据制图综合等引起的质量问题，本文将容许的误差再扩大一倍，即取$\mu$=6，实验时取$\mu =\mathrm{3}$、$\mu =\mathrm{6}$两种情况进行比较，即Res1W实验数据的等间隔距离为3 m和6 m，Res5W实验数据的等间隔距离为15 m和30 m。

不同算法对Res1W的Voronoi图计算结果如图 6所示，图 7是图 6的局部放大效果。由图 7可以看出，AVARA与通视点法生成的Voronoi图存在较大差异，而3 m等间隔法与6 m等间隔法生成的Voronoi图边界线存在锯齿且与居民地相交。

图  6  不同算法对Res1W的Voronoi图计算结果

Figure  6.  Voronoi Diagrams of Res1W Created by Different Algorithms

下载: 全尺寸图片 幻灯片

图  7  不同算法对Res1W的Voronoi图局部结果

Figure  7.  Local Results of Voronoi Diagrams of Res1W Created by Different Algorithms

下载: 全尺寸图片 幻灯片

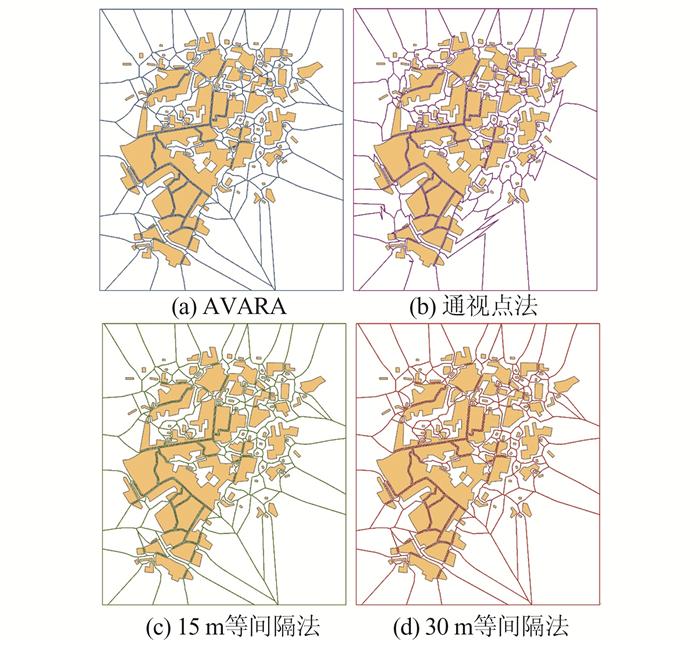
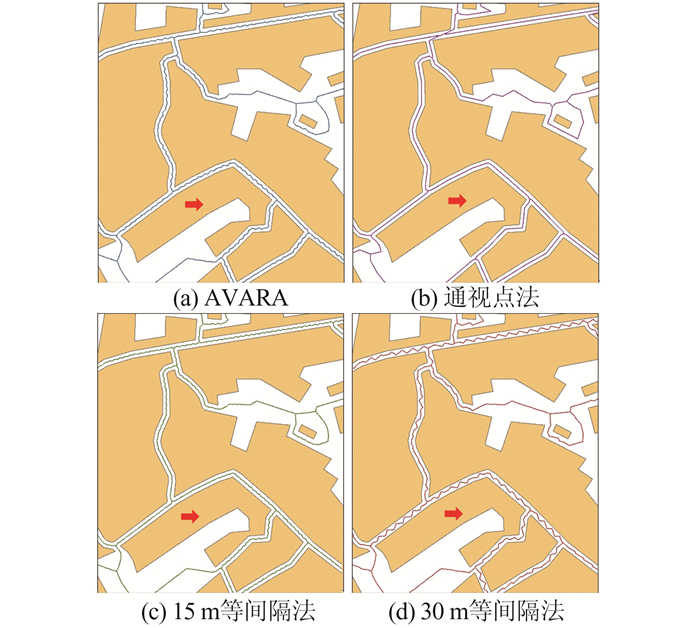
不同算法对Res5W的Voronoi图计算结果如图 8所示，图 9是图 8的局部放大效果。由图 9可以看出，4种算法生成的Voronoi图总体相似，但也存在局部的差异，如红色箭头所指的要素的Voronoi图边界线，通视点法与其他3种方法生成的结果差异明显，30 m等间隔法生成的Voronoi图边界线锯齿比较明显。

图  8  不同算法对Res5W的Voronoi图计算结果

Figure  8.  Voronoi Diagrams of Res5W Created by Different Algorithms

下载: 全尺寸图片 幻灯片

图  9  不同算法对Res5W的Voronoi图局部结果

Figure  9.  Local Results of Voronoi Diagrams of Res5WCreated by Different Algorithms

下载: 全尺寸图片 幻灯片

2.3   结果比较分析

2.3.1   位置精度比较

本文从Res1W和Res5W数据中各挑选出比较有代表性的3对邻居对，检验Voronoi多边形的边界精度。Res1W中不同算法生成的3个局部区域的Voronoi图见表 1。以局部区域1为例，其生成用于位置精度检测的间隔距离为1 m的点阵的过程见图10，种方法生成的Voronoi图边界位置精度评价结果见表 2。

表  1  Res1W中3个局部区域的Voronoi图

Table  1.  Voronoi Diagrams of Three Local Regions in Res1W

算法	局部区域1	局部区域2	局部区域3
AVARA
通视点法
3 m等间隔法
6 m等间隔法

下载: 导出CSV 

| 显示表格

图  10  Voronoi多边形位置精度检测点阵

Figure  10.  Points for Detecting Location Precision of Voronoi Polygons

下载: 全尺寸图片 幻灯片

表  2  Res1W中3个局部区域的Voronoi图质量比较

Table  2.  Quality Comparison of Voronoi Diagrams of Three Local Regions in Res1W

算法	局部区域1			局部区域2			局部区域3			合计
	正确数	错误数		正确数	错误数		正确数	错误数		正确数	错误数
AVARA	5 329	0		2 749	9		9 270	4		17 348	13
通视点法	5 164	165		2 743	15		9 245	29		17 152	209
3 m等间隔法	5 318	11		2 757	1		9 254	20		17 329	32
6 m等间隔法	5 253	76		2 729	29		9 221	53		17 203	158

下载: 导出CSV 

| 显示表格

Res5W中不同算法生成的3个局部区域的Voronoi图见表 3。精度检验方法与Res1W一致，检验点阵的间隔距离为5 m。4种不同方法生成的Voronoi图边界位置精度评价结果见表 4。

表  3  Res5W中3个局部区域的Voronoi图

Table  3.  Voronoi Diagrams of Three Local Regions in Res5W

算法	局部区域1	局部区域2	局部区域3
AVARA
通视点法
15 m等间隔法
30 m等间隔法

下载: 导出CSV 

| 显示表格

表  4  Res5W中3个局部区域的Voronoi图质量比较

Table  4.  Quality Comparison of Voronoi Diagrams of Three Local Regions in Res5W

算法	局部区域1			局部区域2			局部区域3			合计
	正确数	错误数		正确数	错误数		正确数	错误数		正确数	错误数
AVARA	4 440	13		2 459	9		4 201	5		11 100	27
通视点法	4 448	5		2 447	21		4 203	3		11 098	29
15 m等间隔法	4 445	8		2 466	2		4 205	1		11 116	11
30 m等间隔法	4 419	34		2 454	14		4 193	13		11 066	61

下载: 导出CSV 

| 显示表格

由表 2可以看出，AVARA在Res1W中构建的Voronoi图的质量最高。由表 4可以看出，AVARA在Res5W中构建的Voronoi图的质量较好，仅次于15 m等间隔法。

2.3.2   时间性能比较

不同方法对Res1W、Res5W数据生成Voronoi图的耗时结果见表 5。从表 5可以看出，通视点算法耗时远多于其他3种算法，主要原因是通视点计算及局部三角网构建时的空间关系判断较为耗时，算法过程也相对复杂，涉及到通视点计算、构建三角网、骨架线提取、线转面等步骤。AVARA能够自适应地构建满足多尺度面状居民地匹配要求的Voronoi图，其在局部位置精度与时间性能方面均优于通视点法、Res1W数据的3 m及6 m等间隔内插点法；在Res5W数据中，AVARA与30 m等间隔法相比，所耗时间多6 s，但AVARA的局部位置精度显著提高，而后者边界出现了很多较大的锯齿现象（见表 3），与15 m等间隔内插点法相比，AVARA的位置精度稍微偏低，几乎不会影响匹配结果，但所耗时间少10 s，即时间性能提升了40%。

表  5  Res1W与Res5W中不同算法构建Voronoi图的耗时比较

Table  5.  Computation Time Comparison of Voronoi Diagrams of Res1W and Res5W

数据	算法	（1）			（2）			（3）			（4）		耗时合计/s
		步骤	耗时/s		步骤	耗时/s		步骤	耗时/s		步骤	耗时/s
Res1W	AVARA	创建顶点和边界内插点	23（7 596个点）		创建Voronoi图	23		合并Voronoi图	4		—	—	50
	3 m等间隔法		25（13 819个点）			42			6			—	73
	6 m等间隔法		15（8 343个点）			33			5			—	53
	通视点法	创建顶点	5		创建三角网	467		计算Voronoi边界线	119		Voronoi边界线转面	1	592
Res5W	AVARA	创建顶点和边界内插点	12（3 960个点）		创建Voronoi图	10		合并Voronoi图	3		—	—	25
	15 m等间隔法		14（5 685个点）			16			5			—	35
	30 m等间隔法		8（3 780个点）			9			3			—	20
	通视点法	创建顶点	3		创建三角网	378		计算Voronoi边界线	119		Voronoi边界线转面	1	501

下载: 导出CSV 

| 显示表格

3 结语

本文提出了一种面向多尺度面状居民地匹配的Voronoi图自适应构建算法——AVARA，提出了基于空间邻居要素大小、距离及邻居对分类策略的居民地边界内插点方法，避免了内插点的冗余，设计了Voronoi多边形位置精度评价方法。实验结果表明，AVARA整体优势明显，在满足多尺度面状居民地匹配要求的Voronoi多边形位置精度的同时，保持了较好的时间性能，缓解了计算效率与边界位置精度及离散点数量的平衡问题，而且AVARA可以自适应地计算出内插点的间隔距离，不需要人工依据地图比例尺等信息设定距离参数，因此相比其他方法更具有普适性与实用性。

然而，AVARA算法仍需进一步改进，如目前内插的点数可能依然存在冗余，因为实体匹配时主要需要提高邻近边界上的内插点数，而其他位置不一定需要插入很多点。另外，AVARA目前还不能满足存在拓扑邻接的居民地的数据集的Voronoi图生成。