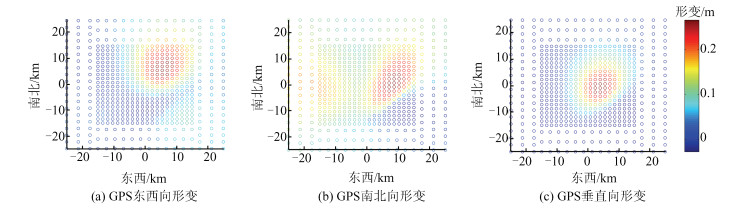
A Two-Step Solution Method for the Co-seismic Slip Distribution Inversion of Earthquake Faults in Geodesy
-
摘要: 针对同震滑动分布反演中系数矩阵出现病态的问题,提出两步解法,并在两步解法反演过程中引入拉普拉斯二阶平滑矩阵进行平滑约束。该方法不仅改善了系数矩阵的病态问题,同时也很好地抑制了相邻断层面间出现大的梯度变化。在两步解法反演过程中,用L曲线法确定正则化参数。系统模拟实验表明,对于最大滑动量,该方法的反演结果较一步最小二乘法的反演结果精度提高了3.34%~19%;对于均方根误差,该方法的反演结果较一步最小二乘法减小了3.3%~13.3%。芦山地震反演结果表明,利用两步解法进行滑动分布反演是可行的。Abstract: As for the ill-posed coefficient matrix in the process of co-seismic slip distribution inversion, a two-step solution method is proposed, and the Laplace second-order smoothing matrix is used for smoothing constraint in this paper. This method not only solves the ill-posed problem of the coefficient matrix, but also suppresses the large gradient variation between adjacent fault patches. During the inversion process of two-step solution method, the L curve method is used to determine the regularization parameters. In this paper, systematic simulation experiments are carried out and the Lushan earthquake is used as an actual earthquake case. The maximum slip inversion results of simulation experiments show that the inversion result of two-step solution method has been improved between 3.34% and 19% than that of one-step solution method in accuracy. The root mean square error inversion result of two-step method is less between 3.3% and 13.3% than that of one-step solution method. The inversion results of the Lushan earthquake show that it is feasible to use the two-step solution for slip distribution inversion.
-
地球重力场是反映物质迁移的基本物理场,直接反映地球内部构造运动、地表质量迁移的本质和过程。地震、火山活动等地球动力学过程都会引起一定程度的地球重力场变化[1-7]。重力场对质量运动或变化信号敏感,适合定量研究各种地球系统过程的时空特性。高精度的地表重力场观测由于距离地壳内部场源近、观测位置固定重复、观测仪器精度高等特点,有利于发现与地壳内部场源直接相关的物理信号。
地震研究不仅依赖相关基础理论的发展,更依赖地震前后时空完整的高精度观测资料。流动重力观测获得的重力时变信号能较好地反映深部物质运移与地壳密度变化等构造活动信息,强震前区域重力场可能会观测到显著的重力异常变化特征,通过对重力时变信号的深入分析,能捕获到与孕震区物性变化有关的物理信息,利用高精度重力测量数据分析震前重力异常变化的时空分布特征,有助于判定未来大震的高风险区域,是利用重力手段开展地震预测的基本出发点。
1 流动重力监测网布局
1.1 重力网布局思路
流动重力监测网是进行地震重力测量的基础,是直接为地震预报服务的。地震监测预报业务能力的提升离不开高精度、高时空分辨率的重力场变化监测资料,而建设布局科学合理的台网是获取此类监测资料的前提。根据历史地震资料,地震学家在中国大陆划出了几十条地震带,涉及地域极广。在这些地震带上都布设密集的地震重力监测网是不切实际的,不仅自然条件和监测能力不允许,实际上也是不必要的。因此,按照地震工作的方针,只在有一定经济建设规模、人口比较稠密、社会影响显著的主要地震带布设相对密集的重力监测网,如南北地震带、天山地震带、华北地震带等。重力监测网的布设始终坚持服务于中强以上地震预测,尤其是强震/大震预测这一主题。
流动重力测量是对已经建立的重力点按观测程序进行联测,定期进行重复观测,形成重力场变化观测网络,并辅以绝对重力观测加以控制,获得高精度重力场的空间和时间变化。
1.2 重力网布局概况
地震重力监测网是全国地震前兆监测系统的一个重要组成部分和主要监测手段,主要用于精确监视区域重力场的动态演化,并用于地震孕育、发展、发生过程的追踪,为地震预报和相关的地球动力学研究服务。
中国大陆的流动重力测量工作始于1966年邢台地震后,1981年后得到长足发展。1981年前主要使用石英弹簧重力仪,测量精度在30~40 µGal,之后引进LaCoste-Romberg高精度重力仪,精度在10 µGal内。1990年前后,中国大陆的主要活动构造带或地震危险地区陆续建立了30多个区域重力监测网,形成了由近4 000个点组成的定期复测重力监测网,区域网各自独立,呈网状或条状,平均范围小于300 km×300 km[8-9]。1998年,中国地震局与原国家测绘局、原总参谋部测绘局和中国科学院等四部委共建了中国地壳运动观测网络工程(下简称网络工程),该工程建成了中国大陆统一的全国地震重力基本网[10-11]。
2008年汶川8.0级地震后,中国地震局高度重视流动重力监测与预报工作,认为各区域地震重力监测网覆盖区域较小,捕捉地震前兆的能力有限,大部分监测网虽然分布在中国大陆的一些主要活动构造带上,但强度不够、监测能力不足,如川滇地区的许多地震都发生在监测网外[8-9]。另外,各区域重力监测网彼此独立、自成体系,缺乏有效的联测和绝对重力基准控制,降低了观测资料的内在精度,不能得到区域重力场变化的绝对量,严重影响了观测资料的有效应用,使其不能在地震预报中发挥更大作用。因此,有必要将区域重力监测网连接成整体,建成统一重力观测基准,使地震重力监测网建设和观测技术得到快速发展[12-13]。在华北强震震情监视与跟踪、中国大陆地球物理场综合观测、中国大陆构造环境监测网络等重大项目资助下,对零散分布的地震重力监测网进行了多次整体结构优化改造,在重力网布局思路上不断创新,为中国大陆成场分布的地表重力场监测预报工作奠定了重要基础。2010年,由相对重力联测网和绝对重力控制网组成的中国大陆整体重力测量网[13]建成,每年定期开展观测。
21世纪以来,中国大陆发生了8次7级以上大震,包括2001年昆仑山口西8.1级、2008年汶川8.0级和于田7.3级、2010年玉树7.1级、2013年芦山7.0级、2014年于田7.3级、2017年九寨沟7.0级和2021年玛多7.4级地震,除了发生在青藏高原腹地的2001年昆仑山口西8.1级震中附近没有重力测点外,其他7次大震的震中附近均有一定的重力测点,尤其是2008年汶川8.0级、2013年芦山7.0级和2017年九寨沟7.0级地震,震中四周均有重力监测点,这为可靠地提取强震前的重力变化前兆信息打下了良好基础[9-11]。
2 重力数据处理
利用重力时变资料进行地震分析预测研究需要进行重力测量数据处理。只有通过必要的数据处理,从观测资料中提取可靠的重力变化信息,才能实现观测资料的价值。数据处理的目的是获得真实的重力测量值,描述重力场演变过程,从观测资料中获取反映地震孕育发生过程中的重力变化信息。重力观测资料的质量既依赖监测成果质量,也依赖处理资料方法,不同的资料处理方法可能会得到差异较大的结果,这在资料分析中尤为重要。
流动重力测量一般成网状布设,它包括基准点上的绝对重力测量以及联测点间的相对重力联测。相对重力联测具有机动灵活、省时省力、经济成本低等优点,能快速获取地震重点监视区的区域重力场变化。但相对重力联测获得的观测数据是相邻测点间的重力段差,需进行数据处理,又称平差。依据最小二乘原理进行平差,可以合理消除网中各种不符值,削弱偶然误差,消除系统误差,评定测量精度,同时获得流动重力测网中各点的重力值等。在平差之前需要进行预处理,包括对观测值进行固体潮、气压、一次项、仪器高改正等。
进行重力网平差,首先需要选择适当的平差基准,重力网平差基准的选择将直接影响重力场变化结果分析的可靠性[14]。重力网平差基准的选择可以有不同方式,包括经典平差、自由网平差和拟稳平差[15-16]。(1)当网内有2个以上绝对重力点时,一般采用经典平差,选取绝对重力点值作为平差的起算基准;(2)当网中无绝对重力控制、且多期测网测点或网型存在一定变化、但测网内存在部分稳定的重力测点时,通常采用拟稳平差;(3)当网中无绝对重力点、前后两期测网的测点和网型无大变化时,通常采用自由网平差。
1997年以前,中国地震局各施测单位独立的重力测网基本没有绝对重力点,地震重力的数据处理与分析工作由各单位对其测区进行,重力网数据处理无法满足经典平差方法的需求,因此,区域重力网的数据处理通常采用自由网平差与拟稳平差。1998—2009年,网络工程的重力网采用绝对重力控制的经典平差,其他区域网由于缺少绝对重力观测点仍采用自由网平差与拟稳平差。2010年以来,中国大陆流动重力监测网是由相对重力联测网和绝对重力控制网共同组成的,将中国大陆构造环境监测网络重力网与各施测单位的区域重力测网连接成整体,形成中国大陆流动重力统一观测网。因此,重力数据的处理从各省区地震重力网的独立计算,发展到相邻省区联合处理的整体平差计算,既扩大了研究区范围,又能有效提取各省区交界地带的重力场变化信息[17]。
综合利用地面绝对重力、相对重力资料的整体处理分析方法,获得测区内以绝对重力为基准的区域重力场变化。数据处理的重点是将绝对重力观测资料与同期的相对重力观测资料结合,其中绝对重力点构成高精度控制网,相对重力观测视为与该网的定期联测,形成具有绝对基准的区域动态监测网。具体数据处理步骤为:(1)使用中国地震局LGADJ软件对重力观测数据进行统一平差计算[18];(2)采用稳健估计法对少数存在误差较大的观测段差实行降权处理和粗差剔除,利用计算程序自动优化、合理确定各台仪器的先验方差后进行整体平差计算[19-20];(3)重力网平差采用弱基准,若基准点有误差、甚至异常,易从平差结果中发现,从而降低误差影响,且可通过平差使基准点重力值得到改善[19-20];(4)实测标定仪器的一次项[21],在野外作业中使用基线场的标定值,但随着测区的不同和观测时间的变化,重力仪的格值系数会发生变化,尤其是CG-5/6型重力仪格值系数会产生较大变化,应利用测网中的绝对重力点控制解算出区域适定解,精确标定仪器的格值系数,获取可靠重力变化[22];(5)采用贝叶斯方法提供的非线性零漂计算模型对仪器非线性漂移的漂移率变化进行估算,消除仪器零漂的影响[23];(6)用最小二乘配置等方法对重力观测数据进行拟合推估和滤波[9,11],以便突出显示构造因素的重力效应。
3 重力变化与构造运动及地震活动
根据流动重力监测情况和重力数据处理结果,可以获得不同时空尺度的区域重力场,作为分析研究重力场动态变化图像的依据,利用最小二乘配置、小波分析、双三次样条分析等方法,提取可靠重力场变化信息,系统分析研究多时空尺度的区域重力场动态变化图像演化特征与规律。
3.1 重力场时空演化特征
由于地壳介质的非均匀性和构造运动过程的复杂性,区域重力场的时空动态变化具有明显的不均匀性[11-13],主要表现为:
1)区域重力监测网范围不同,在不同时空尺度上的重力场动态变化图像存在明显差异。中国大陆整体重力网的观测资料能反映强震活动的主体区,高密度的地震重点监视区重力网的观测资料能反映出发震构造活动引起的局部重力异常。
2)不同时段的重力场在空间分布上表现出明显的差异性。在无显著变化时段,重力场空间分布比较零散,重力变化没有明显的规律性;在显著变化时段,区域重力场空间分布则表现出大范围的有序性变化和局部异常的相对集中性。
3)重力场变化与所处的地质构造环境等因素有关,沿块体构造活动带呈分区变化现象,一般表现为山区重力负值变化、盆地重力正值变化的继承性构造运动。
3.2 重力变化与构造活动的关系
地表重力场动态变化主要由地表观测点的位置变化、变形运动以及地球内部因构造块体变形运动的密度变化效应叠加引起,包含了丰富的构造运动信息[24-28]。
1)重力场变化能够较好地反映测区内主要构造断裂的构造运动过程。由于构造形变沿活动断裂带分布,当块体构造单元运动速率发生改变时,易在其边缘地区出现与地质构造线一致的重力变化梯度带,反映了块体构造单元的相对运动。
2)重力场变化与地壳深部活动断裂构造密切相关,区域重力场变化较显著的梯度带走向与深部构造活跃断裂带走向基本一致,构造单元的边缘往往容易出现重力等值线形态的转折和密集,形成重力变化高梯度带。
3)重力变化能较好地反映与地震孕育发生有关的断层构造活动,在震中区附近出现不同形态、不同规模的局部重力异常区及其伴生的重力变化梯度带。
总之,区域重力场动态变化与构造活动存在密切联系,重力资料能较好地反映在区域构造应力场和震源应力场作用下断层活动引起的重力效应。
3.3 地震孕育、发生过程的重力场变化特征
1966年邢台地震后,中国开始重力场时变的观测研究。20世纪70年代观测到1975年海城7.3级、1976年唐山7.8级等几次大震前重力变化,证实了震前重力异常的存在[1];20世纪90年代观测到1995年中缅交界7.3级地震前出现约110 µGal重力异常[28],1996年丽江7.0级地震前震中附近出现约120 µGal重力异常[8];近年来观测到2008年汶川8.0级和于田7.3级、2010年玉树7.1级、2013年芦山7.0级、2014年于田7.3级、2017年九寨沟7.0级和2021年玛多7.4级等大震前后重力变化[25-32]。
根据中国大陆不同时空尺度的区域重力场演化特征与规律[28-37],有学者提出以时空区域重力场作为分析重力场动态变化图像的依据,利用不同时空尺度的重力场变化,如相邻两期重力变化、年尺度重力变化、累积重力变化等,选取重力场变化趋势、重力异常形态、重力异常区的范围、持续时间、异常量级等作为判定指标,综合进行地震孕育发生的预测,具体见表 1。
表 1 重力异常与地震孕育发生的关系Table 1. Relation Between Gravity Anomaly and Earthquake Inoculation震级 潜在发震地点的重力场特征 趋势特征 异常范围/km 持续时间 异常量级/µGal 5 重力变化高梯度带 出现局部异常区 ≥100 0.5~1 a ≥50 6 与构造活动有关的重力变化高梯度带转弯部位,四象限分布特征中心附近 出现局部异常区 ≥200 1~3 a或更长 ≥80 7 与块体边界有关的重力变化高梯度带转弯部位,四象限分布特征中心附近 出现正、负局部异常区 ≥400 3~5 a或更长 ≥100 8 与一级块体边界有关的重力变化高梯度带转弯部位,四象限分布特征中心附近 出现正、负局部异常区 ≥600 5 a或更长 ≥120 由表 1可知,要了解地震孕育、发生过程的重力场变化特征,应从重力异常变化特征、空间范围、异常持续时间和异常量级4个因素来考虑。
1)强震发生之前,区域重力场出现大范围的有序性变化,震源区附近产生与地震孕育发生有关的局部重力异常区,并沿区域主要发震构造断裂带出现显著重力变化梯度带。由于孕震构造环境的差异,不同地震的重力变化响应具有明显差异。
2)强震易发生在与构造活动有关联的重力变化正、负异常区过渡的高梯度带上,重力变化等值线的拐弯部位或四象限中心附近。强震前震中区及其附近观测到明显的区域性重力异常及重力变化高梯度带,可能是地震孕育过程中观测到的重力前兆信息。
3)地震震级与重力异常变化的范围、持续时间和变化量级密切相关[17]。一般来讲,观测资料积累的时间越长越有利于判断强震发震震级,重力变化的空间分布特征与发震地点有关;震前重力异常变化覆盖范围越大,则震级越大;震前重力异常变化量级越大,则震级越大;震前2~3 a的观测对发震时间预测非常关键,6级以上地震相邻两期重力变化显著,2 a以上的累计重力变化更为显著,5级地震不存在这种现象。
大量研究成果表明[28-37],区域构造活动引起的重力时变异常是与地震孕育发生相关的前兆异常之一,特别是对于6级以上地震的孕震过程。
4 重力时变与强震预测
获取可靠的地震前兆信息是实现地震预测的前提。实践证明,通过对重力时变信号的深入分析,能捕获与孕震区物性变化有关的物理信息,是利用重力手段开展地震预测的基本出发点。
在地震预测实践方面,中国地震局于20世纪90年代就对滇西和河西地区利用流动重力观测资料进行了地震预测研究探索,观测到滇西地区1992年永胜5.1级和5.4级、1993年大姚5.3级地震前的重力场变化,1996年丽江7.0级地震前的重力异常变化,并对这几次地震曾进行了一定程度的预测[5,8]。1995年甘肃永登5.8级和2000年甘肃景泰5.9级地震前,河西地区也观测到明显的重力异常变化,并对这两次地震均进行了较准确的中期预测[38-39]。21世纪以来,李辉等[11]利用网络工程重力观测资料获得的1998年以来中国大陆2~3 a尺度重力场动态变化图像,较好地反映了中国大陆地壳构造运动和主要强震活动的基本轮廓。祝意青等[24]利用1998-2008年期间网络工程的重力观测数据,获得中国大陆地区以绝对重力为统一起算基准的重力场动态变化图像,认为中国大陆重力场变化与构造活动断裂和与强震孕育发展有着密切联系,强震易发生在沿构造活动断裂出现的重力变化正、负异常区过渡的高梯度带上以及重力变化等值线的拐弯部位。此外,祝意青等[25]还利用网络工程1998-2005年期间的重力资料对2008年汶川8.0级和于田7.3级等大震做出了准确的中期预测。
预测的主要依据:1998-2005年期间的累积重力变化表明,川滇菱形块体内部出现大范围的重力正值变化异常区,川滇菱形块体北部的四川地区出现较大范围的重力负值变化异常区,两异常区的升降差异变化超过100 µGal,并在马尔康-汶川-成都一带形成重力变化高梯度带(图 1)。
预测情况:发震时间:2007-2008年;发震地点:(103.7°E,31.6°N)为中心,半径200 km;震级:6~7级。
结果:2008年5月12日,汶川8.0级地震(103.4°E,31.0°N)发生在预测区内,预测震中位置距离汶川8.0级震中72 km,在北川与映秀两个极震区之间(图 2),时间、地点正确,震级提到7级。
预测依据:1998-2005年较长时期的网络重力变化表明,新疆与西藏交界地区出现了显著重力异常变化,最大变化差异量超过90 µGal,并在新疆于田-和田一带沿构造块体边界带形成显著的重力变化梯度带。
预测情况:发震时间:2007-2008年;发震地点:(80.0°E,36.0°N)为中心,半径200 km;震级:6~7级。
结果:2008年3月21日,于田7.3级地震(81.6°E,35.6°N)发生在预测区内,预测震中位置距离于田7.3级震中149 km,这在地震监测能力比较弱的地区是很准确的(新藏交界地区测点间距100~200 km,测点较稀)。
2008年汶川地震后,中国地震局重力学科管理部加强了重力监测预报研究工作,积极探索利用重力观测资料进行地震年度危险性预测,充分利用日益丰富的重力观测资料,在精细处理区域重力网观测资料的基础上,深入细致地研究区域重力场的动态演化特征与规律,从复杂多变的重力异常现象中寻找构造活动和地震前兆信息,开展震例回溯研究,跟踪分析区域性重力场的异常变化及其可能的中短期异常信息,提出了多种在强震前有预报意义的不同时空尺度的重力场变化特征模式[2,13,35-36]。在强震预测方法和判别指标的基础上,利用重力场动态变化资料对重点监视区的地震危险性进行年度预测和震后趋势判定,在全国地震重点危险区强震地点判定中发挥了重要作用,取得了一定程度的减灾实效[17,40-41],对近年来发生的2013年芦山7.0级和岷县6.6级、2014年鲁甸6.5级和于田7.3级、2016年门源6.4级、2017年九寨沟7.0级、2020年伽师6.4级、2021年漾濞6.4级和2022年门源6.9级地震等均进行了年度预测[29-35],尤其是强震发震地点的判定。表 2列出了近年来,利用重力观测资料对中国2013年以来10多次强震预测的情况。
表 2 2013年以来6级以上强震年度预测情况Table 2. Midterm Prediction Information of More than 6 Strong Earthquakes Since 2013预测震中 预测震级 预测时窗 发震地点 实际震级/级 实际震中 发震时间 102.2°E, 30.2°N 6级左右 2013年 四川芦山 7.0 103.0°E, 30.3°N 2013-04-20 105.2°E, 35.5°N 6~7级 2011—2013年 甘肃岷县 6.6 104.2°E, 34.5°N 2013-07-22 81.6°E, 35.6°N 7级左右 2014年 新疆于田 7.3 82.5°E, 36.1°N 2014-02-12 102.1°E, 28.8°N 7级左右 2014年 云南鲁甸
四川康定6.5
6.3103.3°E, 27.1°N
101.7°E, 30.3°N2014-08-03
2014-11-22102.2°E, 37.5°N 6级左右 2016年 青海门源 6.4 101.62°E, 37.68°N 2016-01-21 75.7°E, 39.3°N 6~7级 2016年 新疆阿克陶 6.7 74.04°E, 39.27°N 2016-11-25 85.5°E, 43.5°N 6级左右 2016年 新疆呼图壁 6.2 86.35°E, 43.83°N 2016-12-08 101.9°E, 34.7°N 6~7级 2016—2017年 四川九寨沟 7.0 103.82°E, 33.20°N 2017-08-08 75.8°E, 39.6°N 6~7级 2020年 新疆伽师 6.4 77.21°E, 39.83°N 2020-01-19 100.5°E, 25.8°N 6级左右 2020年 云南漾濞 6.4 99.87°E, 25.67°N 2021-05-21 101.2°E, 37.8°N 6级左右 2021—2022年 青海门源 6.9 101.26°E, 37.77°N 2022-01-08 由表 2可以看出,近年来利用流动重力资料对西部有监测能力地区发生的6级以上强震/大震均进行了较准确的中期预测,但也存在强震漏报的情况,如2017-11-18西藏米林6.9级、2020-07-23西藏尼玛6.6级等地震均发生在青藏高原重力监测能力较弱的地区,不能进行有效监控。
总的来说,流动重力观测资料能较好地反映出地震孕育发生过程中的重力异常变化,尤其是6级以上的强震。通过对流动重力观测资料及时进行缜密分析与研究,有可能对未来强震/大震做出较准确的中期预测,尤其是强震地点的判定。如2022年青海门源6.9级地震地点的预测(见表 2),地震发生在预测的祁连—海原断裂带冷龙岭段,预测的震中位置距离门源6.9级震中不到10 km,基本上一致。
5 问题与展望
获取可靠的地震前兆信息是实现地震预测的前提。重力变化测量是当前大地测量中最精密和困难的工作,地震监测获取的是微伽级变化。观测技术很重要,数据处理也十分关键,由于目前主要以绝对重力控制下的相对重力测量为主,因此,数据处理显得格外重要,应加强数据处理与分析,确保第一手资料的可靠性。此外,不同环境及物理因素导致的重力变化也要考虑,如环境变化、地下水、气压、冰后回弹等。
5.1 问题
在各种自然灾害中,地震是对人类生活影响最严重的自然灾害之一。通过地震监测预报能预测大震何时何地发生,对于造福人类来讲是非常重要的。地震监测的最终目的是为地震预报服务,虽然重力时变监测目前已在中国大陆的地震监测与研究中取得了较为成功的经验,但距离地震预测预防等减灾需求尚有不足,主要存在以下问题:
1)重力变化监测网布局分布不均匀。重力监测点主要分布于南北地震带与大华北地区,而在青藏高原及其周缘地区分布较少,时空分辨率不够,不足以实现对块体边界带的有效监测,所得到的重力变化监测信息是残缺不全的,对6级强震仍不完全具备监测能力,不能有效地捕捉到强震孕育发生过程中出现的完整前兆信息。
2)绝对重力控制程度较低。绝对重力与相对重力没有进行准同步测量,重力监测网缺少足够的绝对重力控制以及对相对重力测量仪器的格值系数精确标定。
3)地面重力与卫星重力缺少有效融合。卫星重力测量主要依托GRACE/GRACE-FO卫星观测资料,虽填补了青藏高原腹地无人区等观测空白,但未能与陆地重力测量形成有效融合,且囿于权限,只能获取国外机构提供的预处理结果,不能获取第一手原始观测资料。
4)新技术应用不足。重力观测仪器设备的核心传感器大都是20世纪研发的弹簧传感器,核心技术已逐渐落后,不能满足获取微小重力变化的需求。近年来,超导重力仪观测技术已发展成熟,但在现有地震重力监测台网中的装备很少,地震监测应用不足;量子重力仪发展快速,相关产品已具备较高的可用性,但目前尚未在地震重力监测中得到应用。
5)时变重力数据分析和研究中,构造和水的影响是造成地面重力变化最大的因素,一些地下水、地表变形、局部近地表水储量变化等干扰因素难以被精确剔除,如何扣除掉地下水等对重力变化的影响和贡献,有效提取反映构造和动力学变化的信号是亟待加强的工作。
5.2 展望
地震预报一直是世界公认的科学难题,地震机理极其复杂,但并不是完全不可知的。地震的发生本是地下构造运动由慢变快的变形过程,问题在于是否能观测、记录到,即使观测到了,又能否识别[42]。从科学技术上讲,实现有效的地震预测预报,首先需要对地震机理、地震孕育发生的物理过程有全面完整的认识;然后需要能够有效地监视地震孕育、发生过程,以便根据孕震过程的发震阶段进行地震预测。这两点一方面是科学理论,一方面是技术能力。近年来,中国地震局注重地震重力监测预报队伍建设与人才培养,一方面加强重力变化机理研究,另一方面对中国大陆地震重力观测网进行整体优化完善,加强地震监测能力建设,流动重力在地震预测预报中发挥着越来越重要的作用,虽取得了多次中期预测成功案例,但目前仍存在地震孕育发生过程中的重力变化机理认识不清、重力观测技术需进一步提高等问题。从长远发展来看,应加强以下工作:
1)发展高精度绝对重力观测技术代替流动相对重力观测技术;发展低漂移(超导)或无漂移式定点连续观测技术代替弹簧式定点连续观测技术;发展低空卫星重力观测技术弥补地面重力观测技术的不足[35]。
2)加强协作,发挥多部门优势,联合大学、科学院所开展中国大陆重力场时变及强震孕育发生机理研究,深化强震发生机理的认识。
3)在中国地震科学实验场的高风险区,建立高密度的绝对重力观测网络或具有良好绝对重力控制的相对重力观测网络,开展密集的强化监测,这有可能揭示高风险区震中附近的地下结构分布特征,提取强震/大震孕育过程中震源变化伴随的绝对重力变化信号,获取高精度绝对重力动态变化图像,为地震孕育环境和孕育过程监测提供前所未有的强大支持。
未来,随着观测技术的进步、重力场时空监测分辨力的增强,强震孕育发生过程中的重力变化机理研究的深入,时变重力观测将进一步提高其在地震分析预报中的能力,服务于中国防震减灾事业的发展需要。
-
表 1 模拟实验预设模型参数
Table 1 Default Model Parameters for Simulation Experiments
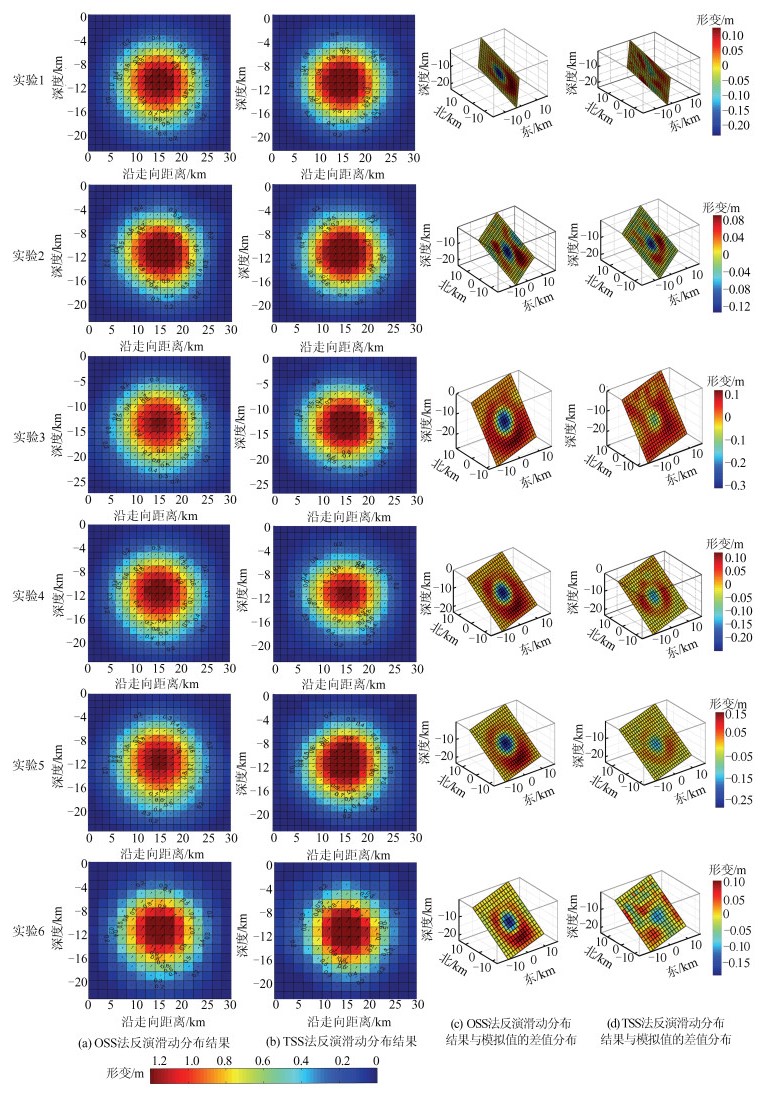
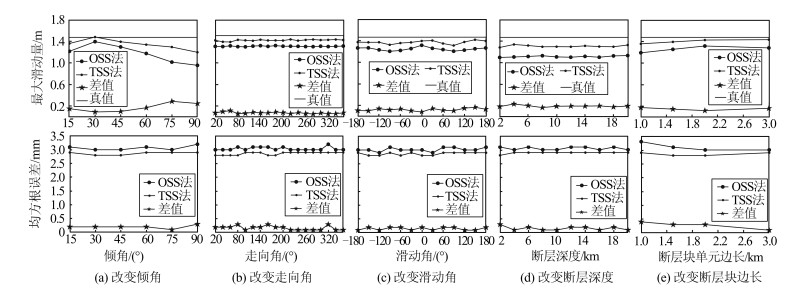
预设参数 实验1 实验2 实验3 实验4 实验5 实验6 断层块边长/km 1.5 1.5 1.5 1.5 1.5 2 最大滑动量/m 1.472 1.472 1.472 1.472 1.472 1.500 平均滑动量/m 0.3104 0.3104 0.3104 0.3104 0.3104 0.3105 滑动角/(°) 43 43 43 43 65 43 断层走向/(°) 70 55 70 70 70 70 断层倾向/(°) 50 50 65 50 50 50 震源深度/km 12.5 12.5 12.5 10.8 12.5 12.5 矩震级 Mw6.582 Mw6.582 Mw6.582 Mw6.582 Mw6.582 Mw6.583 表 2 模拟实验两种方法反演结果
Table 2 Inversion Results of Two Methods for Simulation Experiments
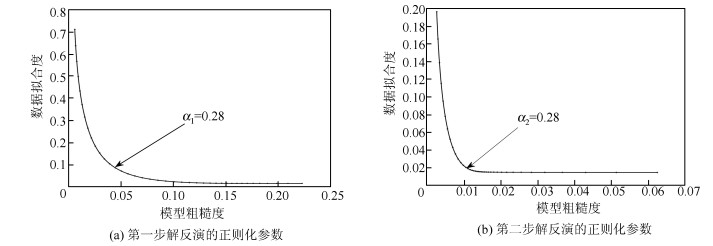
方法 参数 实验1 实验2 实验3 实验4 实验5 实验6 OSS法 最大滑动量/m 1.250 1.240 1.196 1.249 1.207 1.312 平均滑动量/m 0.318 0.321 0.322 0.320 0.324 0.318 矩震级 Mw6.589 Mw6.592 Mw6.593 Mw6.591 Mw6.594 Mw6.589 均方根误差/mm 3.0 3.1 3.1 3.1 3.0 3.0 平滑因子α1 0.28 0.3 0.18 0.27 0.29 0.25 TSS法 最大滑动量/m 1.388 1.334 1.373 1.378 1.371 1.423 平均滑动量/m 0.311 0.313 0.315 0.315 0.314 0.310 矩震级 Mw6.583 Mw6.585 Mw6.587 Mw6.586 Mw6.586 Mw6.582 均方根误差/mm 2.8 2.8 2.9 2.9 2.8 2.8 平滑因子α1/α2 0.28/0.28 0.28/0.24 0.18/0.25 0.27/0.25 0.29/0.23 0.25/0.22 表 3 模拟实验两种方法反演结果与真值的比较
Table 3 Comparison of the Inversion Results of Two Methods with True Values for Simulation Experiments
方法 参数 实验1 实验2 实验3 实验4 实验5 实验6 OSS法 最大滑动量/m 0.222 0.232 0.276 0.224 0.266 0.188 平均滑动量/m 0.007 0.011 0.012 0.009 0.013 0.007 TSS法 最大滑动量/m 0.084 0.138 0.099 0.094 0.101 0.077 平均滑动量/m 0.001 0.003 0.005 0.004 0.004 0 TSS较OSS提升比 最大滑动量/% 9.37 6.38 12.05 8.80 11.16 7.38 平均滑动量/% 2.02 2.74 2.23 1.71 3.06 2.29 均方根误差/% 10.00 6.67 6.67 6.67 6.67 6.67 表 4 模拟实验特征值位置与TSS法优势条件之间的关系
Table 4 Relationship Between the Location of Eigenvalues and the Dominant Conditions of TSS Method in Simulation Experiments
条件 特征值位置 实验1 实验2 实验3 实验4 实验5 实验6 满足${\lambda _i} < - {\alpha _2}{R_i}$ 1~737 1~739 1~739 1~739 1~738 1~387 满足${\lambda _i} > - {\alpha _1}{T_i}$ 762~800 767~800 761~800 763~800 763~800 411~450 注:特征值位置是指在特征值矩阵中特征值沿着对角线从左上到右下排列所对应的位置 表 5 芦山地震断层几何参数及滑动参数
Table 5 Geometric Parameters and Slip Parameters of Lushan Earthquake Fault
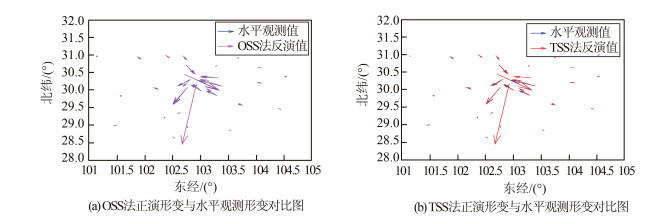
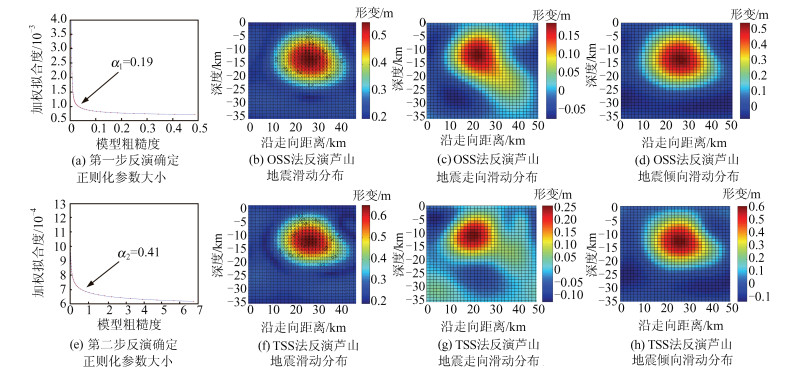
来源 滑动角/(°) 最大滑动量/m 断层长度/m 矩张量/(1019 N·m) 矩震级 数据拟合度 均匀滑动 80.13 0.75 21.94 0.72 Mw6.54 — TSS法 70.62 0.65 51 1.19 Mw6.68 0.763 OSS法 70.37 0.55 51 1.07 Mw6.65 0.741 文献[21] 71 0.91 31.2 0.53 Mw6.45 — 文献[22] — 1.59 — 1.54 Mw6.7 — 文献[23] 71 0.61 46 0.95 Mw6.6 — USGS 93 — — — Mw6.5 — CENC 95 — — — — — 注:USGS为美国地质调查局(United States Geological Survey),CENC为中国地震台网中心(China Earthquake Networks Center) -
[1] 许才军, 邓长勇, 周力璇.利用方差分量估计的地震同震滑动分布反演[J].武汉大学学报·信息科学版, 2016, 41(1):37-44 http://ch.whu.edu.cn/CN/abstract/abstract3431.shtml Xu Caijun, Deng Changyong, Zhou Lixuan. Coseismic Slip Distribution Inversion Method Based on Variance Component Estimation[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1):37-44 http://ch.whu.edu.cn/CN/abstract/abstract3431.shtml
[2] Funning G, Parsons B, Wright T, et al. Surface Displacements and Source Parameters of the 2003 Bam (Iran) Earthquake from Envisat Advanced Synthetic Aperture Radar Imagery[J]. Journal of Geophysical Research:Solid Earth, 2005, 110(B9):1-23 doi: 10.1029/2004JB003338/full
[3] 许才军, 刘洋, 温扬茂.利用GPS资料反演汶川Mw7.9级地震滑动分布[J].测绘学报, 2009, 38(3):195-201 doi: 10.3321/j.issn:1001-1595.2009.03.002 Xu Caijun, Liu Yang, Wen Yangmao. Mw7.9 Wenchuan Earthquake Slip Distribution Inversion from GPS Measurements[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3):195-201 doi: 10.3321/j.issn:1001-1595.2009.03.002
[4] 张国宏, 屈春燕, 宋小刚, 等.基于InSAR同震形变场反演汶川Mw7.9地震断层滑动分布[J].地球物理学报, 2010, 53(2):269-279 doi: 10.3969/j.issn.0001-5733.2010.02.005 Zhang Guohong, Qu Chunyan, Song Xiaogang, et al. Slip Distribution and Source Parameters Inverted from Coseismic Deformation Derived by InSAR Technology of Wenchuan Mw7.9 Earthquake[J]. Chinese Journal of Geophysics, 2010, 53(2):269-279 doi: 10.3969/j.issn.0001-5733.2010.02.005
[5] Jiang Z, Wang M, Wang Y, et al. GPS Constrained Coseismic Source and Slip Distribution of the 2013 Mw6.6 Lushan, China, Earthquake and Its Tectonic Implications[J]. Geophysical Research Letters, 2014, 41(2):407-413 doi: 10.1002/2013GL058812
[6] Okada Y. Surface Deformation to Shear and Tensile Faults in a Half Space[J]. Bulletin of the Seismological Society of America, 1985, 75(4):1135-1154 http://gji.oxfordjournals.org/cgi/ijlink?linkType=ABST&journalCode=ssabull&resid=75/4/1135
[7] Okada Y. Internal Deformation Due to Shear and Tensile Fault in a Half Space[J]. Bulletin of the Seismological Society of America, 1992, 92(2):1018-1040 http://gji.oxfordjournals.org/cgi/ijlink?linkType=ABST&journalCode=ssabull&resid=75/4/1135
[8] 孙建宝, 徐锡伟, 沈正康, 等.基于线弹性位错模型及干涉雷达同震形变场反演1997年玛尼Mw7.5级地震参数-Ⅰ均匀滑动反演[J].地球物理学报, 2007, 50(4):1097-1110 doi: 10.3321/j.issn:0001-5733.2007.04.017 Sun Jianbao, Xu Xiwei, Shen Zhengkang, et al. Parameter Inversion of the 1997 Mani Earthquake from InSAR Co-seismic Deformation Field Based on Linear Elastic Dislocation Model-Ⅰ Uniform Slip Inversion[J]. Chinese Journal of Geophysics, 2007, 50(4):1097-1110 doi: 10.3321/j.issn:0001-5733.2007.04.017
[9] 王乐洋, 许才军, 温扬茂.利用STLN和InSAR数据反演2008年青海大柴旦Mw6.3级地震断层参数[J].测绘学报, 2013, 42(2):168-176 http://d.old.wanfangdata.com.cn/Periodical/chxb201302002 Wang Leyang, Xu Caijun, Wen Yangmao. Fault Parameters of 2008 Qinghai Dachaidan Mw6.3 Earthquake from STLN Inversion and InSAR Data[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2):168-176 http://d.old.wanfangdata.com.cn/Periodical/chxb201302002
[10] 王乐洋, 李海燕, 温扬茂, 等.地震同震滑动分布反演的总体最小二乘方法[J].测绘学报, 2017, 46(3):307-315 http://d.old.wanfangdata.com.cn/Periodical/chxb201703006 Wang Leyang, Li Haiyan, Wen Yangmao, et al. Total Least Squares Method Inversion for Co-seismic Slip Distribution[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3):307-315 http://d.old.wanfangdata.com.cn/Periodical/chxb201703006
[11] 王乐洋.基于总体最小二乘的大地测量反演理论及应用研究[D].武汉: 武汉大学, 2011 http://www.cqvip.com/QK/90069X/201204/42958757.html Wang Leyang. Research on Theory and Application of Total Least Squares in Geodetic Inversion[D]. Wuhan: Wuhan University, 2011 http://www.cqvip.com/QK/90069X/201204/42958757.html
[12] 王乐洋, 许才军, 鲁铁定.病态加权总体最小二乘平差的岭估计解法[J].武汉大学学报·信息科学版, 2010, 35(11):1346-1350 http://ch.whu.edu.cn/CN/abstract/abstract1110.shtml Wang Leyang, Xu Caijun, Lu Tieding. Ridge Estimation Method in Ill-posed Weight Total Least Squares Adjustment[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11):1346-1350 http://ch.whu.edu.cn/CN/abstract/abstract1110.shtml
[13] 王乐洋, 于冬冬.病态总体最小二乘问题的虚拟观测解法[J].测绘学报, 2014, 43(6):575-581 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=chxb201406004 Wang Leyang, Yu Dongdong. Virtual Observation Method to Ill-posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6):575-581 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=chxb201406004
[14] Fan Q, Xu C, Yi L, et al. Implication of Adaptive Smoothness Constraint and Helmert Variance Component Estimation in Seismic Slip Inversion[J]. Journal of Geodesy, 2017, 91(10):1163-1177 doi: 10.1007/s00190-017-1015-0
[15] 王振杰, 欧吉坤, 柳林涛.一种解算病态问题的方法——两步解法[J].武汉大学学报·信息科学版, 2005, 30(9):821-824 http://ch.whu.edu.cn/CN/abstract/abstract2283.shtml Wang Zhenjie, Ou Jikun, Liu Lintao. A Method for Solving Ill-posed Problems-Two Step Method[J]. Geomatics and Information Science of Wuhan University, 2005, 30(9):821-824 http://ch.whu.edu.cn/CN/abstract/abstract2283.shtml
[16] Jonsson S. Fault Slip Distribution of the 1999 Mw7.1 Hector Mine, California, Earthquake, Estimated from Satellite Radar and GPS Measurements[J]. Bulletin of the Seismological Society of America, 2002, 92(4):1377-1389 doi: 10.1785/0120000922
[17] 王振杰, 欧吉坤.用L-曲线法确定岭估计中的岭参数[J].武汉大学学报·信息科学版, 2004, 29(3):235-238 http://ch.whu.edu.cn/CN/abstract/abstract4657.shtml Wang Zhenjie, Ou Jikun. Determination of Ridge Parameters in Ridge Estimation by L-Curve Method[J]. Geomatics and Information Science of Wuhan University, 2004, 29(3):235-238 http://ch.whu.edu.cn/CN/abstract/abstract4657.shtml
[18] Hansen P, O'Leary D. The Use of the L-Curve in the Regularization of Discrete Ill-posed Problems[J]. SIAM Journal on Scientific Computing, 1993, 14(6):1487-1503 doi: 10.1137/0914086
[19] 杨文采.地球物理反演和地震层析成象[M].北京:地质出版社, 1989 Yang Wencai. Geophysical Inversion and Seismic Tomography[M]. Beijing:Geological Publishing House, 1989
[20] Wang C, Ding X, Li Q, et al. Adaptive Regularization of Earthquake Slip Distribution Inversion[J]. Tectonophysics, 2016, 675:181-195 doi: 10.1016/j.tecto.2016.03.018
[21] 刘云华, 汪驰升, 单新建, 等.芦山Ms7.0级地震InSAR形变观测及震源参数反演[J].地球物理学报, 2014, 57(8):2495-2506 http://www.cqvip.com/QK/94718X/20148/662244307.html Liu Yunhua, Wang Chisheng, Shan Xinjian, et al. Result of SAR Differential Interferometry for the Co-seismic Deformation and Source Parameter of the Ms7.0 Lushan Earthquake[J]. Chinese Journal of Geophysics, 2014, 57(8):2495-2506 http://www.cqvip.com/QK/94718X/20148/662244307.html
[22] 王卫民, 郝金来, 姚振兴. 2013年四川芦山地震震源破裂过程反演初步结果[J].地球物理学报, 2013, 56(4):1412-1417 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqwlxb201304036 Wang Weimin, Hao Jinlai, Yao Zhenxing. Preliminary Result for Rupture Process of 2013, Lushan Earthquake, Sichuan, China[J]. Chinese Journal of Geophysics, 2013, 56(4):1412-1417 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqwlxb201304036
[23] Wang M, Jia D, Shaw J, et al. The 2013 Lushan Earthquake:Implications for Seismic Hazards Posed by the Range Front Blind Thrust in the Sichuan Basin, China[J]. Geology, 2014, 42(10):915-918 doi: 10.1130/G35809.1
-
期刊类型引用(16)
1. 祝意青,赵云峰,隗寿春,张国庆,刘芳. 2022年青海门源M_S6.9和四川泸定M_S6.8地震震中的精准判定及思考. 地震地质. 2025(01): 235-245 .  百度学术
百度学术
2. 王伟力,郑兵,郝洪涛,温军军,刘宏伟,马伶俐,廖明辉. 四川地区流动重力观测及其在地震预测中的应用. 大地测量与地球动力学. 2024(01): 89-94 .  百度学术
百度学术
3. 杨雄,祝意青,赵云峰,隗寿春,操聪,吕宏斌,曾亚光. 2020年伽师M_S6.4地震前后重力变化. 大地测量与地球动力学. 2024(03): 277-282 .  百度学术
百度学术
4. 艾力夏提·玉山,刘代芹,阿卜杜塔伊尔·亚森,陈丽,李杰,赵磊,李秉烨. 北天山流动重力测网场源分辨能力. 大地测量与地球动力学. 2024(03): 272-276 .  百度学术
百度学术
5. 李树鹏,胡敏章,祝意青,朱成林,崔华伟,陆汉鹏,张刚,王锋吉. 不同类型地震震级与重力变化异常的统计特征及其机理分析. 地球物理学报. 2024(08): 3032-3059 .  百度学术
百度学术
6. 李树鹏,胡敏章,祝意青,郝洪涛,殷海涛,贾媛,崔华伟,陆汉鹏,张刚,王锋吉,刘洪良. 2023年山东平原M_S5.5地震前重力变化. 地震地质. 2024(05): 1172-1191 .  百度学术
百度学术
7. 梁霄,储飞,徐如刚,孙鸿博,肖伟鹏,王俊. 2014年霍山M_S4.3地震前后重磁场变化特征及机理分析. 地震地质. 2024(05): 1151-1171 .  百度学术
百度学术
8. 孔祥魁,刘代芹,艾力夏提·玉山,李杰,陈丽,李瑞,陈荣柳. 乌鲁木齐及周边地区重力场及视密度变化特征. 地震地质. 2024(05): 1123-1150 .  百度学术
百度学术
9. 李秉烨,艾力夏提·玉山,刘代芹,陈丽,阿卜杜塔伊尔·亚森,阿尔达克·卡德尔别克,赵磊. 乌什M_S7.1地震重力场变化特征分析研究. 内陆地震. 2024(04): 366-375 .  百度学术
百度学术
10. 赵云峰,祝意青,隗寿春,郑兵,刘芳,杨雄,毛经伦,孙和平. 基于重力数据的2022年青海门源M_S 6.9及四川泸定M_S 6.8地震预测. 科学通报. 2023(16): 2116-2123 .  百度学术
百度学术
11. 付广裕. 中国地震重力研究现状及其面临的挑战. 武汉大学学报(信息科学版). 2023(06): 858-869 .  百度学术
百度学术
12. 郑家军,李铂,朱成林,黄金水,杨立涛,董敏,熊玮,韩博,刘海林,池国民,吴婧. 2022年青州M_L4.1地震前后的重力场变化分析. 地震. 2023(03): 102-119 .  百度学术
百度学术
13. 杨雄,祝意青,赵云峰,隗寿春. 2021年漾濞M_S6.4地震前后重力场动态特征分析. 地震学报. 2023(05): 863-874 .  百度学术
百度学术
14. Jin Wei,Huining Huang,Ying Jiang,Ziwei Liu. Abnormal characteristics and effectiveness evaluation of the micro-seismic signal before the Debao M_S4.8 earthquake. Geodesy and Geodynamics. 2023(06): 605-613 .  必应学术
必应学术
15. 祝杰,李婉秋,陶志刚,刘洋洋,马未宇. 青海门源M_S6.9地震震前OLR异常与InSAR同震形变关联性分析. 中国地震. 2023(04): 857-867 .  百度学术
百度学术
16. 许才军,王晓航,温扬茂,李伟. 地震大地测量确定凹凸体研究进展与展望. 武汉大学学报(信息科学版). 2022(10): 1701-1712 .  百度学术
百度学术
其他类型引用(4)





 下载:
下载: