文章信息
- 叶敏, 王斌, 王思远, 刘长征, 李艳霞, 岑炜
- YE Min, WANG Bin, WANG Siyuan, LIU Changzheng, LI Yanxia, CEN Wei
- 多特征分量结合的WorldView-3影像建筑容积率分类提取
- Extracting Floor Area Ratio of the Classified Buildings from Very High Resolution Satellite Image Using Multiple Features
- 武汉大学学报·信息科学版, 2019, 44(11): 1674-1684
- Geomatics and Information Science of Wuhan University, 2019, 44(11): 1674-1684
- http://dx.doi.org/10.13203/j.whugis20180241
-
文章历史
收稿日期: 2018-08-16

2. 中国科学院遥感与数字地球研究所数字地球重点实验室, 北京, 100094;
3. 中国科学院大学, 北京, 100045;
4. 石河子大学信息科学与技术学院, 新疆 石河子, 832003
2. Key Laboratory of Digital Earth Science, Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100094, China;
3. Chinese Academy of Sciences University, Beijing 100045, China;
4. School of Information Science and Technology, Shihezi University, Shihezi 832003, China
对于城市规划与管理而言,城市建筑容积率(floor area ratio,FAR)的大小直接反映了城市居住环境的优劣,是城市发展注重城市环境质量和可持续发展的标志[1]。由于容积率日益受到城市规划部门、房地产开发商和广大居民的关注,因此对城市现状容积率的调查就显得尤为重要[2]。在城市容积率规划与管理中,分公益性用地与商业性用地两大类进行,其中,商业性用地容积率是规划与管理的重点,包括居住类、商业商务类以及工业类等[3]。因此,实现城市现状建筑容积率分类提取对于制定科学合理的控制性详细规划及控制城市用地开发过程中的容积率具有重要的现实意义。
目前,利用遥感技术提取建筑物容积率的方法分为两种。一种是非成像方法,即不获取目标对象的遥感影像,而直接获取反映目标对象空间信息的参数等方法,如机载激光扫描技术[4]。另一种是成像方法,该方法根据容积率提取原理的不同,可分为以下3种情况:(1)借助合成孔径雷达技术,基于雷达影像的后向散射值数据得到建筑物的高度、建筑面积等信息,从而计算建筑容积率[5];(2)借助摄影测量技术,基于建筑物在影像中的二维坐标,通过立体像对密集匹配得到建筑物三维坐标,从而计算建筑容积率[6-8];(3)借助卫星影像,利用建筑物阴影信息间接得到建筑容积率。在借助阴影信息的容积率提取方法中,可分为阴影面积法[2, 9]与阴影长度法[10-11]两种。其中,阴影面积法通过提取建筑物的阴影面积,并回归分析直接得到建筑面积,从而计算得到容积率;阴影长度法通过提取建筑物的阴影长度,借助太阳高度角信息反算建筑物高度,进而估算建筑物楼层数,最终结合建筑面积计算得到容积率。
机载激光扫描技术与合成孔径雷达技术可实现建筑容积率的高精度获取,但数据处理过程相对复杂,且数据的获取成本较高;摄影测量技术提取建筑容积率存在不同程度的缺陷,包括需要多源数据的结合、精度与适用范围不能兼顾等。目前,以WorldView-3为代表的高端对地观测卫星具备极高的空间分辨率,极强的机动获取能力和极广的观测谱段[12],借助高分辨率卫星影像提取建筑容积率具有经济、快速、容积率解算简便等优势,是一种大范围、高精度且高效、经济的城市现状建筑物容积率提取手段。在借助高分辨率卫星影像,通过阴影信息提取建筑容积率方面,文献[2, 9]通过提取阴影面积得到建筑容积率,但所得容积率并未对应具体类别的建筑物,后续容积率相关分析则基于目视判别进行;文献[10-11]通过提取阴影长度与建筑物基地面积得到建筑容积率,但在提取建筑物基地面积上均采用在Arcmap中勾画建筑物基地轮廓的方法,且所得容积率也未对应具体类别的建筑物。
针对以上建筑容积率提取方法上的优势与不足,为实现商业性用地现状容积率分类提取,本文以北京市为例,借助高分辨率卫星影像,提出了一种多特征分量(主成分分量、主方向、边界指数以及矩形拟合度)相结合的面向对象建筑容积率分类提取方法,通过利用阴影与不同类型建筑物对象的光谱和几何特征,实现阴影与不同类型建筑物对象分类提取。鉴于当前文献中未有对卫星影像提取容积率中阴影面积法与阴影长度法计算精度的定量对比分析,本文通过实地逐一调研各建筑容积率,并对比阴影面积法与阴影长度法下的容积率计算精度,完成建筑容积率的分类提取。
1 容积率提取方法本文提出的建筑容积率分类提取方法的整体思路是:首先对影像实施主成分变换,对变换后的图像进行多尺度分割,得到影像对象;然后分层选取分类所需的特征分量与样本对象,输入朴素贝叶斯网络分类器进行学习,用于提取阴影和建筑物两类对象;最后从阴影和建筑物对象中得到阴影面积、建筑物的高度、建筑物基底面积和建筑面积等信息,并分别运用阴影面积法与阴影长度法计算建筑容积率。具体技术流程见图 1。
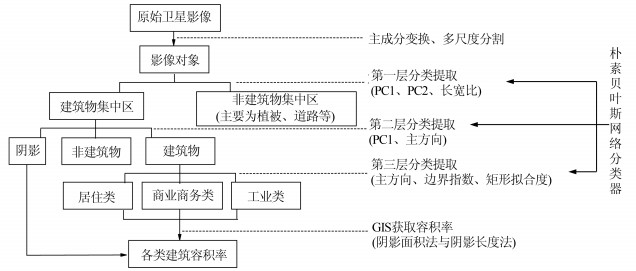
|
| 图 1 容积率提取技术流程图 Fig. 1 Flowchart of Floor Area Ratio Extraction |
在选取特征分量前,需要依据各类对象的自身特点以及相互间的特征差异来综合选取最优分类特征。本文对目标对象的分类提取主要基于光谱与几何两大类特征。
1.1.1 光谱特征——主成分PC1、PC2主成分分析(principal component analysis,PCA)是一种对原始影像像元作特征变换,从而除去波段之间的多余信息,将多波段的影像信息压缩到比原波段更有效的少数几个波段的影像处理方法。图 2为经过主成分变换后几类典型地物在各分量下的光谱特征曲线,可以看出,在第一和第二主成分分量下(PC1、PC2),几类地物之间具有明显区分度,而在第三和第四分量(PC3、PC4)下,各类地物之间的差异表现十分不明显,表明第一和第二主成分分量包含原始影像中绝大部分不同地物之间的差异信息,而第三和第四分量则主要为噪声信息,不利于影像的分类。因此本文选取第一和第二主成分分量为输出波段,舍去第三和第四分量。
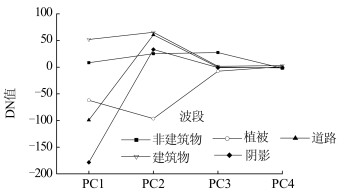
|
| 图 2 主成分变换后几类典型地物的光谱特征曲线 Fig. 2 Spectral Curves of Five Ground Features After PCA Rotation |
为突出阴影像元与其他非阴影类像元间第一主成分特征,需要将不同阈值范围内的各类像元统一至相同范围进行对比。本文采用线性归一化方法,归一化公式为:
| $y=\frac{x-{{D}_{\text{min}}}}{{{D}_{\text{max}}}-{{D}_{\text{min}}}}$ | (1) |
其中,x和y分别为归一化前后像元值(digital number, DN);Dmax和Dmin分别为特征分量下的最大、最小DN值。
图 3为归一化后的第一主成分下采样数据的亮度直方图,可以看出,阴影类像元亮度值波动范围相比于其他非阴影类像元而言相当小(0.01~0.09),说明该区间内集中了丰富的阴影信息,充分利用阴影类像元在第一主成分分量下的光谱特征可以有效将影像中阴影与非阴影对象区分开。
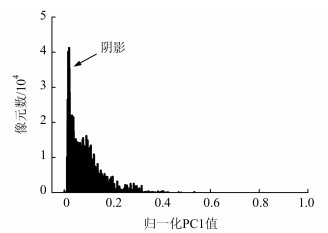
|
| 图 3 PC1分量亮度直方图 Fig. 3 Histogram of Normalized PC1 |
主方向(main direction,MD)是平面几何对象的一个基本形状特征。在图像处理中,该特征取决于对象边界轮廓像元在像元平面的空间分布。主方向特征的取值范围为[0°, 180°]。在第一层提取建筑物集中区和第二层提取阴影和建筑物两类对象中,主方向是一个重要特征,该特征充分利用了卫星影像中的光照信息,即太阳高度角与太阳方位角。在一景影像中,建筑物与阴影分别保持各自不同的朝向,反映到影像对象上即有各自不同的主方向,因此主方向是阴影和建筑物两类对象与其他对象在几何形状方面表现最为突出的特征之一。
边界指数(border index,BI)用于描述几何对象边界的锯齿状程度,其取值范围为[1,+∞),取值为1表明对象边界达到无锯齿的理想状态,值越大, 表明对象边界锯齿状现象越明显。
矩形拟合度(rectangular fit,RF)用于描述几何对象与矩形的拟合程度,其取值范围为[0, 1],取值为0表明对象与矩形不拟合,取值为1表明对象与矩形完全拟合。相对而言,研究区域内的居住类建筑物对象表现为顶面边界指数较高且矩形拟合度较低;商业商务类由于建筑物设计构型复杂,因而较居住类而言表现为顶面边界指数更高,矩形拟合度更低;工业类建筑由于其顶面整齐划一且多为规则矩形,因此表现为顶面边界指数较低,矩形拟合程度较高。
表 1为阴影与建筑物两类对象的特征描述以及对应特征值的统计结果,可定量表现各对象特征与其间差异。为体现边界指数与矩形拟合度特征在不同研究区域内具有普适性,本文另外选取两幅与研究区域范围大小相同、影像获取时间相同的影像,并对其中的居住类、商业商务类以及工业类建筑对象的边界指数与矩形拟合度特征进行描述与统计,结果如表 2所示。从表 2可以看出,就本文实验区而言,两幅对比影像与本文影像中居住类、商业商务类以及工业类建筑的边界指数与矩形拟合度特征具有高度相似性,表明边界指数与矩形拟合度特征在不同研究区域内具有普适性。
| 对象类别 | 特征描述(特征值集中范围) | |||||
| 第一主成分均值 | 第一主成分方差 | 主方向 | 边界指数 | 矩形拟合度 | ||
| 阴影 | 低 (-170, -70) |
低 (36, 96) |
主要集中为西北、东西、南北3个方向 (0°, 45°)、(70°, 90°)、(160°, 180°) |
|||
| 建筑物 | 居住类 | 较高 (50, 330) |
高 (150, 350) |
主要集中为东北、南北两个方向 (0°, 45°)、(80°, 95°) |
较高 (1, 1.8) |
较低 (0.78, 0.95) |
| 商业商务类 | 较高 (0, 280) |
较高 (50, 250) |
主要集中为东西、南北两个方向 (80°, 100°)、(160°, 175°) |
高 (1.2, 2.7) |
低 (0.61, 0.91) |
|
| 工业类 | 高 (150, 400) |
低 (40, 120) |
主要集中为东西、南北两个方向 (75°, 95°)、(165°, 180°) |
低 (1.1, 1.4) |
高 (0.92, 0.99) |
|
| 对象 | 特征描述(特征值集中范围) | |||||||
| 边界指数 | 矩形拟合度 | |||||||
| 影像1 | 影像2 | 本文影像 | 影像1 | 影像2 | 本文影像 | |||
| 建筑物 | 居住类 | 较高(1, 2.6) | 较高(1.2, 2.5) | 较高(1, 1.8) | 较低(0.50, 1.00) | 较低(0.70, 0.93) | 较低(0.78, 0.95) | |
| 商业商务类 | 高(1.4, 3.3) | 高(1.1, 4.7) | 高(1.2, 2.7) | 低(0.30, 0.95) | 低(0.47, 0.90) | 低(0.61, 0.91) | ||
| 工业类 | 低(1.1, 1.8) | 低(1.2, 1.6) | 低(1.1, 1.4) | 高(0.96, 0.99) | 高(0.95, 0.99) | 高(0.92, 0.99) | ||
遥感数据贝叶斯网络分类器的结构总体上可有两种考虑:(1)忽略特征间相关性,直接指定所有特征节点为类节点的子节点,即朴素贝叶斯网络分类器;(2)考虑特征间相关性,并从样本数据中学习获得网络结构及节点参数。它们的不同之处主要在于对特征间相关性的不同考虑,由此导致具有不同网络结构的分类器模型。朴素贝叶斯网络分类器由于不考虑特征之间的相关性,其网络结构已确定,因而在遥感影像分类的实际应用中具有较大优势,同时可以在仅需少量样本数据的情况下仍然表现出很好的性能和稳定性[13]。因此,本文对影像实施主成分变换,以满足应用朴素贝叶斯网络分类器的前提条件,即不考虑特征之间的相关性。各层特征分量间的相关系数如表 3所示。
| 分类层次 | 特征分量 | 第一主成分均值 | 第二主成分均值 | 第一主成分方差 | 第二主成分方差 | 长宽比 |
| 第一层 | 第一主成分均值 | 1 | -0.31 | 0.61 | 0.14 | 0.09 |
| 第二主成分均值 | 1 | -0.15 | -0.68 | 0.09 | ||
| 第一主成分方差 | 1 | 0.23 | 0.06 | |||
| 第二主成分方差 | 1 | -0.12 | ||||
| 长宽比 | 1 | |||||
| 分类层次 | 特征分量 | 第一主成分均值 | 第二主成分均值 | 主方向 | ||
| 第二层 | 第一主成分均值 | 1 | 0.67 | -0.06 | ||
| 第二主成分均值 | 1 | -0.07 | ||||
| 主方向 | 1 | |||||
| 分类层次 | 特征分量 | 主方向 | 边界指数 | 矩形拟合度 | ||
| 第三层 | 主方向 | 1 | -0.05 | 0.01 | ||
| 边界指数 | 1 | -0.74 | ||||
| 矩形拟合度 | 1 |
遥感影像的朴素贝叶斯网络分类器对给定的输入样本数据,通过学习得到描述特征变量与类别变量的分布参数,并计算后验概率分布,最后以后验概率最大类为输出类别。设特征变量F的集合
| $ \begin{align} & \ \ \ \ \ \ \ \ \ \ P\left( C={{c}_{k}}|F=f \right)\text{=} \\ & \frac{P\left( C={{c}_{k}} \right)\prod\limits_{i=1}^{m}{P\left( {{F}_{i}}=f_{\text{j}}^{i}|C={{c}_{k}} \right)}}{\prod\limits_{i=1}^{m}{P\left( {{F}_{i}}=f_{\text{j}}^{i} \right)}} \\ \end{align} $ | (2) |
式中,
本文所用的朴素贝叶斯网络分类器在对特征变量的参数学习中,基于样本数据来估计描述特征变量与类别变量的分布参数,因此参数估计采用最大似然估计法[13]。
| $ \begin{align} & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P\left( C={{c}_{k}} \right)=\frac{{{N}_{k}}}{N} \\ & P\left( {{F}_{i}}=f_{j}^{i}|C={{c}_{k}} \right)=\frac{\sum\limits_{i=1}^{m}{I\left( {{F}_{i}}=f_{l}^{i},\text{ }~\text{ }C={{c}_{k}} \right)}}{{{N}_{k}}} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( l=1,\text{ }~\text{ }2\ldots j \right) \\ \end{align} $ | (3) |
式中,N为样本总数;Nk为ck类样本总数;I为指示函数;
以后验概率最大为准则,即:
| $ \text{arg }~\text{ }\underset{{{c}_{k}}}{\mathop{\text{max}}}\,\text{ }~\text{ }P\left( C={{c}_{k}} \right)\prod\limits_{i=1}^{m}{P\left( {{F}_{i}}=f_{j}^{i}|C={{c}_{k}} \right)} $ | (4) |
来判断对象的输出类[14]。
1.3 容积率推导容积率即地块以上范围内地面以上总建筑面积与地块总用地面积的比值,为无量纲值,计算公式为:
| $ R=F/A $ | (5) |
式中,R为容积率;F为地块内总建筑面积;A为地块面积。地块面积A可直接通过人工编辑操作获得,地块内总建筑面积为地块内所有建筑的建筑面积总和。因此计算容积率的关键在于计算建筑面积。
1.3.1 阴影面积法对于在高度上表现规则(即每一楼层的建筑面积相等)的建筑物而言,其建筑面积可通过基底面积与楼层数的乘积获得。设每个建筑物覆盖的基底面积为ai,包含楼层数为Ni,则单个建筑的建筑面积Fi的计算公式为:
| $ {{F}_{i}}={{a}_{i}}\times {{N}_{i}} $ | (6) |
假设单个建筑的建筑面积Fi与对应阴影面积Si线性相关,则可建立两者之间的线性关系式:
| $ {{F}_{i}}=a{{S}_{i}}+b $ | (7) |
其中,a和b需结合实际数据通过回归分析计算得到。运用已知的回归方程和提取的阴影面积,便可计算该街区建筑面积,进而得到容积率。
1.3.2 阴影长度法在阴影长度法提取容积率中,关键在于获取建筑物层数,可通过提取建筑物阴影,计算阴影长度,结合太阳高度角信息,反算建筑物高度,最后除以建筑物层高,得到建筑物层数。单个建筑的建筑面积Fi计算公式为:
| $ {{F}_{i}}={{N}_{i}}\times {{f}_{i}} $ | (8) |
| $ {{N}_{i}}={{H}_{i}}/d $ | (9) |
| $ {{H}_{i}}={{L}_{i}}\text{tan }\!\!~\!\!\text{ }\theta $ | (10) |
式中,Ni为建筑物层数;fi为建筑物基底面积;Hi为建筑物高度;d为建筑物层高;Li为建筑物阴影长度;θ为太阳高度角。
2 容积率分类提取实验与分析 2.1 研究区域及数据本文选取一幅WorldView-3卫星影像进行建筑容积率提取实验。研究区域位于北京市房山区长阳镇部分片区,面积为5.76 km2。影像拍摄于2014年10月18日,包含4个波段,多光谱影像分辨率为1.2 m,全色影像分辨率为0.3 m,太阳高度角为39.5°,太阳方位角为163.5°。在正式进行实验前,已完成对影像的预处理,包括影像的配准、几何校正及融合等流程。
2.2 主成分变换本文借助遥感影像处理软件ENVI 5.3完成对实验影像的主成分变换。
原始影像包含蓝(blue, B)、绿(green, G)、红(red, R)、近红外(near infrared, NIR)4个波段,主成分变换后输出影像同样包含4个波段,分别是第一、二、三、四主成分的数据,如图 4所示。

|
| 图 4 各波段影像对比 Fig. 4 Comparison of Images of All Bands |
从图 4中可以观察到,阴影在蓝、绿、红3个波段的响应并不十分明显,而在近红外波段则表现突出。根据文献[15]对阴影检测的研究结果,由于瑞利散射,卫星传感器接收阴影区域的辐射量随着波长的增加而减少,因此相比于可见光波段,通过近红外波段来区分阴影与非阴影区域要更加容易。同时,原始影像完成主成分变换后,第一、二主成分对应的影像可以清楚区分阴影与非阴影区域,第三、四成分则不然。由表 4可知,第一主成分包含原始影像82.5%的信息,第二主成分包含15.1%[16],两主成分共同包含原始影像97.6%的信息量,因此本文将第三、四波段作为噪声波段舍去,选取第一、二主成分波段作为输出波段,用于后续容积率提取。
| 项目 | PC1 | PC2 | PC3 | PC4 |
| 信息量占比 | 82.5 | 15.1 | 2.3 | 0.1 |
在进行影像分割前,需要综合研究区域状况,结合提取需求设置各项分割参数,包括影像各波段权重、分割尺度、形状因子及紧致度等。波段权重根据第一、第二主成分的信息量大小按比例确定;分割尺度按照每一层所要提取的对象不同,遵循适当过分割的原则,分割尺度的选取以确保各分类对象可相互分割开并且各自保持较好的完整性为依据,并通过观察最终确定出最佳分割尺度[17];形状因子与紧致度按照软件默认设置。
分割设置的具体参数如表 5所示。
| 分类提取层次 | 波段权重 (PC1:PC2) |
分割尺度 | 形状因子 | 紧致度 |
| 第一层 | 5:1 | 1 000 | 0.1 | 0.5 |
| 第二层 | 5:1 | 150 | 0.1 | 0.5 |
| 第三层 | 5:1 | 100 | 0.1 | 0.5 |
在样本对象选取上,本文采用分层抽样方法。在确定样本容量方面,文献[18]指出,比例分层抽样具有能提高估计值的精度和确保分层群体比例的代表性等诸多优势,本文采用比例分层的抽样方法,辅以系统抽样方法进行样本选取。
在每一层分类中,首先随机采样,分别统计出各类样本对象对应的各个特征变量值,利用式(1)将所有变量值归一化,对比归一化后特征变量值的方差,选取方差最大对应特征作为该类对象的分类依据。类别数即为分类依据下的特征变量值集中范围个数。类别数确定后,统计各类别下对应的总体数目,最后按照总体数目30%[19]的比例确定最终样本抽取的数量,即样本容量。对于无明显集中范围,即变量值呈单一线性变化时,采用系统抽样方法抽取样本。
选取的样本信息如表 6所示。
| 分类层次 | 对象 | 特征变量归一化方差比 | 分类依据 | 类别数 | 类别样本数比(样本数合计) |
| 第一层 | 第一主成分均值:第一主成分方差:第二主成分均值:第二主成分方差:长宽比 | ||||
| 植被 | 2:1:3:4:1 | 第二主成分方差 | 31 | 1:1:…:1(31) | |
| 道路 | 2:3:2:2:1 | 第一主成分方差 | 14 | 1:1:…:1(14) | |
| 建筑物集中区 | 3:1:3:3:5 | 长宽比 | 3 | 40:111:10(161) | |
| 第二层 | 第一主成分均值:第一主成分方差:主方向 | ||||
| 阴影 | 3:4:6 | 主方向 | 3 | 18:35:9(62) | |
| 建筑物 | 3:5:4 | 第一主成分方差 | 63 | 1:1:…:1(63) | |
| 非建筑物 | 7:4:92 | 主方向 | 3 | 70:136:65(271) | |
| 第三层 | 主方向:边界指数:矩形拟合度 | ||||
| 居住类 | 2:5:3 | 边界指数 | 3 | 5:30:13(48) | |
| 商业商务类 | 5:3:6 | 矩形拟合度 | 2 | 6:17(23) | |
| 工业类 | 8:3:2 | 主方向 | 2 | 23:13(36) |
在整个阴影与建筑物提取过程中,分为3个层次进行,首先根据每一层次所需提取出的目标对象的不同来选择分类特征以及样本对象,并用于分类器的学习,然后将训练后的分类器应用于未分类对象的分类。3个层次的对象分类均选用朴素贝叶斯网络分类器,因此整个过程使用了3个朴素贝叶斯分类器完成阴影与建筑物的提取,最终的提取结果如图 5所示。

|
| 图 5 分类结果 Fig. 5 Classification Results |
每一层分类提取的精度采用基于样本数据的精度评价方法,其中各层分类精度以及阴影、居住类、商业商务类和工业类建筑的提取精度分别如表 7和表 8所示。
| 指标 | 第一层 | 第二层 | 第三层 |
| 总体精度 | 0.9436 | 0.9140 | 0.9099 |
| Kappa系数 | 0.8898 | 0.8608 | 0.8550 |
| 对象 | 阴影 | 建筑物 | ||
| 居住类 | 商业商务类 | 工业类 | ||
| 生产精度 | 0.9341 | 0.9132 | 0.8926 | 0.9142 |
| 用户精度 | 0.8087 | 0.9187 | 0.8308 | 0.9425 |
需要指出的是,在第一层分类中,由于分割尺度较大,所得影像对象总体数目较少,对应样本数量较少,因此基于样本的精度评价结果较好,总体精度与Kappa系数表现较高,分别为0.943 6与0.889 8;对于顶面边界指数较大的建筑物而言,其侧面表现为较多凸出部分,凸出部分在建筑物侧面形成阴影,该部分对象极易错分为阴影对象,故阴影提取的生产精度较高,而用户精度较低,用户精度仅为0.808 7。
2.4 容积率计算及精度分析用阴影面积法计算容积率时,首先需要统计各建筑物对象所对应的阴影面积,然后对研究区域内所有建筑物的实际楼层数进行实地逐一调查,在Arcmap中通过人工编辑操作得到建筑物的实际基底面积及对应的实际阴影面积,根据实际楼层数与实际基底面积得到各社区单元内的实际建筑面积,最后根据实际阴影面积与实际建筑面积,结合式(5)~(7)拟合出线性回归方程,并用于计算阴影面积法下的容积率值。影像内社区单元示意图如图 6所示。
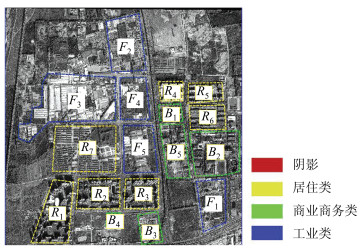
|
| 图 6 原始影像及社区单元示意图 Fig. 6 Original Image and General View of Community Unit |
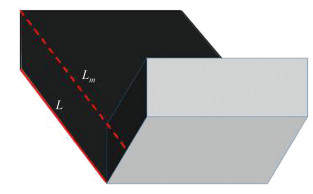
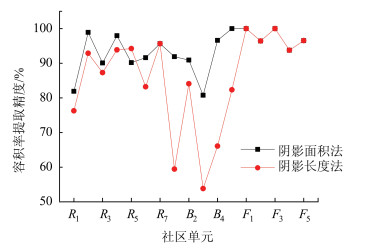
用阴影长度法计算容积率时,首先需要根据太阳高度角数据,构造一组满足太阳投射几何关系的平行线,该平行线将与各个阴影对象相交,然后分别以各阴影对象为单元,取各阴影对象范围内的阴影相交线的最大值,并乘上折减系数,所得结果作为阴影长度最终值。折减系数的计算原理如图 7所示。研究区域内建筑物满足图 7所示的阴影投射关系。上文已指出,在一景影像中,建筑物与阴影分别保持各自不同的朝向,因此,对于所有阴影对象而言,其实际阴影长度L与所截取的阴影长度最大值Lm有相同的折减系数,故在影像中选取一处在形状轮廓上与图 7最相近的阴影对象,并量取该对象的实际阴影长度L与所截取的阴影长度最大值Lm,两者比值即为折减系数。建筑物基底面积则通过统计建筑物顶面积可得,最后结合阴影长度,根据式(5)、式(8)~(10)计算阴影长度法下的容积率值,其中建筑物层高取住宅层高适宜高度2.8 m[20]。两种方法下的容积率计算结果以及对应的计算精度如表 9~11所示,容积率提取结果精度对比如图 8所示。
|
| 图 7 折减系数计算原理示意图 Fig. 7 Principle Diagram for Computing Reduction Factor |
| 研究区域 | 社区单元编号 | 实际容积率 | 阴影面积法 | 精度/% | 阴影长度法 | 精度/% |
| 居住类 | R1 | 2.32 | 2.74 | 81.90 | 1.77 | 76.29 |
| R2 | 1.83 | 1.85 | 98.91 | 1.96 | 92.90 | |
| R3 | 1.81 | 1.99 | 90.06 | 1.58 | 87.29 | |
| R4 | 2.45 | 2.40 | 97.96 | 2.30 | 93.88 | |
| R5 | 1.73 | 1.90 | 90.17 | 1.83 | 94.22 | |
| R6 | 1.43 | 1.55 | 91.61 | 1.67 | 83.22 | |
| R7 | 0.23 | 0.24 | 95.65 | 0.24 | 95.65 | |
| 平均精度 | 92.32 | 89.06 |
| 研究区域 | 社区单元编号 | 实际容积率 | 阴影面积法 | 精度/% | 阴影长度法 | 精度/% |
| 商业商务类 | B1 | 0.37 | 0.34 | 91.89 | 0.52 | 59.46 |
| B2 | 0.44 | 0.40 | 90.91 | 0.51 | 84.09 | |
| B3 | 0.26 | 0.31 | 80.77 | 0.38 | 53.85 | |
| B4 | 0.59 | 0.61 | 96.61 | 0.79 | 66.10 | |
| B5 | 0.68 | 0.68 | 100.00 | 0.80 | 82.35 | |
| 平均精度 | 92.04 | 69.17 |
| 研究区域 | 社区单元编号 | 实际容积率 | 阴影面积法 | 精度/% | 阴影长度法 | 精度/% |
| 工业类 | F1 | 0.17 | 0.17 | 100.00 | 0.17 | 100.00 |
| F2 | 0.28 | 0.29 | 96.43 | 0.29 | 96.43 | |
| F3 | 0.43 | 0.43 | 100.00 | 0.43 | 100.00 | |
| F4 | 0.16 | 0.17 | 93.75 | 0.17 | 93.75 | |
| F5 | 0.29 | 0.30 | 96.55 | 0.30 | 96.55 | |
| 平均精度 | 97.35 | 97.35 |
|
| 图 8 容积率提取结果精度对比 Fig. 8 Accuracy Comparison of FAR Extraction Results |
如表 9~11与图 8结果所示,不论在居住类还是商业商务类建筑物容积率估算上,阴影面积法较阴影长度法而言精度要高,原因在于阴影面积法计算容积率的精度仅取决于阴影面积的提取精度,而阴影长度法计算容积率的精度取决于阴影长度和基底面积的提取精度两个方面,误差来源更多,因而阴影长度法计算容积率的精度较低;在工业类方面,由于工业类建筑物绝大多数为单层建筑,且密集连续分布,在影像上表现为几乎没有阴影或阴影在软件中无法识别,在计算该类建筑物容积率上,阴影面积法与阴影长度法的处理原理一致,即建筑物顶面积之和与社区单元占地面积的比值,因此两种方法下的容积率计算结果与精度相同。
另外,观察表 9~11中数据可发现,两种方法下的容积率计算精度均表现为商业商务类显著低于居住类。对于阴影面积法而言,造成这一现象的主要原因为商业商务类建筑物数量与居住类相差较大(商业商务类包含77个建筑物对象,居住类包含160个建筑物对象),从回归分析的角度而言,用于拟合回归方程的实际数据量越多,回归方程的可靠性与估算结果的精确性越好,因此,商业商务类容积率估算精度显著低于居住类。另外,对于阴影长度法而言,由于在计算建筑物层数时,统一采用住宅层高2.8 m,而大多数商业商务类建筑物的层高与居住类表现出较大差异,势必会在计算商业商务类建筑物容积率时造成偏差。此外,由阴影长度法的计算原理可知,该方法适用于在高度上表现规则的建筑物,而商业商务类建筑物较居住类而言,有相当一部分表现为单栋建筑物分不同部分建造,各个部分之间楼层数不尽相同,高度上表现出不规则性,因而用阴影长度法计算商业商务类建筑物容积率的误差比在高度上规则性较高的居住类建筑物要大。
3 结语本文提出的多特征分量相结合的面向对象建筑容积率分类提取方法,通过利用建筑物与阴影对象的光谱和几何特征,实现了建筑容积率的分类提取,为城市现状建筑物容积率的分类提取提供了一种参考手段。在借助分类器进行影像分类上,现有研究对选择分类器的学习样本上叙述略显不足,而如何根据研究区域自身特点,选取最能反映目标对象特性的特征分量,并按照科学原则选取分类器学习样本,对于后续分类效果与精度表现上至关重要,故本文在特征分量与样本对象的选取上进行着重叙述,可为如何提高借助分类器进行影像分类方法的精度等方面的研究工作提供参考思路。
对阴影面积法与阴影长度法下的容积率分类计算结果进行分析可知,阴影面积法较阴影长度法,在容积率分类提取精度方面表现出较大优势。除阴影遮挡、地物情况复杂多变等实际情况中不可避免的共同影响外,阴影面积法的容积率计算误差仅来源于阴影面积的提取误差,而阴影长度法来源于阴影长度与建筑物基地面积的提取两个方面,误差来源更多,因而精度较阴影面积法而言要低。此外,城市区域范围内建筑物在高度上的情况复杂多变,主要表现为建筑物由不同高度的各部分构成以及不同类型建筑物间楼层高度存在差异。阴影长度法对于高度表现规则的建筑物更具适用性,但实际情况中并不能很好地满足这一条件,在使用条件上阴影长度法较阴影面积法更苛刻,故对于大范围分类提取包含高度情况复杂多变的建筑物较多的城市区域建筑容积率,阴影长度法的适用性较差。
针对以上精度分析结论,可考虑在如何进一步改善和改进阴影面积法与阴影长度法在提取复杂建筑物容积率精度方面作深入研究。
| [1] |
Chen Jiwei, Han Xuepei. Semiautomatic Extraction of Floor Area Ratio Based on Construction Shadow in High Resolution Remote Sensing Image[J]. Geomatics and Information Science of Wuhan University, 2005, 30(7): 580-582. (陈基伟, 韩雪培. 高分辨率遥感影像建筑容积率提取方法研究[J]. 武汉大学学报·信息科学版, 2005, 30(7): 580-582. ) |
| [2] |
Han Xuepei, Xu Jiangang, Fu Xiaomao. A Study on Estimating Urban FAR Based on High-Resolution Satellite Images[J]. Remote Sensing Information, 2005(2): 24-28. (韩雪培, 徐建刚, 付小毛. 基于高分辨率遥感影像的城市建筑容积率估算方法研究:以上海市中心城区为例[J]. 遥感信息, 2005(2): 24-28. DOI:10.3969/j.issn.1000-3177.2005.02.007 ) |
| [3] |
Liu Huijun, Shen Quan, Chen Rong. Tiered FAR Management[J]. Planners, 2013(7): 74-78. (刘慧军, 沈权, 陈蓉. 城市规划管理中容积率分层确定机制探讨[J]. 规划师, 2013(7): 74-78. DOI:10.3969/j.issn.1006-0022.2013.07.013 ) |
| [4] |
Gonzalez-Aguilera D, Crespo-Matellan E, Hernandez-Lopez D, et al. Automated Urban Analysis Based on LiDAR-Derived Building Models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(3): 1844-1851. DOI:10.1109/TGRS.2012.2205931 |
| [5] |
Kajimoto M, Susaki J. Urban Density Estimation from Polarimetric SAR Images Based on a POA Correction Method[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(3): 1418-1429. DOI:10.1109/JSTARS.2013.2255584 |
| [6] |
Wang Huiqing, Sha Yuejin, Wang Qing, et al. Plot Ratio Survey Technology Based on Digital Close-Range Photogrammetry[J]. Science of Surveying and Mapping, 2010, 35(6): 126-128. (王慧青, 沙月进, 王庆, 等. 数字近景摄影测量建筑容积率调查技术研究[J]. 测绘科学, 2010, 35(6): 126-128. ) |
| [7] |
Zhao Cuixiao, Chen Xi, Yang Liao, et al. Extraction of Floor Area Ratio Based on DSM[J]. Science of Surveying and Mapping, 2017, 42(5): 1-9. (赵翠晓, 陈曦, 杨辽, 等. 基于DSM的建筑物容积率提取[J]. 测绘科学, 2017, 42(5): 1-9. ) |
| [8] |
Yang Jihong, Zuo Yuqiang, Su Hang, et al. Research on Floor Area Ratio Extraction Based on Space-Borne Stereo Pair[J]. Journal of Henan Polytechnic University (Natural Science), 2018, 37(1): 54-59. (杨冀红, 左玉强, 苏航, 等. 基于星载立体像对的容积率提取研究[J]. 河南理工大学学报(自然科学版), 2018, 37(1): 54-59. ) |
| [9] |
Liu Hui. Extraction of the Floor Area Ratio in the Central District of Fuzhou City Based on an Improves Shadow Index Model[J]. Geomatics and Information Science of Wuhan University, 2014, 39(10): 1241-1247. (刘辉. 基于改进阴影指数的福州市主城区建筑容积率提取[J]. 武汉大学学报·信息科学版, 2014, 39(10): 1241-1247. ) |
| [10] |
Li Jinye, Zhang Lei, Wu Bingfang. Study on Extracting Building Density and Floor Area Ratio Based on High Resolution Image[J]. Remote Sensing Technology and Application, 2007, 22(3): 309-313. (李锦业, 张磊, 吴炳方, 等. 基于高分辨率遥感影像的城市建筑密度和容积率提取方法研究[J]. 遥感技术与应用, 2007, 22(3): 309-313. DOI:10.3969/j.issn.1004-0323.2007.03.002 ) |
| [11] |
Huo Shaofeng, Gu Xingfa, Zhan Yulin, et al. Extracting Building Plot Ratio with Shadow of ZY-3 Image[J]. Geomatics and Information Science of Wuhan University, 2018, 43(3): 444-450. (霍少峰, 顾行发, 占玉林, 等. 利用资源三号卫星影像阴影提取建筑容积率[J]. 武汉大学学报·信息科学版, 2018, 43(3): 444-450. ) |
| [12] |
Tong Xudong. Development of China High-Resolution Earth Observation System[J]. Journal of Remote Sensing, 2016, 20(5): 775-780. (童旭东. 中国高分辨率对地观测系统重大专项建设进展[J]. 遥感学报, 2016, 20(5): 775-780. ) |
| [13] |
Tao Jianbin. Research on Applications of Bayesian Network Model in the Classification of Remote Sensing Images[D]. Wuhan: Wuhan University, 2010 (陶建斌.贝叶斯网络模型在遥感影像分类中的应用方法研究[D].武汉: 武汉大学, 2010)
|
| [14] |
Li Hang. Methods of Statistical Learning[M]. Beijing: Tsinghua University Press, 2012. (李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012. )
|
| [15] |
Adeline K, Chen M, Briottet X, et al. Shadow Detection in Very High Spatial Resolution Aerial Images: A Comparative Study[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 80: 21-38. DOI:10.1016/j.isprsjprs.2013.02.003 |
| [16] |
Zhao Yingshi. Remote Sensing Application Analysis Principals and Methods[M]. 2nd ed. Beijing: Science Press, 2013: 174-175. (赵英时. 遥感应用分析原理与方法[M]. 第2版. 北京: 科学出版社, 2013: 174-175. )
|
| [17] |
Li M, Stein A, Bijker W. Urban Land Use Extraction from Very High Resolution Remote Sensing Imagery Using a Bayesian Network[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 122: 192-205. DOI:10.1016/j.isprsjprs.2016.10.007 |
| [18] |
Li Linman. Research on the Allocation of Sample Size Under Stratified Sampling[J]. Statistics and Decision, 2015(19): 18-20. (李林蔓. 分层抽样下样本量的分配方法研究[J]. 统计与决策, 2015(19): 18-20. ) |
| [19] |
Shao Zhiqiang. Method for Determining Sample Size in Sample Survey[J]. Statistics and Decision, 2012(22): 12-14. (邵志强. 抽样调查中样本容量的确定方法[J]. 统计与决策, 2012(22): 12-14. ) |
| [20] |
Ministry of Housing and Urban-Rural Development of the Peoples Republic of China. GB50096-2011 Residential Design Specification[S]. Beijing: China Architecture & Building Press, 2011 (中华人民共和国住房和城乡建设部. GB50096-2011住宅设计规范[S].北京: 中国建筑工业出版社, 2011)
|
 2019, Vol. 44
2019, Vol. 44



