文章信息
- 金淑英, 胡芬, 王密, 潘俊
- JIN Shuying, HU Fen, WANG Mi, PAN Jun
- 一种TDICCD推扫影像的坐标反变换方法
- A Novel Coordinate Inverse Transform Method for TDI CCD Pushbroom Images
- 武汉大学学报·信息科学版, 2016, 41(5): 590-597
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 590-597
- http://dx.doi.org/10.13203/j.whugis20140211
-
文章历史
- 收稿日期: 2015-02-09

2. 国家测绘地理信息局卫星测绘应用中心, 北京 , 101300
2. Satellite Surveying and Mapping Application Center, National Administration of Surveying, Mapping and Geoinformation, Beijing 101300, China
时间延迟积分电荷耦合器件(time delay integration charge coupled devices,TDI CCD)能在运动中利用多级光敏元件对同一目标进行多次积分,通过把各级弱信号进行叠加得到增强的信号,提高系统的信噪比[1]。TDI CCD器件的行积分时间在推扫成像过程中可实时调整,这较好地补偿了像移运动,使得TDI CCD推扫影像获得较高的清晰度[2]。基于这两方面的原因,TDI CCD已成为当前国内外高分辨率光学卫星影像获取的主要传感器。
坐标反变换是根据已知的物方坐标求其像方坐标的过程,是线阵推扫式影像几何处理的重要计算环节[3, 4, 5]。目前,常用的坐标反变换方法有两种,一种是基于共线方程模型的迭代式反变换,另一种则是基于有理多项式模型(RFM)的直接反变换。前者适用于行积分时间固定不变的传统CCD线阵推扫影像,其中以SPOT5卫星的高分辨率影像为典型代表,数据方为用户提供了构建共线方程模型的参数值,此外还提供一个三次多项式模型用于计算像点坐标的迭代初值;相对于前者,后者计算过程简单直接,普遍应用于IKONOS、GeoEye、WorldView等高分辨率商业卫星影像[6, 7, 8],由于数据方不提供原始影像和传感器参数信息,用户只能基于RFM在传感器校正级别图像的基础上做进一步的几何处理。然而,对于国产高分辨率光学卫星获取的原始TDI CCD推扫影像,由于行积分时间跳变,在采用有理多项式模型等通用成像几何模型替代其严格的共线方程模型时,系数拟合精度不理想,难以满足实际应用要求,因而直接采用现有的坐标反变换方法是不可行的。对此,本文提出了一种基于虚拟扫描行的TDI CCD推扫影像坐标反变换方法,实现了从物方坐标到像方坐标的快速高精度计算,巧妙地解决了该类星载传感器原始影像坐标反变换的效率和精度问题。目前,该方法已成功应用于多颗国产高分辨率光学卫星的地面预处理系统。
1 线阵推扫影像坐标反变换的常规方法线阵推扫影像坐标反变换的实现方法主要有两种[9, 10],一种是基于共线方程模型的迭代式反变换,另一种是基于有理多项式模型的直接反变换。
基于共线方程模型的迭代式坐标反变换[6]流程如图 1所示。其中,三次多项式等价于分母恒为1的有理多项式,其系数也是基于原始影像的共线方程模型计算得到的虚拟立体格网控制点通过最小二乘拟合得到的。在迭代式坐标反变换过程中,三次多项式被用于计算像方坐标的概略值。为了使得基于共线方程模型的迭代式坐标反变换能快速收敛到较高精度的像方坐标,要求三次多项式能计算出精度较高的像方坐标概略值。然而,由于行积分时间发生跳变,TDI CCD推扫影像的共线方程模型不够光滑,使得三次多项式模型的拟合精度不够,最终导致迭代次数较多、计算效率较低,甚至出现迭代不收敛的情况。
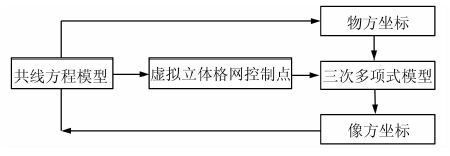
|
| 图 1 基于共线方程模型的迭代式坐标反变换 Fig. 1 Iterative Coordinate Inverse Transform Based on the Collinearity Equations |
基于有理多项式模型的坐标反变换如图 2所示,该方法需要有高精度的与共线方程模型等价的有理多项式模型,其中,有理多项式模型系数是基于共线方程模型计算得到虚拟立体格网控制点,通过最小二乘法拟合得到[11, 12]。研究发现,若线阵推扫式影像的共线方程模型不够光滑,会影响RFM系数的拟合精度。例如,若行积分时间发生跳变,在对TDI CCD推扫影像拟合RFM时,沿轨方向上的拟合误差就会变大。此外,在对SPOT5影像的共线方程模型拟合RFM时,如果不对探元指向角的取值进行多项式拟合处理,CCD方向上的拟合误差就会变大。这些都表明,共线方程模型的光滑性对其RFM的拟合精度有直接影响。

|
| 图 2 基于有理多项式模型的直接坐标反变换 Fig. 2 Direct Coordinate Inverse Transform Based on RFM |
上述两种坐标反变换方法的精度和效率都与地形无关的多项式模型有密切关系,而地形无关的多项式模型的拟合精度与原始影像共线方程模型的光滑性密切相关,这取决于原始影像是否存在行积分时间跳变。因此,对于行积分时间跳变的TDI CCD线阵推扫影像,需要寻求更为可行的坐标反变换方法。
2 基于虚拟扫描行的TDI CCD线阵推扫影像坐标反变换方法从数学微积分可知,连续且可导的函数对应的几何图形是光滑的。有理多项式、三次多项式和共线方程模型都可以看作是物方坐标关于像方坐标的函数,其中有理多项式和三次多项式是连续可导的函数。从函数拟合的角度,为使得有理多项式或三次多项式能高精度地拟合共线方程模型,共线方程模型本身也应当是一个连续可导的函数。
就TDI CCD线阵推扫影像共线方程模型的光滑性而言,一方面,共线方程模型关于成像时刻是连续可导的函数;另一方面,成像时刻关于影像行号是连续却不一定可导的函数。因此,TDI CCD线阵推扫影像的共线方程模型是否光滑,取决于成像时刻关于影像行号的函数是否可导。
基于以上分析,本文提出虚拟扫描行的概念,构建固定行积分时间的虚拟影像,使得成像时刻关于影像行号的函数连续可导;然后以成像时刻为桥梁,建立虚拟影像与原始影像的扫描行对应关系;在此基础上借助虚拟影像的共线方程模型或有理多项式模型,实现TDI CCD推扫影像坐标反变换的快速高精度计算。
2.1 虚拟扫描行TDI CCD推扫影像上每条扫描行的曝光时间也称为行积分时间。为了描述星载TDI CCD相机获取影像时的行积分时间跳变特点,本文以ZY-1 02C卫星的HR1相机为例。在记录开机时刻之后,相机将每隔一段时间记录一次行积分时间和影像行号,通过简单统计,可得到行积分时间保持不变的各个时间段内的影像行数。
假设开机时刻为0,l表示原始影像扫描行,在第l条扫描行之前共有n个时间段,每个时间段内的行积分时间固定不变,同时假设第k(k=0,1,2,…,n)个时间段的行积分时间为Δk,影像行数为L(k),则基于式(1)可计算出第l行对应的成像时刻t(l)[13, 14]:
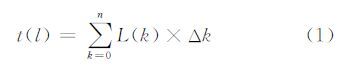
其中,行号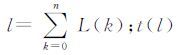 为第l行对应的成像时刻。
为第l行对应的成像时刻。
式(1)表明,行积分时间跳变情况下,Δk不全相等,成像时刻t(l)关于行号l的函数是分段线性函数,是连续不可导的。
假设虚拟影像是由行积分时间固定不变的虚拟扫描行组成的影像,与原始影像具有相同的成像总时间和影像覆盖范围,且共用一套轨道姿态及传感器参数。若虚拟影像与原始影像行数相同,由式(2)可确定虚拟扫描行行积分时间Δv:

式中,Ttotal_time为原始影像的成像总时间;Ltotal_line为原始影像行数。
由于改变的只是影像的扫描行积分时间,虚拟影像等价于对原始影像进行沿轨道方向的一维重采样。因此,对于同一物点,在这两幅影像上的同名像点列号相同,且成像时刻保持不变,改变的只是同名像点所在的扫描行计数。以成像时刻为桥梁便可建立原始扫描行与虚拟扫描行的严格对应关系。
2.2 建立原始扫描行与虚拟扫描行的对应关系如图 3所示,假设l′和l分别表示同名扫描行在虚拟影像和原始影像上的扫描行,两者可通过成像时刻实现换算。
一方面,基于式(2)计算得到的固定行积分时间Δv,虚拟影像的第l′条扫描行与其成像时刻t(l′)之间存在线性关系,如式(3)所示。
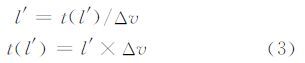
另一方面,对于同名扫描行满足t(l)=t(l′)。于是,根据星上下传的辅助数据和式(1)可确定该成像时刻所对应的原始影像扫描行l。

|
| 图 3 虚拟扫描行与原始扫描行之间的关系 Fig. 3 Relationship Between Virtual Image Scanline and Original Image Scanline |
由前述可知,无论采用迭代式坐标反变换还是采用直接坐标反变换,地形无关的多项式模型是必不可少的。根据虚拟影像的共线方程模型计算物方虚拟立体格网控制点,然后通过最小二乘平差解算得到与地形无关的多项式模型系数。
物方虚拟立体格网控制点坐标的计算过程如下。
假设虚拟影像像点p(s,l′)对应的物方坐标为WGS84地心直角坐标(X,Y,Z),则满足下列共线方程:
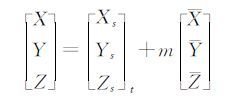
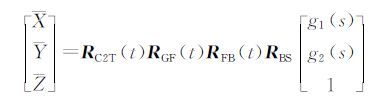
式中,s为探元号;g1(s)、g2(s)为通过内方位元素模型求得的光线矢量在相机坐标系中的两个视角的正切值;t为l′对应的成像时刻;[Xs Ys Zs]T为t时刻卫星质心位置矢量; RC2T(t)、RGF(t)、RFB(t)、RBS分别为t时刻下从J2000坐标系到WGS84地心直角坐标系的旋转矩阵、从轨道坐标系到J2000坐标系的旋转矩阵、从卫星本体坐标系到轨道坐标系的旋转矩阵以及从相机坐标系到卫星本体坐标系的旋转矩阵。
将共线方程变为如下形式:
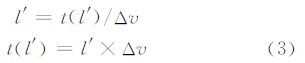
求解比例系数m的过程如下。
假设WGS84椭球的长半轴为a,短半轴为b,物点P的椭球高为H,则从虚拟影像上的点p(s,l′)出发的光线与长半轴为A=a+H、短半轴为B=b+H的椭球面相交得到物点P的物方坐标(X,Y,Z)满足下列椭球面方程:
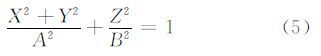
将式(4)代入式(5),化简后得到关于m的一元二次方程: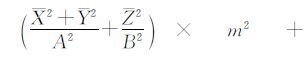
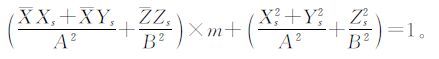
解出m,代入式(4)解出P的物方坐标(X,Y,Z),可将地心直角坐标(X,Y,Z)转换为地理坐标(B,L)。
需要特别说明的是,对于虚拟影像的虚拟立体格网点,高程H是定义在WGS84椭球面上的虚拟高程面,不是从真实DEM内插的高程。实际计算时,需要对虚拟影像划分规则格网,对物方空间划分多个高程面,计算每个格网点与各个高程面的交点坐标。为了避免过度参数化造成的奇异矩阵求逆问题,多项式模型系数的求解可以采用谱修正迭代法进行求解[15]。
2.4 基于虚拟扫描行的原始影像坐标反变换基于虚拟扫描行的原始影像坐标反变换有直接法和迭代法两种。
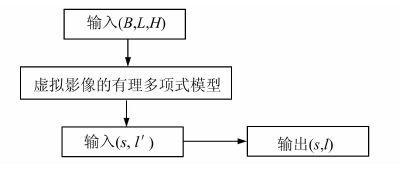
直接法的处理流程如图 4所示,其中,(B,L,H)是物方坐标,(s,l′)是对应的虚拟影像坐标,(s,l′)是对应的原始影像坐标。
|
| 图 4 基于虚拟影像有理多项式模型的直接坐标反变换 Fig. 4 Direct Coordinate Inverse Transform Based on RFM of Virtual Image |
在求解了虚拟影像对应的地形无关的有理多项式模型系数后,可以分两步骤实现从物方坐标到原始影像坐标的直接反变换:(1)根据虚拟影像的与地形无关的有理多项式模型从物方坐标(B,L,H)直接计算虚拟影像坐标(s,l′);(2)根据虚拟影像坐标(s,l′)计算原始影像坐标(s,l),即实现虚拟扫描行到原始扫描行的行号转换,具体实现过程参见§3.2。
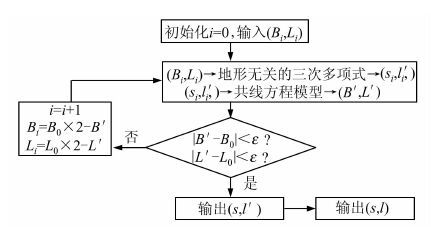
迭代法的处理流程如图 5所示,(Bi,Li)为第i次迭代的物方坐标输入值,其中,(B0,L0)为已知的物方坐标,H0为已知的高程值,(si,l′i)为第i次虚拟影像坐标计算结果,(B′,L′)为根据第i次的虚拟影像坐标计算得到的新物方坐标,(s,l′)和(s,l)为最终输出的虚拟影像坐标和原始影像坐标。
|
| 图 5 基于虚拟影像共线方程模型的迭代式坐标反变换 Fig. 5 Iterative Coordinate Inverse Transform Based on the Collinearity Equations of Virtual Image |
在求解了虚拟影像对应的与地形无关的三次多项式模型系数后,可以分两步骤实现从物方坐标到原始影像坐标的迭代式反变换:
1) 由物方坐标(B0,L0,H0)迭代计算虚拟影像像点坐标(s,l′)。根据虚拟影像对应的与地形无关的三次多项式,估算物方坐标(B0,L0,H0)在虚拟影像上像点坐标的概略值(si,l′i);根据虚拟影像对应的共线方程模型,计算新的物方坐标值(B′,L′);将新的物方坐标(B′,L′)与已知的物方坐标(B0,L0)进行对比,若差值小于给定的阈值,则输出当前计算的像点坐标(si,l′i)作为最终结果;否则,根据新的物方坐标(B′,L′)和已知的物方坐标(B0,L0)计算新的物方坐标输入值(Bi,Li),继续迭代[6]。
2) 由虚拟影像像点坐标(s,l′)计算原始影像像点坐标(s,l)。 根据§3.2节,原始影像与虚拟影像之间只有扫描行方向上的差异(一维),而原始影像扫描行l与虚拟影像扫描行l′之间通过成像时刻t建立了一一对应关系,所以很容易根据虚拟影像扫描行l′求得成像时刻t,再求得原始影像扫描行l。
3 实验与分析 3.1 实验数据本文选取ZY-1 02C卫星HR1相机获取的原始TDI CCD推扫影像作为实验数据,成像日期为2012年1月23日。从中截取了大约20万行,辅助数据中的原始影像行号、成像时刻及行积分时间参数如表 1所示。实验时从中截取8个小段,分为两组,其中奇数组包含行积分时间跳变,偶数组不包含行积分时间跳变,如表 2所示。每组含有4个数据,长度分别为2万行、4万行、6万行和8万行。
| 原始影像行号 | 成像时刻 | 行积分时间/μs | 原始影像行号 | 成像时刻 | 行积分时间/μs |
| 162 957 | 0 | 349.333 333 | 272 979 | 38.474 37 | 349.333 333 |
| 172 897 | 3.472 374 | 349.333 333 | 283 077 | 42.001 93 | 349.333 333 |
| 182 995 | 6.999 942 | 349.333 333 | 293 017 | 45.474 31 | 349.333 333 |
| 192 919 | 10.473 34 | 350.000 000 | 303 115 | 49.001 88 | 349.333 333 |
| 202 998 | 14.000 99 | 350.000 000 | 313 055 | 52.474 25 | 349.333 333 |
| 212 920 | 17.473 69 | 350.000 000 | 323 158 | 56.003 56 | 349.333 333 |
| 223 017 | 21.000 91 | 349.333 333 | 333 094 | 59.474 54 | 349.333 333 |
| 232 957 | 24.473 28 | 349.333 333 | 343 192 | 63.002 11 | 349.333 333 |
| 243 053 | 28.006 88 | 350.000 000 | 353 132 | 66.474 48 | 349.333 333 |
| 252 974 | 31.479 23 | 350.000 000 | 363 230 | 70.002 05 | 349.333 333 |
| 263 053 | 35.006 88 | 350.000 000 |
| 测试数据 | 起始行 | 行数 | 行积分时间有无跳变 |
| 1 | 230 000 | 20 000 | 有 |
| 2 | 300 000 | 20 000 | 无 |
| 3 | 170 000 | 40 000 | 有 |
| 4 | 300 000 | 40 000 | 无 |
| 5 | 190 000 | 60 000 | 有 |
| 6 | 300 000 | 60 000 | 无 |
| 7 | 200 000 | 80 000 | 有 |
| 8 | 280 000 | 80 000 | 无 |
为验证“行积分时间跳变使得共线方程模型不光滑,导致地形无关的多项式函数拟合精度下降”的理论,以及本文提出的基于虚拟扫描行的TDI CCD推扫影像坐标反变换法的精度,并与常规方法即基于原始影像的坐标反变换法进行对比,本文的实验分为以下几个步骤。
1) 首先,对原始TDI CCD推扫影像和虚拟影像(并不存在,也无需生成,其影像大小与原始影像相同)分别建立共线方程模型;对两个影像分别划分规则格网和多个高程面,通过基于共线方程模型的坐标正变换,计算出一批虚拟立体格网控制点和检查点。其中,控制点格网分5个高程面,每个高程面上的格网起点从影像左上角(0,0)开始,格网大小为256×256像素;检查点格网分4个高程面,每个高程面上的格网起点偏离左上角(128,128)像素,格网大小256×256像素。
2) 基于虚拟立体格网控制点,解算可替代原始影像的共线方程模型的有理多项式M1系数和三次多项式M2系数,以及可替代虚拟影像的共线方程模型的有理多项式M3系数和三次多项式M4系数,其中有理多项式系数拟合时,采用谱修正迭代法避免奇异矩阵求逆,最后统计上述4个替代模型的拟合误差。
3) 分别采用上述4个替代模型对虚拟立体格网检查点进行坐标反变换(方法1对应于M1,方法2对应于M2,方法3对应于M3,方法4对应于M4),最后统计检查点的像方坐标误差。
3.3 实验结果与分析实验结果如表 3~6所示。表 3和表 4是用8组数据的虚拟立体格网控制点拟合4个模型的中误差和最大误差。表 5和表 6是用8组数据的虚拟立体格网检查点进行坐标反变换统计的中误差和最大误差。从表 3~6可以得出以下实验结果:
| 数据 | 方法1 | 方法2 | 方法3 | 方法4 | ||||
| x方向 | y方向 | x方向 | y方向 | x方向 | y方向 | x方向 | y方向 | |
| 1 | 0.000 120 | 0.211 654 | 0.000 121 | 0.451 544 | 0.000 120 | 0.000 134 | 0.000 121 | 0.000 235 |
| 2 | 0.000 122 | 0.000 141 | 0.000 123 | 0.000 408 | 0.000 122 | 0.000 141 | 0.000 123 | 0.000 408 |
| 3 | 0.000 120 | 0.729 037 | 0.000 129 | 0.868 465 | 0.000 120 | 0.000 134 | 0.000 130 | 0.001 157 |
| 4 | 0.000 126 | 0.000 334 | 0.000 192 | 0.003 506 | 0.000 126 | 0.000 334 | 0.000 192 | 0.003 506 |
| 5 | 0.000 120 | 1.017 999 | 0.000 176 | 2.480 167 | 0.000 120 | 0.000 135 | 0.000 176 | 0.002 043 |
| 6 | 0.000 159 | 0.001 003 | 0.000 400 | 0.011 036 | 0.000 159 | 0.001 003 | 0.000 400 | 0.011 036 |
| 7 | 0.000 120 | 1.183 678 | 0.000 336 | 5.313 222 | 0.000 120 | 0.000 134 | 0.000 336 | 0.000 703 |
| 8 | 0.000 124 | 0.000 278 | 0.000 294 | 0.006 306 | 0.000 124 | 0.000 278 | 0.000 294 | 0.006 306 |
| 数据 | 方法1 | 方法2 | 方法3 | 方法4 | ||||
| x方向 | y方向 | x方向 | y方向 | x方向 | y方向 | x方向 | y方向 | |
| 1 | 0.000 289 | 0.750 552 | 0.000 315 | 1.257 715 | 0.000 294 | 0.000 286 | 0.000 322 | 0.001 037 |
| 2 | 0.000 294 | 0.000 381 | 0.000 306 | 0.001 936 | 0.000 294 | 0.000 381 | 0.000 306 | 0.001 936 |
| 3 | 0.000 296 | 2.335 159 | 0.000 513 | 2.537 412 | 0.000 301 | 0.000 298 | 0.000 577 | 0.005 011 |
| 4 | 0.000 370 | 0.001 314 | 0.000 813 | 0.017 349 | 0.000 370 | 0.001 314 | 0.000 813 | 0.017 349 |
| 5 | 0.000 291 | 3.853 396 | 0.000 979 | 6.223 206 | 0.000 287 | 0.000 338 | 0.000 949 | 0.008 961 |
| 6 | 0.000 567 | 0.003 642 | 0.001 924 | 0.071 586 | 0.000 567 | 0.003 642 | 0.001 924 | 0.071 586 |
| 7 | 0.000 295 | 4.092 933 | 0.002 152 | 13.162 20 | 0.000 298 | 0.000 308 | 0.002 190 | 0.003 550 |
| 8 | 0.000 353 | 0.001 535 | 0.001 553 | 0.038 853 | 0.000 353 | 0.001 535 | 0.001 553 | 0.038 853 |
| 数据 | 方法1 | 方法2 | 方法3 | 方法4 | ||||
| x方向 | y方向 | x方向 | y方向 | x方向 | y方向 | x方向 | y方向 | |
| 1 | 0.000 120 | 0.212 642 | 0.000 121 | 0.442 671 | 0.000 121 | 0.000 135 | 0.000 122 | 0.000 212 |
| 2 | 0.000 121 | 0.000 141 | 0.000 122 | 0.000 353 | 0.000 121 | 0.000 141 | 0.000 122 | 0.000 353 |
| 3 | 0.000 120 | 0.724 599 | 0.000 128 | 0.861 416 | 0.000 121 | 0.000 134 | 0.000 129 | 0.000 999 |
| 4 | 0.000 126 | 0.000 315 | 0.000 185 | 0.003 365 | 0.000 126 | 0.000 315 | 0.000 185 | 0.003 365 |
| 5 | 0.000 120 | 0.999 470 | 0.000 171 | 2.469 359 | 0.000 119 | 0.000 136 | 0.000 170 | 0.001 783 |
| 6 | 0.000 160 | 0.000 969 | 0.000 389 | 0.010 247 | 0.000 160 | 0.000 969 | 0.000 389 | 0.010 247 |
| 7 | 0.000 120 | 1.160 452 | 0.000 321 | 5.291 627 | 0.000 121 | 0.000 136 | 0.000 325 | 0.000 624 |
| 8 | 0.000 126 | 0.000 275 | 0.000 277 | 0.006 019 | 0.000 126 | 0.000 275 | 0.000 277 | 0.006 019 |
| 数据 | 方法1 | 方法2 | 方法3 | 方法4 | ||||
| x方向 | y方向 | x方向 | y方向 | x方向 | y方向 | x方向 | y方向 | |
| 1 | 0.000 285 | 0.828 922 | 0.000 309 | 1.330 628 | 0.000 306 | 0.000 289 | 0.000 346 | 0.000 851 |
| 2 | 0.000 319 | 0.000 373 | 0.000 325 | 0.001 578 | 0.000 319 | 0.000 373 | 0.000 325 0 | 0.001 578 |
| 3 | 0.000 291 | 2.314 962 | 0.000 367 | 2.514 761 | 0.000 295 | 0.000 294 | 0.000 444 0 | 0.004 412 |
| 4 | 0.000 363 | 0.001 158 | 0.000 792 | 0.016 630 | 0.000 363 | 0.001 158 | 0.000 792 0 | 0.016 630 |
| 5 | 0.000 290 | 3.297 445 | 0.000 793 | 5.973 851 | 0.000 303 | 0.000 321 | 0.000 798 0 | 0.008 150 |
| 6 | 0.000 564 | 0.003 184 | 0.001 808 | 0.061 472 | 0.000 564 | 0.003 184 | 0.001 808 0 | 0.061 472 |
| 7 | 0.000 295 | 3.490 773 | 0.001 791 | 12.859 64 | 0.000 295 | 0.000 294 | 0.001 842 0 | 0.003 202 |
| 8 | 0.000 352 | 0.001 441 | 0.001 357 | 0.036 975 | 0.000 352 | 0.001 441 | 0.001 357 0 | 0.036 975 |
1) 对比4种方法,方法1和方法2的误差比较大,方法3和方法4较优。因此,本文基于虚拟扫描行的方法优于常规基于原始影像的方法。另对比还发现,方法1的误差小于方法2的误差,方法3的误差小于方法4的误差。因此,有理多项式模型比三次多项式模型用于替代共线方程模型的精度更高。
2) 对比方法1和方法2中的奇数组数据和偶数组数据,偶数组数据的精度较优。分析原因,这是因为奇数组数据存在行积分时间跳变,原始影像的共线方程模型不够平滑导致的。这证明了行积分时间跳变使得共线方程模型的光滑性下降,也可以解释共线方程模型的光滑性与多项式模型精度之间存在的关系。
3) 对比方法1和方法2中的奇数组数据在两个方向上的误差,x方向(即垂轨方向,CCD方向)误差较小,而y方向(即沿轨方向,卫星飞行方向)误差较大。分析原因,这是因为原始影像的奇数组数据存在行积分时间跳变,其共线方程模型关于探元的函数是连续且可导的,而其共线方程模型关于原始影像行号的函数是连续却不可导的。这充分证明了共线方程模型的光滑性、函数的可导性和替代模型的精度是保持高度一致的。
4) 方法1和方法2中,对比4个奇数组数据在y方向上的误差,发现原始影像的行数越多,y方向上的误差也越大。分析原因,成像时刻关于原始影像行号是分段线性函数,这是因为原始影像的行数越多,成像的时间越长,分段数越多,共线方程模型复杂度越高,更难以用多项式模型来拟合,最终导致多项式模型的精度下降。
以上实验结果与本文预期是非常符合一致的。因此,本文方法实现了行积分时间跳变情况下从物方坐标高精度地反算像方坐标。
同时,实验结果表明,共线方程模型本身的光滑性决定了替代模型拟合的精度。因此,当替代模型拟合误差较大时,可以从共线方程模型本身去找原因。例如,沿轨方向上的误差可能来源于成像时刻关于影像扫描行的函数不光滑,垂轨方向上的误差则可能来源于视线方向关于探元的函数不够光滑。
另外,由于有理多项式函数具有过度参数化、奇异矩阵求逆、模型精度受控制点分布和数量的影响等多种不确定性,对于成像时间较短的具有行积分时间跳变的TDI CCD推扫影像,常规的方法即基于原始影像的有理多项式模型也可能出现拟合精度较高的情况。
4 结 语坐标反变换是线阵推扫式影像几何处理的重要计算环节。对于存在行积分时间跳变的TDI CCD推扫影像,直接采用常规的坐标反变换方法可行性较差,难以满足精度要求。本文提出了一种基于虚拟扫描行的TDI CCD推扫影像坐标反变换方法。该方法假定由行积分时间相等的虚拟扫描行构成虚拟影像,基于虚拟影像的共线方程模型或高精度有理多项式模型,反算物点在虚拟影像上的像点坐标;基于虚拟影像与TDI CCD推扫影像的扫描行映射关系,进而得到该物点在TDI CCD推扫影像上的像点坐标。基于该方法的计算过程并不需要生成实际的虚拟影像,巧妙地解决了TDI CCD推扫影像坐标反变换的效率和精度问题。利国产资源卫星进行实验验证了此方法的正确性和可行性。
| [1] | Xue Xucheng, Shi Junxia, Lü Hengyi. Optimal Set of TDI CCD Integration Stages and Gains of Space Remote Sensing Cameras[J]. Optics Precision Engineering, 2011, 19(4):857-863(薛旭成,石俊霞,吕恒毅.空间遥感相机TDICCD积分级数和增益的优化设置[J].光学精密工程, 2011, 19(4):857-863) |
| [2] | Yan Dejie, Xu Shuyan, Han Chengshan. Effect of Aerocraft Attitude on Image Motion Compensation of Space Camera[J]. Optics Precision Engineering, 2008, 16(11):2199-2203(闫德杰,徐抒岩,韩诚山.飞行器姿态对空间相机像移补偿的影响[J]. 光学精密工程, 2008, 16(11):2199-2203) |
| [3] | Wang Mi, Hu Fen, Wang Haitao. A Fast Algorithm for Back Projection Calculation of Linear Array Pushbroom Imageries Based on Object-space Geometric Constraints[J]. Acta Geodaetica et Cartographica Sinica,2008,37(3):384-390(王密,胡芬,王海涛.一种基于物方几何约束的线阵推扫式影像坐标反投影计算的快速算法[J]. 测绘学报, 2008, 37(3):384-390) |
| [4] | Zhao Shuangming, Li Deren. Geometric Pre-processing of ADS40 Image[J]. Geomatics and Information Science of Wuhan University,2006, 31(4):308-311(赵双明,李德仁.ADS40影像几何预处理[J]. 武汉大学学报·信息科学版, 2006, 31(4):308-311) |
| [5] | Wang Mi, Hu Fen, Jin Shuying. Object-Space Back Project Coordinates Calculation Algorithm for ADS40 Images[J]. Geomatics and Information Science of Wuhan University, 2009, 34(2):187-190(王密,胡芬,金淑英.一种ADS40影像物方反投影坐标计算的快速算法[J]. 武汉大学学报·信息科学版,2009,34(2):187-190) |
| [6] | Aguilar M A, del Saldana M M, Aguilar F J. Assessing Geometric Accuracy of the Orthorectification Process from GeoEye-1 and WorldView-2 Panchromatic Images[J]. International Journal of Applied Earth Observation and Geoinformation 2013, 21(1), 427-435 |
| [7] | Poli D. Review of Developments in Geometric Modelling for High Resolution Satellite Pushbroom Sensors[J]. The Photogrammetric Record,2012,27(137):58-73 |
| [8] | Poli D. Modelling of Spaceborne Linear Array Sensors[J]. Photogrammetric Engineering & Remote Sensing,2007,73(2):187-196 |
| [9] | Spotimaging. SPOT Satellite Geometry Handbook[EB/OL]. http://www.spotimage.fr/, 2013 |
| [10] | Zhang Li, Zhang Jixian, Chen Xiangyang, et al. Block-Adjustment With SPOT-5 Imagery and Sparse GCPs Based on RFM[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4):303-311(张力,张继贤,陈向阳,等.基于有理多项式模型RFM的稀少控制SPOT-5卫星影像区域网平差[J]. 测绘学报, 2009, 38(4):303-311) |
| [11] | Yuan Xiuxiao, Lin Xianyong. A Method for Solving Rational Polynomial Coefficients Based on Ridge Estimation[J]. Geomatics and Information Science of Wuhan University,2008, 33(11):1130-1133(袁修孝,林先勇.基于岭估计的有理多项式参数求解方法[J]. 武汉大学学报·信息科学版, 2008, 33(11):1130-1133) |
| [12] | Yuan Xiuxiao, Cao Jinshan. An Optimized Method for Selecting Rational Polynomial Coeffients Based on Multicollinearity Analysis[J]. Geomatics and Information Science of Wuhan University,2011, 36(6):665-669(袁修孝,曹金山.一种基于复共线性分析的RPC参数优选法[J]. 武汉大学学报·信息科学版,2011, 36(6):665-669) |
| [13] | Hu Fen. Research on Inner FOV Stitching Theories and Algorithms for Sub-images of Three Non-collinear TDI CCD Chips[D]. Wuhan:Wuhan University,2010(胡芬.三片非共线TDI CCD成像数据内视场拼接理论与算法研究[D]. 武汉:武汉大学, 2010) |
| [14] | Pan Jun, Hu Fen, Wang Mi, et al. Inner FOV Stitching of ZY-102C HR Camera Based on Virtual CCD Line[J]. Geomatics and Information Science of Wuhan University,2015,40(4):436-443(潘俊,胡芬,王密,金淑英,基于虚拟线阵的ZY-102C卫星HR相机内视场拼接方法[J]. 武汉大学学报·信息科学版,2015,40(4):436-443) |
| [15] | Liu Bin, Gong Jianya, Jiang Wanshou, et al. Improvement of the Iteration by Correcting Characteristic Value Based on Ridge Estimation and Its Application in RPC Calculation[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4):399-402(刘斌,龚健雅,江万寿,等.基于岭参数的谱修正迭代法及其在有理多项式参数求解中的应用[J]. 武汉大学学报·信息科学版, 2012,37(4):399-402) |
 2016, Vol. 41
2016, Vol. 41


