文章信息
- 刘斌, 郭际明, 史俊波, 吴迪军
- LIU Bin, GUO Jiming, SHI Junbo, WU Dijun
- 利用EGM2008模型与地形改正进行GPS高程拟合
- A GPS Height Fitting Method Based on the EGM2008 Model and Terrain Correction
- 武汉大学学报·信息科学版, 2016, 41(4): 554-558
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 554-558
- http://dx.doi.org/10.13203/j.whugis20140125
-
文章历史
- 收稿日期: 2014-11-06

2. 中铁大桥勘测设计院集团有限公司, 湖北 武汉, 430050
2. China Railway Major Bridge Reconnaissance and Design Institute CO. LTD., Wuhan 430050, China
将GPS高程测量测得的大地高转换为工程上应用的正常高,关键在于高程异常的求解[1, 2]。由美国地理空间情报局(National Geospatial Intelligence Agency,NGA)发布的空间分辨率为5′(约为9 km)的EGM2008重力场模型能够精确表达高程异常的长波项[3, 4, 5, 6]。高程异常的短波项由地形变化引起[7],在地形起伏大的地区,地形变化是影响高程异常的重要因素,而EGM2008重力场模型不能很好地解决地形变化产生的短波项的影响。在实际工程应用中求解高程异常时,常利用数值逼近方法考虑地形因素的影响[8, 9],而忽略高程异常的长波部分;或只考虑长波项的影响,不考虑地形因素的影响[10, 11, 12, 13];亦或结合EGM2008重力场模型并考虑地形影响,求解地形影响时采用重力引力位法、棱柱积分法等方法[14, 15],计算过程复杂。
利用“移去-拟合-恢复”法的思想,本文提出了一种基于EGM2008模型求解高程异常长波项,利用数字高程模型(digital elevation model,DEM)格网数据求解地形起伏变化引起的高程异常短波项,并结合二次曲面拟合法拟合残余高程异常的GPS高程拟合方法。通过港珠澳大桥的实例数据,将仅考虑地形因素的二次曲面拟合,仅结合EGM2008模型的二次曲面拟合方法与本文提出方法的GPS高程拟合精度进行比较。
1 原理与方法 1.1 原理及流程本文选择“移去-拟合-恢复”法求解高程异常[16],该方法综合利用EGM2008模型与数学拟合方法,无须实测重力数据,只须联测少量水准点,尤其是在地形起伏较大、水准联测点较少的地区,能方便地进行GPS高程拟合。根据物理大地测量学理论,高程异常ζ可以表示为[12]:
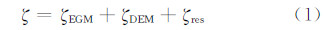
式中,ζEGM是由EGM2008模型求得的高程异常长波部分;ζDEM是地形起伏变化引起的高程异常短波部分;ζres是残余高程异常。“移去-拟合-恢复”法思路为,从已知点的ζ中移去ζEGM与ζDEM,获得ζres进行模型拟合;基于拟合模型计算待求点的ζres,再加上ζDEM与ζEGM,就可得到待求点的高程异常ζ,具体处理流程见图 1。

|
| 图 1 “移去-拟合-恢复”法求解高程异常的流程图 Fig. 1 Flowchart of the Height Anomaly Determination Based on the Remove-fit-restore Approach |
EGM2008模型是由NGA发布的全球超高阶重力场模型,它以PGM2007B为参考,综合利用GRACE卫星重力数据、全球5′×5′重力异常数据、TOPEX卫星测高数据、地形数据以及地面重力数据[17, 18]。该模型的阶次完全至2 159[19](另外球谐系数的阶扩展至2 190,次为2 159),先利用EGM2008模型求得扰动位T[20],再根据Burns公式计算地面上任一点的高程异常长波项:

式中,ρ、φ和λ分别为计算点地心向径、余纬和经度;GM为地心引力常数;a为椭球长半径;Cnm、Snm为完全规格化位系数;Pnm(sinφ)为完全规格化缔合函数;γ为计算点的正常重力值。
1.3 地形变化引起的高程异常短波项由地形起伏变化引起的高程异常变化量δ可表示为[16]:
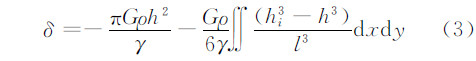
式中,G为万有引力常数;ρ为地球质量密度;hi为流动单元平均高程;h为待求点高程;γ为待求点正常重力;l为待求点到流动单元的距离;dxdy为流动单元面积。
高程异常短波项ζDEM的求解步骤如下。
1)获取所在区域的DEM数据。目前美国国家航空和宇宙航行局(The National Aeronautics and Space Administration,NASA)公开的DEM在中国境内的分辨率为3″(90 m),根据拟合区域的坐标最大值与最小值选择对应的DEM格网数据。
2)划分流动单元。
3)求解流动单元的平均高程,即单元4个格网点的平均高程,利用式(3)可以求得每一个格网点的高程异常。
4)按双线性内插法计算待求点的高程异常短波项:

式中,a、b、c、d为流动单元的4个格网点(依次为左下角、左上角、右上角、右下角);l为流动单元边长;Δx、Δy为待求点与流动单元左下角格网点的坐标差。
1.4 二次曲面拟合残余高程异常主要由模型误差、数据误差等引起,可通过数学函数对其规律性进行拟合。常用的数学函数有二次曲面函数、平面函数、反距离加权内插函数等[11, 12]。在实际工程中,大多采用二次曲面函数拟合残余高程异常[14, 15, 21],其函数表达式为:
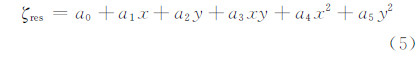
式中,ζres表示残余高程异常;x、y表示点的重心化坐标;a0、…、a5表示拟合系数。联测水准点的个数应不少于6个,使用最小二乘法进行求解。
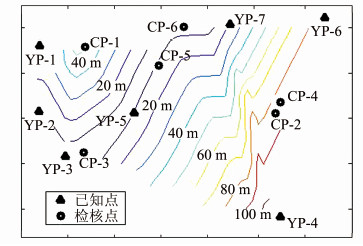
2 算例分析本文利用某跨海大桥工程项目的实测数据进行高程拟合方法分析。该工程数据点分布在长约53 km、宽约28 km的范围内。使用GPS接收机观测了39个点,并用精密水准测量方法联测了其中的13个点。将7个联测点作为已知点(高程均值33.036 7 m,高程最大值106.174 6 m,最小值1.036 4 m),6个联测点作为检核点(高程均值37.890 9 m,高程最大值89.489 3 m,最小值-0.228 6 m),点位平面分布情况见图 2。图 2显示,用于拟合模型的7个已知点基本覆盖工程范围,6个检核点均在拟合范围之内。
|
| 图 2 GPS点位分布图 Fig. 2 Site Distribution of GPS Stations |
分别使用表 1中的三种方法(分别为仅考虑地形因素的二次曲面拟合,仅结合EGM2008模型的二次曲面拟合方法与本文方法)进行GPS高程拟合。表 1中“是”/“否”表示考虑/不考虑相关影响,在考虑地形因素时,本文将流动单元划分为270 m×270 m的格网来求解由地形起伏变化引起的高程异常变化量。
| EGM2008模型 | 地形因素 | 二次曲面 | |
| 方法1 | 否 | 是 | 是 |
| 方法2 | 是 | 否 | 是 |
| 本文方法 | 是 | 是 | 是 |
对以上三种方法按式(6)、(7)进行内外符合精度的评定:

式中,STD表示内符合精度;ε为已知点的高程异常残差;n为已知点的个数;RMS表示外符合精度;Δ为检核点的高程异常残差;m为检核点的个数。内符合精度反映了利用已知点进行建模的模型质量,外符合精度反映了利用所建模型求解检核点高程异常的整体质量。
图 3和图 4分别是三种方法拟合已知点和检核点高程异常的残差比较。从图 3可以看出,7个已知点在本文提出的方法下拟合残差均最小,相对方法1和方法2均有mm级的改进精度;本文方法的高程异常残差最大值为0.26 cm,小于方法1的0.70 cm和方法2的0.72 cm,其残差均值为-0.01 cm,也小于方法1的0.13 cm和方法2的0.02 cm;本文提出方法的内符合精度为0.16 cm,优于方法1的0.43 cm和方法2的0.41 cm。实验结果表明,利用本文提出的方法能够提高建模精度。

|
| 图 3 不同方法已知点高程异常残差比较 Fig. 3 Comparison of the Height Anomaly Residuals of Known Points by Different Methods |
|
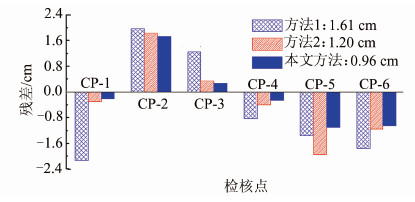
| 图 4 不同方法检核点高程异常残差比较 Fig. 4 Comparison of the Height Anomaly Residuals of Checked Points by Different Methods |
从图 4可以看出,6个检核点在本文方法中高程异常残差最小,精度较方法1和方法2均有mm级改进;本文方法的高程异常残差最大值为1.72 cm,小于方法1的1.96 cm和方法2的1.82 cm;本文方法的外符合精度达到了0.96 cm,优于方法1的1.61 cm和方法2的1.20 cm。
改变已知点与检核点的个数,用上述三种方法进行验证,其拟合效果见表 2。需要注意的是,当用1个检核点进行检核时,为防止因已知点的选择而造成拟合偏差过大,本文用交叉验证法[22]进行处理。
| 已 知点-检 核点 个数 | 8-5 | 9-4 | 10-3 | 11-2 | 12-1 | |||||
| 内符合 | 外符合 | 内符合 | 外符合 | 内符合 | 外符合 | 内符合 | 外符合 | 内符合 | 外符合 | |
| 方法1 | 0.41 | 1.95 | 0.61 | 1.63 | 0.86 | 1.47 | 0.89 | 1.33 | 0.87 | 1.66 |
| 方法2 | 0.40 | 2.26 | 0.68 | 1.83 | 0.95 | 1.35 | 0.95 | 1.32 | 0.96 | 1.96 |
| 本文方法 | 0.15 | 1.72 | 0.49 | 1.42 | 0.55 | 1.23 | 0.65 | 0.98 | 0.71 | 1.34 |
表 2显示,在改变已知点与检核点的个数后,本文提出方法的内、外符合精度较方法1、方法2均有mm级的改进;已知点与检核点的个数虽然发生变化,但本文提出方法的内符合精度均达到mm级,外符合精度均达到cm级。实验结果表明,本文提出的方法能够提高GPS高程拟合的精度。
3 结语利用“移去-拟合-恢复”的思想,本文提出了一种基于EGM2008模型,并考虑地形因素影响的二次曲面拟合GPS高程的方法。相比以往的高程异常求解方法,本文提出的方法精度较高。通过某跨海大桥工程的实测数据,比较分析了仅考虑地形因素的二次曲面拟合法、仅结合EGM2008模型的二次曲面拟合法和本文提出的基于EGM2008模型和地形改正的二次曲面拟合法的拟合效果。结果表明,本文提出的方法精度较高,其内符合精度达到0.16 cm,外符合精度达到0.96 cm,能够提高GPS高程拟合精度。此外,由于本文的研究工作是基于工程项目建设的实际地形特征完成的,提出的方法对于其他地形区域的适用性还需要进一步分析和验证。结合多种地形特征,进一步完善计算模型,提高模型的通用性是下一步研究的重点。
| [1] | Li Jiancheng. Study and Progress in Theories and Crucial Techniques of Modern Height Measurement in China[J]. Geomatics and Information Science of Wuhan University, 2007, 32(11):980-987(李建成. 我国现代高程测定关键技术若干问题的研究及进展[J]. 武汉大学学报·信息科学版, 2007, 32(11):980-987) |
| [2] | Wang Zhengtao, Li Jiancheng, Chao Dingbo. Problem on Fitting Between Marine Gravity Quasi-geoid and Local Altimetric Quasi-geoid[J]. Geomatics and Information Science of Wuhan University, 2005, 30(3):234-237(王正涛, 李建成, 晁定波. 海洋重力似大地水准面与区域测高似大地水准面的拟合问题[J]. 武汉大学学报·信息科学版, 2005, 30(3):234-237) |
| [3] | Zhang Chuanyin, Guo Chunxi, Chen Junyong, et al. EGM2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009,38(4):283-289(章传银, 郭春喜, 陈俊勇, 等. EGM2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4):283-289) |
| [4] | Lin Miao, Zhu Jianjun, Yang Jinghao, et al. Comparison of the Regional Geoid Undulations Determinated by Geopotential Models[J]. Geomatics and Information Science of Wuhan University,2009, 34(10):1194-1198(林淼, 朱建军, 杨经豪, 等. 地球重力位模型确定局部大地水准面起伏的比较研究[J]. 武汉大学学报·信息科学版, 2009, 34(10):1194-1198) |
| [5] | Shu Chanfang, Li Fei, Hao Weifeng. Evaluation of EGM2008 and Its Application Analysis over a Particular Region of China[J]. Geomatics and Information Science of Wuhan University,2011, 36(8):919-922(束蝉方, 李斐, 郝卫峰. EGM2008模型在中国某地区的检核及适用性分析[J]. 武汉大学学报·信息科学版, 2011, 36(8):919-922) |
| [6] | Rong Min, Zhou Wei, Chen Chunwang. Evaluation of Gravity Field Models EGM2008 and EGM96 Applied in Chinese Area[J]. Journal of Geodesy and Geodynamics, 2009,29(6):123-125(荣敏, 周巍, 陈春旺. 重力场模型EGM2008和EGM96在中国地区的比较与评价[J]. 大地测量与地球动力学, 2009, 29(6):123-125) |
| [7] | Luo Zhicai, Chen Yongqi, Ning Jinsheng. Effect of Terrain on the Determination of High Precise Local Gravimetric Geoid[J]. Geomatics and Information Science of Wuhan University,2003, 28(3):340-345(罗志才, 陈永奇, 宁津生. 地形对确定高精度局部大地水准面的影响[J]. 武汉大学学报·信息科学版, 2003, 28(3):340-345) |
| [8] | Niu Zhihong, Song Mengbo, Chen Jiqin. Comparative Research on GPS Height Fitting Methods Based on Neural Network[J]. Procedia Engineering, 2012, 28:696-702 |
| [9] | Erol B, Erol S. Learning-based Computing Techniques in Geoid Modeling for Precise Height Transformation[J].Computers and Geosciences, 2013, 52:95-107 |
| [10] | Xing S D, Xiang H H, Yang S Y. Transfer of Height Datum Across Seas Using GPS Leveling, Gravimetric Geoid and Corrections Based on a Polynomial Surface[J]. Computers and Geosciences, 2013, 51:135-142 |
| [11] | Xie Yong, Fan Dongming. Study on GPS Height Transformation Based on EGM2008[J]. Surveying and Mapping, 2010,33(5):204-208(谢用, 范东明. 基于EGM2008地球重力场模型的GPS高程转换研究[J]. 测绘, 2010, 33(5):204-208) |
| [12] | Zhu Yaguang, Gao Xingguo, Liu Yanxiong, et al. Elevation Determination Based on EGM2008 Mode[J]. Journal of University of Jinan,2011,25(4):410-413(朱亚光, 高兴国, 刘焱雄, 等. 基于EGM2008重力场模型的高程联测方法[J]. 济南大学学报, 2011, 25(4):410-413) |
| [13] | Shu Chanfang, Li Feihong, Zhang Liming. Local Height Datum Unification Using EGM2008[J]. Progress in Geophysics, 2011,26(2):438-442(束蝉方, 李斐弘, 张利明. 基于EGM2008重力场模型的局部高程基准统一[J]. 地球物理学进展, 2011, 26(2):438-442) |
| [14] | Gu Yanchao, Fan Dongming. Study on GPS Height Transformation by Combining EGM2008 and Residual Terrain Model[J]. Engineering of Surveying and Mapping,2013,22(2):26-29(谷延超, 范东明. 顾及EGM2008和残差地形模型的GPS高程转换方法研究[J].测绘工程, 2013, 22(2):26-29) |
| [15] | Zhang Xingfu, Liu Cheng. The Approach of GPS Height Transformation Based on EGM2008 and SRTM/DTM2006.0 Residual Terrain Model[J]. Acta Geodaetica et Cartographica Sinica,2012,41(1):25-32(张兴福, 刘成. 综合EGM2008模型和SRTM/DTM2006.0省略剩余地形模型的GPS高程转换方法[J].测绘学报, 2012, 41(1):25-32) |
| [16] | Ning Jinsheng, Luo Zhicai, Yang Zhanji, et al. Determination of Shenzhen Geoid with 1 km Resolution and Centimeter Accuracy[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(2):103-107(宁津生, 罗志才, 杨沾吉, 等. 深圳市1 km高分辨率厘米级高精度大地水准面的确定[J]. 测绘学报, 2003, 32(2):103-107) |
| [17] | Nikolaos K P, Simon A H. An Earth Gravitational Model to Degree2160:EGM2008[OL]. http://www.massentransporte.de/fileadmin/2kolloquium_muc/2008-10-08/Bosch/EGM 2008. pdf, 2008 |
| [18] | Zhang Xingfu, Liu Cheng, Liu Hongxin. Accuracy Validation of EGM2008 Model Using GPS Leveling Data[J]. Bulletin of Surveying and Mapping, 2009,2:7-9(张兴福, 刘成, 刘红新. 利用GPS水准数据检核EGM2008重力场模型的精度[J]. 测绘通报, 2009, 2:7-9) |
| [19] | Nikolaos K P, Simon A H, Steve C K. The Development and Evaluation of the Earth Gravitational Model 2008(EGM2008)[J]. Journal of Geophysical Research, 2012,117:1-38 |
| [20] | Wang Jianqiang, Li Jiancheng, Wang Zhengtao, et al. Pole Transform of Spherical Harmonic Function to Quickly Calculate Gravity the Disturbance on Earth-Orbiting Satellites[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9):1039-1043(王建强, 李建成, 王正涛, 等. 球谐函数变换快速计算扰动引力[J]. 武汉大学学报·信息科学版, 2013, 38(9):1039-1043) |
| [21] | Martina G, Tomislav B. Height Transformation Models from Ellipsoidal into the Normal Orthometric Height System for the Territory of the City of Zagreb[J]. Studia Geophysica et Geodaetica, 2009, 53(1):17-38 |
| [22] | Tadayoshi F. Estimation of Prediction Error by Using K-fold Cross-validation[J]. Statistics and Computing, 2011, 21:137-146 |
 2016, Vol. 41
2016, Vol. 41


