文章信息
- 刘凤珠, 张景雄, 林宗坚, 阳柯
- LIU Fengzhu, ZHANG Jingxiong, LIN Zongjian, YANG Ke
- 多光谱遥感影像的灰度与纹理信息测度方法
- Measurement of Graylevel and Texture Information in Multispectral Images
- 武汉大学学报·信息科学版, 2016, 41(3): 415-420
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 415-420
- http://dx.doi.org/10.13203/j.whugis20140329
-
文章历史
- 收稿日期: 2014-12-10

2. 中国测绘科学研究院, 北京, 100039
2. Chinese Academy of Surveying and Mapping, Beijing 100039, China
遥感影像具有内容丰富、大视野、现势性强等显著优点,在资源普查、环境监测、抗震救灾中具有广泛应用。影像的光谱特征以不同的DN(digital number)组反映于影像上。地物的空间特征—纹理结构,以灰度值之间的关系表现,它反映出地表辐射的空间分布状况。遥感分析和解译的基本依据是灰度(光谱)和纹理(空间)两方面的信息,合理而有效地度量灰度信息量和纹理信息量有助于影像波谱信息和空间信息的有效利用。
1948年Shanoon严格定义了信息熵的概念[1],并得到发展应用,成为一种常用的影像信息度量方法。Blacknell对基于信息熵和信噪比的信息量计算方法进行对比,并考虑了椒盐噪声的影响[2];林宗坚等讨论了遥感与GIS数据的信息量及不确定性[3];王占宏等利用马尔科夫信源原理确定影像相关范围并计算影像信息量[4];Razlighi等用马尔可夫随机场模型计算影像空间熵[5]。一般信道中有干扰(噪声)的存在,导致信号接收后对输入信号尚存在不确定性(疑义)[6]。遥感影像的获取过程中不可避免地引入噪声,获取的影像包含噪声,导致信息熵的增加,从而使得估算结果包含无用的信息量[7]。另外,受影像邻元相关性和波段间相关性的影响,影像存在大量的信息冗余。
本文选用散点图法估计影像的观测噪声,用差值脉冲编码调制(differential pulse code modulation,DPCM)压缩方法消除影像波段内和波段间相关性的影响,用参数熵模型来模拟无噪声且不相关的影像信号,据此计算信源的有用(或有效)信息量。本文提出将此方法用于原始波段影像和派生纹理影像及其组合影像的信息度量;利用Landsat TM影像进行了信息量估计与分析实验,分别统计灰度信息量与纹理信息量及其的组合信息。
1 方 法 1.1 噪声估计国内外学者们提出了多种噪声评估方法[8, 9, 10, 11]。Lee提出了散点图估计遥感影像噪声方法[12],其基本思想是将匀质区方差视为影像噪声方差,假设噪声为独立的加性噪声,影像模型为:
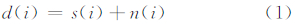
式中,d表示DN值;s表示信号;n表示噪声。其方差关系可表示为:

将整幅影像划分小块,对于小块的均质区域,其均值和方差可以表示为:
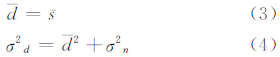
根据小块均质区的d和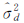 画散点图,并拟合水平回归线,直线在Y方向上的截距即为噪声方差的估计值
画散点图,并拟合水平回归线,直线在Y方向上的截距即为噪声方差的估计值 。本文在不进行人工干预的情况下,运用了自动提取均质区域的方法,在很大程度上提高了该算法的自动化程度。由于受边缘和纹理信息的影响,使得对应区域散点远离聚集区。通过设计阈值,不断剔除方差较大的散点,直至噪声方差趋于稳定或变化很小时停止计算。
。本文在不进行人工干预的情况下,运用了自动提取均质区域的方法,在很大程度上提高了该算法的自动化程度。由于受边缘和纹理信息的影响,使得对应区域散点远离聚集区。通过设计阈值,不断剔除方差较大的散点,直至噪声方差趋于稳定或变化很小时停止计算。
遥感影像去相关处理的主要目的是消除冗余信息(包括波段内和波段间)。差分脉冲编码调制、离散余弦变换、离散小波变换均得到了广泛应用[13, 14, 15]。本文将DPCM压缩编码用于二维影像去相关,并扩展到三维方向,用以消除谱间相关性。
像素预测估计值,可由相邻像元的实际值预测而得:

式中,{Φ(j),j=1,…,P}是线性预测器的预测系数,使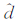 (i)逼近d(i),采用均方误差最小的准则(MMSE),得到最佳预测系数Φ(j)。
(i)逼近d(i),采用均方误差最小的准则(MMSE),得到最佳预测系数Φ(j)。
将影像噪声模型式(1)代入式(5),可以得到:

式中,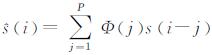 表示无噪声信号的预测值,由此d的预测误差可以定义为:
表示无噪声信号的预测值,由此d的预测误差可以定义为:
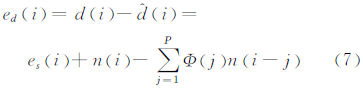
预测误差式(7)的方差即为:
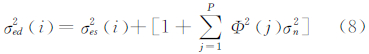
式中,影像预测误差的方差σed2(i)和预测系数Φ(j)可由原始影像计算而得,影像噪声方差可由§1.1噪声估计过程中得到。因此,可以得到二维无噪声信号的方差σes2(i)。
将2D DPCM压缩编码扩展到三维。与二维处理不同的是,预测器的设计需从原来的一个波段扩展到N个波段。假设第K波段为当前波段,k-1,k-2,…,k-i 分别表示与第K波段相邻的第1、2和第i个波段。最终的预测系数为{Φ(j),j=1,…,P}(2D)和{Ψ(m),m=1,…,Q}(3D)此时,式(8)可表示为:
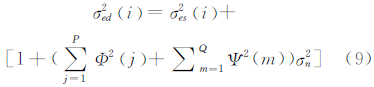
由于波段间的相关性各不相同,可根据波段间相关性的强弱顺序来选择预测顺序。
1.3 信息量估算 1.3.1 参数熵模型假设无记忆信源S,其概率密度函数(PDF)为p(x),信息熵H可定义为[16, 17]:

式中,c为常数(0< c ≤2πe),决定了信源的分布。当c=2πe时,信源具有高斯分布,此时信息熵具有最值log2√2πeσ2。
信息量的大小只与信号分布有关即只与常数c有关。用Hs来表示信号的信息量,cs表示其在参数熵模型中对应的参数,我们的目的在于确定仅与信号分布有关的常数cs,并利用公式来估算影像信号信息量。
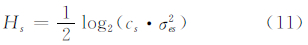
为了得到DPCM编码后预测误差的分布,用广义高斯概率密度函数(generalized gaussian density,GGD)来拟合预测误差分布曲线,得到预测误差的分布函数。GGD的定义为:
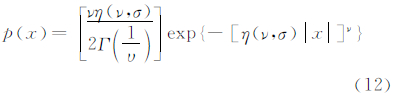
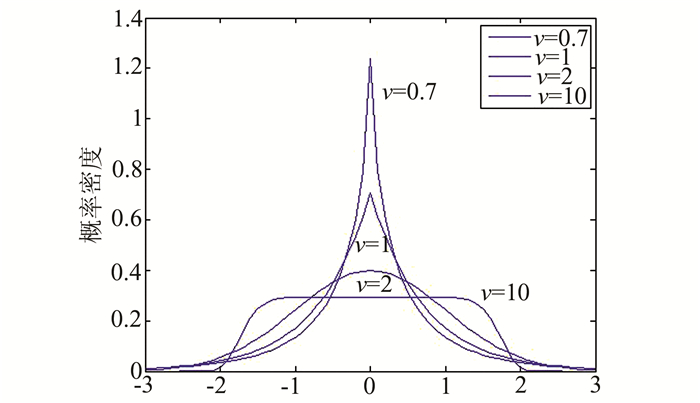
式中,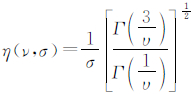 是Gamma函数,σ是GGD的标准差,ν是形状参数,决定了GGD的形状,图 1反映了广义高斯概率密度函数随形状参数的变化情况。将p(x)代入式(10)得到熵函数FH:
是Gamma函数,σ是GGD的标准差,ν是形状参数,决定了GGD的形状,图 1反映了广义高斯概率密度函数随形状参数的变化情况。将p(x)代入式(10)得到熵函数FH:
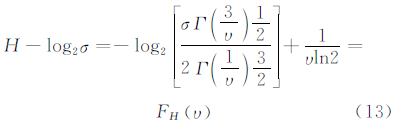
式中,σ可以通过真实数据求得,形状参数ν可以通过式(14)求得:
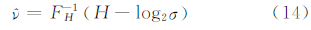
并且,

由式(15)可得到信号熵参数cs。
|
| 图 1 广义高斯概率密度函数图 Fig. 1 Generalized Gaussian Density |
假设原始影像(此处影像可以是纹理影像)的预测误差可以用GGD模型来模拟,由式(13)可得:
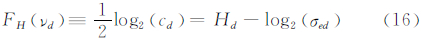
式中,νd是σed的形状参数;Hd是离散信源的熵值。通过式(16)和式(13)可计算出形状参数νd。
由信号和噪声关系可知,影像预测误差的概率密度函数Ped是信号概率密度函数Pes和噪声概率密度函数PN的线性卷积结果:

空间域的卷积可以简化为频率域的乘法[18, 19]。在具体处理过程中,在频率域做除法实现去卷积过程,从而得到es的概率密度函数pes(x),再由式(15)得到仅与信号分布有关的常数cs,根据式(11)得到影像信息量。
2 实例与分析 2.1 实验数据本文实验数据选择一幅512像素×512像素武汉城区的TM影像的6个波段(去除分辨率较低的第6波段)。图 2为6个波段的TM影像。

|
| 图 2 武汉城区TM影像(512像素×512像素) Fig. 2 The 512×512 Details from the Landsat TM Images of Wuhan |
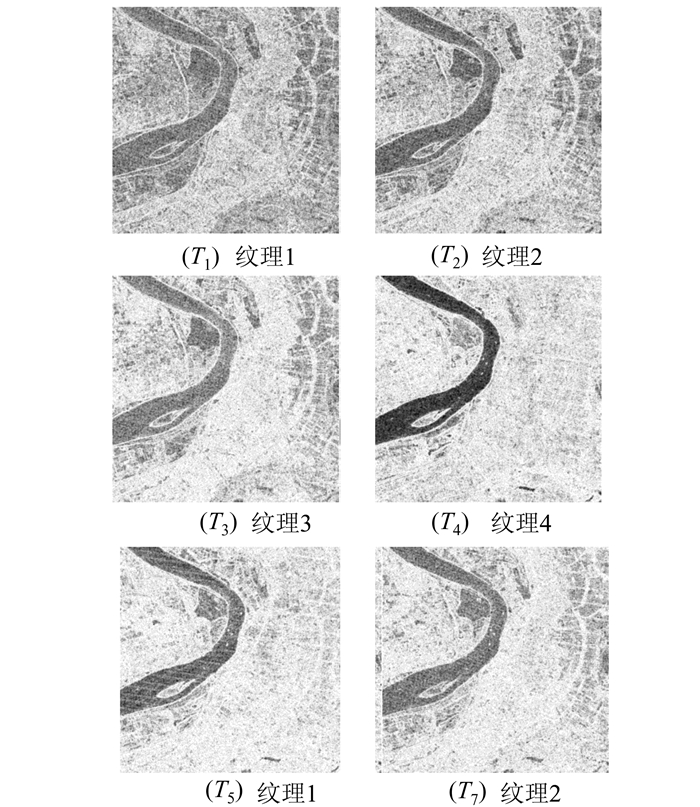
Haralick等一共定义了14 种纹理特征计算方法。本文选取其中的5种常用纹理特征统计量,即均值、方差、对比度、灰度相关和熵[18]。分别以3像素×3像素 、5像素×5像素 和7像素×7像素窗口提取纹理特征数据。然后,将提取到的纹理特征数据做归一化处理,形成纹理图像。可以发现,熵作为特征统计量且纹理提取窗口为3像素×3 像素时可获得更多纹理差异的细节信息。因此,本文以3像素×3像素的窗口对TM影像的6个波段提取纹理特征并生成灰度影像相对应的纹理影像(图 3)。
|
| 图 3 纹理影像 Fig. 3 The 512×512 Details from the Texture Images of Wuhan |
用散点图法对灰度影像(B1、B2、B3、B4、B5和B7)进行噪声估计,并分别对二维灰度影像进行2D DPCM编码,拟合模型参数并分别计算单波段灰度影像的信息量(统计结果见表 1)。
| 波段 | 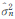 | σ2es | cs | H | Hd | Hs |
| B1 | 2.10 | 16.32 | 15.7 | 5.15 | 4.11 | 4.00 |
| B2 | 1.17 | 30.80 | 14.3 | 5.57 | 4.46 | 4.39 |
| B3 | 1.96 | 101.5 | 11.7 | 6.33 | 5.27 | 5.18 |
| B4 | 0.40 | 139.2 | 11.4 | 6.53 | 5.40 | 5.31 |
| B5 | 1.10 | 222.9 | 10.3 | 6.89 | 5.70 | 5.58 |
| B7 | 1.49 | 123.0 | 11.5 | 6.42 | 5.33 | 5.23 |
| 平均 | 1.37 | 105.6 | 12.48 | 6.14 | 5.05 | 4.95 |
表 1为样区TM 6个波段数据的统计分析结果,其中 是噪声方差的估计值,σ2es是无噪声影像信号的方差,cs是信号熵参数,H是原始影像的信息熵(bit/pix),Hd是含噪声不相关影像信号的信息熵(bit/pix),Hs是无噪声且不相关的影像信号的信息熵(bit/pix),即二维影像的有用信息量。从表 1中可见,TM影像的6个波段中B5(波段5)的信息量最大(5.58 bit/pix),其次是B4、B7、B3、B2、B1。这表明B5的地物间差异可能表现最大,波谱信息最丰富。另外,经过2D DPCM 压缩之后平均像元的信息熵减少了1.06 bit/pix(压缩前为6.14 bit/pix;压缩后为5.05 bit/pix),表明由于空间相关性的存在,直接用信息熵评价影像信息量,其结果存在近20%的信息冗余。
是噪声方差的估计值,σ2es是无噪声影像信号的方差,cs是信号熵参数,H是原始影像的信息熵(bit/pix),Hd是含噪声不相关影像信号的信息熵(bit/pix),Hs是无噪声且不相关的影像信号的信息熵(bit/pix),即二维影像的有用信息量。从表 1中可见,TM影像的6个波段中B5(波段5)的信息量最大(5.58 bit/pix),其次是B4、B7、B3、B2、B1。这表明B5的地物间差异可能表现最大,波谱信息最丰富。另外,经过2D DPCM 压缩之后平均像元的信息熵减少了1.06 bit/pix(压缩前为6.14 bit/pix;压缩后为5.05 bit/pix),表明由于空间相关性的存在,直接用信息熵评价影像信息量,其结果存在近20%的信息冗余。
将2D DPCM 编码压缩扩展至3D方向,根据波段间相关性的强弱顺序,确定最佳预测顺序并对当前波段的像元值进行预测。如在样区影像中,与第1波段相关性最强的是第2波段,其次是第3、4、7和5波段,最佳预测数顺序为1→2→3→4→7→5。其统计分析结果见表 2。
| B1 | B2 | B3 | B4 | B5 | B7 | |
| 2D 去相关 | 4.00 | 4.39 | 5.18 | 5.31 | 5.58 | 5.23 |
| 3D 去相关 | 2.12 | 2.47 | 3.76 | 4.54 | 3.85 | 3.73 |
| 差值 | 1.88 | 1.92 | 1.42 | 0.77 | 1.73 | 1.50 |
实验结果表明,3D DPCM编码压之后,由于消除了波段间的信息冗余,各个波段信息量对应减少,其中TM影像中1、2和3波段较强,5和7波段相关性存在较强相关,而第4波段相对独立,因此,在3D去相关之后B1、B2、B3、B4、B5和B7的信息量的减少量(达1.88,1.92,1.42,0.77,1.73,1.50 bit/pix)均大于第4波段信息量的减少量(仅0.77 bit/pix)。以上分析表明,针对该地区,TM 7个波段的数据中,B4的信息量最大,其次是B5、B3和B7,因而在该地区的土地资源调查中,波段的选择以B4、B5、B3为最佳。具体实践也表明采用B4、B5、B3赋予R,G,B的假彩色合成方案比常规的B2、B3、B4具有更好的解译效果[19]。
对TM影像派生的纹理影像的信息量进行估算并将灰度影像和纹理影像进行组合分析,进一步验证本文方法的有效性和普遍意义,其结果在表 3中显示。从表 3中看出,TM影像包含的纹理信息量更加丰富,均大于5 bit/pix,相比之下灰度(光谱)信息量却略显不足。纹理影像与灰度影像的综合分析的结果表明,纹理(空间)信息与灰度(光谱)信息之间并无直接制约关系。高分辨率影像空间信息更加丰富,地物目标的结构和纹理细节等信息更加突出。于是,在传统光谱分析的基础上结合影像纹理信息,可以提高对影像信息的利用。若将二维的灰度影像与其派生的纹理影像进行组合分析,所含信息将得到明显提高。实践也表明,引入纹理信息,可提高高分辨率影像分类和分割的精度。
| 单独分析 | 组合分析 | |
| T1 | 5.92 | 5.67 |
| T2 | 5.70 | 5.69 |
| T3 | 5.33 | 4.98 |
| T4 | 5.82 | 5.65 |
| T5 | 5.38 | 5.09 |
| T7 | 5.34 | 5.15 |
| B1 | 2.12 | 3.11 |
| B2 | 2.47 | 2.48 |
| B3 | 3.76 | 3.74 |
| B4 | 4.54 | 4.57 |
| B5 | 3.85 | 4.00 |
| B7 | 3.73 | 4.62 |
| 总和 | 53.96 | 54.75 |
本文还将此方法应用于TM影像主成分分析后主成分影像的信息量估算,并与传统的特征值法和方差统计信息量方法进行比较。前3个主分量虽然包含有95%的方差信息,但是从信息量评价的角度来看,前3个主分量仅占TM 影像总信息量的65%,各主成分特征值或方差的大小与信息量在趋势上保持一致,但比重不同。
3 结 语本文针对散点图估计噪声方法,运用自动化技术提取影像均质区域,避免了人工干预;其次,利用2D DPCM 和3D DPCM无损压缩方法消除影像的空间相关性和波谱相关性,并用参数熵模型来统计影像信息量。实验表明,本文方法可以较客观地评价噪声对信息熵的影响和影像相关性(空间和波段间相关性)造成的信息冗余。通过对TM影像灰度信息量及纹理信息量进行估计,进一步验证了该方法的普遍性和有效性。
本文仅对加性噪声进行评价,没有对噪声估计的效果及其对信息量计算的影响进行详细对比分析。在后续工作中,应探讨如何有效地估计噪声及不同压缩方法在信息量评价中效果,如何将光学影像信息和雷达影像信息进行统一度量。另外,雷达影像属复数型信号范畴,需特别关注。
| [1] | Shannon C E. A Mathematic Theory of Communication[J]. Bell System Technical Journal, 1948, 27(1):379-423 |
| [2] | Blacknell D, Oliver C J. Information Content of Coherent Image[J].Journal of Physics D:Applied Physics,1993, 26(9):1 364-1 370 |
| [3] | Lin Zongjian, Zhang Yonghong. Measurement of Information and Uncertainty of Remote Sensing and GIS Data[J].Geomatics and Information Science of Wuhan University, 2006, 31(7): 569-572(林宗坚, 张永红. 遥感与地理信息系统数据的信息量及不确定性[J]. 武汉大学学报·信息科学版, 2006, 31(7): 569-572) |
| [4] | Wang Zhanhong, Du Daosheng. Computing the Imagery Entropy by Using Markov Information Source Theory[J]. Remote Sensing Information, 2008, (3):26-30(王占宏,杜道生. 利用马尔科夫信源原理计算遥感影像信息量[J]. 遥感信息,2008(3):26-30) |
| [5] | Razlighi Q R,Kehtarnavaz N,Nosratinia A. Computation of Image Spatial Entropy Using Quadrilateral Markov Random Field[J]. IEEE Transactions on Image Processing, 2009, 18(12):2 629-2 639 |
| [6] | Atkinson P M, Atkinson, I M, Sargent G M,et al. Exploring the Geostatistical Method for Estimating the Signal-to-Noise Ratio of Images[J].Photogrammetric Engineer & Remote Sensing,2007, 73(7):841-850 |
| [7] | Huck F O,Fales C l,Alter-Gratenberg R. Information-Theoretic Assessment of Sampled Imaging System[J].Optional Engineering, 1999,38(5):742-762 |
| [8] | Luo Zhicai, Lin Xu, Zhou Boyang, et al. The Application of a Novel Variance Testing Method for Compatibility Analysis of Datum Points in Engineering GPS Network[J].Geomatics and Information Science of Wuhan University, 2012, 31(10): 1 164-1 167(罗志才,林旭,周波阳,等.自协方差最小二乘噪声估计的改进算法[J].武汉大学学报·信息科学版, 2012, 31(10): 1 164-1 167) |
| [9] | Fu Peng, Sun Quansen, Ji Zexuan, et al. A Method of SNR Estimation and Comparison for Remote Sensing Images[J].Acta Geodaetica et Cartographica Sinica,2013, 42(4):559-567(傅鹏,孙权森,纪则轩,等.一种遥感图像信噪比评估和度量准则[J]. 测绘学报,2013,42(4):559-567) |
| [10] | Gao Lianru, Zhang Bing, Zhang Xia, et al. Study on the Method for Estimating the Noise in Remote Sensing Images Based on Local Standard Deviations[J]. Journal of Remote Sensing, 2007, 11(2): 201-208(高连如, 张兵, 张霞,等.基于局部标准差的遥感图像噪声评估方法研究[J].遥感学报,2007, 11(2): 201-208) |
| [11] | Qin Bangyong, Hong Bo, Zhang Zhi, et al. A Generally Applicable Noise—Estimating Method for Remote Sensing Images[J]. Remote Sensing Letters,2014,5(5):481-482 |
| [12] | Lee J S,Hoppel K.Noise Modeling and Estimation of Remotely Sensed Images[J]. IEEE Geoscience and Remote Sensing, 1989, 2(1): 1 005-1 008 |
| [13] | Wang Jinfei, Zhang Kaizhong, Tang Shouwen. Spectral and Spatial Decorrelation of Landsat-TM Data for Lossless Compression[J].Transactions on Geoscience and Remote Sensing, 1995, 33(5): 1 277-1 285 |
| [14] | Chen T M, Staelin D H, Arps R B. Information Content Analysis of Landsat Image Data for Compression[J]. Transactions on Geoscience and Remote Sensing, 1987,25(4):499-501 |
| [15] | Roger R E. Lossless Compression of AVRIS Images[J].Transactions on Image Processing,1996,5(5):713-719 |
| [16] | Jayant N S, Noll P. Digital Coding of Waveforms:Principles and Applications to Speech and Video[M]. New Jersey:Prentice-Hall, 1984 |
| [17] | Aiazzi B,Baronti S, Santurri L, et al. Information-theoretic Assessment of Multi-dimensional Signals[J].Signal Processing,2005, 85(2 005): 903-916 |
| [18] | Haralick R M.Texture Featuresfor Image Classification[J].Transactions on Systems, Man, and Cybernetics, 1990, 3(6): 610-621 |
| [19] | Tang Yunwei, Zhang Jingxiong. Area-to-point Cokriging and Multiple-point Geostatistical Simulation for Remotely Sensed Image Fusion[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 856-861(唐韵玮,张景雄.基于面-点协同克里格和多点地统计模拟的遥感影像融合方法[J].武汉大学学报·信息科学版, 2014, 39(7): 856-861) |
 2016, Vol. 41
2016, Vol. 41



