文章信息
- 王宇谱, 吕志平, 陈正生, 黄令勇, 李林阳, 宫晓春
- WANG Yupu, LV Zhiping, CHEN Zhengsheng, HUANG Lingyong, LI Linyang, GONG Xiaochun
- 一种新的钟差预处理方法及在WNN钟差中长期预报中的应用
- A New Data Preprocessing Method for Satellite Clock Bias and Its Application in WNN to Predict Medium-term and Long-term Clock Bias
- 武汉大学学报·信息科学版, 2016, 41(3): 373-379
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 373-379
- http://dx.doi.org/10.13203/j.whugis20140216
-
文章历史
- 收稿日期: 2014-10-19

2. 地理信息工程国家重点实验室, 陕西 西安, 710054;
3. 火箭军工程大学, 陕西 西安, 710025
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of High-Tech, Xi'an 710025, China
当卫星导航系统的地面控制部分由于战争等因素陷入瘫痪状态时,要维持卫星导航系统的正常运行,地面需提供相当时长及一定精度的卫星钟差作为先验信息。因此,卫星钟差的中长期预报很有必要[1]。目前,针对钟差预报的问题已有大量研究,并且建立了多种预报模型[2, 3, 4, 5, 6, 7, 8, 9]。将这些钟差预报模型概括起来主要包括多项式预报模型[2](主要是二次多项式模型,QP)、灰色系统模型[3](主要为GM(1,1)模型,GM)、谱分析模型[4](SA)、时间序列模型[5](ARIMA模型)、Kalman滤波模型[6](KF)、最小二乘支持向量机模型[7](LSSVM)、小波神经网络模型[8](WNN)等。但是这些模型在预报中各有其特点:QP预报钟差时其预报误差会随着预报时间的增加而显著变大[3],GM(1,1)预报精度受模型指数系数影响较大[10, 11],SA的周期函数要根据较长的钟差序列才能可靠确定,ARIMA存在模式识别和模型定阶的困难[12],KF的优劣取决于对原子钟运行特性、随机先验信息等的认知程度[13],LSSVM的核函数参数选择对预报效果有较大影响[7, 14],WNN面临难以确定隐含层节点数和缺乏在钟差中长期预报中的应用研究[8, 15]。在这些模型中,QP模型、GM(1,1)和KF模型是较为常用且具有代表性的预报模型。
本文在提出一种针对钟差一次差分序列的数据预处理方法的基础上,建立了一种钟差中长期预报的小波神经网络模型。使用GPS卫星铷钟钟差数据进行预报,并与常用的3种模型进行对比,结果表明,本文方法能够有效地减小星载铷钟钟差的中长期预报误差。
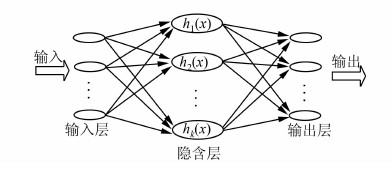
1 算法原理 1.1 钟差预报的小波神经网络模型[8]WNN模型是一种新兴的预报模型,该模型通过对历史数据的学习便可进行相对精确的预报。图 1是一种常见的具有三层结构的紧致型小波神经网络的结构,其中隐含层的hk(x)函数为小波基函数。
|
| 图 1 三层结构的小波神经网络模型 Fig. 1 A Wavelet Neural Network Model with Three-Layer Structure |
使用WNN模型进行预报时,需要解决的一个比较关键的问题是针对特定预报对象的较为合适的网络模型拓扑结构的确定。对于导航卫星钟差的预报,文献[8]提出一种卫星钟差预报的小波神经网络算法:首先对已知钟差数据L={l(i),i=1,2,…,n}进行相邻历元间的一次差分,即l(i)-l(i-1),进而得到钟差数据对应的钟差一次差分序列ΔL={Δl(i)=l(i)-l(i-1),i=2,…,n};然后根据钟差一次差分序列对WNN进行建模,利用所建模型预报第n历元以后m(m≥1)个历元的钟差一次差分序列预报值ΔL1={Δl(j),j=n+1,n+2,…,n+m};最后将预报的一次差分序列与已知钟差值l(n)对应相加,便可得到所需时刻的预报钟差,即有:

通过这种方法使得WNN模型在隐含层节点数很少的情况下就能实现对钟差的有效预报。本文用于钟差中长期预报的WNN是在文献[8]算法的基础上建立的,采用的WNN模型结构、学习训练算法和小波基函数与文献[8]相同。
1.2 基于钟差一次差分序列的数据预处理方法在导航卫星钟差数据处理中,星载原子钟的钟差数据和频率数据间的转换关系式为[2]:
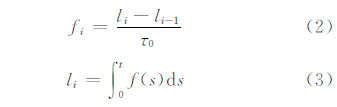
式中,li为第i历元的钟差值;τ0为第i历元和i-1历元间的时间间隔。对于给定的钟差数据序列,τ0为已知的常数;fi为采样时间间隔为τ0的第i历元的频率值。
为了高精度地记录时间信息,通常钟差的数据有效位数多、数据数值相对较大,容易掩盖一些受粗差等影响的异常数据点[16]。星载原子钟正常情况下是比较稳定的,相邻历元间钟差数据的数值变化相对较小;相邻历元一次差分可降低原钟差序列趋势项的影响得到一组有效数字位数减少且数值较小的数据序列,即钟差一次差分序列(对应于式(2)右边的分母部分)。一次差分数据再除以钟差相邻历元的时间间隔便将相位数据转化为频率数据。
频率数据相对于相位数据,其有效位数减少并且数据的数值也变小,这样便于异常值的识别;同时,异常的钟差数据对应于频率数据的峰值,而峰值较易进行探测。因此,针对钟差数据的异常值识别一般是在其对应的频率数据上进行的[2, 16]。
对比钟差一次差分数据Δl(i)=l(i)-l(i-1)与钟差数据对应的频率数据fi=(li-li-1)/τ0可以发现,两者在形式上仅相差一个常数τ0。钟差一次差分数据Δl组成的数据序列与钟差频率数据f=Δl/τ0组成的频率数据序列相比,前者相当于给后者整体扩大了τ0倍,但这种扩大并不改变数据序列内部各元素之间的比值。因此,在数据序列中出现异常值时,两者皆会出现一个峰值,而峰值则比较容易进行探测,便于异常值的识别。
在使用WNN进行预报时,建模数据中的异常值对模型的预报性能有影响,会影响模型的预报精度。文献[8]在使用钟差一次差分序列对WNN进行建模时,没有考虑一次差分序列出现异常值的情况。针对钟差一次差分序列具有数据有效位数和数据数值较小的特点,可以借鉴频率数据异常值探测的方法对用于WNN建模的钟差一次差分数据进行预处理,从而进一步提高WNN模型预报钟差时的性能。
本文采用一种基于改进中位数的异常值探测方法对钟差一次差分数据进行预处理。该方法的基本思路为,将每个钟差一次差分数据Δl(i)与一次差分序列的中数(MED)k及中位数(MAD)数倍之和进行比较;若钟差一次差分值满足
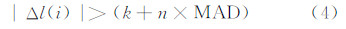
则认为该一次差分数据是异常值,同时剔除该值,然后用内插的方法来补充该点数据。本文用三次分段样条方法对剔除历元对应的钟差值进行内插。
式(4)中,k=Median{Δl(i)};MAD=Median{|Δl(i)-k|/0.674 5},Median表示取中位数。n的取值根据需要进行确定,本文遵循的原则是设置的n值要保证探测出的异常值个数不能超过建模数据总数的10%,因为这样既可以一定程度上避免剔除有效信息又能降低异常值对WNN模型预报性能的影响。将使用本文预处理方法后的WNN模型记为D-WNN模型。
2 算例与分析本文使用IGS(international GNSS service)提供的GPS系统15 min采样间隔的精密钟差数据进行预报试验。考虑到目前我国北斗系统使用的星载原子钟均为铷钟,GPS系统的星载原子钟也主要是铷钟,因此,本文以GPS星载铷钟的钟差数据进行预报,具体为使用2013-07-03的钟差数据分别进行接下来7、15、30和60 d的预报。同时,该时间段内的GPS星载铷钟有4种类型,即BLOCK IIF Rb、BLOCK IIR-M Rb、BLOCK IIR Rb和BLOCK IIA Rb,本文从每种类型中任选一颗卫星进行试验,具体选取的分别是PRN01、PRN05、PRN22和PRN32 4颗卫星(当然也可使用剩余相应类型的卫星,并不会影响试验和结论)。试验中以预报时间段对应的IGS精密钟差值为真值,采用均方根误差(RMS)和平均误差(Mean)评价预报结果的精度;利用最大、最小误差之差的绝对值(Range)评价算法进行预报时的稳定性。其中均方根误差计算公式为:

式中,ti是IGS精密钟差;t为钟差预报值。
2.1 算例一首先通过试验来说明本文所提数据预处理方法的有效性。针对建模数据,使用本文预处理方法时4颗卫星对应式(4)中n的取值分别为:PRN01取n=2,PRN05取n=8,PRN22取n=1,PRN32取n=1。以预报15 d为例,对比分析4颗卫星数据预处理前后的预报结果。本文给出了PRN01卫星的预报结果图,剩余的3颗卫星给出预报结果的统计值(后面算例类似)。图 2(a)、2(b)分别为PRN01卫星在使用预处理方法前后时的预报结果和预报误差图。

|
| 图 2 PRN01卫星钟差数据预处理前、后预报结果和预报误差 Fig. 2 Clock Bias Prediction Results and Errors of Satellite PRN01 Before and After the Data Preprocessing |
从图 2可以看出,PRN01卫星在使用WNN模型进行钟差的中期预报时,采用本文所提预处理方法得到的预报结果好于不使用预处理方法时的结果。为了充分说明本文所提预处理方法的优势,表 1给出了使用预处理方法前后4颗卫星预报结果的统计情况。
| /ns | ||||||||||||
| 方法 | PRN | |||||||||||
| 01 (IIF Rb) | 05 (IIR-M Rb) | 22 (IIR Rb) | 32 (IIA Rb) | |||||||||
| RMS | Mean | Range | RMS | Mean | Range | RMS | Mean | Range | RMS | Mean | Range | |
| WNN | 24.512 | 17.966 | 52.858 | 33.927 | 23.777 | 81.392 | 112.404 | -91.436 | 179.061 | 107.469 | 73.843 | 260.590 |
| D-WNN | 15.532 | 8.218 | 47.162 | 13.484 | -7.400 | 43.394 | 28.908 | -13.796 | 75.453 | 82.994 | 64.782 | 171.594 |
对比表 1中同一颗卫星的统计值,从预报结果的RMS和Mean值可以看出,D-WNN模型的预报精度均优于WNN模型的预报精度;而根据预报结果的Range值则可看出,D-WNN模型的预报稳定性也均优于WNN模型的预报稳定性。这说明在使用钟差一次差分序列对WNN进行建模时,序列中的异常数据对该模型的预报性能有影响;而通过本文所提的预处理方法对一次差分序列进行处理,能够提高WNN模型的预报性能,进而提高了钟差预报的精度与稳定性。因此,使用本文所提数据预处理方法能够提高基于钟差一次差分数据的WNN钟差预报模型的预报效果。
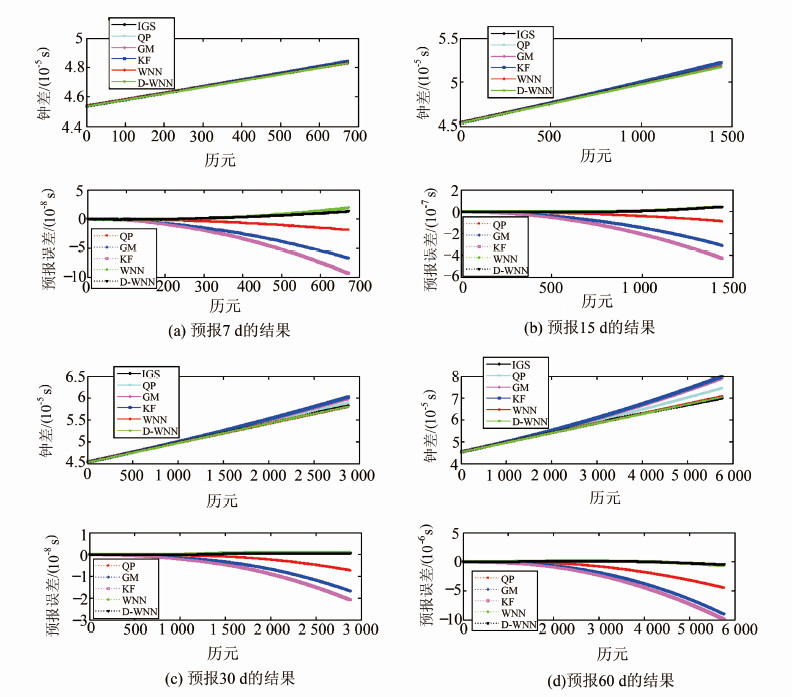
2.2 算例二为了进一步对比分析D-WNN模型在钟差中长期预报时的特点,图 3给出了PRN01卫星在使用QP模型、GM(1,1)、KF模型(本文使用基于方差递推法的Kalman滤波模型[11])和本文所提D-WNN模型分别进行7 d、15 d、30 d和60 d预报时的预报结果图。表 2~表 5给出了4颗卫星分别进行7 d、15 d、30 d及60 d预报时的预报结果统计情况。
|
| 图 3 PRN01卫星的钟差预报结果 Fig. 3 Prediction Results of Satellite PRN01 |
| /ns | ||||||||||||
| 方法 | PRN | |||||||||||
| 01 (IIF Rb) | 05 (IIR-M Rb) | 22 (IIR Rb) | 32 (IIA Rb) | |||||||||
| RMS | Mean | Range | RMS | Mean | Range | RMS | Mean | Range | RMS | Mean | Range | |
| QP | 8.727 | -6.570 | 19.386 | 29.094 | -22.915 | 61.082 | 198.849 | -151.215 | 433.850 | 145.674 | -111.937 | 315.382 |
| GM | 30.924 | -23.581 | 67.620 | 7.514 | 5.168 | 18.379 | 45.862 | -33.379 | 104.362 | 38.011 | 29.405 | 81.899 |
| KF | 42.260 | -31.666 | 93.959 | 147.808 | 111.104 | 327.003 | 327.638 | -247.242 | 721.420 | 232.183 | -175.765 | 510.859 |
| WNN | 7.487 | 4.376 | 20.828 | 8.088 3 | 5.525 | 19.851 | 49.409 | 36.968 | 108.179 | 36.652 | 27.580 | 81.798 |
| D-WNN | 5.623 | 3.815 | 13.745 | 6.786 | 4.291 | 18.273 | 17.905 | -5.635 | 59.356 | 25.718 | 19.646 | 54.110 |
| /ns | ||||||||||||
| 方法 | PRN | |||||||||||
| 01 (IIF Rb) | 05 (IIR-M Rb) | 22 (IIR Rb) | 32 (IIA Rb) | |||||||||
| RMS | Mean | Range | RMS | Mean | Range | RMS | Mean | Range | RMS | Mean | Range | |
| QP | 39.043 | -29.197 | 89.025 | 116.911 | -89.355 | 254.754 | 787.888 | -605.959 | 1 650.947 | 631.022 | -475.589 | 1 399.561 |
| GM | 137.012 | -102.698 | 308.233 | 36.922 | 27.062 | 84.084 | 146.886 | -118.493 | 238.287 | 141.932 | 109.564 | 300.675 |
| KF | 191.492 | -143.030 | 429.059 | 660.235 | 494.417 | 1 467.905 | 1 378.608 | -1 046.695 | 2 972.054 | 1 039.486 | -778.631 | 2 316.738 |
| WNN | 24.512 | 17.966 | 52.858 | 33.927 | 23.777 | 81.392 | 112.404 | -91.436 | 179.061 | 107.469 | 73.843 | 260.590 |
| D-WNN | 15.532 | 8.218 | 47.162 | 13.484 | -7.400 | 43.394 | 28.908 | -13.796 | 75.453 | 82.994 | 64.782 | 171.594 |
| /ns | ||||||||||||
| 方法 | PRN | |||||||||||
| 01 (IIF Rb) | 05 (IIR-M Rb) | 22 (IIR Rb) | 32 (IIA Rb) | |||||||||
| RMS | Mean | Range | RMS | Mean | Range | RMS | Mean | Range | RMS | Mean | Range | |
| QP | 277.455 | -185.469 | 733.847 | 438.953 | -331.414 | 968.899 | 2 715.120 | -2 074.609 | 5 917.433 | 2 441.253 | -1 833.100 | 5 402.483 |
| GM | 686.736 | -488.973 | 1 676.799 | 152.683 | 113.040 | 343.553 | 249.730 | -215.451 | 432.793 | 530.244 | 399.502 | 1 186.700 |
| KF | 881.833 | -638.403 | 2 089.777 | 2 609.582 | 1 949.741 | 5 818.422 | 5 078.992 | -3 837.183 | 11 202.944 | 4 093.981 | -3 062.216 | 9 105.494 |
| WNN | 70.303 | 54.368 | 106.611 | 148.931 | 111.433 | 334.257 | 185.833 | 163.980 | 284.456 | 488.266 | 348.775 | 1 149.496 |
| D-WNN | 41.137 | 30.935 | 64.919 | 51.738 | 9.949 | 178.173 | 76.182 | -61.437 | 150.789 | 353.853 | 263.532 | 811.584 |
| /ns | ||||||||||||
| 方法 | PRN | |||||||||||
| 01 (IIF Rb) | 05 (IIR-M Rb) | 22 (IIR Rb) | 32 (IIA Rb) | |||||||||
| RMS | Mean | Range | RMS | Mean | Range | RMS | Mean | Range | RMS | Mean | Range | |
| QP | 1 837.745 | -1 264.179 | 4 483.903 | 1 695.890 | -1 273.637 | 3 746.434 | 10 099.924 | -7 637.907 | 22 261.721 | 9 487.584 | -7 113.162 | 21 045.965 |
| GM | 3 745.295 | -2 645.860 | 9 010.866 | 624.083 | 462.414 | 1 419.825 | 426.904 | -380.179 | 671.864 | 2 161.669 | 1 604.652 | 4 892.053 |
| KF | 4 254.832 | -3 071.171 | 9 899.194 | 10 379.377 | 7 744.397 | 23 196.555 | 19 556.771 | -14 687.449 | 43 405.919 | 16 135.898 | -12 063.095 | 35 926.650 |
| WNN | 208.260 | 10.452 | 828.971 | 699.661 | 533.163 | 1 533.795 | 686.529 | 630.358 | 944.348 | 2 204.681 | 1 582.506 | 5 127.773 |
| D-WNN | 152.116 | 1.853 | 614.626 | 378.287 | 269.455 | 861.309 | 108.256 | -79.135 | 266.398 | 1 659.483 | 1 195.876 | 3 897.655 |
从图 3中看出,对PRN01卫星而言,相对于3种常用模型,WNN模型和D-WNN模型均能有效地抑制预报误差随着预报时间长度的增加不断增大的趋势,预报效果优于3种常规钟差预报模型的预报效果。
对比4个表中每颗卫星在不同预报时间长度时5种方法的预报结果,可以看出,对于4颗卫星,不论是表征预报结果精度的RMS和Mean,还是反映模型预报结果稳定性的Range,D-WNN模型的预报结果值均小于WNN模型相应的结果值,而这两种模型的预报结果值均小于3种常用模型相应的结果值;说明本文所提的预处理方法能够提高基于钟差一次差分WNN模型的预报效果,也说明了D-WNN模型预报结果的精度和稳定性均优于其他4种模型。因此,本文所提D-WNN模型可作为一种相对较好的钟差中长期预报模型。同时,在钟差中长期预报的实际应用中,首先对已知的建模钟差数据进行相邻历元间的一次差分,然后使用本文所提的数据预处理方法对钟差一次差分序列进行预处理,此后基于预处理后的一次差分序列对WNN建模,接着对所需预报时间段钟差对应的一次差分进行预报,最后将预报所得的一次差分还原为所需的钟差中长期预报结果。算例证明了该算法能够较好地进行钟差的中长期预报,对于地面控制部分异常时维持卫星导航系统正常运行具有较好的实用价值。
3 结 语本文在钟差预报小波神经网络模型的基础上,提出一种针对该模型的数据预处理方法,建立了一种适合钟差中长期预报的小波神经网络模型。使用GPS精密钟差数据分别进行7 d、15 d、30 d和60 d的钟差中长期预报,并将本文所建D-WNN模型与常用的QP模型、GM(1,1)、KF模型进行对比,结果表明,本文提出的D-WNN模型能够有效地抑制钟差中长期预报过程中预报误差随预报时间段的增加而不断变大的现象,而且其预报效果优于3种常用钟差预报模型的预报结果。该方法可以作为一种较好的卫星钟差中长期预报方法,为卫星自主导航定轨提供理论研究和实际应用参考。
| [1] | Xi Chao, Cai Chenglin, Li Simin, et al. Long-term Satellite Clock Bias Prediction Based on ARMA Model[J]. Acta Astronomica Sinica, 2014,55(1): 78-89 (席超,蔡成林,李思敏,等.基于ARMA模型的导航卫星钟差长期预报[J].天文学报,2014,55(1): 78-89) |
| [2] | Guo Hairong. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellite[D].Zhengzhou: Information Engineering University, 2006 (郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州:信息工程大学,2006) |
| [3] | Cui Xianqing, Jiao Wenhai. Grey System Model for the Satellite Clock Error Predicting[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 447-450 (崔先强,焦文海.灰色系统模型在卫星钟差预报中的应用[J].武汉大学学报·信息科学版,2005,30(5):447-450) |
| [4] | Zheng Zuoya, Dang Yamin, Lu Xiushan,et al. Prediction Model with Periodic Item and Its Application to the Prediction of GPS Satellite Clock Bias[J]. Acta Astronomica Sinica, 2010, 51(1):95-102(郑作亚,党亚民,卢秀山,等.附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J].天文学报,2010,51(1):95-102) |
| [5] | Zhao Liang, Lan Xiaoqi, Sheng Jianyue. Application of ARIMA Model in Satellite Clock Error Forecasting[J]. Journal of Water Resources and Architectural Engineering, 2012,10(1):135-137(赵亮,兰孝奇,盛建岳.ARIMA模型在卫星钟差预报中的应用[J].水利与建筑工程学报,2012,10(1):135-137) |
| [6] | Zhu Xiangwei, Xiao Hua. The Kalman Algorithm Used for Satellite Clock Offset Prediction and Its Performance Analysis[J]. Journal of Astronautics, 2008, 29(3): 966-970 (朱祥维,肖华.卫星钟差预报的Kalman算法及其性能分析[J].宇航学报,2008,29(3):966-970) |
| [7] | Lei Yu, Zhao Danning. Clock Error Prediction Using Least Squares Support Vector Machines[J]. Journal of Geodesy and Geodynamics, 2013,33(2):91-95(雷雨,赵丹宁.基于最小二乘支持向量机的钟差预报[J].大地测量与地球动力学,2013,33(2):91-95) |
| [8] | Wang Yupu, Lv Zhiping, Chen Zhengsheng, et al. Research the Algorithm of Wavelet Neural Network to Predict Satellite Clock Bias[J].Acta Geodaetica et Cartographica Sinica, 2013,42(3):323-330(王宇谱,吕志平,陈正生,等.卫星钟差预报的小波神经网络算法研究[J].测绘学报,2013,42(3):323-330) |
| [9] | Guo Hairong, Yang Sheng, Yang Yuanxi, et al. Numerical Prediction Methods for Clock Difference Based on Two-Way Satellite Time and Frequency Transform Data[J].Geomatics and Information Science of Wuhan University, 2007, 32(1): 43-46 (郭海荣,杨生,杨元喜,等.基于卫星双向时间频率传递进行钟差预报的方法研究[J].武汉大学学报·信息科学版, 2007, 32(1): 43-46) |
| [10] | Zheng Zuoya, Chen Yongqi, Lu Xiushan. An Improved Grey Model for the Prediction of Real-Time GPS Satellite Clock Bias[J]. Acta Astronomica Sinica, 2008, 49(3): 306-320(郑作亚,陈永奇,卢秀山.灰色模型修正及其在实时GPS 卫星钟差预报中的应用研究[J].天文学报,2008,49(3):306-320) |
| [11] | Lu Xiaofeng, Yang Zhiqiang, Jia Xiaolin, et al. Parameter Optimization Method of Gray System Theory for the Satellite Clock Error Predicating [J].Geomatics and Information Science of Wuhan University, 2008, 33(5): 492-495(路晓峰,杨志强,贾晓林,等.灰色系统理论的优化方法及其在卫星钟差预报中的应用[J].武汉大学学报·信息科学版,2008,33(5):492-495) |
| [12] | Zhang Qinghua, Sui Lifen, Mu Zhongkai. A GPS Precise Clock Errors Prediction Models Based on Wavelet and ARMA[J]. Journal of Geodesy and Geodynamics, 2010, 30(6): 100-104(张清华,隋立芬,牟忠凯.基于小波与ARMA模型的卫星钟差预报方法[J].大地测量与地球动力学,2010,30(6):100-104) |
| [13] | Wang Jigang. Research on Time Comparison Based on GPS Precise Point Positioning and Atomic Clock Prediction[D]. Beijing:Graduate School of CAS, 2010(王继刚.基于GPS精密单点定位的时间比对与钟差预报研究[D].北京:中国科学院研究生院,2010) |
| [14] | Lei Yu, Zhao Danning, Li Bian, et al. Prediction of Satellite Clock Bias Based on Wavelet Transform and Least Squares Support Vector Machines[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 815-819(雷雨,赵丹宁,李变,等.基于小波变换和最小二乘支持向量机的卫星钟差预报[J].武汉大学学报·信息科学版, 2014, 39(7): 815-819) |
| [15] | Wang Yupu, Lv Zhiping, Cui Yang, et al. Predicting Navigation Satellite Clock Bias Using Agenetic Wavelet Neural Network[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 809-814 (王宇谱,吕志平,崔阳,等.利用遗传小波神经网络预报导航卫星钟差[J].武汉大学学报·信息科学版, 2014, 39(7): 809-814) |
| [16] | Feng Suiliang.Study on the Methods of Data Preprocessing and Performance Analysis for Atomic Clocks[D]. Zhengzhou:Information Engineering University,2009 (冯遂亮.原子钟数据预处理与钟性能分析方法研究[D].郑州:信息工程大学,2009) |
 2016, Vol. 41
2016, Vol. 41



