文章信息
- 熊汉江, 李秀娟
- XIONG Hanjiang, LI Xiujuan
- 一种提取山脊线和山谷线的新方法
- A New Method to Extract Terrain Feature Lines
- 武汉大学学报·信息科学版, 2015, 40(4): 498-502
- Geomatics and Information Science of Wuhan University, 2015, 40(4): 498-502
- http://dx.doi.org/10.13203/j.whugis20140004
-
文章历史
- 收稿日期:2014-01-02
地形特征线是地貌图形的“骨架”。山脊线和山谷线作为非常重要的地形特征线,在制图综合、水文分析、地形重建、等高线自动综合等方面具有重要的意义。
基于规则格网DEM提取山脊线和山谷线的算法主要有基于图像处理技术的方法[1, 2]、基于地形表面几何形态分析的方法[3]以及基于形态分析和流水物理分析相结合的方法[4]等。该类方法大都基于栅格数据,抗噪性稍差,且特征点连接成线时较为困难。从精度和实用性来看,基于等高线数据的山脊、山谷线提取意义更大[5],主要方法有等高线曲率判别法[6]、垂距限差法[7]、等高线骨架化法[8]等。曲率判别法实现较为简单,但受阈值影响较大;垂距限差法中的代表性算法是Donglas-Peucker算法,该方法最先被应用于数据压缩,后被广泛用于特征提取、制图综合等多领域。等高线骨架线法大都利用Voronoi图,该方法比较适用于对称地形,且对离散点的密度有特定的要求。
Mean Shift概念最早由Fukunaga于1975年在一篇关于概率密度梯度函数估计的文章中提出来,即偏移的均值向量。基于等高线离散点的山脊、山谷线的追踪,类似Mean Shift,实质也是寻找最大概率流向上地形特征点的过程。本文提出了一种基于矢量等高线,以Mean Shift思路为全局步骤,以多因素流水模型为局部追踪依据,在提取特征点的同时完成山脊、山谷线追踪的方法。
1 等高线拓扑关系建立
等高线中隐含着大量的特征地形信息,山谷线、山脊线在等高线模型中表现为几何特征上的弯曲组合[6],提取它们,能为相邻弯曲组合上特征点的追踪打下基础。
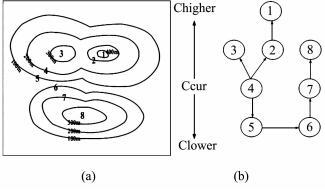
就图 1(a)的等高线建立如图 1(b)的拓扑关系。设当前的等高线为4号等高线,箭头代表等高线间的相邻性,同一行的等高线具有相同的高程值,自此往上高程增加,往下减小;以最低高程 等高线为基准,向上单向(无环)遍历组成一个自身等高线组,如{5、4、2、1}、{5、4、3}以及{6、7、8}分别为三个等高线组。依照此拓扑关系,可以方便地提取山顶和山麓等地形。
|
| 图 1 等高线拓扑关系图 Fig. 1 Topological Relations of Contour Lines |
等高线数据以近似凹包或凸包[9]的形式记录地形起伏。对于成组或整幅图的等高线,为保证整体凹凸弯曲的一致性,必须对初始数据进行预处理,使等高线坐标串行进方向一致。本文假定处理后所有等高线坐标串行进方向的左侧均为高。
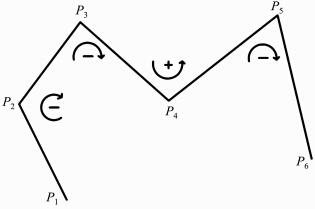
定义等高线点的拐角为以该点为交点的两相邻线段之间的夹角,如图 2所示,P2点的拐角即为线段P1 P2 与线段P2 P3之间的夹角。此处约定拐角为正的点凹凸属性为凸,拐角为负的点凹凸属性为凹。采用CCW(counter clock wise)规则来确定拐角的正负:若P1、P2、P3呈顺时针排列,则P2点的拐角为负;若P3、P4、P5呈逆时针排列,则P4点的拐角为正。
|
| 图 2 拐角正负计算 Fig. 2 The Calculation of Curvature’s Sign |
根据等高线坐标串走向的预处理规则和拐角正负的判定规则(CCW),拐角值为正的弯曲向等高线低值区凸起,拐角值为负的弯曲向等高线高值区凸起。结合山脊、山谷的属性,拐角为正的是山脊,拐角为负的是山谷。之后可考虑将点进行合并及分离,实现对等高线弯曲的分割,同时排除对弯曲影响不大的孤立点。
对于同一条等高线上的多个点,如果连续并且凹凸属性相同,则进行合并;若存在单点与两侧弯曲凹凸属性不一致且该点拐角较大,则该点为两弯曲分界点,若该点拐角较小,则视为抖动,合并两弯曲。
3 利用Mean Shift思路提取山脊线和山谷线
本文借鉴Mean Shift算子的思路,结合山脊、山谷的地形特性及其与等高线几何弯曲的对应性,对该算子进行一定的改变,将重心从聚类、分割转移到中心漂移点的追踪,即山脊、山谷特征点的提取及连接。具体步骤如下:① 根据山脊、山谷的分水、汇水性,将山顶、山麓等地形的特征点作为追踪的初始起点,后续遍历过程中所需的聚类中心根据等高线的弯曲特性实时提取;② 利用等高线几何弯曲上点的凹凸属性确定追踪区域的虚拟扇形;③ 依据流水模型,按“流向最大概率”原则确定期望流向,提取理想山脊或山谷特征点;④ 将新提取的理想特征点作为新的追踪中心;⑤ 重复步骤③~④,最终至山谷线汇集到河流主枝,山脊线追溯至山顶方向。
3.1 追踪起点确定
追踪起点主要分为初始追踪起点和后续追踪起点。初始追踪起点即为从山顶、山麓提取的特征点,后续追踪起点为遍历完当前等高线所有特征点后,在相邻等高线上提取的未被遍历过的特征点。
本文采用离散曲线演化(discrete curve evolution,DCE)算法来提取追踪起点。该算法在剔除噪声、获取最佳轮廓特征点方面有一定优越性[10, 11]。其中,两线段 Si∪Si+1公共点的重要性指数计算如下:
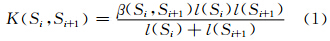
式中,β(Si,Si+1)表示Si 、Si+1组成的夹角;l(Si)、l(Si+1)分别为Si 、Si+1的长度。
式(1)原型来自曲率计算公式,且将两线段所在三角形的面积考虑在内[9, 10]。
根据DCE演化过程中点的删除顺序可标记点的重要性级别,在等高线弯曲分割的基础上,从每个需要提取追踪起点的弯曲上提取重要性最大的点作为追踪起点。
3.2 虚拟扇形追踪区域确定
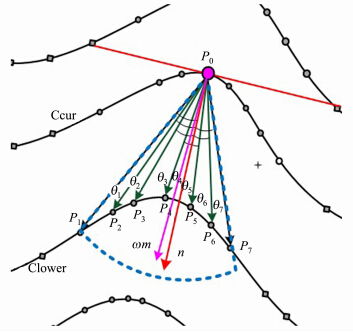
已标记点的凹凸属性中,水流分子只会沿示坡线下降的方向流向属性为凹的下游,即山谷区域,因此,本文采用虚拟扇形区域来建立追踪区域。如图 3蓝色虚线区域所示,该扇形充分考虑了等高线弯曲与山脊、山谷的对应性,将单根等高线上的特征点提取延伸至最相关的等高线点域。
图 3中,点P0为追踪起点,根据等高线间的拓扑关系,获取下一条等高线Clower并得到凹凸属性一致的最近点 P4,取 P4 附近连续相邻且凹凸属性一致的点 P1~P7,构成虚拟扇形区域,实现等高线弯曲局部同性质点的聚类分割。
|
| 图 3 多因素流水模型 Fig. 3 Multifactorial Falling Water Model |
Mean Shift算子在确定聚类区域和中心位置后,通过计算样本的平均位置来进行中心漂移,即假设在d维空间 Rd中的n个样本点为xi,i=1,……n,Sh是一个半径为h的高维球区域,wi 为向量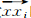 的权重,则x点的Mean Shift向量为:
的权重,则x点的Mean Shift向量为:
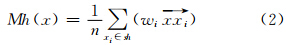
类似地,根据流水物理模拟分析,山谷点汇集至河流或谷底,山脊点向山顶追溯,偏移向量即为最大概率流向。
如图 3所示,水流分子从P0往下游流,点 P1~P7 分别为根据等高线形状确定的属性为凹的山谷点,向量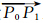 至向量
至向量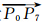 即为水流分子的可能流向,记为流水向量。在虚拟扇形追踪区域确定的基础上,建立流水模型:
即为水流分子的可能流向,记为流水向量。在虚拟扇形追踪区域确定的基础上,建立流水模型:
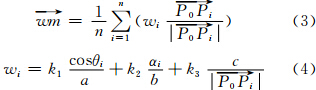
式中,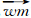 为求得的期望流向;
为求得的期望流向;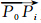 为该山谷弯曲中的第i个流水向量,i=1,…,n;wi 为流水向量
为该山谷弯曲中的第i个流水向量,i=1,…,n;wi 为流水向量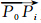 的总权重,包含3个影响因子cosθi、αi、
的总权重,包含3个影响因子cosθi、αi、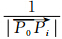 ,ki(0≤ki≤1,i = 1,2,3) 为3个影响因子的相对权重。实验取k1 = k2 = k3 = 1/3,也可根据等高线数据特征赋予不同值;θi为各流水向量与法向量的夹角,αi为根据DCE公式计算的P1~Pn点的重要性大小;a=max<cosθi>,b=max<αi>,c=min< |
,ki(0≤ki≤1,i = 1,2,3) 为3个影响因子的相对权重。实验取k1 = k2 = k3 = 1/3,也可根据等高线数据特征赋予不同值;θi为各流水向量与法向量的夹角,αi为根据DCE公式计算的P1~Pn点的重要性大小;a=max<cosθi>,b=max<αi>,c=min< |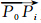 | >。
| >。
该模型的整体形式为期望,充分体现特征点在单个弯曲上趋向于采样平均;影响因子cosθi考虑了山脊线、山谷线垂直于等高线的特性;点的重要性大小αi说明特征点的提取趋向于对等高线弯曲形状贡献大的地形点,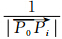 则体现水流方向沿坡度最大方向。
则体现水流方向沿坡度最大方向。
由式(3)~(4)可得图 3中期望流向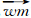 ,取与其夹角最小的
,取与其夹角最小的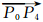 为最大概率流向,即P4为最终被提取的山谷特征点。由图 3可以看出,此点与目视解译相一致。通过此流水模型提取的山脊、山谷点更准确,最大概率流向与实际地形走向更相符。
为最大概率流向,即P4为最终被提取的山谷特征点。由图 3可以看出,此点与目视解译相一致。通过此流水模型提取的山脊、山谷点更准确,最大概率流向与实际地形走向更相符。
3.4 山脊、山谷特征点提取及连接
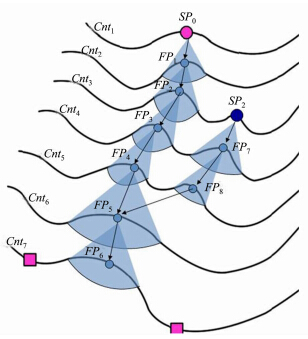
本文在对等高线预处理并计算地形点的凹凸性后,可将等高线弯曲进行分割,即属性为凸的点为山脊点,属性为凹的点为山谷点。然后根据多因素流水模型,按虚拟扇形区域,遵循“流向最大概率”原则寻找山脊点和山谷点,并同步建立前后连线关系。如图 4所示,以山谷线为例说明追踪过程。
|
| 图 4 山脊线和山谷线追踪过程 Fig. 4 Tracing Process of Ridge and Valley |
(1)从起始追踪起点SP0出发,向下寻找与其凹凸性一致的相邻等高线弯曲,建立虚拟扇形搜索区域,根据式(3)~(4)确定最大概率流向,找到特征点FP1;
(2)以点FP1为起点循环执行步骤(1),直到取不到下一条等高线,即追踪至FP6为止;
(3)递归至起始等高线Cnt1,若其所有弯曲都被遍历,则向下一等高线移动,直到发现未被遍历的弯曲,从该弯曲提取后续追踪起点,如点SP2,并将当前等高线Cnt3赋值给起始等高线;
(4)从后续追踪起点SP2出发,按步骤(1)~(3)执行。若下一个弯曲已被遍历,并提取出特征点,如点FP5,且FP7、FP8、FP5构成的夹角不小于120 °,直接将FP8连接至FP5;若夹角小于120 °,则找寻下一条等高线最邻近弯曲上的特征点,如点FP6;同理,夹角不小于120°直接连接,否则不连接。
4 实验结果与分析
通过与其他方法进行对比实验验证本文算法的正确性和有效性。实验中等高线组一组由4 538个点构成,最大高程为890 m,最小高程为610 m;另一组由8 012个点构成,最大高程为900 m,最小高程为480 m,等高距均为10 m。
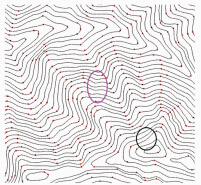
垂距限差法中较有代表性的是Douglas-Peucker算法,提取的特征点如图 5所示。从图 5中可以看出,该方法提取轮廓特征点的效果较好,但存在较平缓的山谷、山脊区域,容易遗漏此类弯曲上的特征点,如图 5绿色框中区域。且该算法需要合适的阈值控制,阈值过小,容易产生过多干扰特征;阈值较大,则容易遗漏小的细节分支,如图 5粉色框区域所示。
|
| 图 5 Douglas-Peucker 算法提取的特征点 Fig. 5 Feature Points Extracted by Douglas-Peucker Algorithm |
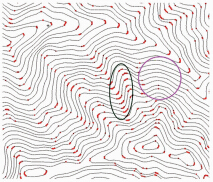
等高线曲率判别法仅从局部考虑,在弯曲明显的区域提取过多的特征点,如图 6绿色框区域,增加了后续连线的复杂性,而在等高线较为平缓的宽山脊或是U型谷区域,容易遗漏特征点,如图 6粉红色框区域。该方法同样受阈值影响较大,且某点曲率大小随用于计算的两侧点的不同而变化。
|
| 图 6 曲率判别法提取的特征点 Fig. 6 Feature Points Extracted by Curvature |
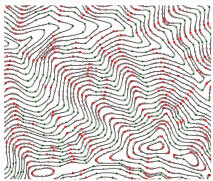
利用本文方法提取的地形特征点如图 7所示,该方法能同时提取出山脊、山谷特征点。绿色点和红色点分别代表弯曲分割后属性为凹和属性为凸的等高线点。从图 7中可以观察,属性为凹的点域能很好地对应实际地形中的山谷区域,属性为凸的点域则对应山脊区域。
|
| 图 7 本文方法提取的特征点 Fig. 7 Feature Points Extracted by the New Method |
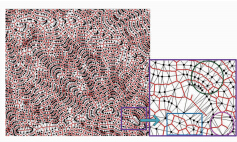
利用骨架线法提取地形特征线的效果如图 8所示。由图 8可知,该方法较适合对称地形的特征提取,能较好地提取等高线间横向的中轴线,但对纵向的山脊山谷线的提取不够理想,且受等高线点采样密度的影响较大。若等高线采样密度较低,则容易形成穿越等高线的骨架(如图 8蓝色框区域所示);对于弯曲明显时的山脊、山谷,能较好地提取特征线,如图 8粉红色框区域所示,否则,相邻等高线间构网的三角形较多,提取不到纵向的山脊、山谷线,如图 8绿色框区域所示。
|
| 图 8 骨架线法提取的特征线 Fig. 8 Feature Lines Extracted by Skeleton Method |
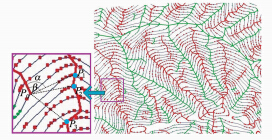
本文提取山脊、山谷线的效果如图 9、图 10所示,其中包含等高线弯曲分割、特征点提取及连接的结果。追踪起点的确定先从全局上进行DCE演化,后将缩放至单个弯曲,减少了弯曲遗漏特征点。其余特征点依流水模型提取并同时建立连线关系。山谷线在绿色山谷点域中提取,从山顶方向出发,向下追踪。从图 9、图 10可以看出,山谷线的追踪较为完整,且较好地体现了其“汇水”特性,与人工判读的结果一致;山脊线在红色山脊点域中提取并连接,与等高线的地形起伏保持较好的一致性,但在某些宽山脊区域存在缺陷,稍微破碎,如图 9中粉色框所示。根据本文的追踪算法,在特征线已连接至 P0,且其下一条等高线的最邻近弯曲已提取出特征点P1的基础上(如图 9粉色框区域),需判断夹角α是否不小于120°,若小于,则寻找下一条等高线最邻近弯曲上的P2点,若夹角β 仍小于阈值120°,则P0停止追踪。目视P0应被连接至P3,但需在无特征点过渡的情况下穿越多条等高线,在整体特征线连接的过程中容易产生错误。
|
| 图 9 本文方法提取的特征线 Fig. 9 Feature Lines Extracted by the New Method |

|
| 图 10 本文方法提取的较大区域的特征线 Fig. 10 Feature Lines Extracted of Bigger Area by the New Method |
山脊线和山谷线构成了地貌形态的基本骨架。自动提取山脊线和山谷线在制图综合、工程应用等多方面具有重要的意义。本文提出了一种以Mean Shift思路为全局步骤,以多因素流水模型为局部追踪依据来提取山脊线和山谷线的方法,该方法能充分考虑等高线间的拓扑关系,等高线弯曲与特征地形的对应性,将特征点的提取从单根等高线扩展到相邻等高线凹凸属性一致的点域。文章采用10m等高距的真实等高线数据进行了试验,试验结果表明该方法能增加特征提取的正确性、目的性,与人工识别具有较强的一致性,提取特征点的同时建立连线关系,减少了噪声干扰和传统后续特征点连线的复杂性。
| [1] | Band L E. Topographic Partition of Watersheds with Digital Elevation Models[J]. Water Resources Research, 1986, 22(1):15-24 |
| [2] | Kong Yueping, Fang Li, Jiang Yonglin, et al. A New Method of Extracting Terrain Feature Lines by Morphology[J]. Geomatics and Information Science of Wuhan University, 2012, 37(8):996-999(孔月萍, 方莉, 江永林, 等. 提取地形特征线的形态学新方法[J]. 武汉大学学报·信息科学版, 2012, 37(8):996-999) |
| [3] | Huang Peizhi, Liu Zehui. Extraction of Ridge and Valley from DEM Based on Gradient[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5):396-399(黄培之, 刘泽慧. 基于地形梯度方向的山脊线和山谷线的提取[J]. 武汉大学学报·信息科学版, 2005, 30(5):396-399) |
| [4] | Huang Peizhi. A New Method for Extracting Terrain Feature Lines from Digitized Terrain Data[J]. Geomatics and Information Science of Wuhan University, 2001, 26(3):247-252(黄培之. 提取山脊线和山谷线的一种新方法[J]. 武汉大学学报·信息科学版, 2001, 26(3):247-252) |
| [5] | Jin Hailiang, Kang Jianrong, Gao jingxiang. Research on the Algorithm of Extracting Ridge and Valley Lines Using Contour Data[J]. Geomatics and Information Science of Wuhan University, 2005, 30(9):809-812(靳海亮, 康建荣, 高井祥. 利用等高线数据提取山脊 (谷) 线算法研究[J]. 武汉大学学报·信息科学版, 2005, 30(9):809-812) |
| [6] | Fei Lifan. Experiments of Group-Generalization of Contour Lines on Topographic Maps[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1993, 18(Suppl):6-22(费立凡. 地形图等高线成组综合的试验[J]. 武汉测绘科技大学学报, 1993, 18(增刊):6-22) |
| [7] | Huang Lina, Fei Lifan. Experimental Investigation on the Three Dimension Generalization of Contour Lines using 3D D-P Algorithm[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1):55-58(黄丽娜, 费立凡. 采用3D D-P算法的等高线三维综合实验研究[J]. 武汉大学学报·信息科学版, 2010, 35(1):55-58) |
| [8] | Dakowicz M, Gold C. Extracting Meaningful Slopes from Terrain Contours[J]. International Journal of Computational Geometry & Applications, 2003, 13(04):339-357 |
| [9] | Basri R, Costa L, Geiger D, et al. Determining the Similarity of Deformable Shapes[J]. Vision Research, 1998, 38(15):2 365-2 385 |
| [10] | Bai X, Latecki L J, Liu W Y. Skeleton Pruning by Contour Partitioning with Discrete Curve Evolution[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2007, 29(3):449-462 |
 2015, Vol. 40
2015, Vol. 40



