文章信息
- 张清华, 隋立芬, 甘雨, 肖国锐, 戚国宾
- ZHANG Qinghua, SUI Lifen, GAN Yu, XIAO Guorui, QI Guobin
- WGS84与ITRS基准转换参数估计及长期演化特性分析
- Datum Transformation Parameters Estimation and Long-term Evolution Analysis of WGS84 and ITRS
- 武汉大学学报·信息科学版, 2015, 40(3): 395-400
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 395-400
- http://dx.doi.org/10.13203/j.whugis20130017
-
文章历史
- 收稿日期:2014-04-07
2. 地理信息工程国家重点实验室, 陕西 西安, 710054
2. State Key Laboratory of Geographic Information Engineering, Xi'an 710054, China
坐标基准是GNSS系统的重要组成部分,是描述物体空间位置和速度的客观基础[1]。GPS采用的坐标基准是WGS84,美国的国家大地测量局(National Geodetic Agency,NGA)就在此坐标系下进行轨道确定和时间同步等活动[2]。IGS作为一个公共服务机构,在ITRS框架下不断对GPS卫星的轨道和钟差进行估计,并且可以提供高精度钟差和轨道的产品,获得了广泛的应用[3]。研究表明[1],WGS84和ITRS的一致性达到5 cm,对大多数用户而言(精度低于5cm)不需要考虑两者之间的差异,但对精度有更高要求的用户以及科学研究的需求,估计两者之间的转换参数以及分析其变化特性是必要的。
美国的GPS系统已经成功运行多年,无论是NGA还是IGS求取的事后精密轨道精度近年来已经达到1~2 cm[1,2,3],这也为基于精密星历求取转换参数提供了数据基础。仅就坐标转换技术本身而言,国内外学者已有大量研究:针对点位分布不均匀的情况,可采取点位重心化算法[4];针对不同点位精度的差异,可采取加权最小二乘算法[5];针对个别点位含有粗差的情况,可采用基于抗差估计理论的算法[6];针对顾及设计矩阵误差的情况,可采取整体最小二乘的方法[7,8] ;针对传统的三维基准转换模型局限于求取小角度,文献[9]提出一种适用于大角度的三维坐标转换参数求解算法。实际应用中,在兼顾精度计算量的情况下,可根据所选数据情况采取合适的坐标转换方法。
对于长时间尺度上的转换参数序列,其中不可避免地存在一些粗差和噪声,为了从中分析其变化规律,首先对转换参数时间序列采取一定的处理。经验模分解(Empirical Mode Decomposition,EMD)是NASA的Huang提出的一种数据处理方法,其突出特点在于不依赖任何基函数,是一种数据驱动的自适应分析方法,与常用的小波分解法具有本质区别,可应用于多种类型信号的分解和降噪,其在卫星导航和惯性导航的消噪中获得广泛应用[10,11],本文拟采取EMD算法进行数据的消噪。在此基础上,采用经典谱分析方法来提取其周期项[12,13],这种方法在各个科学研究的背景下都有广泛的应用[14,15,16,17]。
文献[18]曾对ITRS和PZ-90的转换参数时间序列进行分析,并发现了平移参数的重要周期特性。我国的CGCS2000与ITRS和WGS84的兼容性可达到5 cm[19,20,21],但采用CGCS2000坐标基准的北斗导航系统各类卫星的精密星历的精度尚未能达到此量级,所以研究WGS84和ITRS的转化参数估计算法和演化特性也可为以后研究CGCS2000与WGS84和ITRS之间的关系提供一定参考。 1 基于精密星历的基准转换参数估计 1.1 基准转换参数估计算法
对于空间直角坐标系的转换,常用的7参数模型有布尔沙模型和莫罗金斯基模型,但对全球范围,布尔沙模型比较适合[22]。采取布尔沙模型进行坐标转换用的数据可以是地面点坐标,也可 以是卫星位置坐标(即精密星历或广播星历),两 者没有本质的差异。由于NGA和IGS都在不断地计算GPS卫星的精密星历,且具有较高精度,故本文采用精密星历来估计基准转换参数。下面对基于精密星历的布尔沙模型做简要介绍。
假设参与解算的GPS卫星共有 n个(1,…,n),第i颗卫星在WGS84下和ITRS下坐标分别为[X1i,Y1i,Z1i]T和[X2i,Y2i,Z2i]T,则它们之间具有如下关系:
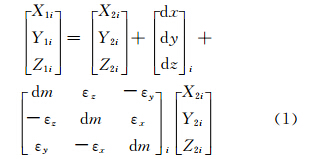
式中,dx、dy、dz为3个平移参数;εx、εy、εz为3个旋转参数;dm为尺度参数。对于n颗卫星而言,式(1)可以写成:
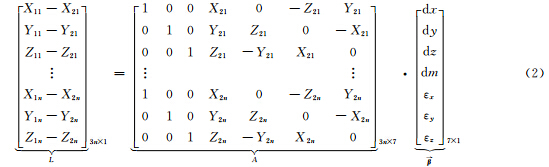
式(2)与n颗卫星联立求解转换参数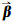 的方程,至少需要3个公共点,才可求取
的方程,至少需要3个公共点,才可求取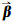 的值,如果n大于3,则需要解如下超定方程:
的值,如果n大于3,则需要解如下超定方程:
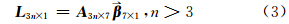
在最小二乘准则下,即VT PV =min,其中V=A3n×7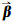 7×1-L3n×1,可求得
7×1-L3n×1,可求得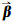 的平差解,P 为n个点坐标协方差矩阵的逆矩阵(即权阵)。 本文对星历坐标的协方差矩阵进行如下假设和简化:① 卫星的星历精度和钟的稳定性正相关;② 每颗卫星的坐标3个分量独立;③ 各个卫星之间的坐标独立。在以上的假设和简化下,P 为对角阵:
的平差解,P 为n个点坐标协方差矩阵的逆矩阵(即权阵)。 本文对星历坐标的协方差矩阵进行如下假设和简化:① 卫星的星历精度和钟的稳定性正相关;② 每颗卫星的坐标3个分量独立;③ 各个卫星之间的坐标独立。在以上的假设和简化下,P 为对角阵:
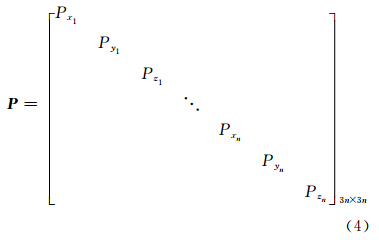
则由精密星历求得的转换WGS84和ITRS的转化参数为(LS解):
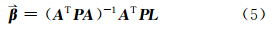
针对基于精密星历的基准转换参数估计,需要利用每天的精密星历计算出一组参数,而每天的在轨卫星在运行过程中,可能发生轨道机动、卫星维护和原子钟调相等问题,所以需要选取适当的卫星来进行参数估计,以避免不必要的干扰。另外,精密星历给出的时间间隔是2 h,即1 d可以给出12组参数,由于本文侧重于在1 000 d以上的尺度上分析参数的变化规律,所以每天只求取一个平均值,以代表当天最终的转换参数估计结果。在§2.1中假设卫星的星历精度和钟的稳定性正相关,那么在定权过程中,如果根据不断估计每天每个星载原子钟的稳定性,比较繁琐,本文考虑在一定的时间尺度上对所有的原子钟进行估计,并根据其量级进行定权。具体的基准转换参数计算流程见图 1。
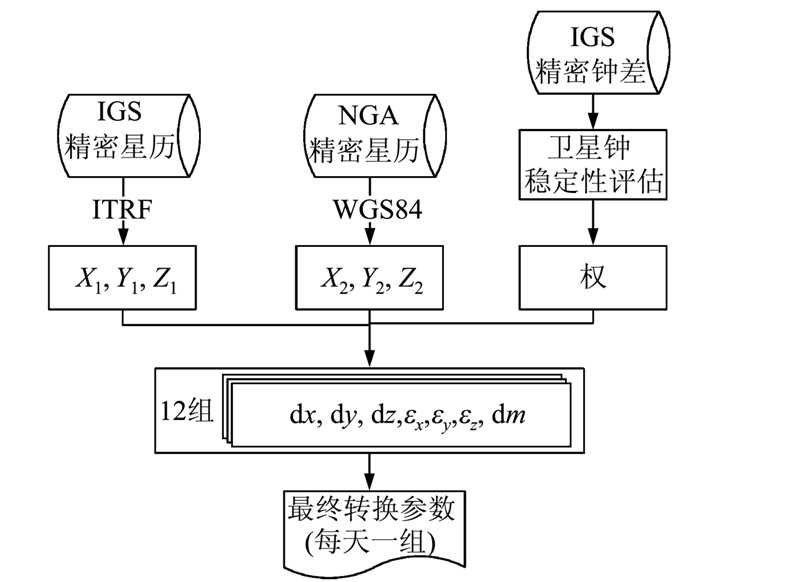 |
| 图 1 基准转换参数计算流程图Fig. 1 Coordinate Transformation Chart |
EMD可将复杂的信号分解成多个按频率排列的本征模态函数(Intrinsic Mode Decomposition,IMF)的和,这些IMF可以是非线性非平稳的,在对变化规律未知的时间序列进行消噪时具有非常明显的优势。Huang认为任何信号都是由若干个IMF相互重叠形成的复合信号,EMD分解的目的就是为了获取IMF。IMF须满足以下两个条件: ① 在整个时间序列范围内,局部极值点与过零点的数目相等;② 在任意时刻点,局部上包络线与下包络线必须为零。
对于基准转换参数的时间序列,首先要进行IMF分解,分解过程通过一个称为筛选(Sifting)的步骤来进行,其详细过程可参见文献[18]。完成筛选步骤后,基准转换参数的时间序列xi(7参数的某一个)可表示为:

由EMD的原理可知,分解得到的n个IMF的频率按先后顺序成几何级数递减,对于有噪声污染的转换参数时间序列,其先分解出的IMF通常含有高频噪声,若除去先分解的几个IMF,把其余的IMF组合起来形成一个信号,可以削弱噪声的影响。 2.2 经典谱分析算法
谱分析主要是利用数据形式呈波形的性质,通过对数据波形的幅值进行分析,找出数据序列中存在的显著周期项,这些周期项在谱图上表现为具有较大能量的特征。
坐标转换参数的时间序列数据的谱分析可表示为 (xi为7参数中的一个参数):
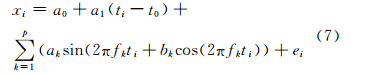
式中,a0+a1(ti-t0)旨在提取转换参数时间序列的线性趋势项;p为主要周期函数的数目;fk、Ak和φk为主要周期项对应的频率、振幅和相位;ej为谱分析的模型残差。谱分析模型是对多项式模型中的残差进行周期分析,是对多项式模型的改进。式(7)中的p、fk可由能量-频率图来分析得出。 3 算例分析 3.1 基准转换参数的估计
在算例分析中,采取IGS和NGA提供的2009-01-01~2012-06-30共1 306 d的精密星历,在§2.2中的算法流程下求得1 300组转换参数,结果见图 2,横坐标为时间,间隔为1 d,纵坐标为7个基准转换参数的值。表 1中给出2009~2012每年的转换参数平均值(2012年平均值为半年的数据得到)。
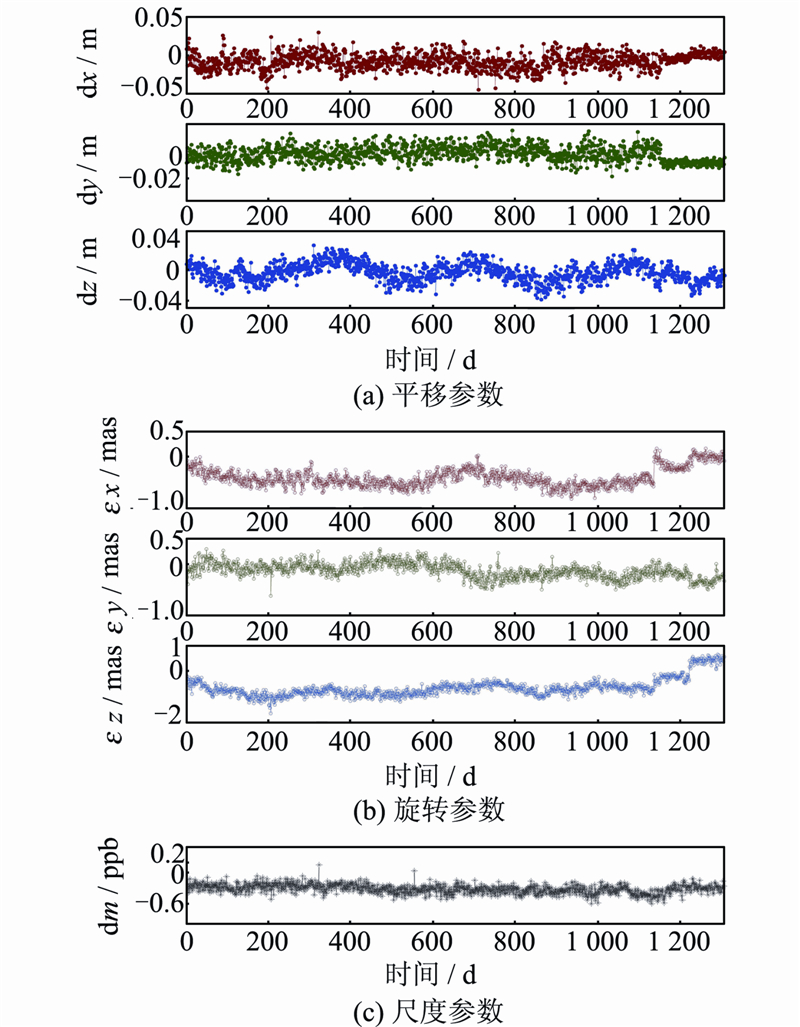 |
| 图 2 WGS84和ITRS的转换参数时间序列Fig. 2 Transformation Parameters of WGS84 and ITRS |
| 转换参数 | 年平均 | |||
| 2009 | 2010 | 2011 | 2012 | |
| dx/m | -0.006 | -0.008 | -0.009 | -0.004 |
| dy/m | 0.009 | 0.014 | 0.011 | 0.002 |
| dz/m | -0.002 | 0.001 | -0.005 | -0.009 |
| εx/mas | -0.401 | -0.482 | -0.512 | -0.088 |
| εy/mas | -0.055 | -0.046 | -0.033 | -0.197 |
| εz/mas | -0.825 | -0.801 | -0.721 | 0.043 |
| dm/ppb | -0.294 | -0.307 | -0.355 | -0.379 |
通过分析得出以下结论。
1) 3个平移参数的年平均数多数在mm级(除了dy在2010和2011年平均值达到cm级),而每天的平均值也都在5 cm之内;
2) 3个旋转参数的年平均数都在0.1 mas级,而每天的平均值都不会超过0.2 mas;
3) 尺度参数为负值,无论年平均值还是每天的平均值,都在0.1 ppb的量级;
4) 总体来说,利用星历法得到的WGS84和ITRS转换参数具有比较稳定的特性。 3.2 转换参数长期演化特性分析
由§3.1计算得到WGS84和ITRS转换参数的一组时间序列,在对其进行周期项分析之前,首先通过EMD进行去噪处理,为下一步的谱分析做准备。考虑到文章篇幅,这里仅对平移参数dx做去噪处理,其他参数的去噪与之相似,这里不再赘述,关于EMD分解的结果如图 3所示。
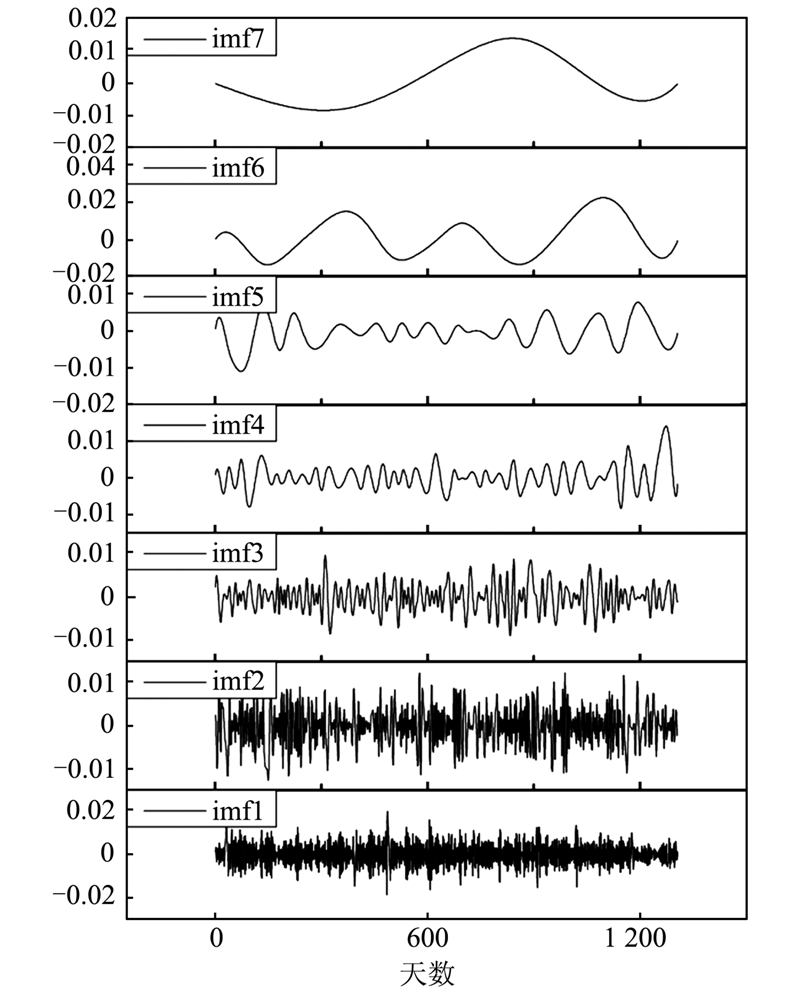 |
| 图 3 dx项时间序列的EMD分解结果Fig. 3 EMD Results of dx |
在图 3中,dx中所含的噪声信号集中于imf1~imf5中,而在imf6和imf7中可以明显地观测到周期项。通过去除这些高频噪声,则有利于下一步的周期特性分析。
在对WGS84和ITRS转换参数经过EMD去噪处理后,对其进行谱分析,可以得到如下结果。
对于参数dx,经过FFT变换可得到结果,由图 4可知,dx的时间序列中具有两个明显的周期项,周期分别是T1=1/f1=1 282 d和T1=1/f1=345 d(精确到天)。类似地,求出其他6个参数的周期项,见表 2。
 |
| 图 4 dx项的FFT变换结果Fig. 4 FFT Results of dx |
| 参数 | 频率(Hz/86 400) | 主要周期/d |
| dx /m | f1=0.000 78 | T1=1 282 |
| f2=0.002 90 | T2=345 | |
| dy/m | f1=0.000 78 | T1=1 282 |
| f2=0.001 45 | T2=690 | |
| dz/m | f1=0.002 90 | T1=345 |
| f2=0.000 78 | T2=1 282 | |
| εx/mas | f1=0.000 77 | T1=1 299 |
| f2=0.002 18 | T2=459 | |
| εy/mas | f1=0.000 77 | T1=1 299 |
| f2=0.005 81 | T2=172 | |
| εz/mas | f1=0.000 77 | T1=1 299 |
| f2=0.002 18 | T2=459 | |
| dm/ppb | f1=0.000 77 | T1=1 299 |
通过分析以上图表可以发现:
1) 利用经验模分解(EMD)可以很好地去除高频噪声,进而得到参数时间序列的周期部分;
2) 在7个参数的周期项中,都存在一个约1 300 d的周期,这也就是整个参与基准转换参数估计的天数,从本质上来说,并不是一个严格意义上的周期项。
3) 在3个平移参数中,存在着另外3个周期项,分别是345 d,690 d和345 d,可以发现690 d刚好是345 d的2倍,这3个周期项是平移参数严格意义上的周期项;
4) 在3个旋转参数中,同样存在着另外3个周期项,分别是459 d,172 d和459 d这3个周期项是旋转参数严格意义上的周期项; 5) 对于尺度参数,不存在其他周期项,即不存在严格意义上的周期项。 4 结 语
本文针对WGS84和ITRS坐标基准之间的转换参数,利用由NGA和IGS提供的两个坐标基准下的GPS精密星历,采用7参数布尔沙模型来估计这些转换参数,并且对转换参数的时间序列的演化特性进行了分析,其中采用EMD的方法来进行去噪,并用经典谱分析来进行周期项分析,得到了一些有益的结论。
| [1] | Jiao Wenhai. Research on the Establishment of Satellite Navigation System Coordinates[R]. Shanghai Astronomical Observatory, Chinese Academy of Postdoctoral Work Report, 2003(焦文海.卫星导航系统坐标基准建立问题的研究[R].中国科学院上海天文台博士后工作报告, 上海天文台, 2003) |
| [2] | Kaplan E D. Understanding GPS:Principles and Application(Second Edition)[M].Norwood, MA:Artech House Publisher, 2006 |
| [3] | IGS Central Bureau. International GNSS Service Technical Report 2011[R]. IGS Central Bureau, 2012 |
| [4] | Chen Yu, Bai Zhengdong, Luo Teng.An Improved Bursa Model For Coordinate Transfomation[J].Journal of Geodesy and Geodynamics, 2010, 30(3):71-74(陈宇, 白征东, 罗腾.基于改进的布尔沙模型的坐标转换方法[J].大地测量与地球动力学, 2010, 30(3):71-74) |
| [5] | Lu Jue, Chen Yi, Zheng Bo, Application of Weighted Total Least Squares in ITRF Transformation[J].Journal of Geodesy and Geodynamics, 2011, 31(4):84-89(陆珏, 陈义, 郑波.加权总体最小二乘方法在ITRS转换中的应用[J].大地测量与地球动力学, 2011, 31(4):84-89) |
| [6] | Yang Y. Robust Estimation of Geodetic Datum Transformation[J].J Geod, 1999, 73:268-274 |
| [7] | Shen Y Z, Chen Y, Zheng D H. A Quaternion-based Geodetic Datum Transformation Algorith[J].J Geod, 2006, 80:233-239 |
| [8] | Ge Xuming, Wu Jicang.Iterative Method of Weight Constraint Total Least-Squares for Three-Dimensional Datum Transformation[J].Geomatics and Information Science of Wuhan University, 2012, 37(2):178-182(葛旭明, 伍吉仓. 三维基准转换的约束加权混合整体最小二乘的迭代解法[J].武汉大学学报·信息科学版, 2012, 37(2):178-182) |
| [9] | Yao Yibin, Huang Chengmeng, Li Chengchun, et al.A New Algorithm for Solution of Transformation Parameters of Big Rotation Angle's 3D Coordinate[J].Geomatics and Information Science of Wuhan University, 2012, 37(3):253-257(姚宜斌, 黄承猛, 李程春, 等.一种适用于大角度的三维坐标转换参数求解算法[J].武汉大学学报·信息科学版, 2012, 37(3):253-257) |
| [10] | Dai Wujiao, Ding Xiaoli, Zhu Jianjun, et al. EMD Filter Method and Its Application in GPS Multipath [J] .Acta Geodaetica et Cartographica Sinica, 2006, 35(11):321-327(戴吾蛟, 丁晓利, 朱建军, 等.基于经验模式分解的滤波消噪法及其在GPS多路径效应中的应用[J].测绘学报, 2006, 35(11):321-327) |
| [11] | Gan Yu, Sui Lifen. De-noising Method for Gyro Signal Based on EMD[J].Acta Geodaetica et Cartographica Sinica, 2011, 40(6):746-751(甘雨, 隋立芬. 基于经验模分解的陀螺信号消噪[J].测绘学报, 2011, 40(6):746-751) |
| [12] | Proakis J G. Digital Signal Processing Principles[M].4th Edition. Beijing:Electronic Industry Press, 2008 |
| [13] | Stoica P, Moses R L. Spectral Analysis of Signals[M].Beijing:Electronic Industry Press, 2012(彼得·斯托伊卡, 伦道夫·摩西.现代信号谱分析[M].吴仁彪, 韩萍, 冯青, 译.北京:电子工业出版社, 2012) |
| [14] | Guo Hairong, Yang Yuanxi, Jiao Wenhai. Robust Spectral Analysis on Time Series of Geocenter Motion[J].Acta Geodaetica et Cartographica Sinica, 2003, 32(4):308-312(郭海荣, 杨元喜, 焦文海.地心运动时间序列的抗差谱分析[J].测绘学报, 2003, 32(4):308-312) |
| [15] | Huang Guanwen, Zhang Qin, Xu Guochang, et al. IGS Precise Satellite Clock Model Fitting and Its Precision by Using Spectral Analysis Method[J].Geomatics and Information Science of Wuhan University, 2008, 33(5):496-499(黄观文, 张勤, 许国昌, 等.基于频谱分析的IGS精密星历卫星钟差精度分析研究[J].武汉大学学报·信息科学版, 2008, 33(5):496-499) |
| [16] | Zhang Bin, Ou Jikun, Yuan Yunbin, et al. Fitting Method for GPS Satellite Clock Errors Using Wavelet and Spectrum Analysis[J].Geomatics and Information Science of Wuhan University, 2007, 32(8):715-718(张斌, 欧吉坤, 袁运斌, 等.一种小波与谱分析结合的GPS精密卫星钟差拟合方法研究[J].武汉大学学报·信息科学版, 2007, 32(8):715-718) |
| [17] | Zhang Hong, Xie Na. Beijing Real Estate Market Cycle Analysis Based on Principle Componential and Spectral Analyses[J].Journal of Tsinghua University(Science and Technology), 2008, 48(9):58-60(张红, 谢娜.基于主成分分析与谱分析的房地产市场周期研究[J].清华大学学报(自然科学版), 2008, 48(9):58-60) |
| [18] | Jiao Wenhai, Wei Ziqing, Liu Guangming. Spectrum Analysis of Transformation Paramaters Between PZ-90 GLONASS and ITRF[J].Geomatics and Information Science of Wuhan University, 2003, 28(6):740-744(焦文海, 魏子卿, 刘光明, 等.PZ-90 GLONASS与ITRS之问转换参数的谱分析[J].武汉大学学报·信息科学版, 2003, 28(6):740-744) |
| [19] | Chen Junyong, Yang Yuanxi, Wang Min. Establishment of 2000 National Geodetic Control Network of China and It's Technological Progress[J].Acta Geodaetica et Cartographica Sinica, 2007, 36(1):1-8(陈俊勇, 杨元喜, 王敏, 等.2000国家大地控制网的构建和它的技术进步[J].测绘学报, 2007, 36(1):1-8) |
| [20] | Wei Ziqing, Liu Guangming, Wu Fumei. China Geodetic Coordinate System 2000:VelocityField in Mainland China[J].Acta Geodaetica et Cartographica Sinica, 2011, 40(4):403-410(魏子卿, 刘光明, 吴富梅.2000中国大地坐标系:中国大陆速度场[J].测绘学报, 2011, 40(4):403-410) |
| [21] | Wei Ziqing. China Geodetic CoordinationSystem 2000 and Its Comparision with WGS84[J].Journal of Geodesy and Geodynamics, 2008, 28(5):1-6(魏子卿.2000中国大地坐标系及其与WGS84的比较[J].大地测量与地球动力学, 2008, 28(5):1-6) |
| [22] | Zhuoligetu, Zhang Aihua. The Coordinate Transformation Between GPS and GLONASS[J].Crustal Deformation and Earthquake, 2000, 20(2):24-29(卓力格图, 张爱华.GPS与GLONASS的坐标转换[J].地壳形变与地震, 2000, 20(2):24-29) |
 2015, Vol. 40
2015, Vol. 40


