文章信息
- 付仲良, 赵星源, 王楠, 杨元维, 田宗舜, 俞志强
- FU Zhongliang, ZHAO Xingyuan, WANG Nan, YANG Yuanwei, TIAN Zongshun, YU Zhiqiang
- 一种基于流形学习的空间数据划分方法
- Spatial Data Partitioning Method Based on Manifold Learning
- 武汉大学学报·信息科学版, 2015, 40(10): 1294-1298,1323
- Geomatics and Information Science of Wuhan University, 2015, 40(10): 1294-1298,1323
- http://dx.doi.org/10.13203/j.whugis20141008
-
文章历史
- 收稿日期: 2014-12-30

2. 中国科学院遥感与数字地球研究所, 北京, 100094;
3. 浙江省地理信息中心, 浙江 杭州, 310012
2. Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100094, China;
3. Geographic Information Center of Zhejiang Province, Hangzhou 310012, China
空间连接(spatial join)操作是空间数据库系统中最重要的一个操作,即从两个数据集中获取满足一定空间谓词(如相交、覆盖等)的空间对象[1]。对于大数据量的空间数据,直接进行空间连接操作需要耗费的资源较大,这是因为直接对大数据量的空间数据进行网络传输时需要耗费较高的网络带宽,同时空间数据结构复杂,进行空间连接时涉及到复杂的图形操作,需要的运算开销较大[2]。空间数据划分能够有效地解决这一问题,它通过将待连接的两份数据进行划分,可以对划分结果分别进行连接操作,从而降低系统负载,提高空间连接效率。由此可见,数据划分是大数据量空间数据连接的前提和基础。为了保证空间连接查询的效率,要求空间数据划分结果尽量保持较低的冗余度和较高的数据均衡度[3]。
现有的数据划分方法主要包括空间填充曲线划分方法[4]、空间位置范围划分方法[5]、聚类划分方法[6]、空间索引划分方法[7]等。基于空间填充曲线进行空间数据划分主要是运用空间填充曲线将空间地物进行编码,根据编码值构建划分策略进行数据划分;基于空间位置范围进行数据划分是根据空间对象位置将空间范围划分成大小相等 或不等的网格进行划分;聚类划分方法的基本思 想是:选取聚类中心,按照最邻近距离、相似性等原则,通过反复迭代运算使目标函数收敛,得到最终聚类结果;空间索引划分方法是基于地物形态或某类空间分割原则(如R-Tree)实现空间划分。
然而,上述方法用于空间连接查询时存在着一些问题,如空间填充曲线在压缩映射时会损失空间数据的部分几何特性,在个别位置会出现较大的偏差,在进行空间连接时会降低运算效率,并且划分结果的冗余度较大;基于空间位置范围进行数据划分仅仅在X轴或Y轴方向上强制划分,可能会产生数据倾斜;空间聚类划分方法需要指定聚类数目或聚类中心,并且对随机均匀分布的空间数据适用性不强;空间索引划分方法的复杂度较高,当数据量比较大时,索引建立的时间较长,当空间数据动态变化时,需要反复建立索引,影响整体效率。
综上所述,目前的空间数据划分方法难以保持低冗余度和高数据量均衡度以及高效支持空间连接,针对这一问题,本文提出了一种基于流形学习的空间数据划分方法,使得划分结果能够充分满足空间连接操作对数据划分低冗余度和高数据量均衡度的需求。
1 流形学习ISOMAP算法原理多维尺度分析(multi-dimensional scaling,MDS)[8]和等距映射( isometric mapping,ISOMAP)[9]是流形学习中的经典方法。MDS是一种寻求保持数据点之间差异性(相似性)的线性降维方法,其基本思想是:高维空间距离远的点在低维嵌入空间中仍然远离;高维空间中相邻的点在低维空间中仍然相邻。对于空间数据的I个对象,定义一个距离函数的集合,其中δi,j是第i个和第j个对象之间的距离。于是有:
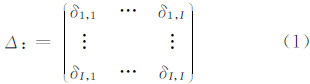
根据Δ,寻找I个向量 x1,…,x I∈ R N,使‖ x i- x j‖≈δi,j,且i,j∈I,其中‖·‖为向量的范数。通过最小化目标函数求解,
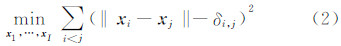
ISOMAP在MDS算法的基础上进行了改进,对于流形上所有的点,ISOMAP用它们之间的测地线距离代替欧氏距离。
流形学习作为一种新的非监督学习方法,近年来得到了广泛的关注和研究。如今,流形学习被应用于多个学科领域[9, 10, 11],但是,空间数据划分领域尚未引入流形学习的相关概念。而流形学习作为一种维数约简的方法,由于其保留了源数据几何结构不变性方面的特有优势,可以对空间数据进行“无损”降维,为空间数据划分提供了良好的基础。
2 基于流形学习的数据分割假设对空间数据集R进行数据划分,目标划分为N份,为了避免划分产生数据倾斜(data skew),需要进行网格分片预处理[12],即通过建立n×n的网格将R分割到不同的网格分片中(n×n》N)。需要注意的是,不同的分片中可能会含有相同的空间要素(ID相同的空间对象)。在网格分片预处理的基础上,本文提出了一种基于流形学习的空间数据划分方法。
2.1 网格编码分片预处理得到的n×n个网格可以看做是边长为n的正方形中的n×n个点,每个分片的坐标可用此正方形中点的坐标来表示,最终得到一个n2×2的坐标矩阵 M ,利用ISOMAP对坐标矩阵 M 进行降维处理,得到一维数组S=(S1,S2,…,Sn2),此即为网格分片的流形学习编码值。由于流形学习具备保留源数据几何结构不变性的优势,因此,网格分片的流形学习编码值S之间的差异反映了其在空间结构中距离远近的差异,编码值相差较大的两个分片在空间上距离较远,相差较小的两个分片在空间上距离较近。
2.2 网格映射编码完成后,需要按照编码值将n×n个分片映射到数据块中,本文提出了一种新的映射方式,其基本思想是:按照流形学习编码值将包含数据量较大的分片和其距离较近的分片映射到一个数据块中,以减少数据冗余,当各数据块包含的数据量达到阈值(未产生冗余数据且平均划分源数据时各数据块包含的数据量)时,将剩余网格分片依次映射到当前包含空间数据最少的数据块中,以提高划分结果的数据量均衡性。
算法中设计的变量为: N为待划分数据块的份数;i为当前正在映射的块;fi为第i个块中包含的要素的数量;M为数据集中包含要素的总量;sseed为当前正在映射的分片的编码值;S[]为网格分片的编码数组;m′为理想状态下完全不产生数据冗余时每个块包含的要素的数量。算法步骤如下:
1) 初始化i=0,m′= 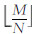 ;
;
2) 遍历S[],找到包含要素最多的分片,将其映射到第i个块中,获得其网格编码,记录为sseed;
3) 比较i与N,当i≥N时,跳转到第5)步;
4) 比较fi与m′,当fi≥m′时,i++,剩余要素向下一个块中进行映射,从S[]中移除sseed的记录,继续执行第2)步,开始对新的块映射;当fi < m′时,从S[]中查找与其差值最小的编码值,将编码值对应的分片映射到第i个块中,并消除冗余数据(ID相同的空间对象),从S[]中移除sseed的记录,将新得到的编码值记录为sseed,返回第3)步;
5) 对S[]中的分片按顺序进行映射,映射规则是将每个分片映射到当前包含数据量最少的数据块中,直到所有分片映射完为止。
3 实验分析 3.1 对比方法和实验数据介绍采用文献[2, 3]中的数据划分方法进行实验比较,两者分别通过线性编码和空间填充曲线编码的方式对网格划分的分片进行编码,然后通过轮转循环的方式映射到数据块中。
本文选用美国统计局TIGER/Line数据中2014年加利福尼亚州的街区数据(http://www.census.gov/geo/maps-data/data/tiger.html)作为实验数据。数据格式为Shape格式,包含630 686个面要素,大小为657 MB,在地图上的分布情况如图 1所示。

|
| 图 1 2014年加利福尼亚州街区分布情况图 Fig. 1 Blocks Distribution of California in 2014 |
将数据进行网格映射划分时,由于同一个空间对象可能被划分到多个分片中,因此,最终的划分结果可能会产生数据冗余,这会影响到系统的分析处理和数据传输效率,本实验将划分结果的冗余度作为第一个评价指标;数据量均衡度对于系统的负载均衡具有较大的影响,将其作为另一个评价指标。
1) 冗余度度量
设 M为源数据集包含数据的数量,N为数据划分的块数目,mi为第i个数据块中的数据量,R为划分结果的冗余度,则有:
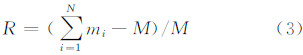
R越大,表明系统的冗余度越高,对于数据传输和运算效率的影响也越大。
2) 数据量均衡度度量
采用数据量离散度来衡量划分结果的数据量均衡度。数据量离散度采用标准差的公式来进行计算:
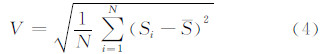
V值越大,表明数据块之间的数据量离散程度越高,均衡度越低,系统负载平衡性越低。
3.3 实验过程按照网格划分大小的不同,将实验分成A、B、C、D四组进行,其中,A、B、C、D 四组实验分别采用16×16、32×32、64×64、128×128的网格对数据进行分片。在四组实验中,按照划分数据块数目的不同,每组实验又分为a、b两类,其中,a类为划分为4份数据块时的情况,b类为划分为8类数据块时的情况。
表 1、表 2分别是当划分数据块份数为4份和8份时,4组实验中通过三种不同的划分方法得到的划分结果内各数据块数据量的比较情况。
| 数据块 | A组实验 | B组实验 | C组实验 | D 组实验 | ||||||||
| 线性编码轮转法 | 空间填充轮转法 | 本文方法 | 线性编码轮转法 | 空间填充轮转法 | 本文方法 | 线性编码轮转法 | 空间填充轮转法 | 本文方法 | 线性编码轮转法 | 空间填充轮转法 | 本文方法 | |
| Part1 | 133 840 | 103 971 | 160 740 | 149 568 | 153 761 | 160 892 | 161 772 | 169 169 | 159 757 | 165 190 | 182 456 | 159 748 |
| Part2 | 171 750 | 151 269 | 159 286 | 128 757 | 168 559 | 158 654 | 178 786 | 168 802 | 159 437 | 169 089 | 186 048 | 159 748 |
| Part3 | 141 352 | 182 692 | 169 099 | 184 548 | 164 191 | 161 541 | 160 471 | 166 927 | 158 577 | 167 095 | 181 290 | 159 748 |
| Part4 | 189 609 | 203 473 | 146 752 | 180 013 | 166 511 | 155 970 | 154 288 | 171 957 | 160 062 | 178 155 | 172 418 | 159 747 |
| 数据块 | A组实验 | B组实验 | C组实验 | D组实验 | ||||||||
| 线性编码轮转法 | 空间填充轮转法 | 本文方法 | 线性编码轮转法 | 空间填充轮转法 | 本文方法 | 线性编码轮转法 | 空间填充轮转法 | 本文方法 | 线性编码轮转法 | 空间填充轮转法 | 本文方法 | |
| Part1 | 45 545 | 43 520 | 80 987 | 69 763 | 90 083 | 80 052 | 80 054 | 79 035 | 79 963 | 79 232 | 91 084 | 80 484 |
| Part2 | 113 373 | 65 059 | 80 362 | 65 628 | 66 060 | 79 877 | 72 561 | 77 122 | 84 319 | 88 441 | 92 532 | 80 484 |
| Part3 | 98 690 | 101 301 | 78 888 | 73 257 | 72 446 | 79 876 | 67 195 | 84 680 | 79 972 | 86 670 | 93 020 | 80 484 |
| Part4 | 153 299 | 62 131 | 80 405 | 100 186 | 63 530 | 80 439 | 64 410 | 90 114 | 80 576 | 98 519 | 86 678 | 80 483 |
| Part5 | 88 295 | 60 483 | 83 032 | 79 805 | 63 821 | 81 592 | 81 721 | 90 705 | 79 963 | 85 995 | 93 749 | 80 482 |
| Part6 | 58 377 | 86 244 | 81 509 | 63 129 | 102 639 | 79 876 | 106 227 | 92 249 | 79 969 | 80 696 | 95 822 | 80 483 |
| Part7 | 42 662 | 81 422 | 82 748 | 111 291 | 91 895 | 81 002 | 93 278 | 82 785 | 79 969 | 80 472 | 90 563 | 80 482 |
| Part8 | 36 310 | 141 371 | 68 504 | 79 827 | 103 120 | 80 119 | 89 879 | 82 428 | 79 970 | 79 683 | 88 077 | 80 484 |
通过式(3)和式(4)可计算得到4组实验划分结果的数据冗余度和数据量离散度,具体结果见表 3、表 4。
| 实验方法 | A组试验 | B组试验 | C组试验 | D组试验 | ||||
| 4份 | 8份 | 4份 | 8份 | 4份 | 8份 | 4份 | 8份 | |
| 线性编码轮转法 | 0.93 | 0.93 | 1.93 | 1.93 | 3.91 | 3.91 | 7.74 | 7.77 |
| 空间填充轮转法 | 1.70 | 1.72 | 3.54 | 3.63 | 7.32 | 7.68 | 14.51 | 15.99 |
| 本文方法 | 0.82 | 0.91 | 1.01 | 1.93 | 1.13 | 2.22 | 1.32 | 2.09 |
| 实验方法 | A组试验 | B组试验 | C组试验 | D组试验 | ||||
| 4份 | 8份 | 4份 | 8份 | 4份 | 8份 | 4份 | 8份 | |
| 线性编码轮转法 | 22 604.6 | 38 504.5 | 22 836.3 | 15 918.1 | 9 086.4 | 13 218.0 | 4 971.3 | 6 112.9 |
| 空间填充轮转法 | 37 482.7 | 28 537.5 | 5 695.31 | 16 013.8 | 1 797.7 | 5 249.0 | 5 013.4 | 2 808.6 |
| 本文方法 | 7 986.1 | 4 360.3 | 2 182.8 | 590.6 | 554.7 | 1 424.3 | 0.4 | 0.8 |
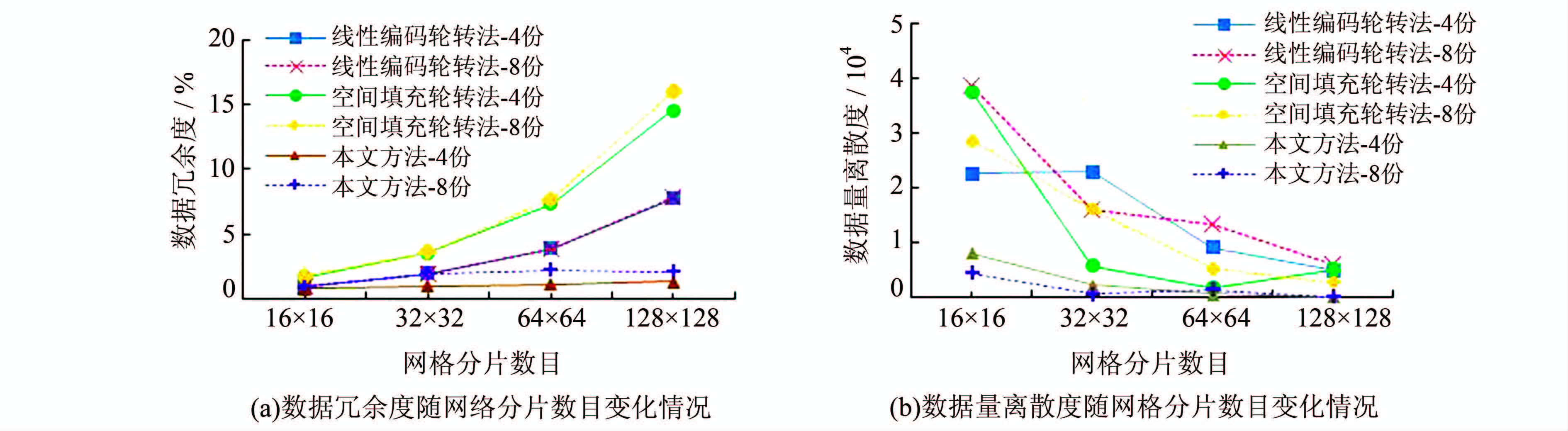
将A、B、C、D四组实验的结果进行统计,如图 2所示。
|
| 图 2 数据冗余度和数据量离散度随网格分片数目变化图 Fig. 2 Variation of Data Redundancy and Data Dispersion with Different Grid Subdivision Size |
从图 2(a)可以看出,对于A、B、C、D四组实验,随着网格分片数目的增加,三种划分方法的数据冗余度均有所增加,这是因为随着分片数的增加,网格中每个分片单元的面积逐渐减小,同一空间对象可能被划分到更多的分片中,产生的冗余数据也更多,同时,对于同一划分方法而言,数据划分的份数越多,划分结果的数据冗余度也越高,这是因为随着划分份数的增加,网格分片将会映射到更多的数据块中,这减弱了映射时对不同网格分片中冗余数据的去除效果。
从图 2(b)可以看出,对于A、B、C、D四组实验,随着网格分片数目的增加,三种划分方法的数据量离散度的变化趋势均为由高到低,这是因为随着分片数的增加,网格对于空间的分割更为“彻底”,对空间对象密集区域的分割也更加“充分”,因空间数据分布不均而产生的数据倾斜情况被大大降低。
对比分析图 2(a)和图 2(b)可以看出,相同条件下,空间填充轮转划分方法相较于线性编码轮转划分方法具有更高的数据量均衡度,但是数据冗余度较高,这是因为采用空间填充曲线进行编码,相较于线性编码,编码值相近的分片在空间上距离较近,这使得相近的分片被平均地映射到不同的数据块中,所以得到的结果的数据量均衡性较高,但由于是将相近分片映射到不同的数据块中,因此对冗余数据消除的效果较差,结果的数据冗余性较高。
由图 2可以看出,本文方法相较于其他两种划分方法,具有极低的数据冗余度和良好的数据量平衡度,这是因为:首先,划分方法使用流形学习算法进行分片编码时,可以充分保留分片数据的几何结构,映射方法通过流形学习编码值将空间距离较近的分片映射到相同的数据块中,有效减少了冗余数据的产生;其次,映射方法在映射时对数据块容量进行了控制,先使得所有的数据块包含的数据量达到理想容量(不产生冗余数据时数据量的平均值),之后将剩余的网格分片依次映射到当前包含数据量最少的数据块中,从而提高划分结果的数据量均衡性。
4 结语空间数据划分是提高空间连接效率的前提和基础。与已有的空间数据划分方法相比,本文基于流形学习算法的空间数据划分方法能够充分利用空间地物的内在几何特性,将邻近地物划分到同一数据块,以减少数据冗余,同时通过映射控制提高划分结果的数据量均衡性。实验表明,本文划分方法具有良好的实用性和可靠性,对于空间连接操作具有重要意义。
| [1] | Zhou X, Abel D J, Truffet D. Data Partitioning for Parallel Satial Join Pocessing[J]. Geoinformatica, 1998, 2(2): 175-204 |
| [2] | Patel J M, De Witt D J. Partition Based Spatial-merge Join[C].ACM SIGMOD Int Conf on Management of Data, New York, USA, 1996 |
| [3] | Zhang S, Han J, Liu Z, et al.SJMR: Parallelizing Spatial Join with Mapreduce on Clusters[C]//IEEE International Conference on Cluster Computing and Workshops. New Orleans, LA: IEEE Press, 2009: 1-8 |
| [4] | Wang Yongjie, Meng Lingkui, Zhao Chunyu. Spatial Partitioning of Massive Data Based on Hilbert Spatial Ordering Code[J]. Geomatics and Information Science of Wuhan University, 2007, 32(7): 650-653(王永杰, 孟令奎, 赵春宇. 基于 Hilbert 空间排列码的海量空间数据划分算法研究[J]. 武汉大学学报·信息科学版, 2007, 32(7): 650-653) |
| [5] | Abugov D. Oracle Spatial Partitioning: Best Practices (an Oracle White Paper)[R]. Oracle Inc, Redwood Shores, CA, 2004 |
| [6] | Guo D. Regionalization with Dynamically Constrained Agglomerative Clustering and Partitioning (REDCAP)[J]. International Journal of Geographical Information Science, 2008, 22(7): 801-823 |
| [7] | Cheng Changxiu. A Multi-scale Spatial Index Method[J]. Geomatics and Information Science of Wuhan University, 2009, 34(5): 597-601(程昌秀. 矢量数据多尺度空间索引方法的研究[J]. 武汉大学学报·信息科学版, 2009, 34(5): 597-601) |
| [8] | Borg I, Groenen P J F. Modern Multidimensional Scaling: Theory and Applications[M]. New York:Springer, 2005 |
| [9] | Sun Weiwei, Liu Chun, Shi Beiqi, et al. Low-dimension Manifold Feature Extraction of Hyperspectral Imagery Using Dimension Reduction with ISOMAP[J]. Geomatics and Information Science of Wuhan University, 2013, 38(6): 642-647(孙伟伟, 刘春, 施蓓琦, 等. 等距映射降维用于高光谱影像低维流形特征提取[J]. 武汉大学学报·信息科学版, 2013, 38(6): 642-647) |
| [10] | Xiong Wei, Zhang Lefei, Du Bo. A Multilinear Discriminant Subspace Projection with Orthogonalization for Face Recognition[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 583-587(熊维, 张乐飞, 杜博. 一种基于多维正交判别子空间投影的人脸识别方法[J]. 武汉大学学报·信息科学版, 2015, 40(5): 583-587) |
| [11] | Du Peijun, Wang Xiaomei, Tan Kun, et al. Dimensionality Reduction and Feature Extraction from Hyperspectral Remote Sensing Imagery Based on Manifold Learning[J]. Geomatics and Information Science of Wuhan University, 2011, 36(2): 148-152 (杜培军, 王小美, 谭琨, 等. 利用流形学习进行高光谱遥感影像的降维与特征提取[J]. 武汉大学学报·信息科学版, 2011, 36(2): 148-152) |
| [12] | De Witt D J, Naughton J F, Schneider D A, et al. Practical Skew Handling in Parallel Joins[C]. The 18th VLDB Conference, Vancouver, British Columbia, Canada, 1992 |
 2015, Vol. 40
2015, Vol. 40



