文章信息
- 许剑辉, 舒红
- XU Jianhui, SHU Hong
- 基于DEnKF方法的考虑次网格变异性的MODIS雪盖同化
- DEnKF-based Assimilation of MODIS-Derived Snow Cover Products into Common Land Model Considering the Model Sub-grid Heterogeneity
- 武汉大学学报·信息科学版, 2016, 41(2): 156-162
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 156-162
- http://dx.doi.org/10.13203/j.whugis20140039
-
文章历史
- 收稿日期: 2014-09-29

2. 广州地理研究所广东省地理空间信息技术与应用公共实验室, 广东广州, 510070
2. Guangdong Open Laboratory of Geospatial Information Technology and Application, Guangzhou Institute of Geography, Guangzhou 510070, China
积雪是气候系统非常重要的组成部分,直接制约着地表能量和水平衡[1]。刻画积雪特征的属性主要包括雪盖、雪密度、雪水当量和雪深,其中雪水当量和雪深常被用来监测和预测雪灾。目前,许多研究主要通过陆面模型模拟和遥感定量反演的方式估计雪水当量或雪深。然而,由于受到驱动数据、参数初始值等不确定性的影响,模型模拟的积雪数据具有很大的不确定性;而遥感定量反演的积雪具有偏差大[2, 3]、空间分辨率低等不足。数据同化是一种将物理机理模型和观测数据结合起来分析的优化方法,通过数据同化将陆面模型和遥感反演积雪数据有效结合起来,能够获取更高精度的积雪数据。
目前,国内外学者发展了一些积雪数据同化方法[4, 5, 6],并已应用到陆面模型中获取高精度的积雪产品。Rodell和Houser提出了一种基于规则的直接插入同化方法[7],该方法已成功地将MODIS雪盖数据同化到陆面模型中获取高精度的雪水当量[8]。结合AMSR-E反演的25 km空间分辨率的雪水当量产品,De Lannoy等发展了4种基于集合卡尔曼滤波的多尺度数据同化方案,将粗尺度(25 km)的雪水当量数据同化到细尺度(1 km)的陆面模型中[9, 10],获取高空间分辨率的雪水当量产品。根据不同的观测算子,Su等[1]和Arsenault等[11]利用EnKF(ensemble Kalman filter)将MODIS雪盖数据同化到CLM(community land model)陆面模型,获取高质量的雪水当量数据。基于规则的直接插入方法不需要考虑模型或观测的不确定性,但前提是假设观测数据是精确的。集合卡尔曼滤波的积雪数据同化方法需要对观测数据进行扰动,这样会对观测数据引入不确定性,如雪盖面积为0或者100%时,对雪盖数据进行扰动会出现负值或超过100%的情况。最近发展起来的一种同化方法——确定性集合卡尔曼滤波(deterministic ensemble Kalman filter,DEnKF),不需要对观测数据进行扰动,是传统EnKF的修正,能够较好地逼近理论卡尔曼滤波的分析误差协方差[12]。
通用陆面模型[13](common land model,CoLM)进行模拟时考虑了次网格的变异性,田向军等[14]在进行土壤湿度同化实验时,发现不考虑模型次网格变异性的直接同化会使同化结果出现偏差。基于此,本文发展了一种基于DEnKF同化方法和CoLM模型的考虑次网格变异性的MODIS雪盖同化方案,并利用2007年11月至2008年4月北疆阿勒泰地区5个气象站点的逐日雪深观测数据对同化结果进行了验证分析。
1 陆面模型及数据同化方法 1.1 通用陆面模型通用陆面模型是戴永久等[13]结合了BATS(biosphere-atmosphere transfer scheme)、LSM(land surface model)和IAP94(the 1994 version of the chinese academy of science institute of atmospheric physics LSM)三个模型的优点发展起来的新一代陆面过程模型,它充分考虑了生物物理化学过程、植被动力学、碳循环、辐射传输和水文等众多过程,对土壤-植被-大气之间的能量与水分的传输有较好的描述。它采用USGS植被分类方式,每个网格可再分为24种下垫面类型,把每个面积大于0的下垫面划分为相应的次网格(sub-grid),每一个次网格只表示一种植被覆盖类型,通过模型次网格的变异性来精细地反映出地表的非均匀性特征。垂直方向上,CoLM模型在土壤之上根据积雪厚度的变化划分了至多五层的雪层。首先通过雪层累加计算得到每一个次网格的雪深估计值,然后按照次网格面积权重加权平均得到整个网格的雪深。CoLM模型估计雪深的公式为:
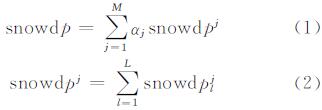
式中,snowdp为模型输出的网格雪深预测值;snowdpj为通过雪层累加得到的次网格雪深预测值;αj为次网格的面积权重;M为次网格数目;snowdplj为第j个次网格第l层雪层的雪深预测值;L为积雪层数。
1.2 DEnKF同化方法集合卡尔曼滤波算法(EnKF)是Evensen在1994年提出的顺序数据同化算法[15]。其基本思想是利用蒙特卡罗方法的思想估计模型状态变量和观测变量的误差协方差(方差-协方差),再利用误差协方差和观测资料在某种代价函数或优化准则下进行模型与观测状态的最优融合分析,最终获取更高精度的预测结果。EnKF数据同化的基本过程为[16]:
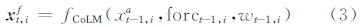
式中,fCoLM为模型预测算子;(xt-1,ia表示t-1时刻第i个集合成员的分析值;xt,if表示t时刻第i个集合成员的预测值;forct-1,i表示t-1时刻的大气强迫数据;wt-1,i表示对模型状态变量的扰动。
通过式(4)更新状态变量的集合成员:
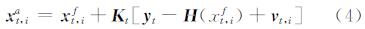
式中,xt,ia为t时刻模型状态变量的分析值;xt,if为t时刻模型状态变量的预测值;yt为观测数据;H为观测算子,将模型预测的状态向量映射到观测向量空间;vt,i为服从均值为0、方差为Rt的高斯噪声。卡尔曼增益Kt的计算公式为:
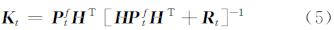
式中,Ptf表示模型预测误差的协方差矩阵;Rt为观测误差的协方差矩阵。
确定性集合卡尔曼滤波(DEnKF)同化方法[12]是由Sakov和Oke(2008)提出的,与EnKF方法类似,但不需要对观测数据加入扰动,可以减少观测扰动引入的不确定性,能更好地逼近Kalman滤波分析误差协方差的理论值。其基本过程是将集合成员分解成集合均值和集合扰动,分别对集合均值和集合扰动单独进行更新:
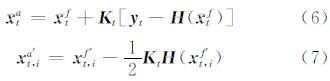
式中,Kt与传统EnKF的卡尔曼增益一致;Xta为更新后的模型状态变量的分析集合均值;Xtf为模型状态变量预测值的均值;xt,if′和xt,ia′分别为预测集合扰动和分析集合扰动。将更新的分析集合均值与分析集合扰动相加得到更新后的集合。与一般卡尔曼滤波不同的是,分析集合扰动的更新(式(7))不需要对观测数据进行扰动。
1.3 基于DEnKF方法的MODIS雪盖同化本实验将雪深作为CoLM模型的状态变量,根据式(3)得到雪深的预测值xt,if。由于CoLM按次网格形式计算雪深预测值,因此xt,if为:
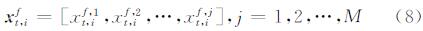
式中,xt,if,j为t时刻第j个次网格雪深的预测值;M为每个网格的次网格数目。雪盖消融曲线描述的是雪深与雪盖之间的关系,如式(9)所示:
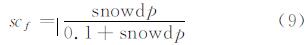
式中,snowdp为雪深(m);scf为积雪覆盖面积(%)。
在MODIS雪盖数据同化中,将式(9)作为同化的观测算子,结合式(5)至式(7)实现基于DEnKF的MODIS雪盖同化。由于式(6)中的yt为同化网格对应的MODIS雪盖,而利用观测算子得到的是基于次网格的雪盖,因此,模型模拟的网格雪盖为所有次网格的雪盖通过次网格面积权重累加得到:
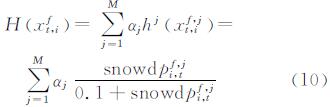
式中,αj为次网格的面积权重;M为次网格数目。
2 数据及实验方案设计 2.1 实验数据阿勒泰地区的地形复杂,气候多变,属于新疆北疆地区雪灾发生比较严重的地方。本文选取阿勒泰地区的5个雪深观测站点作为研究区域,观测站点的详细信息如表 1所示。实验分别选取5个站点2007年11月1日至2008年4月30日的日雪深观测数据作为同化结果的验证数据(站点雪深数据由中国气象局乌鲁木齐沙漠气象研究所提供)。
| 站名 | 经度/(°) | 纬度/(°) | 高程/m |
| 阿勒泰(Aletai) | 88.083 | 47.733 | 737 |
| 布尔津(Buerjin) | 86.867 | 47.4 | 456 |
| 富蕴(Fuyun) | 89.517 | 46.983 | 826 |
| 吉木乃(Jimunai) | 85.867 | 47.433 | 984 |
| 青河(Qinghe) | 90.383 | 46.667 | 1 200 |
CoLM模型所需的驱动数据为中国西部环境与生态科学数据中心提供的2007年1月1日至2008年4月30日空间分辨率为0.1°、时间分辨率为3 h的地面气象要素驱动数据集,包括入射短波辐射、入射长波辐射、降水、气温、气压、风速和绝对湿度。
雪盖数据是从美国国家冰雪数据中心(http://nsidc.org/data/)下载的由MODIS提供的MOD10C1雪盖产品。MOD10C1是逐日气候模型网格产品,空间分辨率为0.05°。
2.2 同化实验方案设计本文设计了模型模拟、open-loop和DEnKF三个对比实验。其中,open-loop只进行集合预测,不进行同化;DEnKF采用本文方法进行MODIS雪盖同化实验。open-loop和DEnKF实验都需要对大气强迫数据和模型状态进行扰动,以生成集合成员,集合大小通常设置为20。参考文献[9],分别对大气强迫数据入射短波辐射、入射长波辐射、降水和气温进行扰动;模型状态雪深变量采用均值为1、标准差为0.01的乘法扰动方式。
利用空间分辨率为0.1°的大气强迫数据驱动CoLM模型。CoLM模型的运行时间从2007年1月1日至2008年4月30日,系统预热(spin-up)的训练时间从2007年1月1日开始直到MODIS的雪盖出现,当MODIS雪盖出现时进行同化实验。由于CoLM模型驱动数据的空间分辨率为0.1°,为了保持遥感雪盖观测数据的空间分辨率与模型模拟的空间分辨率一致,对MOD10C1雪盖产品的4个相邻像元值进行平均,计算得到0.1°分辨率的雪盖数据。由于MODIS反演的雪盖数据受到云的影响,为了减少云盖对同化结果的影响,当云盖面积超过50%时,不进行同化。同时,参考文献[11],每个观测站点对应雪盖数据的标准误差均设为30%。
采用平均误差(mean error,ME)、平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)和决定系数R2(determination coefficient)来评价模型模拟、open-loop和雪盖同化的实验结果。
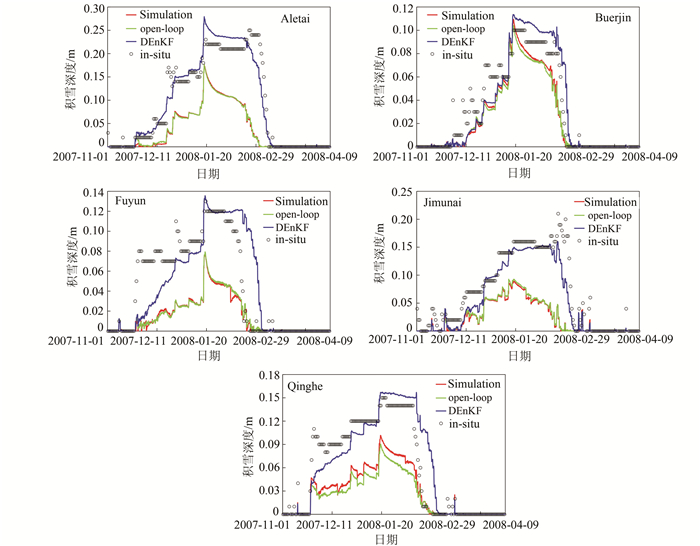
3 结果分析 3.1 基于MODIS雪盖数据的同化结果图 1为2007年11月至2008年4月阿勒泰地区5个气象观测站模拟、open-loop、同化和观测的雪深数据比较。由图 1可看到,CoLM雪深的模拟结果整体上被低估,远低于地面观测雪深,偏差较大;考虑次网格变异性的MODIS雪盖数据同化提高了CoLM模型对雪深过低的估计,使同化结果接近观测值,与地面站点雪深观测保持较好的一致性。
|
| 图 1 不同站点的雪深同化结果的比较 Fig. 1 Data Assimilation Comparisons of Snow Depths of Simulation,open-loop,DEnKF and in-situ at Different Stations |
对于阿勒泰观测站点,与地面雪深观测数据相比较,模型模拟的雪深数据整体上被低估,平均误差为6.7 cm,其均方根误差达到了9.04 cm,决定系数R2为0.652 1;open-loop的雪深数据与模型模拟的结果很接近,平均绝对误差较模型模拟的雪深仅减少了0.04 cm;而同化后雪深的精度有了很大的提高,平均绝对误差和均方根误差分别减少了4.83 cm和6.34 cm,精度分别提高了72.52%和70.13%,R2达到0.920 7(表 2)。同化后的雪深与地面观测雪深整体上保持很好的一致性,平均误差仅为0.03 cm,但是在2008年1月18日至2月23日雪深达到最大值期间,同化雪深被高估了(图 1)。吉木乃观测站具有与阿勒泰观测站类似的实验结果,与模型模拟结果相比,平均误差、平均绝对误差和均方根误差分别减少了68.16%、65.36%和60.56%,与地面观测雪深拟合的决定系数提高了0.398 4,达到0.868 7(表 2)。然而,同化后的雪深整体上被低估了(图 1),其偏差值为1.78 cm。
| 方法 | Simulation模拟 | open-loop集合预测 | DEnKF同化 | |||||||||
| ME/m | MAE/m | RMSE/m | R2 | ME/m | MAE/m | RMSE/m | R2 | ME/m | MAE/m | RMSE/m | R2 | |
| Aletai | -0.066 6 | 0.066 6 | 0.090 4 | 0.652 1 | -0.066 2 | 0.066 2 | 0.090 4 | 0.652 8 | 0.000 3 | 0.018 3 | 0.027 0 | 0.920 7 |
| Buerjin | -0.009 6 | 0.010 3 | 0.015 5 | 0.900 3 | -0.010 5 | 0.011 0 | 0.016 3 | 0.905 8 | 0.000 5 | 0.009 9 | 0.015 1 | 0.879 5 |
| Fuyun | -0.036 5 | 0.036 7 | 0.047 8 | 0.785 7 | -0.036 1 | 0.036 4 | 0.047 4 | 0.778 3 | -0.002 1 | 0.019 8 | 0.032 0 | 0.587 7 |
| Jimunai | -0.055 9 | 0.056 3 | 0.074 8 | 0.470 3 | -0.054 4 | 0.054 7 | 0.073 2 | 0.483 4 | -0.017 8 | 0.019 5 | 0.029 5 | 0.868 7 |
| Qinghe | -0.036 6 | 0.036 9 | 0.046 8 | 0.925 6 | -0.042 9 | 0.043 2 | 0.054 7 | 0.901 2 | 0.000 4 | 0.016 7 | 0.026 6 | 0.802 5 |
对于布尔津、富蕴和青河观测站点,open-loop估计的雪深与CoLM模拟的雪深比较接近,并没有都优于模拟结果,如青河观测站,open-loop实验计算的平均误差、平均绝对误差和均方根误差等都劣于模拟结果(表 2)。因为open-loop的实验结果是通过集合平均计算得到的,一般情况下,在集合数比较大时,其结果优于模拟结果。然而在实验中,本文依据统计样本量经验性准则采用20个集合成员进行实验,较少的集合数并没有较好地提高雪深的估计精度。另外,对大气强迫数据和模型状态雪深变量分别进行扰动而引入的不确定性会导致雪深的估计误差增大。同化结果较模型模拟和open-loop结果有比较明显的改善,但同化后的雪深与地面观测雪深的整体相关性反而减少了(表 2)。从图 1中的Buerjin、Fuyun和Qinghe可以看出,在2008年1月20日(模拟和站点观测雪深达到最大值)前,雪盖同化有效地提高了雪深估计精度,雪深估计值略低于地面雪深观测值(富蕴站地面雪深观测值比同化结果要高一些);在2008年1月20日之后,雪盖同化过高地优化CoLM模拟的雪深,使得雪深改善的幅度较大,与地面雪深观测值相比有些偏大(图 1中的Fuyun和Qinghe);布尔津观测站同化后的雪深略高于地面雪深观测值,如图 1中Buerjin所示。这是因为2008年1月20日之后雪盖同化实验设置的雪盖观测误差方差较小(实验中设置时间不变的雪盖数据误差标准差为30%),导致了雪盖同化对雪深过高的估计。根据式(6),同化结果与背景误差协方差矩阵和观测误差协方差矩阵密切相关。观测误差协方差矩阵越大,观测值提供的信息就越少,同化结果向模型预测值靠近。因此,相对较小的雪盖观测误差方差给同化结果增加了更多的观测积雪信息。
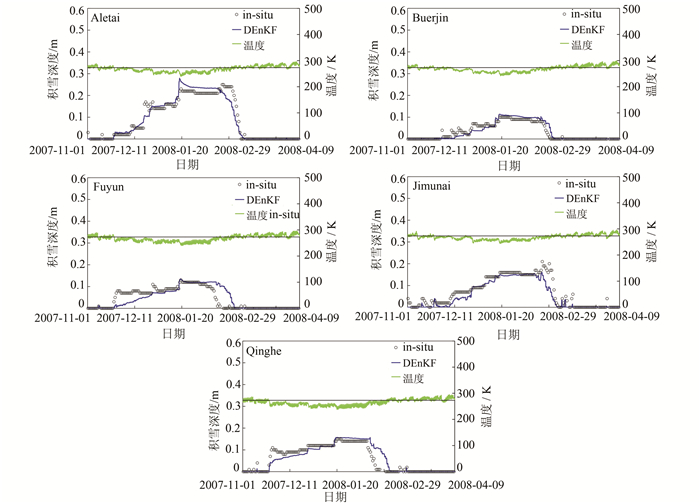
3.2 雪深时间序列分析图 2显示了不同地面观测站点雪深、同化后的雪深与气温在积雪期、融雪期的时间变化趋势。从图 2可以看出,雪盖同化估计的雪深与地面观测雪深具有基本一致的时间变化趋势,同化结果很好地反映了积雪的时间变化趋势。雪深与气温具有很强的负相关性,在雪期内,气温越低,积雪深度越深。在2008年1月20日左右,雪深达到最大值,气温降低到最低温度;2007年11月1日至2008年1月20日为积雪累积期,雪深平缓增加;2008年1月20日至2月23日为积雪平稳期,即雪深达到最大值后,大概一个月时间内积雪深度保持较稳定的状态,变化幅度不大;2008年2月23日至3月20日为融雪期,积雪变化非常大,雪深减少的速率比较快。从图 2也可以看出,积雪累积期比较长,大概有50天左右,积雪平稳期大概30天左右,融雪期比较短,大概25天左右。对于富蕴观测站点和青河观测站点,由于雪盖同化过优化模拟雪深数据,导致融雪期往后推延了7天左右。
|
| 图 2 不同地面观测站点雪深、同化后的雪深与气温的时间序列图(黑色直线表示冰点,为273.15 K) Fig. 2 Time Series for Snow Depth from in-situ and DEnKF-based Assimilation,and Air Temperature from WestDC Dataset |
基于确定性集合卡尔曼滤波同化算法(DEnKF)和CoLM模型,本文发展了一个考虑次网格变异性的积雪数据同化方案,利用MODIS雪盖数据进行了同化实验,应用阿勒泰地区5个气象站点的雪深观测数据进行了结果验证。
1) 基于DEnKF雪盖同化方案能明显地提高雪深的估计精度,较好地反映出积雪深度在累积期、平稳期和融雪期的变化特性。
2) 确定性集合卡尔曼滤波同化方法能减少因对观测数据进行扰动而引入的误差。对于MODIS雪盖同化来说,积雪覆盖面积取值在0~100%之间,如在积雪平稳期,雪盖面积一般都达到100%,如果对雪盖面积进行扰动,会产生异常值,出现雪盖面积大于100%的情况,这是不合理的。
3) 整体上,阿勒泰站点雪深最大,特别在积雪平稳期,雪深都超过了20 cm;其他站点的雪深最大值也有13 cm以上。
基于确定性集合卡尔曼滤波的雪盖同化方案受到CoLM模型误差、MODIS雪盖观测误差、集合大小、雪盖观测算子等因素的影响。在本实验中,由于只采用了比较简单的雪盖观测算子和时间不变的观测误差方差,同化结果存在比较明显的推延现象,如富蕴观测站和青河观测站雪盖同化后,积雪融雪期往后推延了7天左右。这是由于实验中使用了不准确的观测精度引起的。在今后工作中,需要准确地估计MODIS雪盖产品的误差,考虑随积雪季节变化的雪盖误差方差和合理的雪盖观测算子。此外,由于MODIS雪盖受到云的影响,本文只在云量少于50%的情况下进行雪盖同化实验,如何减少云的影响,以让更多的雪盖数据参与同化实验,也是将来需要进一步研究的内容。
致谢:感谢中国气象局乌鲁木齐沙漠气象研究所提供的站点雪深数据和寒区旱区科学数据中心(http://westdc.westgis.ac.cn)提供的高时空分辨率地面气象要素驱动数据集。
| [1] | Su H, Yang Z,Niu G, et al. Enhancing the Estimation of Continental-scale Snow Water Equivalent by Assimilating MODIS Snow Cover with the Ensemble Kalman Filter[J]. Journal of Geophysical Research:Atmospheres (1984-2012), 2008, 113(D8):D08120 |
| [2] | Liu Hai, Chen Xiaoling, Song Zhen, et al. Study of Characteristic Parametric Selection and Model Construction for Snow Depth Retrieval from MODIS Image[J]. Geomatics and Information Science of Wuhan University, 2011, 36(1):113-116(刘海,陈晓玲,宋珍,等. MODIS影像雪深遥感反演特征参数选择与模型研究[J]. 武汉大学学报·信息科学版, 2011, 36(1):113-116) |
| [3] | Liu Yan,Ruan Huihua, Zhang Pu, et al. Kriging Interpolation of Snow Depth at the North of Tianshan Mountains Assisted by MODIS Data[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4):403-405(刘艳,阮惠华,张璞,等. 利用MODIS数据研究天山北麓Kriging雪深插值[J]. 武汉大学学报·信息科学版, 2012, 37(4):403-405) |
| [4] | Liu Y, Peters-Lidard C D, Kumar S, et al. Assimilating Satellite-Based Snow Depth and Snow Cover Products for Improving Snow Predictions in Alaska[J]. Advances in Water Resources, 2013, 54:208-227 |
| [5] | Zaitchik B F, Rodell M. Forward-looking Assimilation of MODIS-derived Snow-covered Area into a Land Surface Model[J]. Journal of Hydrometeorology, 2009, 10(1):130-148 |
| [6] | Slater A G, Clark M P. Snow Data Assimilation via an Ensemble Kalman Filter[J].Journal of Hydrometeorology, 2006, 7(3):478-493 |
| [7] | Rodell M, Houser P R. Updating a Land Surface Model with MODIS-derived Snow Cover[J]. Journal of Hydrometeorology, 2004, 5(6):1064-1075 |
| [8] | Fletcher S J, Liston G E,Hiemstra C A, et al. Assimilating MODIS and AMSR-E Snow Observations in a Snow Evolution Model[J]. Journal of Hydrometeorology, 2012, 13(5):1475-1492 |
| [9] | De Lannoy G E L J, Reichle R H, Houser P R, et al. Satellite-scale Snow Water Equivalent Assimilation into a High-resolution Land Surface Model[J]. Journal of Hydrometeorology, 2010, 11(2):352-369 |
| [10] | De Lannoy G E L J, Reichle R H, Arsenault K R, et al. Multiscale Assimilation of Advanced Microwave Scanning Radiometer-EOS Snow Water Equivalent and Moderate Resolution Imaging Spectroradiometer Snow Cover Fraction Observations in Northern Colorado[J]. Water Resources Research, 2012, 48(1):W01522 |
| [11] | Arsenault K R, Houser P R, De Lannoy G E L J, et al. Impacts of Snow Cover Fraction Data Assimilation on Modeled Energy and Moisture Budgets[J]. Journal of Geophysical Research:Atmospheres, 2013, 118(14):7489-7504 |
| [12] | Sakov P, Oke P R. A Deterministic Formulation of the Ensemble Kalman Filter:An Alternative to Ensemble Square Root Filters[J]. Tellus A, 2008, 60(2):361-371 |
| [13] | Dai Y, Zeng X, Dickinson R E, et al. The Common Land Model[J].Bulletin of the American Meteorological Society, 2003, 84(8):1013-1023 |
| [14] | Tian Xiangjun,Xie Zhenghui. A Land Surface Soil Moisture Data Assimilation in Consideration of the Model Subgrid-scale Heterogeneity and Soil Water Thawing and Freezing[J]. Science in China (D):Earth Science, 2008, 38(6):741-749(田向军,谢正辉. 考虑次网格变异性和土壤冻融过程的土壤湿度同化方案[J]. 中国科学D辑:地球科学. 2008, 38(6):741-749) |
| [15] | Evensen G. Sequential Data Assimilation with a Nonlinear Quasi-geostrophic Model Using Monte Carlo Methods to Forecast Error Statistics[J]. Journal of Geophysical Research:Oceans (1978-2012), 1994, 99(C5):10143-10162 |
| [16] | Evensen G. The Ensemble Kalman Filter:Theoretical Formulation and Practical Implementation[J]. Ocean Dynamics, 2003, 53(4):343-367 |
 2016, Vol. 41
2016, Vol. 41



