文章信息
- 胡勇, 罗文, 俞肇元, 冯琳耀
- HU Yong, LUO Wen, YU Zhaoyuan, FENG Linyao
- 多维时空场数据的多模式张量表达模型
- Multi-mode Tensor Expression Model of Multidimensional Spatio-temporal Field Data
- 武汉大学学报·信息科学版, 2015, 40(7): 977-982
- Geomatics and Information Science of Wuhan University, 2015, 40(7): 977-982
- http://dx.doi.org/10.13203/j.whugis20130491
-
文章历史
- 收稿日期:2013-09-17
2. 南京师范大学虚拟地理环境教育部重点实验室, 江苏 南京, 210023
2. Key Laboratory of Virtual Geographical Environment, Ministry of Education, Nanjing Normal University, Nanjing 210023, China
对地观测技术、物联网技术以及全球变化模拟等的快速发展,积累了海量的多维时空场数据,其数据量级及复杂度均呈指数增加的态势[1],并伴随着数据复杂性与多样性的增强[2, 3, 4]。以NetCDF、HDF等文件格式组织的时空场数据管理系统主要基于N维数组模型,一定程度上难以实现数据的高效压缩、存储与快速传输[5, 6]。从数据库和文件格式集成角度构建的诸如SciDB、Rasdaman等数据库管理系统在复杂对象和连续对象的表达和建模,尤其是在时空过程分析以及时空模拟的支撑上,仍存在明显的不足[7, 8]。例如GrADS[9]及Vis5D[10]的场数据分析与可视化系统多是基于二维分析扩展而来,对数据多维度特征分析仍显不足。诸如Hadoop等并行计算平台主要通过MapReduce技术,实现数据的高度并行化以加速数据计算[11],然而,如何实现Hadoop平台与传统的编程模式的有效集成是基于上述策略的海量数据管理可用性的关键[12]。
张量是矩阵的高维扩展,具有明确数学含义并可直接支撑数学计算的高维数组结构,对多维表达的内蕴支持可以为时空场数据表达提供原生的数学支撑[13]。发展的张量代数、张量分解以及高性能软件包可以实现基于张量数据结构的复杂分析与计算,并能对现有时空分析方法进行集成[14]。以主张量分解为代表的张量表达、逼近与分析方法的迅猛发展,提供了多维时空数据的低阶逼近方法,并表现出更好的结构保形性,有助于揭示多维时空数据不同维度间的耦合作用关系[13]。以张量分析为基础发展的高维数据特征解析方法(如PARAFAC、Tucker-N、HOSVD等)也在多个领域得到运用[15]。本文引入具有多维统一与坐标无关特性的张量数学结构,研究基于张量的多维时空场数据表达模型,设计不同模式的张量表达结构,进而构建多模式张量时空场数据分析,并利用卫星测高数据对相关存储与分析性能进行了测试与验证。
1 基于张量的时空场数据组织时空场数据通常具有多维度、海量性等特征,借鉴张量的存储方式,对时空场进行编组,利用张量的多维度运算特征构建多层次的分解结构和基于维度树的组合结构。
1.1 时空场数据的张量编组一个 N阶张量可记为 A ∈RL1×L2×…×LM,其中Li表示第i阶的维度大小。对于给定的张量 A ∈RL1×L2×…×LM,可根据选定的维度对其进行透视、拆分和分割。选取任意方向ei和点Ti,可将[Ti(e1)Ti(e2)Ti(e3)]展开成如下形式:
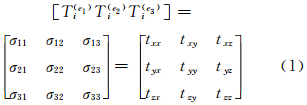
利用上述结构可实现海量时空场数据的张量编组,对于给定维度(L1×L2×…×Ln)的地学数据,首先定义张量空间 A ∈RL1×L2×…×Ln,则地学场数据{Ft1,Ft2,…,Ftn}可表达为如下形式:
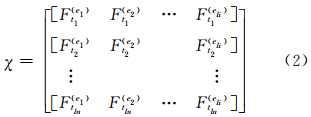
其中每个 [Ft1(e1),Ft1(e1),…,Ft1(eli) 都被称为一个块 (block),根据实际需要,可将每个块重新排列成矩阵的形式,由不同的维度重排可得到不同的矩阵化结果。
1.2 时空场数据的层次分解结构张量的多维度特征及其丰富的多维算子,使得可以对多维时空场的时间、空间和属性结构进行组合、拆分,得到形如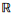 T×
T×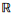 S×
S×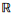 A1×A2×…×Ad的层次结构。根据其分解模式的差异,产生了两种层次张量的分解方法,分别为逐层分解的 PARAFAC模型[16]和包含一个核结构的Turker模型[12]。PARAFAC模型的分解方式与主成分类似,依次分解出原始张量中的主子张量结构;Turker模型则充分利用了张量结构的维度混合特征与维度运算,其一阶张量分解公式为:
A1×A2×…×Ad的层次结构。根据其分解模式的差异,产生了两种层次张量的分解方法,分别为逐层分解的 PARAFAC模型[16]和包含一个核结构的Turker模型[12]。PARAFAC模型的分解方式与主成分类似,依次分解出原始张量中的主子张量结构;Turker模型则充分利用了张量结构的维度混合特征与维度运算,其一阶张量分解公式为:
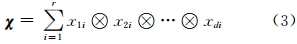
式中,χ 为原始张量;r为分解阶数;x1i,x2i,…,xdi分别是第i个维度上的系数;“ ”为张量外积,可实现层次张量的重构。相对于传统的主成分分析,一阶张量分解可以实现对张量任意维度参数特征的分析与描述,并可根据不同维度的组合对其进行结构与过程重构,具有更好的整体性,可用于数据压缩。然而如何构建稳健、唯一和高效的张量分解模型仍有待进一步研究。
”为张量外积,可实现层次张量的重构。相对于传统的主成分分析,一阶张量分解可以实现对张量任意维度参数特征的分析与描述,并可根据不同维度的组合对其进行结构与过程重构,具有更好的整体性,可用于数据压缩。然而如何构建稳健、唯一和高效的张量分解模型仍有待进一步研究。
层次张量树构建,基于上述一阶张量分解的Turker模型可构建基于迭代Tucker结构的层次张量分解方法,进而基于张量的维度层级结构进行张量的子空间分解,形成基于树状结构的张量层次表达。其层次SVD分解可以定义为:
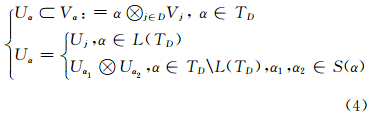
其中TD为维度树,满足:①树TD所有叶子非空;②D是树TD的根节点;③TD中任意对象α∈TD 在grade(α)>2 时均具有两个子节点α1,α2∈TD。给定张量v,及维度树TD,则有v∈V=a j∈DVj,并可用基于维度树TD的一系列层次子空间Uα加以表达。对上述层次张量分解,可以根据相应的系数逐层重构出原始数据,其重构规则如下:
j∈DVj,并可用基于维度树TD的一系列层次子空间Uα加以表达。对上述层次张量分解,可以根据相应的系数逐层重构出原始数据,其重构规则如下:
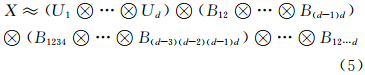
上述模型利用张量的层次分解实现了数据规模的压缩,为基于张量的数据存储与检索提供基础。
2 时空场数据多模式分析框架受地学时空场数据本身的复杂性和分析需求的多样性制约,传统时空场数据分析系统多采用不同的数据类型组织,各分析模型之间的差异性较大。基于张量数据组织的多维统一特征与直接面向维度的张量运算对构建统一高效的数据流表达和结构一致的业务流分析模板具有重要意义。
2.1 张量多模式表达特征分析不同模式的张量数据结构及其特征如表 1所示。原始多维数组的张量表达具有较高的数据冗余,更接近于数据原始采集的状态,适用于海量时空场数据的采集与结果输出;传统的张量分解可以实现不同维度的特征提取、关系识别与过程重建,适用于数据分析;层次张量结构则为张量数据的压缩和检索提供了原生的支持,更适用于海量时空场数据的存储于传输。对上述3种张量结构的综合运用,将可有效支撑从原始数据采集、数据分析与数据存储的时空场分析流程。
| 张量 | 数据结构与存储 | 主要业务流阶段 |
| 立方体结构 | 按照特定的维度矩阵化后存储,精度最高但数据冗余大 | 精度高,可视化方便,用于海量时空场数据的采集与结果输出 |
| 维度分解 结构 | 存储按维度分解的子张量系数,一定程度压缩数据大小,随精度要求提高,压缩效果降低 | 各维度系数反映了其所在维度的特征,一般用于关系识别与过程重建 |
| 维度树 结构 | 树状结构存储,各节点为不同维度层次下的数据矩阵,维度分层结构利于数据的动态更新与传输 | 为张量数据的压缩和检索提供了支持,可用于海量时空场数据的存储与传输 |

|
| 图 1 张量层次分解与维度树构建 Fig. 1 Tensor Decomposition and Tensor Tree Construction |
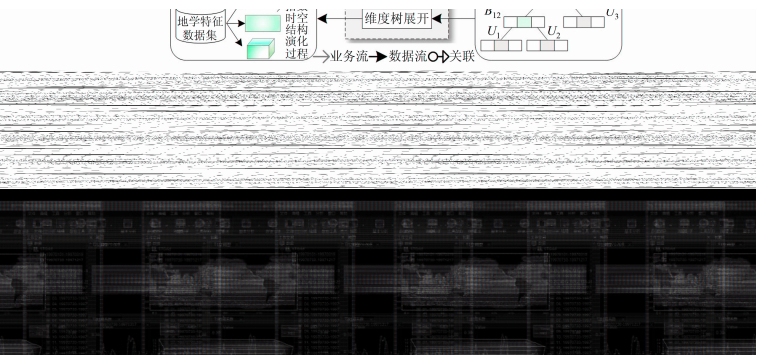
为兼顾数据存储与时空分析的需求,面向不同业务需求设计不同的数据表达形式,并形成相应的数据流结构(图 2)。张量是整个数据组织与建模的核心,为兼顾数据采集、分析和存储的全过程,分别设计面向多维数据的张量表达结构、面向地学特征分析的系数张量结构和面向压缩存储与共享的层次张量结构。三者统一于张量表达与分析框架并可通过张量运算相互转换,进而可设计海量时空场数据分析的业务流程:① 海量数据组织与变换;② 张量数据操作与检索;③ 基于主张量的数据特征分析;④基于主张量时空重构演化分析;⑤ 结果可视化与表达;⑥ 数据存储与共享。
|
| 图 2 时空场数据分析数据流结构 Fig. 2 Data Flow of Spatio-temporal Field Data Analysis |
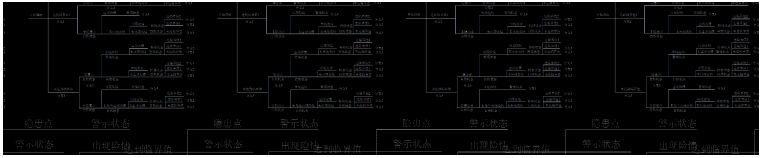
张量结构的灵活性与可计算性使其可支撑从数据采集到数据分析的全过程,且可以根据数据处理的流程选取适当的数据结构进行分析模版构建。一个典型的分析模版如图 3所示,对于任意给定的地理时空场数据集,基于原始的张量结构进行张量数据建模,并根据数据分析的时空需求选取典型的样区和分析时段。对所选择的张量数据进行PARAFAC或Tucker N模式的张量分解,获得相应的分解系数。引入参照数据对张量分解获得的系数进行序列比对与特征滤波,进而获得原始时空场特征数据。利用张量积重建张量子空间,实现对给定维度组合特征及时空演化过程的重构与模拟。最后对结果进行特征驱动的可视化,以及基于维度树的数据入库与存储。

|
| 图 3 时空场特征分析模板 Fig. 3 Template of Spatio-temporal Field Data Analysis |
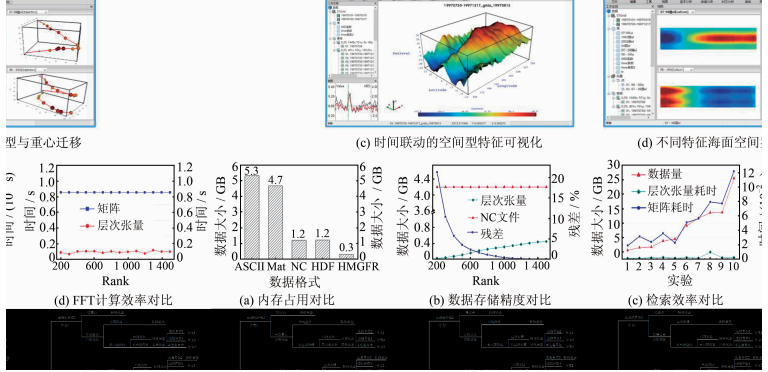
基于Visual C++ 2010进行算法开发,并进行性能测试。其测试环境如下:CPU:Intel Xeon E5645 (2.4 G),内存:16GB DDR-3,硬盘:7 200转1TB硬盘。操作系统平台为64位Windows 7。对全球1/4°格网化延迟平均海面异常卫星测高数据进行案例分析与性能评估。该数据由欧空 局下属的AVISO提供,时间分辨率为7 d间隔,共1 009个时间点。为验证张量结构的数据分析能力,选取赤道太平洋区域(15°S~15°N,150°E~100°W)和MEI指数(Multivariate ENSO Index)作为对比数据。对时空数据组织、基于主张量分解的时空特征解析、特征驱动的时空可视化以及时空演化轨迹分析等功能进行了系统演示,如图 4所示。并在此基础上,根据数据规模的不同,分别计算了传统方法与张量方法的存储空间占用、检索效率以及分析效率(图 5)。
|
| 图 4 海面时空场数据分析结果 Fig. 4 Results of Spatio-temporal Field of Sea Level Data |
|
| 图 5 算法性能评估 Fig. 5 Performance Evaluation of Algorithms |
结果显示,张量结构的储复杂度明显优于ASCII、Matlab Mat等通用格式和NetCDF、HDF等领域应用格式,可以有效降低磁盘与内存占用。相对于NetCDF文件(NC),基于层次张量的数据存储可以根据Rank的不同,实现表达精度与数据大小的有效平衡,并可在限定的内存容量下获得较少的数据精度损失。在检索和分析方面,基于张量的数据检索随数据规模增长时间复杂度变化不大,且其总耗时远小于基于矩阵的检索方式。对卫星测高数据FFT分析的效率对比可知,基于张量的数据分析效率优于传统的基于Matlab矩 阵形式的分析方式,因而为海量时空数据的管理与分析提供了良好的平台。
4 结 语本文利用张量组织时空场数据,设计了多模式的时空场数据构造与分析框架,提出了基于张量的多维时空场表达模型。通过对张量结构的讨论,设计时空场数据分析流程模版,实现了对海量时空场数据在数据采集-数据分析-数据存储的流程支撑。以张量为基础的时空场数据表达与分析方法可以有效地实现海量时空场数据的压缩存储,提升数据分析与计算效率。从而为海量时空场数据的表达与分析提供良好的理论与平台支撑。鉴于张量结构对复杂数学运算具有很好的支撑,发展基于张量的时空场数据分析与模拟方法是本文后续的研究方向。
致谢:感谢法国AVISO提供卫星测高数据;感谢EPFL高性能计算中心Daniel Kressner和Christine Tobler在张量方面的相关讨论。
| [1] | Guan X, Wu H. Leveraging the Power of Multi-Core Platforms for Large-Scale Geospatial Data Processing:Exemplified by Generating DEM from Massive LiDAR Point Clouds[J]. Computers & Geosciences, 2010, 36(10):1 276-1 282 |
| [2] | Miller H J, Han J. Geographic Data Mining and Knowledge Discovery[M]. Boca Raton,FL:CRC Press, 2009 |
| [3] | Li Qingquan,Li Deren. Big Data GIS[J]. Geomatics and Information Science of Wuhan University, 2014, 39(6):641-644(李清泉,李德仁. 大数据GIS[J]. 武汉大学学报·信息科学版, 2014, 39(6):641-644) |
| [4] | Zhang Xiaoxiang. Spatial Analysis in the Era of Big Data[J]. Geomatics and Information Science of Wuhan University, 2014, 39(6):655-659 (张晓祥. 大数据时代的空间分析[J]. 武汉大学学报·信息科学版, 2014, 39(6):655-659) |
| [5] | Rew R, Davis G. NetCDF:An Interface for Scientific Data Access[J]. Computer Graphics and Applications, IEEE, 1990, 10(4):76-82 |
| [6] | Duane W, Livingstone D, Kidd D. Integrating Environmental Models with GIS:An Object-oriented Approach Utilising a Hierarchical Data Format (HDF) Data Repository[J]. Transactions in GIS, 2000, 4(3):263-280 |
| [7] | Brown P G. Overview of SciDB:Large Scale Array Storage, Processing and Analysis[C].Proceedings of the 2010 ACM SIGMOD International Conference on Management of data, ACM, Indianapolis, Indiana, 2010 |
| [8] | Baumann P, Dehmel A, Furtado P, et al.The Multidimensional Database System Rasdaman[J]. ACM SIGMOD Record,1998,27(2):575-577 |
| [9] | Berman F, Chien A, Cooper K, et al. The GrADSProject:Software Support for High-Level Grid Application Development[J]. International Journal of High Performance Computing Applications, 2001, 15(4):327-344 |
| [10] | Hibbard B. Confessions of a Visualization Skeptic[J]. ACM SIGGRAPH Computer Graphics, 2000, 34(3):11-13 |
| [11] | White T. Hadoop:the Definitive Guide Inc Sebastopol[M]. CA:O'Reilly Media, 2012 |
| [12] | Liu Xiaojun, Xu Zhengquan, Pang Shaoming. A Massive Small File Storage Solution Combination of RDBMS and Hadoop[J]. Geomatics and Information Science of Wuhan University, 2013, 38(1):113-115 (刘小俊,徐正全,潘少明.一种结合RDBMS和Hadoop的海量小文件存储方法[J]. 武汉大学学报·信息科学版,2013,38(1):113-115) |
| [13] | Yu Zhaoyuan, Yuan Linwang, Luo Wen, et al. Tensor-based Topographical Spatial-temporal Field Data Organization and Analysis[J]. Remote Sensing Technology and Application, 2012, 27(5):699-705 (俞肇元, 袁林旺, 罗文, 等. 基于张量的地学时空场数据组织与分析方法[J]. 遥感技术与应用, 2012, 27(5):699-705) |
| [14] | Kolda T G, Bader B W. Tensor Decompositions and Applications[J]. SIAM Review, 2009, 51(3):455-500 |
| [15] | van Loan C. Future Directions in Tensor-Based Computation and Modeling[R].Unpublished NSF Workshop Report.5, Ottawa, Ontario, 2009 |
| [16] | Harshman R A, Lundy M E. Uniqueness Proof for a Family of Models Sharing Features of Tucker's Three-mode Factor Analysis and PARAFAC/CANDECOMP[J]. Psychometrika, 1996,61:133-154 |
 2015, Vol. 40
2015, Vol. 40



