文章信息
- 何俊, 刘万科, 张小红
- HE Jun, LIU Wanke, ZHANG XiaoHong
- 北斗短基线三频实测数据单历元模糊度固定
- Single Epoch Ambiguity Resolution of BDS Triple Frequency Measured Data Under Short Baseline
- 武汉大学学报·信息科学版, 2015, 40(3): 361-365
- Geomatics and Information Science of Wuhan University, 2015, 40(3): 361-365
- http://dx.doi.org/10.13203/j.whugis20130279
-
文章历史
- 收稿日期:2013-06-29
不管是传统的TCAR还是CIR方法,均是先固定超宽巷(EWL),再固定宽巷(WL),最后固定窄巷(NL)或原始模糊度[1, 2, 3],但由于是简单的取整,因此,其可靠性并不高。Teunissen将TCAR、CIR与LAMBDA进行了比较,指出前者仅适用于无几何(geometry-free,GF)模式,而后者则不受此限制,并且前者在模糊度解算的成功率上不会优于后者[4],但在计算速度上,后者则略显不足。近年来,三频模糊度解算的概念被逐步扩展,并发展成为几何(geometry-based,GB)模式[5, 6]。然而,现有理论都偏向解决静态中长基线的模糊度固定问题,采用的思路也都类似“EWL-WL-NL”的层叠式方法,针对NL模糊度难以固定的问题,采用多历元平滑予以固定,这并不适用于短基线模糊度的快速确定。而在传统动态定位中,由于频率有限,很难单历元准确固定载波模糊度,往往需要利用多个历元的观测值,这样就不得不面对周跳探测等复杂的数据预处理。另外,由于实测数据的缺乏,目前三频模糊度固定的理论都是采用模拟数据进行验证[5, 7, 8],其在实测数据上的效果如何则不得而知。
2012年底,北斗区域导航系统的建成为北斗三频模糊度的解算研究提供了实测数据。本文针对测姿、飞机编队等动对动短基线的实际应用场景,从理论上分析了影响其模糊度固定的主要因素,采用“EWL-EWL-EWL”的模糊度固定策略,对实测的北斗三频观测数据采用无几何模式与几何模式相结合的方法进行单历元模糊度固定。该方法避开了传统周跳探测等复杂的数据预处理过程,同时适用于静态和动态定位模式,为动对动相对定位场合的数据处理提供了新的解决思路。
1 GF模式与GB模式下的模糊度固定
北斗三频组合载波和伪距双差观测方程可表示为[6]:
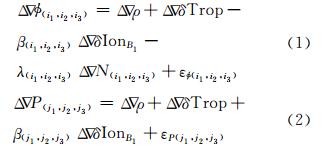
式中,φ(i1,i2,i3)和P(j1,j2,j3)分别表示组合系数为(i1,i2,i3)和(j1,j2,j3)的载波和伪距观测值;ρ为卫地几何距离;δTrop为对流层延迟量;β(i1,i2,i3)和β(j1,j2,j3)分别为组合载波和伪距上受到的一阶电离层放大因子( ionosphere scale factor,ISF),δIonB1为B1上受到的一阶电离层延迟量;λ(i1,i2,i3)和N(i1,i2,i3)分别为组合载波波长和模糊度;εφ(i1,i2,i3)和εP(j1,j2,j3)为组合载波和伪距的非模型化误差;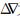 为双差算子。
为双差算子。
1.1 GF模式下的模糊度固定
用式(2)减去式(1),并顾及模糊度的整数特性,取整可得组合模糊度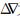 N:
N:
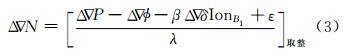
这就是无几何模式下的模糊度固定方法。当组合载波波长较长且其他误差(电离层、对流层、噪声等)得到了较好的消除时,直接利用上式即可算出组合模糊度。
1.2 GB模式下的模糊度固定
将式(1)和式(2)线性化,并写成矩阵形式为:
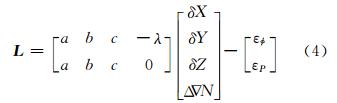
式中,L 为观测方程余数项。设历元t在基站A和流动站B共观测m颗卫星,则共可列出m-1 个形如式(4)的方程式组,迭代求解该方程式组,将得到的浮点模糊度及其对应的协因数阵输入LAMBDA进行模糊度固定,这就是几何模式下的模糊度固定方法。当观测值受传播误差或者噪声的影响较大,采用无几何模式固定可靠性不高时,即可采用几何模式下的模糊度固定方法进行搜索。
从式(3)和式(4)可以看出,不管是无几何模式还是几何模式下的模糊度固定方法,都受到电离层、对流层、观测噪声等因素的影响。为了消除或削弱这些影响,可以通过不同频率间的线性组合,构造具有长波长、弱(消)电离层、低噪声等特性的等效观测值,以提高模糊度固定的成功率。
2 北斗最佳组合观测值的选取
按照文献[6]给出的最优组合选取准则,以[-20,20]作为组合系数的搜索范围,并按文献[6, 9]给出的各类误差在整数域内进行搜索,可得短基线情况下前5个TNL最小的EWL组合如下(此处在GF模式下使用B1伪距固定组合模糊度,下同)。
从表 1中可以看出,超宽巷组合(0,-1,1) 波长为4.884 m,组合载波所受总误差对波长的影响只有0.034 7周左右。若在无几何模式下使用双频P码伪距组合(0,1,1)对其进行模糊度固定时,即为B2、B3组成的超宽巷M-W组合。此时,其总观测误差对组合波长的影响在正常情况下不会超过0.176 2周,可直接单历元取整固定。
| 组合系数 | 波长/m | GF下TNL/周 | GB下TNL/周 |
| (0,-1,1) | 4.884 | 0.247 5 | 0.034 7 |
| (1,4,-5) | 6.371 | 0.232 4 | 0.135 8 |
| (-1,-5,6) | 20.93 | 0.174 9 | 0.166 1 |
| (-1,-6,7) | 3.960 | 0.360 1 | 0.197 9 |
| (2,9,-11) | 9.158 | 0.328 5 | 0.301 4 |
第二组模糊度也可以从表 1中选取。当使用无几何模式在短基线情况下采用B1频点伪距对剩余组合进行模糊度固定时,总误差对组合波长的影响分别约为0.232 4周、0.174 9周、0.360 1周和0.328 5周。因此,本文选择组合(-1,-5,6)作为第二组待固定组合,使用无几何模式或者几何模式对其进行模糊度固定。
在前两组EWL模糊度固定之后,任何系数之和为0的组合模糊度均可直接由这两组模糊度计算得到。根据文献[10]所述,可将搜索范围锁定在系数之和为1的组合中。
从表 2第5列可知,所列组合的TNL均超过0.5周,很难在无几何模式下正确固定其模糊度,因此考虑采用几何模式进行固定。表中最右边一列给出了对30 m左右基线采用几何模式进行单历元模糊度固定的成功率。可以看出,使用几何模式对这5组组合进行单历元模糊度固定,其成功率都非常高。除去(-5,-4,10),另外4组组合的单历元成功率均接近100%,本文选取(-4,0,5)作为第三组最优组合。
| 组合系数 | 波长/m | GF下TNL/周 | GB下TNL/周 | GB下成功率/% |
| (-4,0,5) | 3.053 | 0.713 7 | 0.609 1 | 99.94 |
| (-4,1,4) | 8.140 | 0.616 5 | 0.623 7 | 99.92 |
| (-3,5,-1) | 3.574 | 0.696 1 | 0.629 0 | 99.93 |
| (-5,-4,10) | 5.861 | 0.654 4 | 0.639 7 | 88.21 |
| (-3,6,-2) | 13.32 | 0.627 0 | 0.651 1 | 99.91 |
3 三频模糊度解算步骤
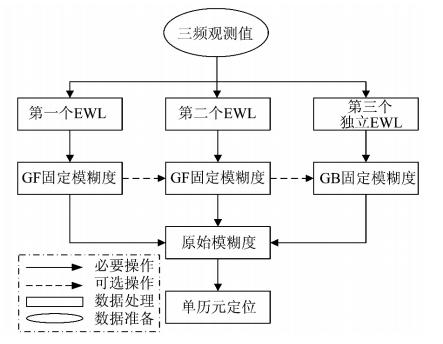
综上所述,无几何与几何模式相结合的三频模糊度固定步骤为(图 1):
|
| 图 1 三频模糊度固定步骤 Fig. 1 Step for Triple Frequency Ambiguity Resolution |
1) 使用伪距组合(0,1,1)在GF模式下计算(0,-1,1)的模糊度;
2) 使用伪距组合(1,0,0)在GF模式下计算(-1,-5,6)的模糊度;
3) 使用伪距组合(1,0,0)在GB模式下确定(-4,0,5)的模糊度。最后,还原原始载波模糊度。
4 实验与结果分析 4.1 静态短基线实验
本文采用的第一组数据为2012-12-29采用Trimble NetR9多频多系统接收机在武汉大学GNSS中心楼顶采集的静态短基线数据。两站基线长30多米,同步观测4 h,采样间隔设成1.0 s,观测弧段中仅GEO和IGSO卫星可见。
第一个超宽巷模糊度采用无几何模式固定。选取其中三组双差卫星对2-9,7-9和3-9(其中9为参考星)的模糊度实数值,并将使用TGO软件反算的模糊度作为真值,绘制两者之间的偏差,如图 2所示。可以发现采用GF模式解算出的N(0,-1,1)实数值与其真实值之间的差异基本都在±0.15周以内,可直接单历元取整固定。

|
| 图 2 第一组EWL组合浮点模糊度 Fig. 2 Float Ambiguity of the First EWL |
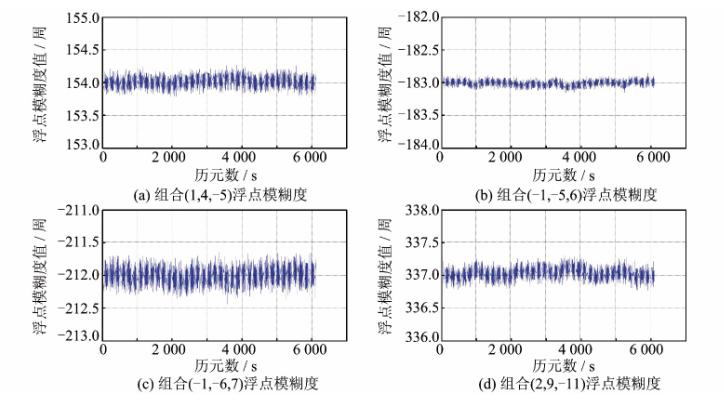
图 3给出了在无几何模式下使用B1频点的伪距求解双差卫星对7-9(其中9为参考星)的浮点组合模糊度N(1,4,-5)、N(-1,-5,6)、N(-1,-6,7)和N(2,9,-11)随时间的变化图。从图中可以看出,使用B1频点伪距在无几何模式下计算得到的N(-1,-5,6)的浮点值与最邻近整数值之间的偏差基本都在±0.15周之内,与理论分析的0.174 9周接近,可以很准确地单历元确定其模糊度为-183周,相比于其余三组组合具有明显优势,可作为第二组待固定最优模糊度。
|
| 图 3 使用B1频点伪距反算的不同组合浮点模糊度 Fig. 3 Float Ambiguity of Different Combinations Calculated by B1 Psudorange |
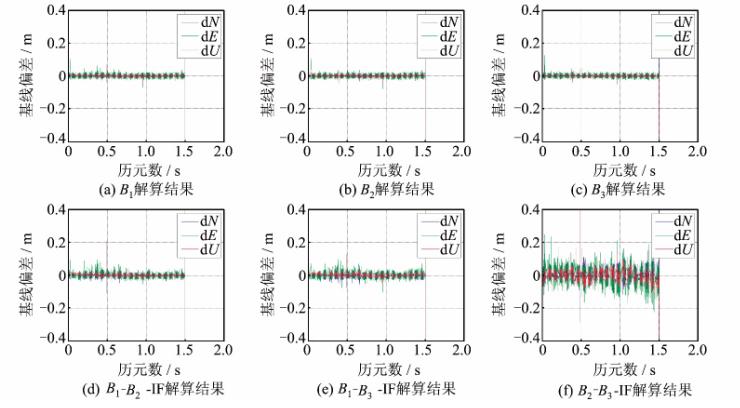
经统计,使用本文方法对该数据进行三频模糊度固定时,3组EWL模糊度单历元固定成功率分别为99.99%、99.81%和99.75%。笔者使用B1、B2、B3以及B1-B2、B1-B3、B2-B3组成的无电离层组合载波(ion-free,IF)进行基线解算,并给出了解算结果在北(N)、东(E)、高(U) 3个方向的偏差如图 4所示。从图 4可以看出,利用北斗三频观测值进行单历元基线解算是可行的,在模糊度正确固定之后,单历元即可实现cm级定位。北斗B1、B2、B3定位精度相当,且普遍在E方向较差,这是由于整个时段只有GEO和IGSO卫星可见,导致卫星在东西方向的几何构型较差所致;无电离层组合放大了观测噪声,导致解算精度较原始观测值低。
|
| 图 4 B1、B2、B3以及B1-B2、B1-B3、B2-B3组成的IF组合解算结果偏差 Fig. 4 Baseline Vector Bias of B1,B2,B3,B1-B2,B2-B3,B2-B3 Phase and Their Ion-Free Combinations |
该数据使用固定汽车上的两台Trimble NetR9天线采集,基线长为0.67m。采用三频单历元进行模糊度解算可得到各组合成功率分别为99.96%、99.96%和95.08%,其单历元定位结果(基线长)如图 5所示。
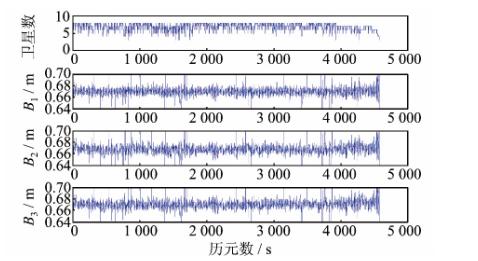
|
| 图 5 使用原始载波解算的基线长 Fig. 5 Baseline Length Calculated by the Three Original Ambiguity Resolved Phase Observations |
可以看到,动态情况下单历元模糊度固定也可达到较高的精度。相对于静态定位而言,动态情况下周跳相对较多,数据预处理难度较大,而单历元模糊度解算无需考虑前后历元之间的周跳问题,可以大大简化数据处理难度,提高定位结果的可靠性。
5 结 语
针对北斗短基线三频数据的“EWL-EWL-EWL”单历元模糊度固定策略是可行的,其关键在于组合的合理选取,载波组合(0,-1,1)、(-1,-5,6)和(-4,0,5)具有较好的误差特性,可作为组合观测值的首选。随着基线长度的增加,电离层、对流层等误差之间的空间相关性也将随之减弱,导致双差残余误差较大。如何寻找合适的组合,并通过合适的方法快速固定中长基线模糊度成为下一步研究的内容。
| [1] | Forssell B, Martin-Neira M, Harrisz R A.Carrier Phase Ambiguity Resolution in GNSS-2[C]. Proceedings of the ION GPS-97, Kansas City, MO, 1997 |
| [2] | Vollath U, Birnbach S, Landau H, et al. Analysis of Three-Carrier Ambiguity Resolution(TCAR) Technique for Precise Relative Positioning in GNSS-2[C]. Global Navigation Satellite Systems, European Symposium, Belgium, 1998 |
| [3] | Hatch R, Jung J, Enge P, et al.Civilian GPS:the Benefits of Three Frequencies[J].GPS Solutions, 2000, 3(4):1-9 |
| [4] | Teunissen P, Joosten P, Tiberius C. A Comparison of TCAR, CIR and LAMBDA GNSS Ambiguity Resolution[C]. Proceeding of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GPS 2002), Portland, Oregon, USA, 2002 |
| [5] | Hatch R. A New Three-Frequency, Geometry-Free Technique for Ambiguity Resolution[C]. Proceedings of ION GNSS, Fort Worth, Texas, 2006 |
| [6] | Feng Y. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-Reduced Virtual Signals[J].Journal of Geodesy, 2008, 82(12):847-862 |
| [7] | Li Bofeng, Shen Yunzhong, Zhou Zebo. Rapid Triple FrequencyAmbiguity Resolution of GNSS Medium Long Baseline[J].Acta Geodaeticaet Cartographica Sinica, 2009, 38(4):296-301(李博峰, 沈云中, 周泽波. 中长基线三频GNSS模糊度的快速算法[J].测绘学报, 2009, 38(4):296-301) |
| [8] | Fan Jianjun, Wang Feixue.A Novel Method of GNSS Three Frequency Ambiguity Resolution(TCAR) Under Short Baseline[J].Acta Geodaeticaet Cartographica Sinica, 2007, 36(1):43-49(范建军, 王飞雪. 一种短基线GNSS的三频模糊度解算(TCAR) 方法[J].测绘学报, 2007, 36(1):43-49) |
| [9] | Ma X, Shen Y. Multipath Analysis of COMPASS Triple Frequency Observations[C]. The International Symposium on GPS/GNSS, Xi'an, China, 2012 |
| [10] | Cocard M, Bourgon S, Kamali O, et al.A Systematic Investigation of Optimal Carrier-Phase Combinations for Modernized Triple-Frequency GPS[J].Journal of Geodesy, 2008, 82(9):555-564 |
 2015, Vol. 40
2015, Vol. 40



