文章信息
- 罗亦泳, 姚宜斌, 黄城, 张静影
- LUO Yiyong, YAO Yibin, HUANG Cheng, ZHANG Jingying
- 基于改进VMD的变形特征提取与分析
- Deformation Feature Extraction and Analysis Based on Improved Variational Mode Decomposition
- 武汉大学学报·信息科学版, 2020, 45(4): 612-619
- Geomatics and Information Science of Wuhan University, 2020, 45(4): 612-619
- http://dx.doi.org/10.13203/j.whugis20180286
-
文章历史
收稿日期: 2018-12-18

2. 武汉大学测绘学院, 湖北 武汉, 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
大型建筑物在建设和运营过程中易受到多种复杂因素的影响,致使建筑物产生不同程度的变形。由于变形过程与变形监测数据获取的复杂性,变形数据具有显著的多尺度、非线性、高噪声特点[1],基于这些特点,如果直接利用变形数据进行变形预测、预警及机理解释难以达到理想的效果,因此,必须开展变形数据特征提取及分析研究,挖掘变形内在规律,为进一步的变形预测、预警及机理解释提供理论基础。
变形特征提取及分析主要包括:①建筑物振动特性参数提取(固有频率、阻尼比参数);②变形数据中具有特殊意义的分量提取,如各种变形影响因素引起的变形分量提取。这些特征的准确提取可有效提高变形预测、健康评价预警及变形机理解释效果。但由于变形过程与监测数据的复杂性,准确提取变形特征难度较大。当前时间序列数据特征提取及分析方法主要有Kalman滤波、小波分析、经验模态分解(empirical mode decomposition,EMD)等[2-4]。若采用传统的Kalman滤波或数据平滑的方法对监测数据在时域内进行处理,则无法表示非平稳变形监测信号的频域特征,存在很大的局限性。小波变换作为一种时频分析方法,在时域和频域上都具有良好的局部化特性,已被广泛用于变形特征的提取[5-8]。但由于小波分解的基函数是固定的,因此小波分解不是自适应的,分解后得到的各个分量失去了本身的物理意义。针对小波变换的局限性,自适应时频分析方法EMD被应用于变形数据去噪及特征提取,去噪及特征提取精度得到一定的改善[9-10]。但由于EMD采用递归筛分剥离运算方式,因此模态混叠、边界效应等一系列问题没有得到很好的解决。综上所述,目前的特征提取方法在精度和可靠性方面还有待提高。
随着信号处理方法的快速发展,Dragomiretskiy等[11]提出一种新的信号多尺度时频分析处理方法——变分模态分解(variational mode decomposition,VMD)。VMD将信号分量的获取过程转移到变分框架内,采用一种非递归的处理策略,通过构造并求解约束变分问题实现原始信号的分解。因此,VMD较EMD、LMD(local mean decomposition)能有效避免模态混叠、过包络、欠包络、边界效应等问题,具有较好的复杂数据分解精度及较好的抗噪声干扰等优点。VMD的这些优势使其在机械故障诊断领域得到较为广泛的应用[12-13]。鉴于VMD算法在多尺度时频分析方面的优点及变形数据的特点,本文利用样本熵、中心频率比和相关系数改进VMD,建立改进变分模态分解(improved variational mode decomposition,IVMD)算法,应用于变形特征提取及分析,以提高算法的实用性及可靠性。并利用仿真信号、桥梁索塔变形数据验证了VMD方法用于变形特征提取及成因分析的有效性及可靠性。
1 VMD基本原理及改进 1.1 VMD原理VMD的分解过程即变分问题的求解过程,在该算法中,本征模态函数(intrinsic mode function, IMF)被定义为一个有带宽限制的调幅-调频函数,VMD算法的功能便是通过构造并求解约束变分问题,将原始信号分解为指定个数的IMF分量。假设欲将一个信号分解为K个IMF分量,则相应的变分问题的构造和求解可概述如下[11, 14]:
1)通过Hilbert变换,得到每个模态分量μk(t)的解析信号,进而得到其单边频谱:
| $ [\delta (t) + \frac{j}{{\pi t}}] \cdot {\mu _k}(t) $ | (1) |
2)对各模态解析信号预估一个中心频率e−jωkt, 将每个模态的频谱调制到相应的基频带:
| $ [(\delta (t) + \frac{j}{{\pi t}}) \cdot {\mu _k}(t){\rm{ }}]{\rm{ }}{e^{ - j{\omega _k}t}} $ | (2) |
3)计算上述解调信号梯度平方L2的范数,估计出各模态信号带宽,受约束的变分问题如下:
| $ \left\{ \begin{array}{l} \mathop {min}\limits_{\{ {u_k}\} ,\{ {\omega _k}\} } \left\{ {\mathop \sum \limits_k \left\| {{d_t}\left[ {\left( {\delta (t) + \frac{j}{{\pi t}}} \right) \cdot {\mu _k}(t)} \right]{e^{ - j{\omega _k}t}}} \right\|} \right._2^2\\ s.t.\mathop \sum \limits_k {u_k} = f \end{array} \right. $ | (3) |
式中,{μk}代表分解得到的K个IMF;{ωk}表示各模态对应的中心频率。
为了求解该约束性变分问题,引入二次惩罚因子α和拉格朗日乘法算子λ(t),将约束性变分问题变为非约束性变分问题。扩展的拉格朗日表达式如下:
| $ L(\{ {u_k}\} , \{ {\omega _k}\} , \lambda ) = \alpha \mathop \sum \limits_k \left\| {{\partial _t}\left[ {\left( {\delta (t) + \frac{j}{{\pi t}}} \right) \cdot {\mu _k}(t)} \right]{e^{ - j{\omega _k}t}}} \right\|_2^2 + \left\| {f(t) - \mathop \sum \limits_k {u_k}(t)} \right\|_2^2 + \left\langle {\lambda (t), f(t) - \mathop \sum \limits_k {u_k}(t)} \right\rangle $ | (4) |
式中,α为二次惩罚因子;λ(t)为拉格朗日乘法算子。其中α可在高斯噪声存在的情况下保证信号的重构精度,通常取拉格朗日算子使得约束条件保持严格性。利用乘法算子交替方向法解决以上无约束变分问题,通过交替更新
VMD对时间序列数据进行特征提取时,分解模态数K值的确定是关键。若K小于被处理信号中有用成分的个数,会造成数据分解不充分;若K大于被处理信号中有用成分的个数,则会出现过分解现象,产生虚假分量。VMD算法在求解中心频率及模态分量的过程中,中心频率的初值设定对VMD分解结果的影响较大,当前VMD研究较少考虑该因素。
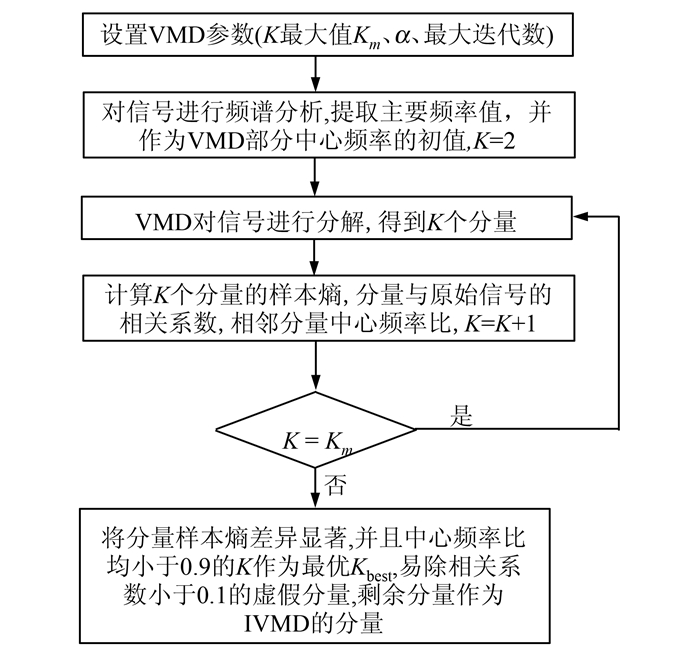
针对VMD的K值确定问题,本文利用样本熵、中心频率比及相关系数合理确定VMD的最优K值(用Kbest表示),较好地解决了VMD算法的欠分解及过分解现象,并有效剔除虚假分量。样本熵能有效地表示时间序列的复杂性,越复杂的时间序列对应的样本熵越大[15]。当VMD较好地提取到复杂混合信号中包含的有效分量信号时,有用的VMD分量对应的样本熵值较小,并且相邻分量的样本熵有显著差异,噪声分量的熵值通常相对较大。当VMD出现过分解现象时,部分相邻分量的样本熵相近。因此,可利用样本熵的以上特点,提取有用VMD分量及分析是否存在过分解问题。当VMD出现过分解时,VMD分量的中心频率接近。因此,可利用相邻中心频率比作为过分解的一个指标,通常将中心频率比大于0.9作为过分解判定标准。利用相关系数可有效分析分量与原始信号的相关性,进而可利用相关系数判定VMD分量是否为有用分量及噪声分量,通常将相关系数小于0.1作为虚假分量及噪声分量剔除标准。对原始信号进行频谱分析,提取能值较为显著的频率作为VMD算法的部分中心频率初值,可提高VMD的分解效率及精度。基于以上方法,本文建立的IVMD算法工作流程如图 1所示。
|
| 图 1 IVMD建模流程图 Fig. 1 Flowchart of IVMD Algorithm Modeling |
为了验证IVMD算法的数据特征提取能力及其K值确定的有效性,设计了两种仿真信号进行验证。仿真信号1验证IVMD对加噪声间断信号的特征提取能力,仿真信号2模拟变形数据,验证IVMD在噪声干扰下对周期性变化成分的提取能力。将IVMD分解结果与小波分解(wavelet decomposition,WD)算法、EMD分解进行对比分析,验证IVMD算法特征提取的有效性及可靠性。
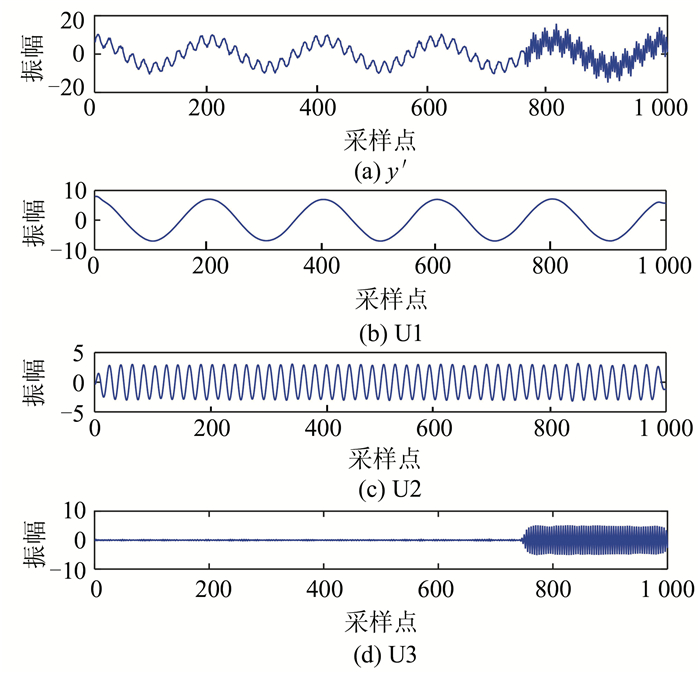
2.1 仿真信号1的VMD分解及分析采用式(5)合成信号y,信号的采样频率为1 000 Hz,并在合成信号上添加信噪比为8的高斯白噪声构成仿真信号1(用y'表示)。y'包括间断信号成分y3,并且包含噪声干扰,可有效验证特征提取方法的抗噪声干扰及间断成分提取能力,具体如图 2所示。
|
| 图 2 真信号1及IVMD分解结果 Fig. 2 Simulation Signal 1 and IVMD Decomposition Results |
| $ \left\{ \begin{array}{l} y1{\rm{ }} = {\rm{ }}7{\rm{cos}}(10\pi t)\\ y2{\rm{ }} = {\rm{ }}3{\rm{sin }}(100\pi t)\\ y3{\rm{ }} = \left\{ {_{5{\rm{sin}}(500\pi t - 50\pi ), t > {\rm{ }}0.75}^{{\rm{ }}0{\rm{ }}, {\rm{ }}t \le 0.75}} \right.\\ y = y1{\rm{ }} + y2{\rm{ }} + y3 \end{array} \right. $ | (5) |
确定Kbest=3,IVMD的分量为{U1, U2, U3},如图 2所示。各分量对应的频谱如图 3所示。为了进一步验证IVMD算法特征提取的精度及可靠性,分别用EMD、WD对信号y'进行多尺度分解,比较3种特征提取方法的优劣。分别计算3种分解方法提取的有效分量与其理论值的相关系数R和均方根误差(root mean square error,RMSE),可定量分析算法的分解精度,具体数据见表 1。

|
| 图 3 IVMD分量频谱图 Fig. 3 Spectrogram of IVMD Component |
| 分解方法 | 对应模态分量 | R | RMSE |
| IVMD | y1—U1 | 0.999 | 0.166 |
| y2—U2 | 0.995 | 0.204 | |
| y3—U3 | 0.992 | 0.220 | |
| EMD | y1—imf4 | 0.997 | 0.346 |
| y2—imf2 | 0.877 | 1.036 | |
| y3—imf1 | 0.982 | 0.335 | |
| WD | y1—a3 | 0.924 | 2.056 |
| y2—d3 | 0.283 | 2.035 | |
| y3—d2 | 0.985 | 0.281 |
由图 2可知,IVMD分解结果的端点效应得到有效抑制。各分量的频谱图显示,在噪声的干扰下,IVMD分解结果没有出现模态混淆现象,并且各分量的振幅、频率和理论值非常接近,表明IVMD方法具有较高的特征提取精度及可靠性,并且具有较好的抗噪能力。利用EMD分解信号y',产生8个模态分量,理论上只有3个模态分量出现明显的模态混淆现象。通过将各模态分量与y1、y2、y3对比发现,y1、y2、y3分别对应EMD的imf4、imf2、imf1分量,模态混淆问题严重,出现多个虚假模态,并且端点效应明显,导致RMSE指标较差。小波分析选取正交性较好的db10小波进行3层分解,分解层数与IVMD保持一致。通过比较分析,y1、y2、y3与小波的a3、d3、d2分量对应,并且a3、d3分量的频谱图出现多个峰值,表明特征分量提取不充分。由表 1可知,IVMD的R指标略优于EMD,显著优于WD方法;IVMD各分量的RMSE指标显著优于EMD与WD方法,在噪声的干扰下,EMD与WD方法的数据分解精度受到较大影响。因此,表 1结果验证了IVMD比EMD、WD方法具有更好的特征提取能力,有效避免了端点响应、模态混淆问题,具有较好的抗噪能力,能准确提取信号中包含的有效成分,并且较为精确地提取到分量的振幅及频率特征信息。
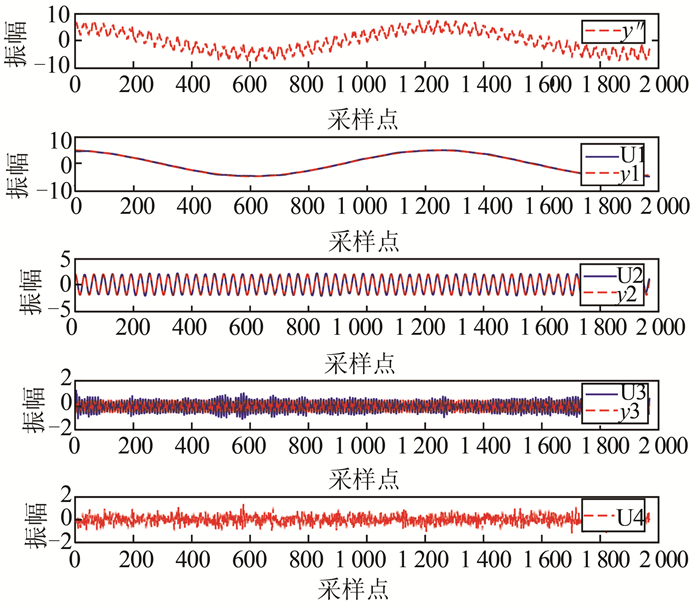
2.2 仿真信号2分解及分析采用式(6)合成信号y,采样频率为30 Hz,并添加信噪比为8的高斯白噪声θ生成仿真信号y'',信号波形如图 4所示。y''包含强度较弱的信号y3,在强噪声干扰下,大大提高了弱信号y3的提取难度,可有效模拟并检验IVMD对强噪声背景下变形数据中的弱变形信号提取能力,具体信号见图 4。IVMD确定的最优分解Kbest=4,并获得y''信号的分解分量{U1, U2, U3},利用相关系数判定U4为噪声分量,分解结果见图 4。
|
| 图 4 仿真信号2及IVMD分解结果 Fig. 4 Simulation Signal 2 and IVMD Decomposition Results |
| $ \left\{ \begin{array}{l} y1{\rm{ }} = {\rm{ }}5{\rm{cos}}(2\pi t/40{\rm{ }})\\ y2{\rm{ }} = {\rm{ }}2{\rm{cos}}(2\pi t)\\ y3{\rm{ }} = {\rm{ }}0.5{\rm{cos}}(7\pi t)\\ y = y1{\rm{ }} + y2{\rm{ }} + y3 \end{array} \right. $ | (6) |
由图 4可知,IVMD准确地提取了y1、y2成分,并且U1、U2与理论值y1、y2差异非常小。U1、U2、U3分量端点效应影响非常小,没有出现明显的模态混淆现象。IVMD提取到弱信号U3成分,在强噪声θ的干扰下,增加了U3与理论值y3之间的差异,其R指标为0.931,RMSE指标为0.109 8,但总体效果较好。图 5为弱信号分量U3的频谱图。由图 5可知,提取的弱信号U3的振幅、频率与其理论值较为接近,差异主要由于y3信号较弱并且受到强噪声干扰。

|
| 图 5 弱信号分量U3的频谱图 Fig. 5 Spectrogram of Weak Signal Component U3 |
利用EMD、WD分别分解y''信号,其R指标、RMSE指标如表 2所示。由表 2可知,IVMD的R指标、RMSE指标均优于EMD、WD,对于弱信号y3,IVMD受噪声干扰较小,提取效果明显好于EMD、WD,验证了IVMD对强噪声干扰下的弱信号提取能力。
| 分解方法 | 对应模态分量 | R | RMSE |
| IVMD | y1—U1 | 0.999 | 0.082 6 |
| y2—U2 | 0.996 | 0.114 2 | |
| y3—U3 | 0.931 | 0.109 8 | |
| EMD | y1—imf7 | 0.998 | 0.206 |
| y2—mf3 | 0.913 | 0.586 | |
| y3—imf2 | 0.698 | 0.286 | |
| WD | y1—a3 | 0.928 | 1.435 |
| y2—d3 | 0.374 | 3.585 | |
| y3—d2 | 0.809 | 0.214 |
变形特征提取是将建筑物的变形特征信息从含噪数据中挖掘出来,是提高变形预测、预警精度的有效途径。以苏通大桥为例,分析IVMD方法对变形特征提取的有效性。苏通大桥位于江苏省东部的南通市和苏州(常熟)市之间,该桥梁结构为双塔双索面斜拉桥,于2008年6月30日建成通车,全长8 146 m,主跨长1 088 m,主索塔高300.4 m,。大桥位于长江下游,每年都会经历长时间的台风期,昼夜温差比较大,各种因素对桥梁的变形产生了较大影响。本文选取北塔X坐标方向(南北方向)采样频率为1 Hz的4 500个全球定位系统(Global Positioning System,GPS)变形监测数据作为案例1。由奈奎斯特定律可知,1 Hz的GPS桥梁索塔变形数据可有效分析0~0.5 Hz的桥梁震动特性,可用于提取桥梁的固有频率及阻尼比特性。选取北塔X坐标方向30 s采样率的14 400个GPS变形监测数据作为案例2,用于提取由温度和其他外界因素引起的变形分量。为避免直流分量干扰分解,实验前先对所有数据进行零均值化处理。
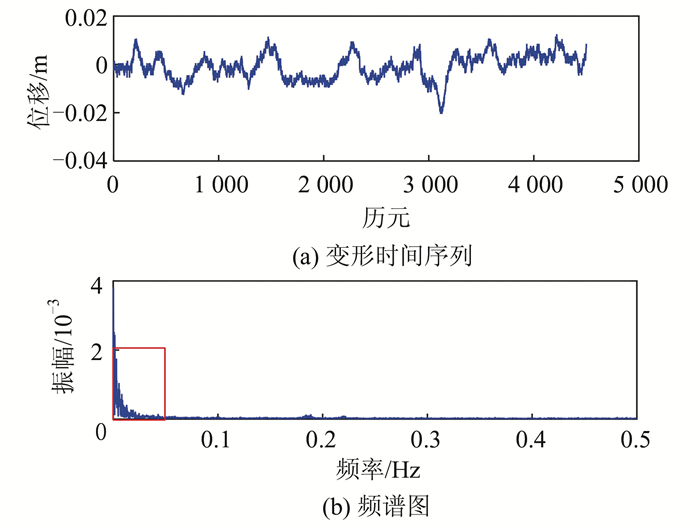
3.1 案例1(桥梁动态特性提取:固有频率、阻尼比参数的提取)固有频率、阻尼比参数是桥梁健康诊断与预警的核心指标,是变形特征的关键参数。案例1以苏通大桥北索塔X方向的变形时间序列为例,提取固有频率(也叫自振频率)、阻尼比参数,X方向的变形时间序列如图 6(a)所示,对应的频谱图如图 6(b)所示。从图 6(b)中可以看到,GPS监测序列中周期成分的频率主要集中在低频部分,其频率范围为0~0.05 Hz(红框所示),其他频段无明显突出峰值,说明桥梁振动信号完全被噪声所湮没,从原始信号中无法直接分析桥梁的振动特性。
|
| 图 6 案例1中X方向变形时间序列及其频谱图 Fig. 6 X Deformation Time Series and Its Spectrogram of X-Direction in Case 1 |
IVMD对GPS变形监测数据进行分解,得到3个变形分量,具体分解结果见图 7。由图 7可知,IVMD将变形数据分解成3个分量,并且U1、U2、U3的频率不存在重复,有效避免了模态混淆问题。U1的频率范围在0~0.05 Hz,属于低频部分,并且能值较高。U2主要包括静态、准静态和多路径效应3部分,主要由风荷载、环境温度变化及观测环境引起的多路径效应引起,其频率范围在0.12~0.23 Hz,并且频谱在0.17 Hz附近有明显的峰值。根据高层建筑结构的基本自振规律(自振周期单位为s,范围为[0.05~0.1]·N,N是建筑物的层数)可计算苏通大桥索塔(高约306 m,N≈102)的自振频率为0.1~0.2 Hz[7],因此U2属于桥梁自振部分。U3频率在0.26~0.4 Hz,并且能量较小,频谱没有明显的峰值,因此属于随机噪声。

|
| 图 7 案例1中X方向IVMD分解结果及对应分量的频谱图 Fig. 7 IVMD Decomposition Results and Corresponding Spectrograms of X-Direction in Case 1 |
U2属于自振部分,从中提取固有频率及阻尼比是桥梁健康诊断及预警的关键。利用ITD(the Ibrahim Time Domain Technique)技术可有效估算U2分量的固有频率及阻尼比,确定固有频率为0.17 Hz,阻尼比为2.15%,和当前相关的研究成果较为吻合,验证了IVMD方法提取桥梁固有频率与阻尼比的有效性。当数据采样频率更好时,可有效提取更多阶次与方向的固有频率与阻尼比参数,可用于桥梁健康诊断及预警。
3.2 案例2(变形分量提取及成因分析)桥梁的变形分量提取及成因分析可用于变形预测及机理解释。案例2中采用北塔X方向5 d的GPS变形监测时间序列,如图 8所示。由图 8可知,变形数据具有显著日周期及趋势项。为了准确提取日周期及趋势项,并且保证其光滑性,IVMD的K=15, 将U1作为日周期及趋势项,其频谱峰值在1 d附近,U1分量曲线图如图 9所示。U1为桥梁受温度及日照影响的变形分量,显示出显著的日周期。当太阳照射大桥南面时,南面混凝土与北面混凝土温差不断增大,这种温差将导致大桥南面混凝土膨胀,北面混凝土收缩,从而使索塔产生扭转变形。进一步观察位移曲线,可发现位移变化的峰值出现在每天16:00左右(图 9中红圈标示),而气温一般在14:00达到最高。产生滞后效应的原因是由于桥梁体积庞大,温度在桥梁内部传递需要一段时间。因此,IVMD能有效提取到桥梁变形的温度分量。

|
| 图 8 X方向变形时间序列 Fig. 8 Deformation Time Series of X-Direction |

|
| 图 9 U1分量曲线图 Fig. 9 U1 Component Curve |
为了进一步分析多路径效应及水流冲击、风荷载(脉动风)等的影响,分别截取前3天IVMD的U2分量,如图 10所示。第1天与第2天的U2分量之间的相关性为0.72,第2天与第3天的U2分量之间的相关性为0.76。根据多路径效应具有周日重复性的特征,即在环境变化不大的前提下,相邻两天的多路径效应相关性较大。因此,U2分量主要是由多路径效应引起。其余分量之间的相关性都小于0.05,并且频率较低,可能主要受到水流冲击、风荷载(脉动风)等环境的综合影响,导致桥梁产生这些变形分量。

|
| 图 10 U2分量前3天曲线图 Fig. 10 U2 Component Curve for the First Three Days |
本文利用样本熵、中心频率比及相关系数确定VMD的最优K值,建立IVMD算法。两个仿真信号特征提取实例表明,在噪声干扰下,IVMD能有效地提取到间断信号分量及弱信号分量,并且提取的所有分量和其理论值十分接近,端点效应及模态混淆问题得到有效抑制,验证了IVMD用于数据特征提取具有较好的精度。
IVMD算法从GPS变形监测数据中能有效提取桥梁索塔振动特性(固有频率、阻尼比),并与相关文献的研究结果吻合度较好。IVMD较为准确地提取了桥梁索塔温度变化、多路径效应及其余变形分量等特征信息,证实了IVMD用于变形特征提取及分析具有较好的有效性及可靠性。
| [1] |
Zhang Zhenglu, Pan Guorong, Li Guangyun. Engineering Surveying[M]. Wuhan: Wuhan University Press, 2005. (张正禄, 潘国荣, 李广云. 工程测量学[M]. 武汉: 武汉大学出版社, 2005. )
|
| [2] |
Lin L, Hongbing J. Signal Feature Extraction Based on an Improved EMD Method[J]. Measurement, 2009, 42(5): 796-803. |
| [3] |
Kuang Cuilin, Dai Wujiao. Measurement of WindInduced Vibration of Tall Buildings Using GPS and Wavelet Application[J]. Geomatics and Information Science of Wuhan University, 2010, 35(9): 1024-1028. (匡翠林, 戴吾蛟. GPS监测高层建筑风致振动变形及小波应用[J]. 武汉大学学报·信息科学版, 2010, 35(9): 1024-1028. ) |
| [4] |
Wang Xiaolei, Zhang Qin, Zhang Shuangcheng. Periodic Oscillation Analysis of GPS Water Vapor Time Series Using Combined Algorithm Based on EMD and WD[J]. Geomatics and Information Science of Wuhan University, 2018, 43(4): 620-628. (王笑蕾, 张勤, 张双成. 基于EMD和WD联合算法的GPS水汽时间序列的周期性振荡分析[J]. 武汉大学学报·信息科学版, 2018, 43(4): 620-628. ) |
| [5] |
Li Zongchun, Deng Yong, Zhang Guanyong, et al. Deformation Measurement of Abnormal Data in the Wavelet Transform to Determine the Best Series[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 285-288. (李宗春, 邓勇, 张冠宇, 等. 变形测量异常数据处理中小波变换最佳级数的确定[J]. 武汉大学学报·信息科学版, 2011, 36(3): 285-288. ) |
| [6] |
Gao J X, Hong H U, Liu F, et al. Signal Extraction for GPS Deformation Monitoring in Mining Survey[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(12): 3949-3954. DOI:10.1016/S1003-6326(14)63555-X |
| [7] |
Xu Chang, Yue Dongjie. Ambient Vibration Test of High Pylon Based on RTK-GPS Technology[J]. Journal of Vibration and Shock, 2010, 29(3): 134-210. (许昌, 岳东杰. 基于RTK-GPS技术的高索塔振动试验与分析[J]. 振动与冲击, 2010, 29(3): 134-210. DOI:10.3969/j.issn.1000-3835.2010.03.033 ) |
| [8] |
Mao Jianxiao, Wang Hao, Xun Zhixiang. Comparison Study on Modal Parameter Identification of Large Span Cable Stayed Bridge with Time-Frequency Method[J]. Journal of Tongji University (Natural Science Edition), 2016, 44(7): 996-1001. (茅建校, 王浩, 荀智翔. 大跨度斜拉桥模态参数识别时频方法对比研究[J]. 同济大学学报(自然科学版), 2016, 44(7): 996-1001. ) |
| [9] |
Xu Jia, Huang Shengxiang, Ma Fenghai. The Dynamic Characteristics Analysis for the Large Bridge Based on the Improved Hilbert-Huang Transformation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(7): 801-805. (徐佳, 黄声享, 麻凤海. 基于改进HHT理论的大型桥梁动态特性分析[J]. 武汉大学学报·信息科学版, 2010, 35(7): 801-805. ) |
| [10] |
Lu Chenlong, Kuang Cuilin, Yi Zhonghai, et al. Singular Spectrum Analysis Filter Method for Mitigation of GPS Multipath Error[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 924-931. (卢辰龙, 匡翠林, 易重海, 等. 奇异谱分析滤波法在消除GPS多路径中的应用[J]. 武汉大学学报·信息科学版, 2015, 40(7): 924-931. ) |
| [11] |
Dragomiretskiy K, Zosso D. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 |
| [12] |
Wu Yingjie. Research on Fault Diagnosis of Wind Turbine Transmission System Based on Variational Mode Decomposition[D]. Beijing: North China Electric Power University, 2016 (武英杰.基于变分模态分解的风电机组传动系统故障诊断研究[D].北京: 华北电力大学, 2016)
|
| [13] |
Jia Yafei, Zhu Yongli, Wang Liuwang, et al. Feature Extraction and Classification of Partial Discharge Signals in Transformer Insulation Based on VMD and Multi-Scale Entropy[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 208-217. (贾亚飞, 朱永利, 王刘旺, 等. 基于VMD和多尺度熵的变压器内绝缘局部放电信号特征提取及分类[J]. 电工技术学报, 2016, 31(19): 208-217. DOI:10.3969/j.issn.1000-6753.2016.19.022 ) |
| [14] |
Tang Guiji, Wang Xiaolong. Paramater Optimized Variational Mode Decomposition Method with Application to Incipient Fault Diagnosis of Rolling Bearing[J]. Journal of Xi'an Jiaotong University, 2015, 49(5): 73-81. (唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报, 2015, 49(5): 73-81. ) |
| [15] |
Xie H B, He W X, Liu H. Measuring Time Series Regularity Using Nonlinear Similarity-based Sample Entropy[J]. Physics Letters A, 2008, 372(48): 7140-7146. DOI:10.1016/j.physleta.2008.10.049 |
 2020, Vol. 45
2020, Vol. 45


