文章信息
- 赵洪臣, 周兴华, 彭聪, 刘永学, 张家发, 陈义兰
- ZHAO Hongchen, ZHOU Xinghua, PENG Cong, LIU Yongxue, ZHANG Jiafa, CHEN Yilan
- 一种去除遥感影像混合噪声的集成BM3D方法
- An Integrated BM3D Method for Removing Mixed Noise in Remote Sensing Image
- 武汉大学学报·信息科学版, 2019, 44(6): 925-932
- Geomatics and Information Science of Wuhan University, 2019, 44(6): 925-932
- http://dx.doi.org/10.13203/j.whugis20170188
-
文章历史
收稿日期: 2018-05-25

2. 国家海洋局南海调查技术中心, 广东 广州, 510300;
3. 南京大学地理与海洋科学学院, 江苏 南京, 210023;
4. 中国南海研究协同创新中心, 江苏 南京, 210023
2. South China Sea Marine Survey and Technology Center, SOA, Guangzhou 510300, China;
3. School of Geographic and Oceanographic Sciences, Nanjing University, Nanjing 210023, China;
4. Collaborative Innovation Center for the South China Sea Studies, Nanjing 210023, China
遥感传感器系统存在一定的缺陷,对地观测条件具有一定的限制,因此电磁波信号采集和传送过程中会产生噪声[1]。噪声融入到影像像元的辐射亮度值中降低影像质量,势必会对遥感影像定量化过程带来阻碍。影像去噪的目的是减少无关噪声,提高影像质量,同时尽可能保留原始影像的有效信息[2-3]。
影像去噪方法多种多样,基于概率论、统计学、偏微分方程、线性非线性滤波和波谱及多尺度分析等不同理论的模型相继被提出[4]。其中,均值滤波通过对邻域均值平滑去除异常噪声,该法较为简单;中值滤波由Tukey提出,通过提取邻域中值以去除奇异噪声,对脉冲噪声尤为有效;维纳滤波是最小均方差准则下平稳过程的最佳滤波器,但会受自然影像复杂非平稳的限制[5];高斯低通滤波在影像频率域内处理高频信号以达到去噪的目的。以上方法虽然都能有效去除噪声,但会导致边缘失真,造成严重的影像模糊。基于小波分解的去噪方法在小波变换域上对高频噪声使用软硬阈值处理,由于具有多尺度、多分辨分析和时频局部化等特点,与其他传统去噪方法相比,在信噪分离方面具有独特的优越性[6]。但噪声较多时多层小波分解会损失影像分辨率,仍无法避免细节的丢失。
近年来,稀疏表达的影像去噪方法由于具有较好的去噪性能和细节保留特性,颇受关注[7]。Muresan等提出局部影像块的自适应主成分(principal components,PC)算法,使用PC基稀疏重建影像,可产生高结构化的影像模式,但正确的PC基的获取不可避免地受到噪声的影响,且该法计算量较大[8];Elad等提出K-SVD(K-means singular value decomposition,K-SVD)法,它是一种基于字典学习的稀疏去噪方法,假设影像结构要素可以由一组超完备字典原子组合表达,而随机噪声则不可,通过使用字典原子重构图像,去除冗余,达到去噪的目的[9],虽然去噪效果较好,但由于字典学习的迭代和更新,导致计算量较大,时间成本高。考虑到以上问题,Dabov等提出了一种更加高效且能获得较高稀疏性的变换域稀疏表达方法,即BM3D(block matching and 3D filtering)法[4]。BM3D利用“组块”之间的相关性,通过联合滤波实现影像的高度稀疏化,去噪性能较好,且具有更高的运行效率,与其他方法相比更具优势。
但实际的遥感影像往往具有不止一种噪声,而单一方法去除混合噪声往往无法达到理想效果,因此集成(混合)去噪的方法被很多学者提出。袁文成等提出一种中值滤波和维纳滤波集成去噪方法(median-wiener filter MW),同时融合了图像边缘以减少细节丢失[10]。该法对去除高斯、脉冲混合噪声比单一滤波器更好;Dong等则提出一种Bior小波变换与中值滤波集成去噪法(Bior wavelet-transform and median filter, BWM),发挥了小波和中值滤波各自的优势,对去除混合噪声具有很好的性能[11];朱建军等针对小波、中值两层滤波会有残留噪声的问题,提出一种小波变换、中值滤波和维纳滤波三层滤波组合的去噪方法(wavelet bayes shrink-median-wiener filter, WMW),并增加边缘融合以避免多次滤波造成细节失真[12]。上述方法虽然在去除混合噪声方面都有较好的表现,但仍有待改进之处,如小波法的保真性在低梯度区无效,边缘融合中使用高斯拉普拉斯算子提取边缘虽然能去除边缘残留噪声,但是算子参数的调优较麻烦,过大则无法获得有效边缘,过小则有噪声残留。
结合图像去噪近些年的发展,将稀疏表达方法用于集成去噪是一种新思路,不仅可以发挥稀疏去噪的优势,而且可以避免单一模型去噪的缺陷,在实现高效去噪目标方面具有较大的潜力。鉴于BM3D法在去除高斯噪声方面具有较大的优势,能更好地兼顾噪声去除和细节信号保留,且具有较高的运行效率,优于同类方法;但对含有脉冲噪声的混合噪声去除效果有一定的局限性,混合噪声去除效果受制于先验噪声含量输入值的大小,输入值不当常会导致脉冲噪声无法去除,且有一定的细节信号丢失。为充分利用BM3D去除高斯噪声的优势,本文对BM3D法进行改进,提出一种集成BM3D策略,通过混合噪声去除实验,验证了该算法的有效性,以期为影像混合噪声去除提供新的方法借鉴。
1 BM3D法原理 1.1 基本原理BM3D法是一种在转换域中加强稀疏表达的去噪方法。由于自然影像在不同空间位置上存在相似影像块(如相同区域、边界、纹理及相同的平滑密度梯度等),为达到更好的去噪效果,BM3D算法较多地顾及了影像中的纹理和边缘信息。通过将二维图像块根据某种相似性度量,构建(分组)三维组,并通过三维组的联合滤波实现图像的稀疏表达。具体分为基本估计和最终估计两部分。
1.1.1 基本估计1) 块匹配分组:搜索与当前参考块相似度高的匹配块,将匹配结果与参考块堆叠构建三维组,分组的目的是为了利用更高维度的滤波器挖掘组块间的潜在相似性,以便估计真实信号。
2) 联合滤波(硬阈值滤波):对所堆叠形成的三维组应用3D线性变换,通过收缩系数的硬阈值滤波实现噪声去除,随后应用反3D线性变换以产生对所有分组块的估计,并将其估计值返回至块的初始位置。
3) 整合。由于协同滤波后的估计块往往有重叠,因此对重叠区进行加权平均的信息整合,即通过加权平均所有重叠块的预估值来计算真实图像的基础估计。
1.1.2 最终估计基于基本估计,执行改进的分组方法和经验维纳滤波。
1) 块匹配分组。在基础估计中使用块匹配搜索与当前参考块相似的匹配块的位置,依据它们的位置形成两个组(三维组),其中,两个组分别来自噪声图像和基础估计图像。
2) 联合滤波(经验维纳滤波)。在两个组上应用3D线性变换,能量谱以基础估计所得为真值,对噪声进行经验维纳滤波。通过三维变换域中系数收缩实现反3D线性变换生成所有分组块的估计值,并将其返回至块的初始位置。
3) 整合。通过加权平均聚合所有局部估计值来计算真实图像的最终估计。
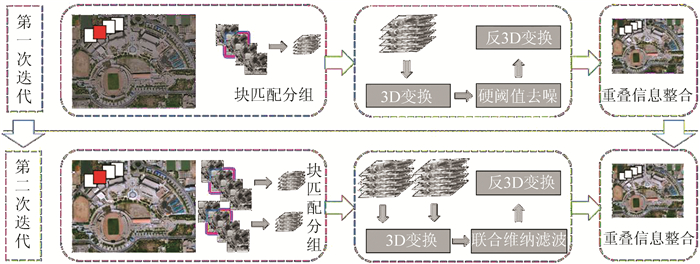
1.2 算法实现BM3D算法的具体实现包括块匹配、联合滤波和信息整合3个步骤的两次迭代(见图 1)。第一次迭代依次进行块匹配分组、3D变换、硬阈值去噪和反3D变换产生预估值,通过重叠信息整合得到基本估计;第二次迭代根据基本估计影像块匹配产生分别对应噪声图和基本估计的两对相似组,联合滤波除3D变换和反3D变换外,使用了基本估计组对噪声组进行维纳滤波,再通过重叠信息整合得到最终估计。
|
| 图 1 BM3D方法流程 Fig. 1 Flowchart of BM3D |
集成BM3D法的目的在于充分利用BM3D去除高斯噪声的优势,同时尽可能多地恢复去噪过程中丢失的图像细节。该集成去噪策略利用了小波去噪法处理高频部分以去除噪声,并保留低频信号的原理,首先使用BM3D和中值滤波两级集成去除混合噪声,然后对去除的高频部分通过小波阈值法、中值滤波和维纳滤波三级级联式集成提取高频中的有效信号。集成BM3D去噪的结果融合了上述两部分内容,以保证去除噪声的同时尽量保留细节的目的。
2.1.1 集成BM3D算法假设无噪影像为Y,含有混合噪声的影像为Y′,可表示为:
| $ Y^{\prime}=\operatorname{pul}(Y+G) $ | (1) |
式中,G为高斯噪声;pul(*)表示影像被脉冲噪声污染。
首先,利用BM3D和中值滤波两级联合去除混合噪声,即
| $ D N=D p\left(\mathrm{BM} 3 \mathrm{D}\left(Y^{\prime}\right)\right) $ | (2) |
式中,DN为去噪后的低频信号;BM3D(*)为利用BM3D法去除Y′中的高斯噪声;Dp(*)表示脉冲噪声滤波器。
其次,利用原始含噪影像与去噪影像差值运算,得到噪声影像的高频部分Hi,如式(3)所示。由于差值结果很多值偏小,因此对差值结果作归一化拉伸处理,以提高对比度,如式(4)所示。
| $ H i=Y^{\prime}-D N $ | (3) |
| $ H i^{\prime}=\left\{\begin{array}{l}{\frac{(H i+H i_{|\min |}Y_{\max}}{H i_{\max }-H i_{\min }}, H i_{\min } \leqslant 0} \\ {\frac{\left(H i-H i_{|\min| }\right) Y_{\max }}{H i_{\max }-H i_{\min }}, H i_{\min }>0}\end{array}\right. $ | (4) |
式中,Hi′为拉伸后的高频影像矩阵;Himin为Hi所有组成元素中的最小值;Himax为Hi所有组成元素中的最大值;Hi|min|表示Himin的绝对值;Ymax为由Y的辐射分辨率(灰度级)决定的最大值(如8位为255)。然后,利用式(5)从拉伸后的高频信息中提取有效信号。
| $ S g=\operatorname{Wien}\left(D p\left(D g\left(H i^{\prime}\right)\right)\right) $ | (5) |
| $ \hat{Y}=S g^{\prime}+D N $ | (6) |
式中,Wien(*)为维纳滤波器;Dg(*)为高斯噪声滤波器;Sg为提取的有效信号。
最后,按照式(4),将Sg和Sg′分别替换为式(4)中的Hi′和Hi,由于式(4)中分母和Ymax均为常量,因此通过此方式可将Sg作反归一化的去拉伸处理得到Sg′,并利用式(6)将Sg′与DN融合,得到最终的去噪影像估计结果。
2.1.2 集成BM3D法具体实现集成BM3D法的实现中,Dp(*)脉冲滤波器选择一种自适应中值滤波,自适应中值滤波根据局部均值和方差判断当前像元是否为椒盐等脉冲噪声,若像元值与邻域均值之差大于邻域方差的某个算数级倍数,则认为该点为脉冲噪声,且仅对确定为脉冲噪声的点滤波处理,因此在一定程度上弥补了传统中值滤波将所有像元参与滤波而丢失边缘、纹理等细节的缺陷。Dg(*)高斯噪声滤波器的选择以高质量的高斯噪声去除法为佳,因此小波阈值法[13-14]和基于字典学习的K-SVD法均可,但K-SVD运行效率较低,尤其当字典原子数和迭代次数设置较大时,运行效率呈几何级数递减,因此这里选用小波法。Wien(*)选用自适应维纳滤波[15]。自适应维纳滤波根据公式
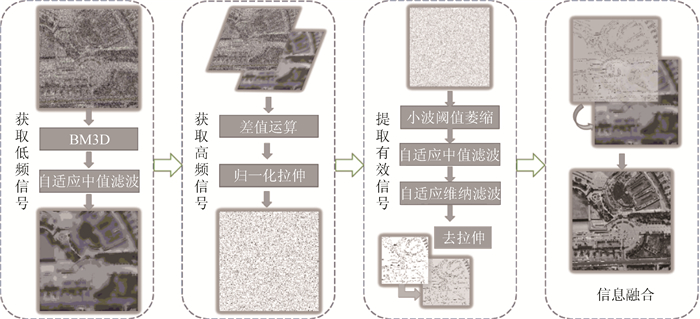
算法实现步骤如下(见图 2):
|
| 图 2 集成BM3D法流程图 Fig. 2 Flowchart of Assembled BM3D |
1) 使用BM3D对原始混合噪声影像去噪;
2) 使用自适应中值滤波对步骤1)结果影像去噪;
3) 将原始噪声影像与2)结果影像差值进行运算,并归一化拉伸处理得到高频信号;
4) 使用小波阈值收缩削去3)高频信号的高斯噪声;
5) 使用自适应中值滤波滤除4)结果信号的脉冲噪声;
6) 使用维纳滤波进一步去除5)结果信号的残余噪声;
7) 反归一化6)结果信号,得到从高频信号中提取出的有效信号;
8) 利用加法运算,融合2)低频信号和7)提取的高频信号。
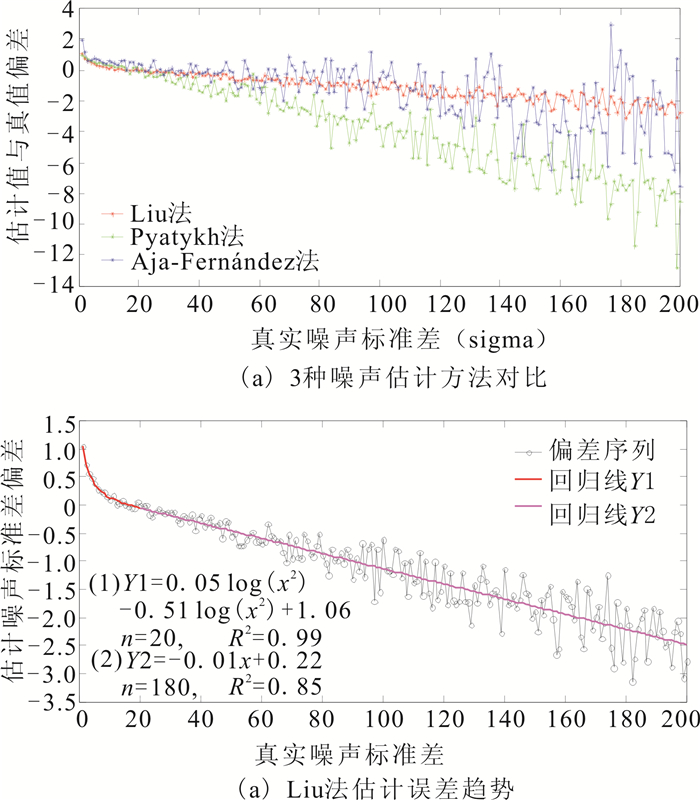
2.2 先验噪声估算BM3D以含噪影像的先验噪声含量(噪声标准差)作为输入参数,然而噪声含量一般无法提前获知,因此需使用某种方法估计影像的噪声含量。Aja-Fernández等提出一种使用影像样本方差分布众数估计噪声含量的方法,能有效估算加性噪声和乘性噪声含量级别[16];Pyatykh等则提出一种基于影像块主成分分析(principal component analysis, PCA)的噪声估计方法,对含有纹理的影像估算结果较为准确[17];而Liu等则提出一种对影像弱纹理块PCA分析以估算噪声的方法,具有较好的准确性[18]。以上方法虽都能计算出准确的高斯噪声标准差,然而其误差随着噪声含量的增加逐渐增大,且前两种方法随着噪声含量增加,出现严重震荡,鲁棒性较差,如图 3(a)所示。
|
| 图 3 估算噪声标准差偏差变化趋势及Liu法改进方式 Fig. 3 Tendency of the Estimated Gaussian Noise Level and Modifying Method Proposed by Liu |
观察发现,3种方法估计误差均随真实噪声含量增加呈由正及负的递减趋势,其中Liu法鲁棒性最佳,且变化趋势有明显的对数或线性变化关系。因此本文利用该变化关系对Liu法进行改进(以下简称M-Liu法)。通过线性回归,将Liu法估计误差变化趋势拟合为一个分段函数,如图 3(b)所示,因此使用式(7)对Liu法进行改进。
| $ \hat{s}=\left\{\begin{array}{l}{s-0.05 \log ^{2} x+0.51 \log x-1.06, x \leqslant 20} \\ {s+0.01 x-0.22, x>20}\end{array}\right. $ | (7) |
式中,
为验证集成BM3D法的有效性,选用标准图像Lena和Peppers,分别加入遥感影像中常见的两种混合噪声类型:0.01/0.000 5和0.05/0.001,进行去噪实验。混合噪声参数前者表示高斯噪声标准差(sigma),后者表示脉冲噪声密度(dens)。为充分说明该方法的效果,分别使用BM3D法、TV(total variation)法[19]、WMW法、BWM法、MW法和K-SVD与自适应中值滤波集成去噪的方法(以下简称KSVD-Med法)进行去噪实验,并与本文提出的集成BM3D法对比。定量分析指标选用峰值信噪比(peak signal to noise ration, PSNR)[20]和均方差(mean square error, MSE)[21]。PSNR越大,MSE越小,表示去噪图像质量越好。
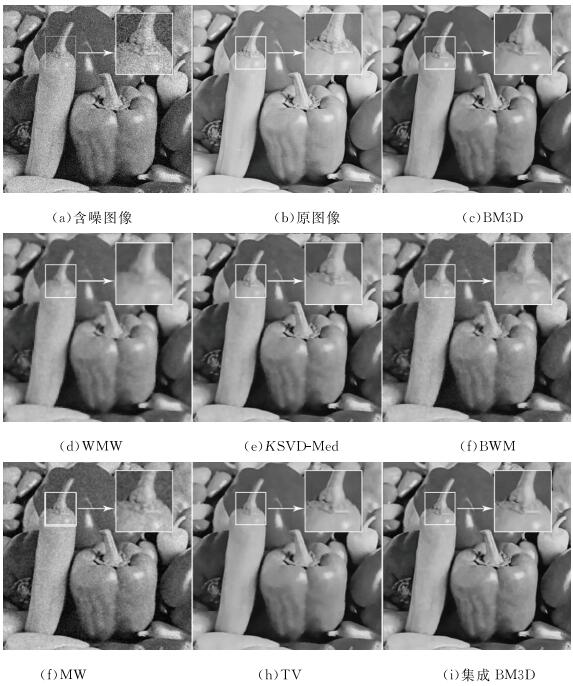
图 4为含有0.01/0.000 5型噪声的Peppers去噪结果。结果表明TV法、WMW法图像模糊严重;BWM和MW法虽有一定的细节保留,但有噪声残留;而KSVD-Med法则兼顾了去噪和纹理细节的保留,但相比之下,BM3D和集成BM3D具有更大的优势。从图 4白框“椒梗”区域的去噪结果来看,各方法在去噪和细节保留上的差异,BM3D、TV和集成BM3D 3种方法不仅噪声去除彻底,而且对纹理和边缘的保留较为完好,优于其他各种方法,突出了基于BM3D的去噪方法的优势。
|
| 图 4 使用不同方法的Peppers图像去噪结果 Fig. 4 Denoising Result of Noisy Peppers Image Using Different Methods |
在定量分析方面,表 1为两种含噪图像去噪质量评价指标表,可以看出,集成BM3D法PSNR和MSE在所有方法中表现最佳;BM3D法、KSVD-Med法和TV法也均有较高的PSNR和较低的MSE,但存在细节的丢失,尤其TV法在噪声含量较大时图像模糊较严重,导致去噪质量不如集成BM3D方法;而WMW、BWM和MW 3种方法PSNR相对较低、MSE较大,主要是由于过度去噪造成图像模糊或噪声去除不充分,结果与真实图像信号相差较大。
| 方法 | Lena图像 | Peppers图像 | |||||||||
| 0.01/0.000 5 | 0.05/0.001 | 0.01/0.000 5 | 0.05/0.001 | ||||||||
| PSNR | MSE | PSNR | MSE | PSNR | MSE | PSNR | MSE | ||||
| BM3D | 35.66 | 17.67 | 32.57 | 36.02 | 35.07 | 20.25 | 31.61 | 44.89 | |||
| WMW | 33.16 | 31.42 | 31.28 | 48.41 | 33.22 | 30.99 | 30.83 | 53.71 | |||
| K-SVD | 34.99 | 20.61 | 31.54 | 45.59 | 34.53 | 22.90 | 31.14 | 50.02 | |||
| KSVD-Med | 34.93 | 20.89 | 31.55 | 45.55 | 34.50 | 23.08 | 31.14 | 50.03 | |||
| BWM | 33.00 | 32.59 | 30.49 | 58.03 | 33.03 | 32.39 | 30.13 | 63.13 | |||
| MW | 32.94 | 33.03 | 29.70 | 69.65 | 32.96 | 32.91 | 29.70 | 69.61 | |||
| TV | 34.50 | 23.10 | 31.44 | 46.68 | 34.42 | 23.50 | 31.36 | 47.57 | |||
| 集成BM3D | 35.71 | 17.45 | 33.09 | 31.90 | 35.43 | 18.64 | 33.00 | 32.58 | |||
为验证算法对遥感影像去噪的适用性,选用一块质量较好的QuickBird(QB)样例影像(见图 5)验证集成BM3D法的去噪效果。为充分说明方法的有效性,检验该方法在不同混合噪声类型下的鲁棒性,分别加入4种遥感影像中常见的高斯、脉冲混合噪声类型(0.01/0.000 5、0.02/0.001、0.05/0.001、0.1/0.01),并进行去噪实验。

|
| 图 5 原始的无噪QB样例影像 Fig. 5 Clear QuickBird Sample Image |
集成BM3D去除不同类型混合噪声的结果如图 6所示,与其他多种方法去噪质量评价因子的对比结果见表 2。由图 6可以看出,集成BM3D法可有效去除不同类型混合噪声,在噪声相对较少时,去噪后的影像视觉效果非常好,而当噪声含量较多时,如图 4(h)所示,虽然仍不可避免出现少许的图像模糊,但大多纹理、边缘、梯度变换等细节均得到保留。尤其是梯度变化信息的保留使去噪后的影像仍符合地理要素的空间自相关性,对地形的遥感定量研究具有极大的意义。

|
| 图 6 集成BM3D法对不同混合噪声去除结果 Fig. 6 Result of Denoising of Different Mixture Noise Contaminated Image by Assemble BM3D |
| 方法 | 0.01/0.000 5 | 0.02/0.001 | 0.05/0.001 | 0.1/0.01 | |||||||
| PSNR | MSE | PSNR | MSE | PSNR | MSE | PSNR | MSE | ||||
| BM3D | 31.97 | 41.28 | 30.91 | 52.77 | 29.67 | 70.24 | 28.84 | 84.90 | |||
| WMW | 29.66 | 70.33 | 29.47 | 73.38 | 29.06 | 80.91 | 28.52 | 91.37 | |||
| KSVD-Med | 31.50 | 46.07 | 30.41 | 59.13 | 29.20 | 78.16 | 28.51 | 91.72 | |||
| BWM | 29.79 | 68.17 | 29.57 | 71.72 | 28.96 | 82.68 | 28.30 | 96.21 | |||
| MW | 31.01 | 51.48 | 30.34 | 60.18 | 29.37 | 75.10 | 28.75 | 86.79 | |||
| TV | 30.86 | 53.31 | 30.08 | 63.87 | 29.04 | 81.03 | 28.30 | 96.13 | |||
| 集成BM3D | 32.05 | 40.58 | 31.11 | 50.41 | 30.07 | 63.97 | 29.45 | 73.77 | |||
表 2说明不同方法对不同噪声类型的去噪影像质量评价因子存在较大差异,但本文提出的集成BM3D法最优。其他方法则在不同程度上弱于本文算法。同时从表 2中可以看出,随着噪声含量的增加,本文算法对比BM3D法优势愈加显著,在一定程度上反映了单独的BM3D去噪在噪声含量较大时图像模糊加重,而本文提出的集成策略则恰好将丢失的细节信号保留下来。
研究表明,集成BM3D法优于其他方法,不仅能高效去噪,而且可以保留较多的图像细节信息。而更多实验表明,当脉冲噪声含量较多而高斯噪声相对较少时,BM3D去噪会遗留大量脉冲噪声。相比之下,集成BM3D则适用于各种高斯与脉冲噪声混合情况,比BM3D法保留更多边缘、纹理等细节信息,尤其是噪声含量较多时,集成BM3D法优势愈加明显。
4 结语遥感影像噪声会对影像质量产生较大影响,因此去噪处理是遥感应用性研究尤其是定量遥感研究必不可少的一环。本文在分析了图像去噪研究进展的基础上,针对BM3D稀疏去噪方法对含有脉冲噪声的混合噪声去除所存在的缺陷,提出了一种集成BM3D去噪策略,发展了改进的噪声估算方法M-Liu法用于噪声量估算,并验证了该集成方法的去噪特性。
研究表明,提出的集成BM3D法具有较好的去噪特性,能兼顾影像噪声去除和细节信号的保留,可在一定程度上弥补BM3D低噪声含量去噪时细节丢失和高噪声含量去噪时脉冲噪声遗留的缺陷,与同类方法相比,优势较为明显,对于遥感影像后期应用性研究具有一定的意义,也可为图像去噪提供新的方法借鉴。
但由于该算法以先验噪声含量为算法输入参数,实际的影像去噪中需要进行先验噪声估算,虽然改进的M-Liu法能在一定程度上提高噪声含量估算精度,但仍非真实值,影响去噪效果,因此先验噪声估算方面仍具有改进的空间,需开展进一步的研究。
| [1] |
Xia Liangzheng, Li Jiuxian. Digital Image Proces-sing[M]. Nanjing: Southeast University Press, 2011. (夏良正, 李久贤. 数字图像处理[M]. 南京: 东南大学出版社, 2011. )
|
| [2] |
Liu Xiaoli, Ren Liqiu, Li Wei, et al. Threshold Optimized Wavelet for Remotely Sensed Image Denoising[J]. Remote Sensing Information, 2016, 31(2): 109-113. (刘晓莉, 任丽秋, 李伟, 等. 阈值优化的遥感影像小波去噪[J]. 遥感信息, 2016, 31(2): 109-113. DOI:10.3969/j.issn.1000-3177.2016.02.020 ) |
| [3] |
Li Jianping. Wavelet Analysis and Signal Processing[M]. Chongqing: Chongqing Press, 1997. (李建平. 小波分析与信号处理[M]. 重庆: 重庆出版社, 1997. )
|
| [4] |
Dabov K, Foi A, Katkovnik V, et al. Image Denoising by Sparse 3-D Transform-domain Collaborative Filtering[J]. IEEE Transactions on Image Processing, 2007, 16(8): 2080-2095. DOI:10.1109/TIP.2007.901238 |
| [5] |
He Kun, Ju Shenggen, Lin Tao, et al. Image Denoising on TV Numerical Computation[J]. Journal of University Electronic Science and Technology of China, 2013, 42(3): 459-463. (何坤, 琚生根, 林涛, 等. TV数值计算的图像去噪[J]. 电子科技大学学报, 2013, 42(3): 459-463. DOI:10.3969/j.issn.1001-0548.2013.03.027 ) |
| [6] |
Laine A F. Wavelet Applications in Signal and Ima-ge Processing[M]. Washington D C: SPIE-the International Society for Optical Engineering, 2000.
|
| [7] |
Xia Qin, Xing Shuai, Ma Dongyang, et al. An Improved K-SVD Based Denoising Method for Remote Sensing Satellite Images[J]. Journal of Remote Sensing, 2016, 20(3): 441-449. (夏琴, 邢帅, 马东洋, 等. 遥感卫星影像K-SVD稀疏表示去噪[J]. 遥感学报, 2016, 20(3): 441-449. ) |
| [8] |
Muresan D D, Parks T W. Adaptive Principal Components and Image Denoising[C]. International Conference on Image Processing, IEEE, Spain, 2003 http://www.researchgate.net/publication/4044605_adaptive_principal_components_and_image_denoising?ev=sim_pub
|
| [9] |
Elad M, Aharon M. Image Denoising Via Sparse and Redundant Representations over Learned Dictionaries[J]. IEEE Transactions on Image Proces-sing, 2006, 15(12): 3736-3745. DOI:10.1109/TIP.2006.881969 |
| [10] |
Yuan Wencheng, Yang Dexing, Chen Chao. A Synthetic Filtering Method for Restoration of Images Contaminated by Mixed Noise[J]. Microprocessors, 2007, 28(4): 78-80. (袁文成, 杨德兴, 陈超. 图像混合噪声的一种组合滤波消除方法[J]. 微处理机, 2007, 28(4): 78-80. DOI:10.3969/j.issn.1002-2279.2007.04.027 ) |
| [11] |
Dong H, Wang F. Image-Denoising Based on Bior Wavelet Transform and Median Filter[C]. Photonics and Optoelectronics (SOPO), Shanghai, China, 2012 http://www.researchgate.net/publication/261498749_Image-Denoising_Based_on_Bior_Wavelet_Transform_and_Median_Filter
|
| [12] |
Zhu Jianjun, Zhou Jinghong, Zhou Cui, et al. A New Combination Filtering Method to Remove Mixed Noise of Remote Sensing Images[J]. Geomatics and Information Science of Wuhan University, 2017, 42(3): 348-354. (朱建军, 周靖鸿, 周璀, 等. 一种新的去除遥感影像混合噪声组合滤波方法[J]. 武汉大学学报·信息科学版, 2017, 42(3): 348-354. ) |
| [13] |
Donoho D L. De-noising by Soft-Thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 613-627. DOI:10.1109/18.382009 |
| [14] |
Donoho D L, Johnstone I M. Adapting to Unknown Smoothness via Wavelet Shrinkage[J]. Journal of the American Statistical Association, 1995, 90(432): 1200-1224. DOI:10.1080/01621459.1995.10476626 |
| [15] |
Lim J S. Two-dimensional Signal and Image Processing[M]. Upper Saddle River: Prentice Hall, 1990.
|
| [16] |
Aja-Fernández S, Alberola-López C. Automatic Noise Estimation in Images Using Local Statistics. Additive and Multiplicative Cases[J]. Image and Vision Computing, 2009, 27(6): 756-770. DOI:10.1016/j.imavis.2008.08.002 |
| [17] |
Pyatykh S, Hesser J, Zheng L. Image Noise Level Estimation by Principal Component Analysis[J]. IEEE Transactions on Image Processing, 2013, 22(2): 687. DOI:10.1109/TIP.2012.2221728 |
| [18] |
Liu X, Tanaka M, Okutomi M. Noise Level Estimation Using Weak Textured Patches of a Single Noisy Image[C]. Image Processing (ICIP), 19th IEEE International Conference on, IEEE, Orlando, USA, 2012 http://www.researchgate.net/publication/261387053_Noise_level_estimation_using_weak_textured_patches_of_a_single_noisy_image
|
| [19] |
Schneider C, Gürenci J. Mathematical Problems in Image Processing:Partial Differential Equations and the Calculus of Variations[M]. New York: Springer, 2009.
|
| [20] |
Ichigaya A, Nishida Y, Nakasu E. Nonreference Method for Estimating PSNR of MPEG-2 Coded Video by Using DCT Coefficients and Picture Energy[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2008, 18(6): 817-826. |
| [21] |
Salman A G, Kanigoro B, Rojali, et al. Application Hiding Messages in JPEG Images with the Method of Bit-Plane Complexity Segmentation on Android-Based Mobile Devices[C]. Elsevier Ltd, Jakarta D C, 2012
|
 2019, Vol. 44
2019, Vol. 44



