
文章信息
- 吴富梅, 魏子卿
- WU Fumei, WEI Ziqing
- 利用GNSS和EGM2008模型进行跨海高程传递
- Height Transfer from Land to Island Based on GNSS and EGM2008 Model
- 武汉大学学报·信息科学版, 2016, 41(5): 698-703
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 698-703
- http://dx.doi.org/10.13203/j.whugis20140392
-
文章历史
- 收稿日期: 2015-04-27

2. 西安测绘研究所, 陕西西安, 710054
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
跨海高程传递是开展海洋及岛礁精确测绘的关键技术之一。跨海高程传递的方法有多种,如静力水准法、动力水准法以及精密水准测量和三角高程测量[1]。静力水准法、动力水准法因其价格昂贵且周期较长,现在一般不予采用,精密水准测量的视距很短,在跨海高程传递中应用受限。三角高程测量是一种常用的跨海高程传递方法,在许多工程中得到比较广泛的应用,但这种方法耗费时间和财力,而且精度受到一定限制。
随着空间大地测量技术的发展,GNSS的出现为大地测量带来突破性的变革。利用GNSS定位获得的坐标精度在水平方向可达毫米级,在垂直方向可达厘米级。但GNSS获得的大地高的基准面是参考椭球面,而不是平均海水面,因此出现了GNSS水准。所谓GNSS水准就是在获得参考椭球面与大地水准面(或似大地水准面)差距的前提下,以GNSS测量来代替水准测量,因此精确确定大地水准面(或似大地水准面)是GNSS水准测量的先决条件[2]。我国海域高精度的大地水准面模型尚未建立,目前利用GNSS水准实现跨海高程传递还有一定困难。
本文提出了一种利用GNSS和EGM2008模型进行跨海高程传递的方法。其实现步骤为:选定一个高程已知点,利用GNSS测定已知点和待求点的三维大地坐标,利用地球引力位模型获取点位的重力位,最后经过计算处理得到待求点的正高或正常高。这种方法简单、快捷,不需要水准测量,也不需要高精度的大地水准面。
1 基本原理
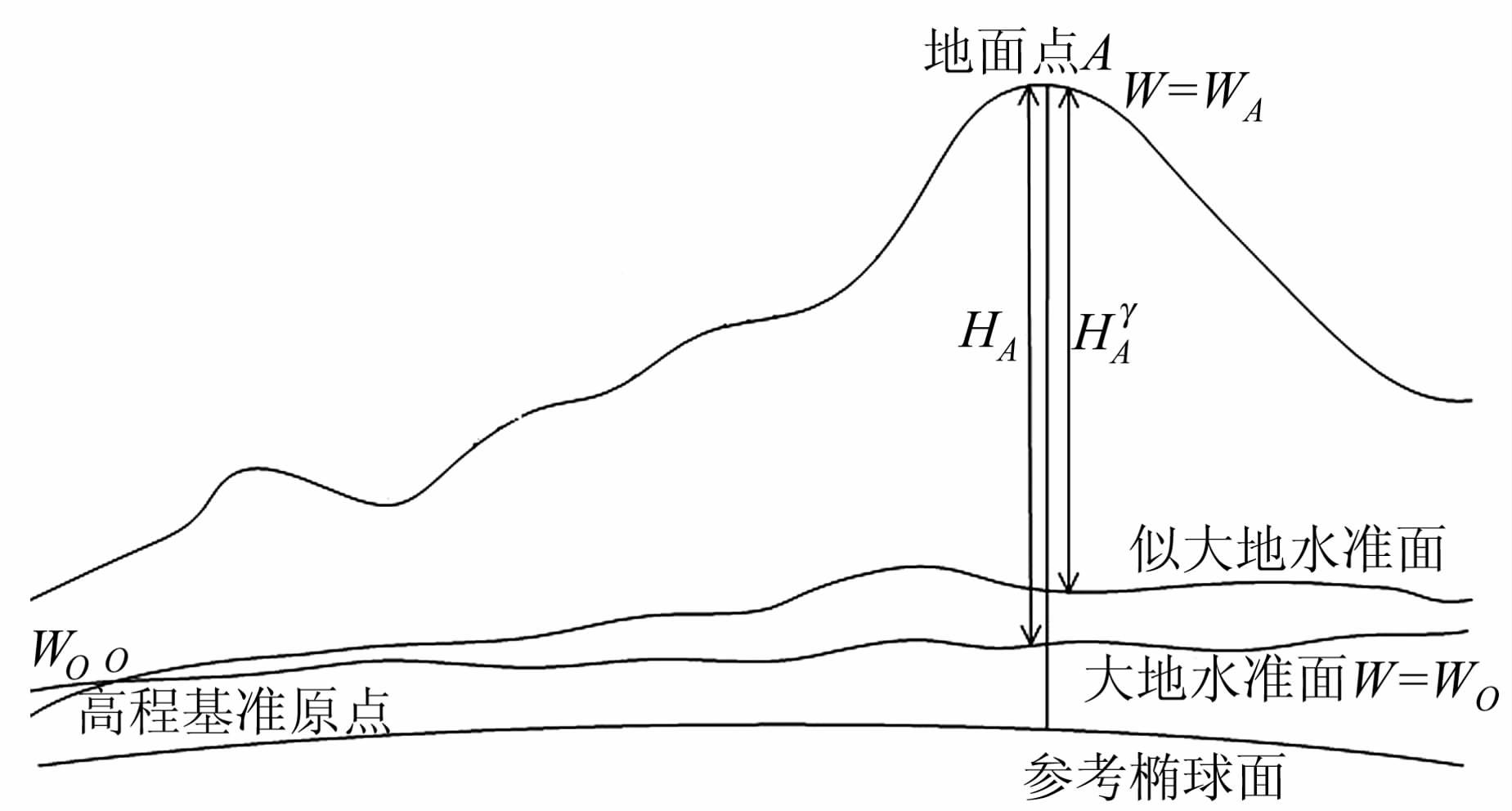
假定已知高程基准点的重力位是WO,通过水准测量和重力测量或者其他方式可以获得待求点相对高程基准点的重力位差WO-WA(见图 1)。对于正常高系统,待求点的高程可以表示为:
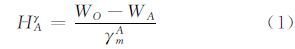
式中,HAγ为A点的正常高;WA为A点的重力位;γmA为A点沿铅垂线至似大地水准面之间的平均正常重力。
对于正高系统,A点的高程为:
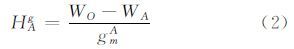
式中,HAg为A点的正高;gmA为A点沿铅垂线至大地水准面之间的平均重力。
|
| 图 1 重力位与高程系统 Fig. 1 Gravity Potential and Height System |
根据IERS标准[3],大地水准面的重力位WO=62 636 856.0 m2s-2。事实上,由于受局部因素影响,很多国家定义高程基准的验潮站的重力位WO并不等于这一数值,如我国青岛验潮站的WO=62 636 852.85 m2s-2[4]、波罗的海的WO=62 636 855.507 m2s-2[5, 6]。对于用户,高程基准点的WO往往是未知的,这种情况下,引入高程已知点B作为参考,对于点B同样可以得到类似式(1)和式(2)的高程表达式。消去A、B点高程表达式中的WO,则待求点A的正常高和正高为:
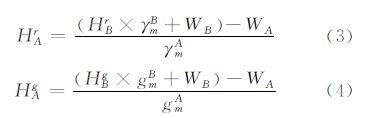
在上面确定高程的公式中,有两种量是需要确定的。一是A点和B点的重力位WA、WB,二是A点和B点的平均正常重力γmA、γmB或平均重力gmA、gmB。
A点或B点的重力位可以用最新引力位模型计算:
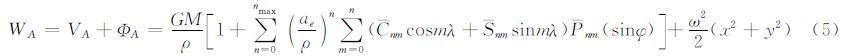
式中,VA为A点的引力位;ΦA为A点的离心力位;GM为地心引力常数;ρ为地心向径,ρ=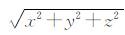 ;ae为参考椭球长半轴;Cnm、Snm为完全正常化的n阶m次地球引力位系数;φ、λ为地心纬度和经度,
;ae为参考椭球长半轴;Cnm、Snm为完全正常化的n阶m次地球引力位系数;φ、λ为地心纬度和经度,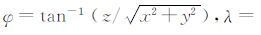 ,
,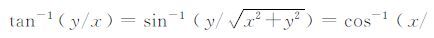
 为完全正常化的n阶m次缔合勒让德函数;ω为地球自转角速度;(x,y,z)为地心直角坐标;nmax为引力位模型阶数。
为完全正常化的n阶m次缔合勒让德函数;ω为地球自转角速度;(x,y,z)为地心直角坐标;nmax为引力位模型阶数。
对于正常高系统,A点或B点至似大地水准面的平均正常重力有[7]:
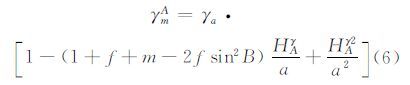
式中,f表示椭球扁率;γa表示点A在椭球面上的投影点的正常重力;HAγ表示A点的正常高;a表示椭球长半轴;B表示A点的大地纬度;m=ω2aγa。
对于正高系统,A点至大地水准面的平均重力有[8]:
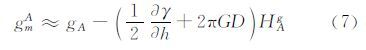
式中,gA表示A点的重力;γh=-0.308 6×10-5s-2为正常重力梯度;2πGD是与该地区地壳密度相关的量,一般可取成0.111 6×10-5s-2;HAg为A点的正高,单位为m。
这样,A点至大地水准面的平均重力为:
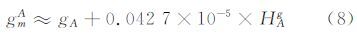
对于B点有类似的公式。
A点的重力可通过引力位模型获得:
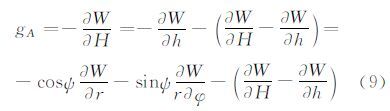
其中,
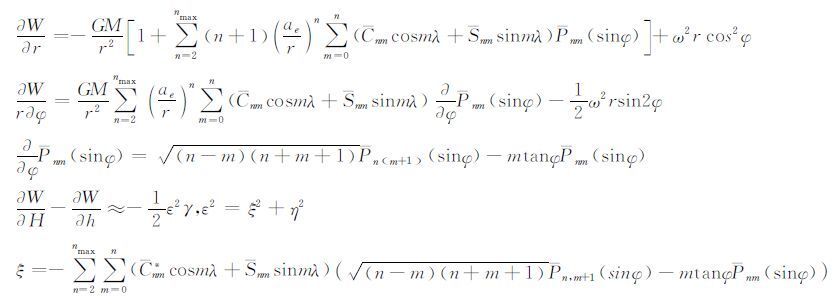
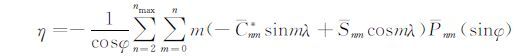
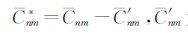 为参考椭球的完全正常化位系数(当m为奇数时,C′nm=0)。
为参考椭球的完全正常化位系数(当m为奇数时,C′nm=0)。
相比于正常高,正高的计算,除了引力位模型误差,还包含平均重力计算引入的误差。下文以正高为例,对计算得到的高程进行误差分析,由式(4)有:
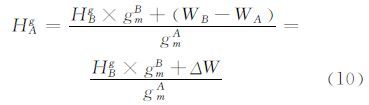
其中,有误差影响的项是gmA、gmB、ΔW和HBg,将上式进行微分,有:
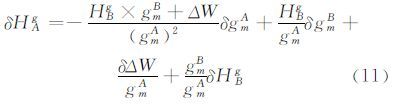
首先分析δgmA的大小。采用一组美国实测重力数据评估式(9)计算的重力精度,共计1 000点。经统计,其误差均值-1.280 mGal,均方误差3.681 mGal。另外,对正高1 000 m的点,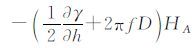 的影响不超过9 mGal,因此利用模型获得的平均重力误差在10 mGal量级。
的影响不超过9 mGal,因此利用模型获得的平均重力误差在10 mGal量级。
令gmA≈10 m/s2,gmB≈10 m/s2,δgmA≈10 mGal,ΔW≈1 000 m2/s2(A、B两点高差约为100 m),则:
1) 当HBg≈100 m时,
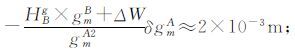
2) 当HBg≈1 000 m时,
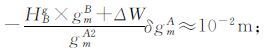
3) 当HBg≈5 000 m时,
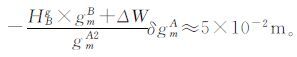
因此,在理想情况下,在海拔高低于5 000 m的区域,A、B两点高差不超过100 m,该项误差小于5 cm。
同样地,按照上文的假定,右端第二项误差小于5 cm。
3.2 右端第三项误差令gmA≈10 m/s2,则δΔW=δWB-δWA,mΔW2=mWB2+mWA2-2CovWBWA。mWB2是B点的引力位误差,mWA2是A点的引力位误差,CovWBWA是WB与WA的协方差。
引力位误差包括由GNSS三维位置误差引起的误差和引力位模型本身引起的误差。
在三维位置误差中,唯有大地高方向误差才产生重要影响,而且可以认为以1∶1的比例传播至计算的高程中[2]。因此,按照当前GNSS观测水平,大地高方向可以达到cm级,由三维位置误差引起的误差在cm级。
引力位模型误差包括过失误差和截断误差,以B点为例,过失误差和截断误差分别为:
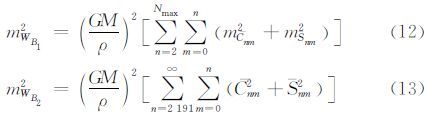
式中,mCnm2、mCnm2是引力位模型系数误差;Cnm、Cnm≈±10-5/n2[2]。EGM2008模型计算得到的mWB12=0.700 m4/s4,mWB22=0.085 m4/s4。
认为A、B两点引力位模型误差相等,则引力位差的模型误差为:
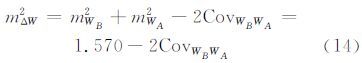
当CovWBWA=0.0时,即当A、B两点的重力位误差独立时,δΔW/gmA≈0.125 m;当CovWBWA≠0.0时,即当A、B两点的重力位误差相关时,δΔW/gmA<0.125 m。理论上,引力场位模型引起的误差具有相关性,待求点与已知点距离越近,相关性越大,距离越远,相关性越小。
此项误差与已知点高程误差相关,几乎以1∶1比例传播至未知点高程,但此项误差非本文算法能减小的,因此在此不考虑。
综合前三项误差,得到高程总误差约为0.150 m(假定大地高误差5 cm)。值得注意的是,在误差分析时考虑了已知点的重力位误差。实际上,高程传递时,一般仅考虑两点间的相对误差,再顾及两点间的误差相关性,所以在中等距离范围内高程传递误差应小于0.150 m。
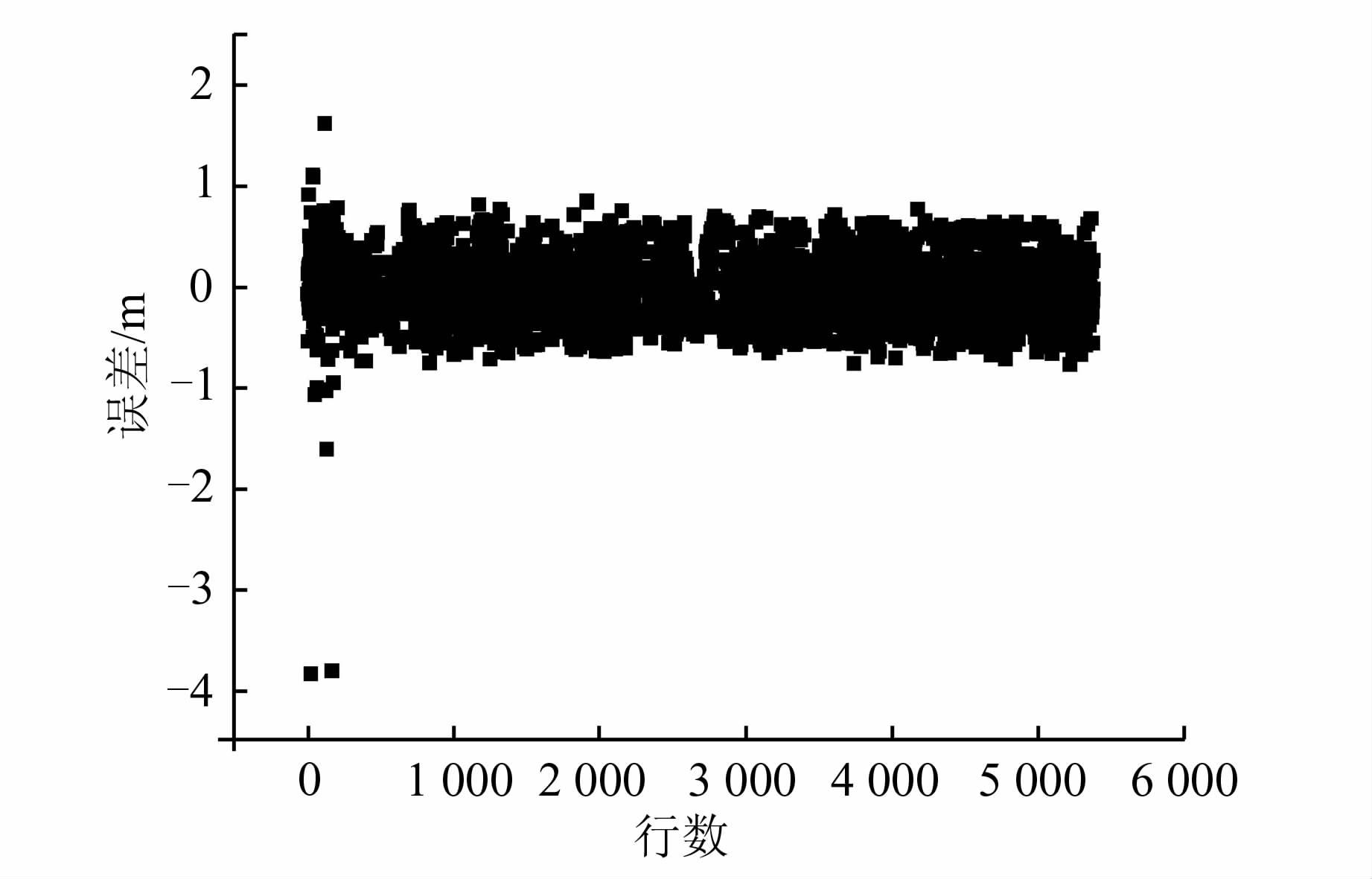
4 计算与比较 4.1 正高计算利用一组美国实测GNSS/水准数据评估式(4)获得的正高精度,共计5 378个点,以“0123104”作为已知点(纬度39.203 ° ,经度275.449 °,大地高241.033 m)。图 2给出了GNSS/水准数据的点位分布,图 3给出了计算的正高与实测值的差值。
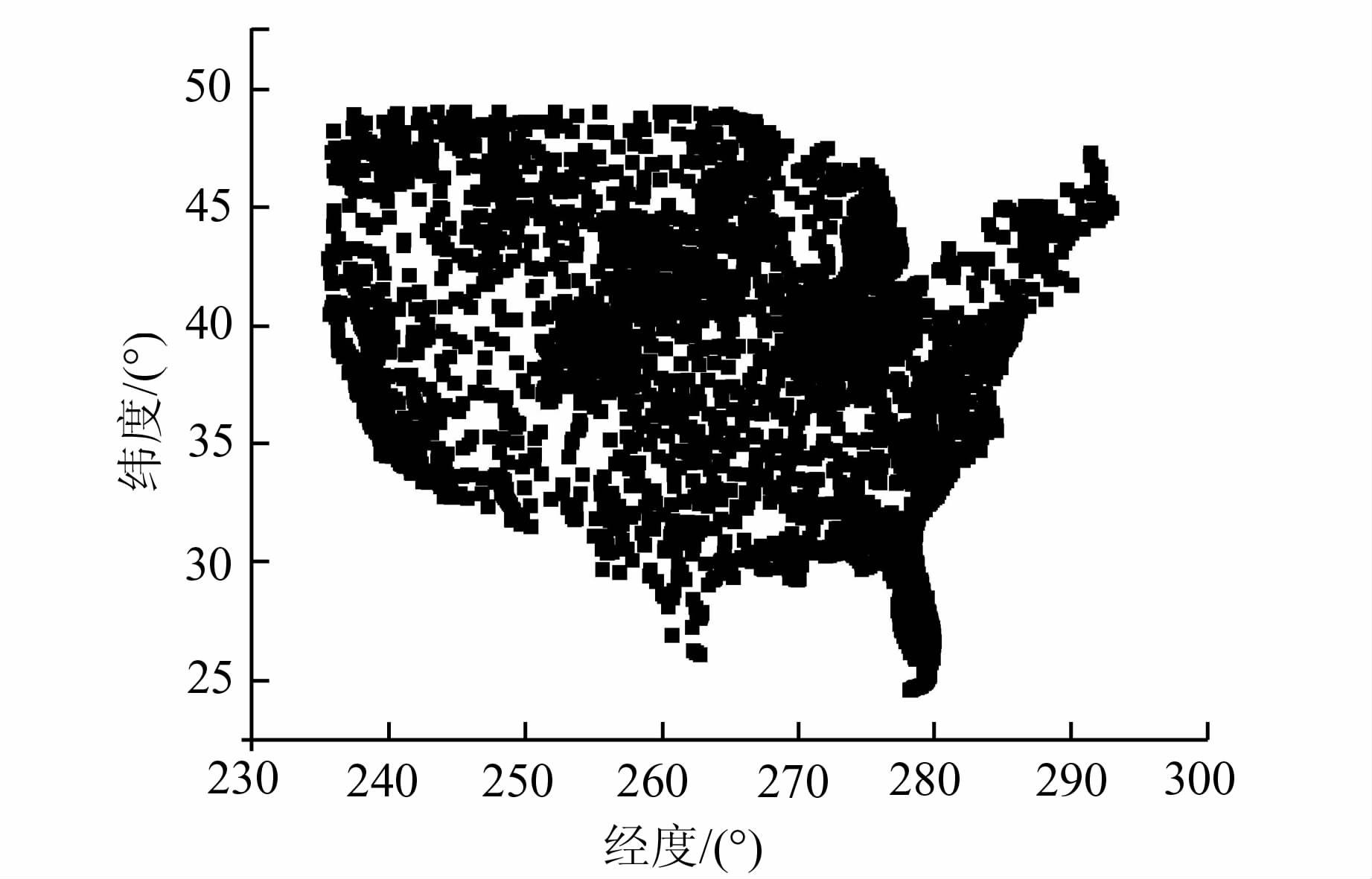
|
| 图 2 点位分布 Fig. 2 Points Distribution |
|
| 图 3 计算的正常高与实测值的差值 Fig. 3 Difference Between Calculated Value and Actual Value |
经统计,模型计算的正高精度为0.295 m。由于大部分待求点与已知点距离较远,且高程大于1 000 m,因此计算获得的正高精度较低。
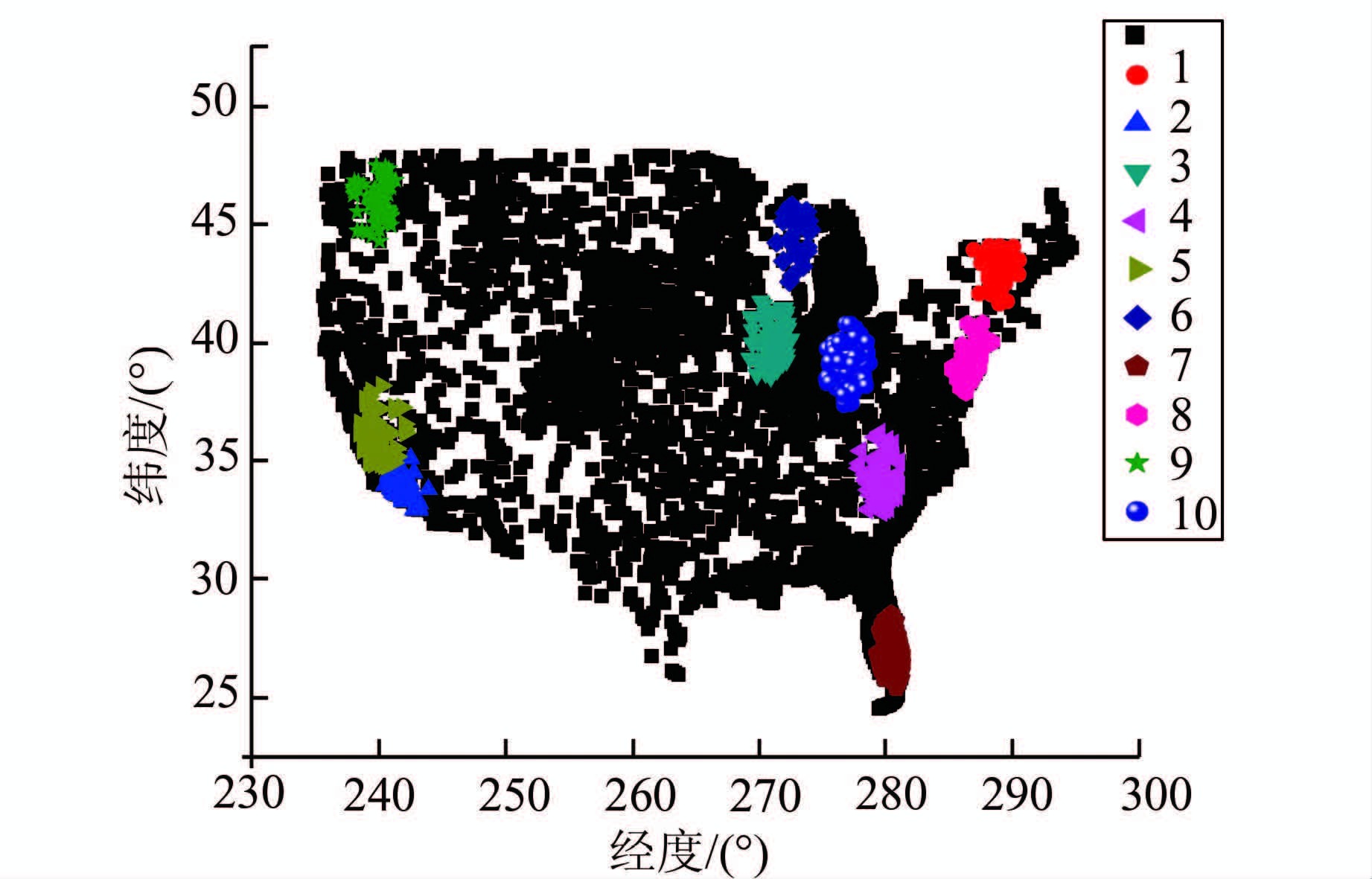
从图 2中选择10个地势较平坦的区域(见图 4),每个区域选择中心点作为已知点,计算其周围500 km范围内每个点的正高。按不同距离范围统计高程计算值与实测值的差值,如表 1所示。
|
| 图 4 10个分区图 Fig. 4 10 Subnets |
| 点数 | 平均高度/m | 平均距离/km | 精度/m | |
| 10~30 km | 92 | 149.67 | 21.2 | 0.056 |
| 40~60 km | 226 | 143.71 | 51.7 | 0.063 |
| 90~110 km | 102 | 143.21 | 99.2 | 0.072 |
| 190~210 km | 202 | 153.87 | 199.6 | 0.085 |
| 290~310 km | 170 | 265.86 | 300.6 | 0.143 |
| 390~410 km | 188 | 243.87 | 399.5 | 0.116 |
| 490~500 km | 118 | 176.22 | 494.5 | 0.116 |
由表 1可知,计算的正高与已知点的距离相关,一般地,距离越近,精度越高,距离越远,精度越低;当计算点距离已知点200 km以内,计算的正高精度优于10 cm。
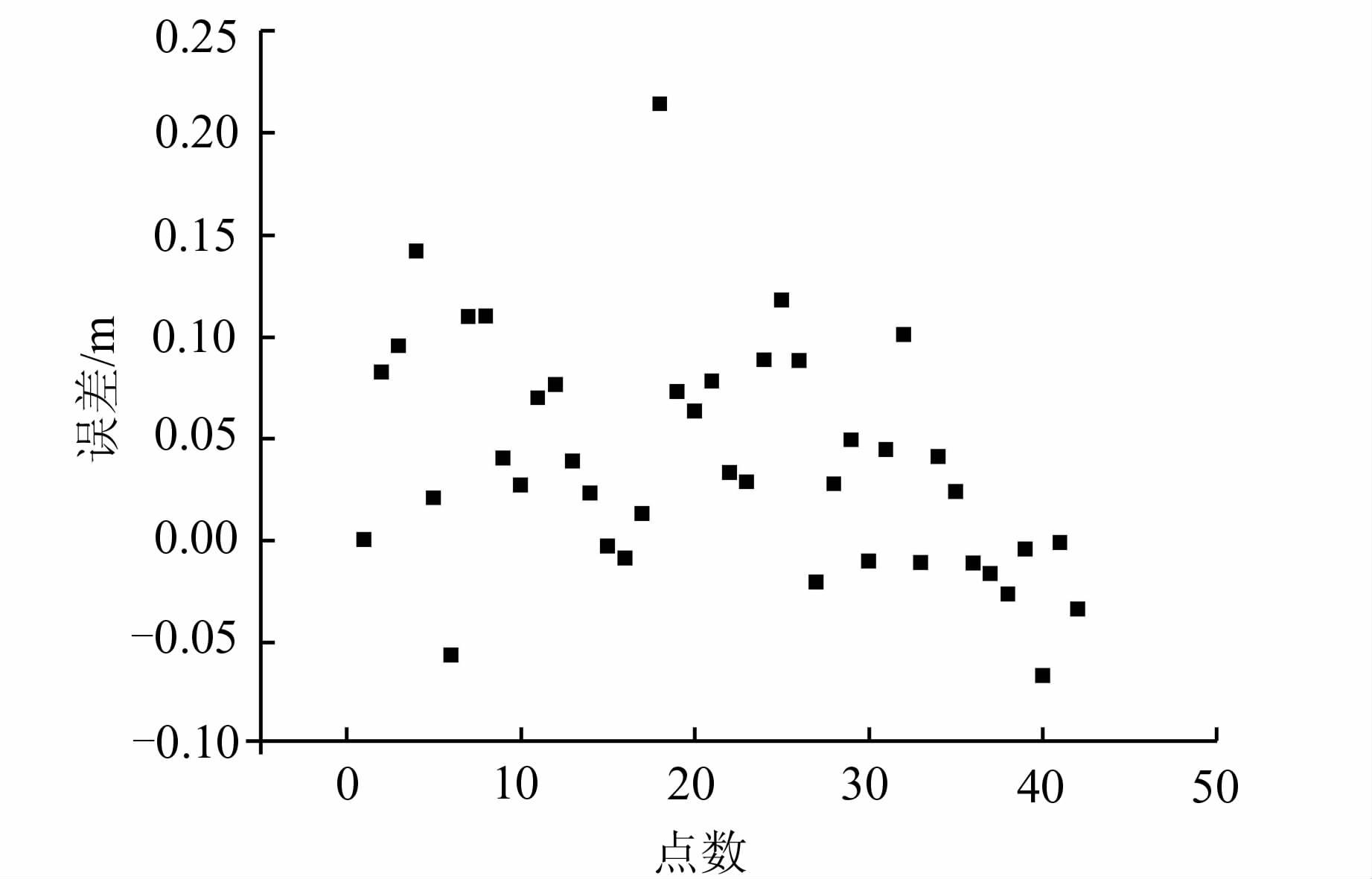
4.2 正常高计算利用我国西北区域实测的43个GNSS/水准点进行验证,点分布在100 km内,以“X01B”作为已知点(纬度41.270 ° ,经度100.338 °,大地高1 000.728 m)。图 5给出了计算的正常高与实测值的差值。
|
| 图 5 计算的正常高与实测值的差值 Fig. 5 Difference Between Calculated Value and Actual Value |
经统计,模型计算的正常高精度0.068 m。
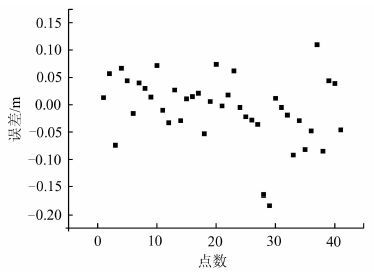
利用我国沿海的41个岛礁点进行验证,每个岛礁点对应陆地一个已知点,岛礁点正常高通过三角高程测量获得(精度为5 cm),岛礁点距离相应已知点的平均距离是6.982 km。图 6给出了计算的正常高与三角高程计算值的差值,其中在海南附近岛礁有两点的计算值误差较大,达到0.16 m和0.18 m,其原因尚不明确。
经统计,模型计算的正常高精度0.060 m,与三角高程测量精度相当。
|
| 图 6 计算的正常高与三角高程计算值的差值 Fig. 6 Difference Between Calculated Value and Actual Value |
相比于传统跨海高程传递方法,利用GNSS和EGM2008模型能够实现较高精度的跨海高程传递,简单、快捷且节约成本。这种方法计算获得高程精度与该点高程和重力场模型计算的重力位精度相关。高程越高,该方法计算的海拔高精度越低;待求点距离已知点越远,计算的高程精度越低。在距离已知点200 km范围内,高程精度优于10 cm,距离已知点10 km范围内,高程精度达到6 cm,达到与三角高程测量相当的精度。
需要说明的是,这种高程获取方法不仅适用于跨海岛礁的高程传递,也适用于陆地中短距离的高程传递。
致谢:感谢有关部门为本文计算提供岛礁测量数据、GNSS水准数据和便利条件。
| [1] | Li Jiancheng, Jiang Weiping. Height Datum Trans-ference within Long Distance Across Sea[J]. Geomatics and Information Science of Wuhan University, 2001,26(6):514-517(李建成, 姜卫平. 长距离跨海高程基准传递方法的研究[J].武汉大学学报·信息科学版,2001,26(6):514-517) |
| [2] | Wei Ziqing. GPS Gravity-Potential Leveling[J].Journal of Geodesy and Geodynamics, 2007,27(4):1-7(魏子卿.GNSS重力位水准[J]. 大地测量与地球动力学,2007,27(4):1-7) |
| [3] | McCarthy D D, Petit G. IERS Conventions (2003)[R]. IERS Technical Note No.32,Frankfurt, Germany, 2004 |
| [4] | Zhai Zhehe, Wei Ziqing, Wu Fumei, et al. Computation of Vertical Deviation of Chinese Height Datum from Geoid by Using EGM2008 Model[J]. Journal of Geodesy and Geodynamics, 2011,31(4):116-118(翟振和, 魏子卿, 吴富梅,等.利用EGM08位模型计算我国高程基准与大地水准面间的垂直偏差[J].大地测量与地球动力学,2011,31(4):116-118) |
| [5] | Ardalan A, Grafarend E. A First Test for W0 the Time Variation of W0 Based on Three GNSS Campaigns of the Baltic Sea Level Project[M]. Berlin:Springer, 2003 |
| [6] | Pavlis N K,Holmes S A,Kenyon S C, et al. An Earth Gravitational Model to Degree 2160:EGM2008[C]. The 2008 General Assembly of the European Geosciences Union, Vienna, Austria, 2008 |
| [7] | Heiskanen W A, Moritz H. Physical Geodesy[M]. London, UK:Freeman W H and Company, 1967 |
| [8] | Hofmann-Wellenhof B, Moritz H. Physical Geodesy[M]. New York:Springer, 2006 |
 2016, Vol. 41
2016, Vol. 41



