文章信息
- 匡翠林, 张晋升, 卢辰龙, 易重海
- KUANG Cuilin, ZHANG Jinsheng, LU Chenlong, YI Zhonghai
- GPS单双频混合方法在地表形变监测中的应用
- Single-and Dual-Frequency Mixed Mode GPS Network for Ground Deformation Monitoring
- 武汉大学学报·信息科学版, 2016, 41(5): 692-697
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 692-697
- http://dx.doi.org/10.13203/j.whugis20140051
-
文章历史
- 收稿日期: 2014-09-13

2. 湖南省精密工程测量与形变灾害监测重点实验室, 湖南长沙, 410083
2. Key Lab of Precise Engineering Surveying & Deformation Disaster Monitoring of Hunan Province, Changsha 410083, China
随着城市用水的增加,人们大量开采地下水,同时由于地铁、地下商场等地下建筑物的修建,很多地区的地表发生了严重的形变,因此,有必要建立连续监测网监测地表形变。GPS使用方便、误差积累较小,且能实时获取地表三维绝对形变信息,因而在边坡、大坝以及地表沉降等变形监测中应用广泛[1, 2, 3]。利用GPS进行地表形变监测时,通常采用相对定位方法,影响其结果精度的主要因素是对流层延迟和电离层延迟。对流层延迟通常采用模型改正,改正后的残余误差采用参数估计方法;电离层由于其活跃性与不确定性,一般采用双频消电离层组合的方法消除。
较早的GPS连续观测网络是1988年在日本建立的,其主要用于研究地震预报。其后,大量的连续性GPS观测网络被建立起来用于桥梁、建筑物以及火山等形变监测[4, 5, 6]。为了获得高精度的结果,这些监测网一般采用双频大地型GPS接收机,从而导致工程应用成本很高。为了降低变形监测的费用,可以考虑使用单频GPS接收机,但是其不能通过双频消电离层组合直接消除电离层延迟一阶项影响[6],从而导致精度下降,因此,单频GPS一般用于小范围的变形监测。但是,在电离层活跃年份如2013年,或是在低纬度地区,即使基线较短,电离层误差空间相似性并不理想,这样势必影响单频GPS定位精度,且导致模糊度收敛时间延长[7, 8]。因此,本文采用GPS单双频混合模式,即在变形监测外围布设双频GPS接收机,在变形监测区域内部布设单频GPS接收机,通过双频GPS观测数据建立大气延迟误差的改正信息,将其用于改正监测点的单频数据,从而实现了在降低变形监测成本的同时又保证了监测精度[9, 10]。
1 区域大气延迟误差残余量改正
GPS大气延迟误差主要包括电离层延迟和对流层延迟两部分,其中电离层又因其活跃性和不确定性而常给基线解算引入较大误差。在短基线处理中通常认为通过双差处理后的残余大气延迟误差已足够小,不会对基线解算结果造成影响。但是,在电离层活跃年份或是低纬度区域,即使是短基线两端的站点其电离层误差也不能通过双差算法很好地消除。
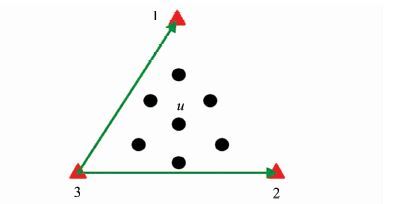
采用双频接收机可以通过消电离层组合的方式消除电离层一阶项影响,但双频GPS费用较高,而单频GPS虽价格较低,却又无法通过观测值组合直接消除电离层误差。因此综合考虑单双频GPS的优缺点,可以在变形监测网中的基准站上安装双频接收机,监测站上安装单频接收机,采用双频GPS观测数据生成区域大气延迟误差改正项,用于改正监测站点的单频观测数据[11, 12]。图 1所示为理想(即所有单频站点全部位于双频站点区域内部)的站点分布图,其中三角形表示双频基准站点,圆点表示单频监测站点。
|
| 图 1 理想情况下单双频混合布设示意图 Fig. 1 Ideal Network Configuration of a Mixed-Mode GPS Deformtion monitoring Network |
已知双差相位观测方程为:
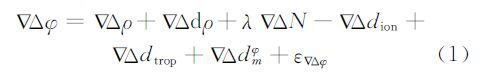
式中,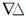 表示双差操作;φ表示以m为单位的相位观测值;ρ表示接收机和卫星之间的几何距离;dρ表示卫星星历误差;λ表示载波相位波长;N表示整周模糊度;dion、dtrop、dφm分别表示电离层、对流层以及多路径误差;ε
表示双差操作;φ表示以m为单位的相位观测值;ρ表示接收机和卫星之间的几何距离;dρ表示卫星星历误差;λ表示载波相位波长;N表示整周模糊度;dion、dtrop、dφm分别表示电离层、对流层以及多路径误差;ε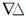 φ表示未模型化的误差及双差相位观测方程噪声。
φ表示未模型化的误差及双差相位观测方程噪声。
假设GPS双频基准站的个数为3,分别用下标1、2、3表示。由于基准站的坐标精确已知,因此几何距离计算中可以认为没有误差,又因轨道误差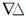 dρ在双差之后可以忽略不计,且基准站一般设立在开阔区,并采用抑径板天线,因此多路径误差
dρ在双差之后可以忽略不计,且基准站一般设立在开阔区,并采用抑径板天线,因此多路径误差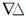 dmpφ也可忽略。则三个基准站之间组成两条独立基线的双差残差为:
dmpφ也可忽略。则三个基准站之间组成两条独立基线的双差残差为:
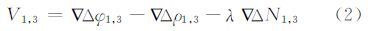
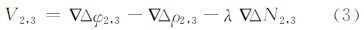
令移动站下标为u,则移动站和基准站3形成的双差相位观测方程为:
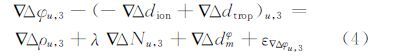
根据基准站和移动站的站点分布示意图可知,移动站所在基线的误差可以通过两条基准站基线的残差加以改正。改正后的移动站基线相位双差观测方程为:
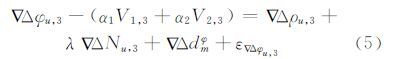
参数αi满足如下条件:
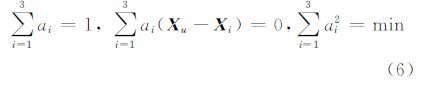
式中,Xu表示移动站坐标向量;Xi表示基准站坐标向量。则移动站u与基准站3组成的双差相位观测方程的误差改正项为α1V1,3+α2V2,3。令变形监测区域内的任意两个监测站点为j、k,则可以在这两个监测站点之间组成双差观测方程:
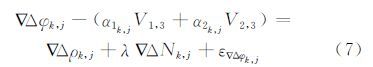
式中,αik,j表示测站j、k的ai之差。
由式(5)可知,假设V1,3和V2,3的误差不相关且都为σv,则通过区域大气延迟误差改正后的观测方程误差为:
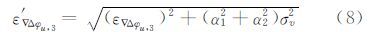
式中,ε′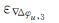 为改正后的双差观测方程误差;ε
为改正后的双差观测方程误差;ε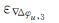 为原始双差观测方程的误差。式(8)是一个比较简化的推导结果,但是能在一定程度上反应出改正后的观测方程误差与α1和α2的关系,即α12+α22越小,改正后的观测方程误差越小。因此,在后续的实验中笔者采用两种布站方案,分别通过不同的组基线方式改变α12+α22,并比较最终的定位精度。
为原始双差观测方程的误差。式(8)是一个比较简化的推导结果,但是能在一定程度上反应出改正后的观测方程误差与α1和α2的关系,即α12+α22越小,改正后的观测方程误差越小。因此,在后续的实验中笔者采用两种布站方案,分别通过不同的组基线方式改变α12+α22,并比较最终的定位精度。
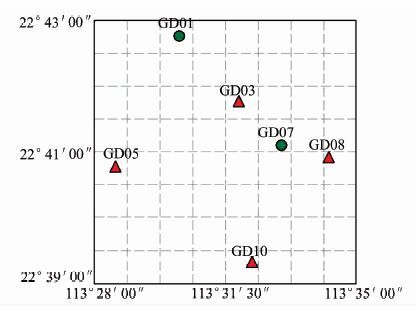
实验数据来源于广州南沙GPS地面沉降监测网络的实时观测数据,站点分布如图 2所示。其中,三角形表示双频基准站点(GD03,GD05,GD08,GD10),圆点表示单频监测站点(GD01,GD07)。实验数据采用电离层活跃年份2013-04-01~07-01连续3 mon(年积日091~181)数据,数据采样间隔为20 s。
|
| 图 2 实验数据站点分布图 Fig. 2 GPS Station Locations of Experimental Data |
在本文实验中,把直接采用传统双差解算未进行其他改正的方法称为直接双差方法,在单双频混合模式中采用了两种方案进行实验。方案1中采用GD05-GD03基线(5.9 km)和GD05-GD08基线(9.7 km)生成区域大气延迟误差,并改正单频站点GD01和GD07,其中,GD07站点位于该组三个基准站围成的三角形区域内,而GD01站点位于区域之外。方案2中采用GD08-GD03基线(4.4 km)和GD08-GD10基线(4.6 km)生成区域大气延迟误差,并改正单频站点GD01和GD07,其中,GD07站点位于该组三个基准站围成的三角形区域内,而GD01站点位于区域之外。
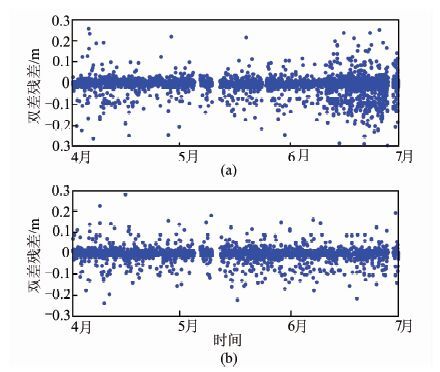
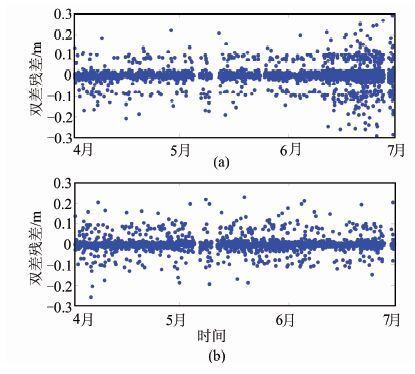
根据式(2)和式(3),分别计算方案1和方案2的大气延迟误差残余量。双频基准站的坐标采用Bernese 5.0解算获取的网解,因此认为精度足够可靠。本文实验中基准站间的双差整周模糊度确定过程为:首先确定双差宽巷模糊度,再确定窄巷模糊度,最后分别确定L1和L2的双差模糊度,具体理论推导过程参见文献[13, 14]。笔者采用自编数据处理软件[15]进行解算,双差残差信息如图 3和图 4所示。图 3所示为方案1中L1载波相位双差残差结果,其中,图 3(a)表示GD05-GD03基线L1载波相位双差残差,图 3(b)表示GD05-GD08基线L1载波相位双差残差。图 4所示为方案2中L1载波相位双差残差结果,其中,图 4(a)表示GD08-GD03基线L1载波相位双差残差,图 4(b)表示GD08-GD10基线L1载波相位双差残差。图 3、4中序列存在间断是由于监测过程中各种因素导致的数据缺失。比较图 3和图 4可以看出,在电离层活跃年份(2013年),处于低纬度地区(北纬22°左右)的GPS站尽管基线较短,经过双差差分之后,残余的大气延迟误差尤其是电离层残余误差仍较大,此时若不进行后续改正处理则会严重影响最终的基线解算结果。
|
| 图 3 方案1所有卫星L1载波相位双差残差 Fig. 3 Double-Differenced L1 Residuals for Scheme One |
|
| 图 4 方案2所有卫星L1载波相位双差残差 Fig. 4 Double-Differenced L1 Residuals for Scheme Two |
采用单双频混合处理模式,即在基线解算时添加基准站双频数据的双差改正信息,对上述数据进行解算获取了单天解坐标序列。为了能够更直观地显示沉降信息,本文把空间直角坐标(XYZ)转换到测站坐标(ENU)来描述。
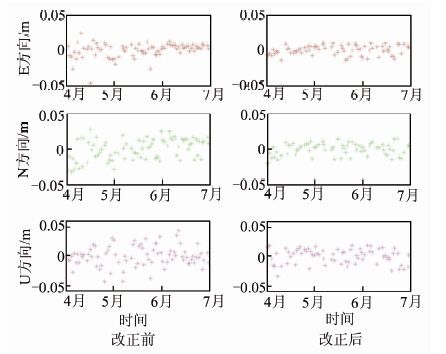
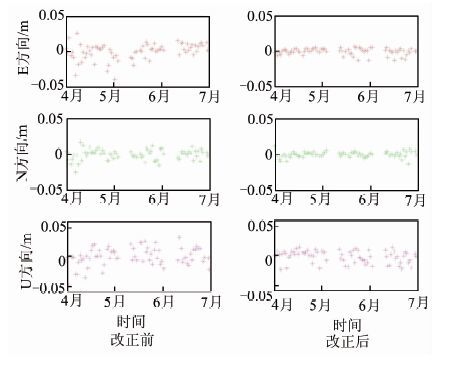
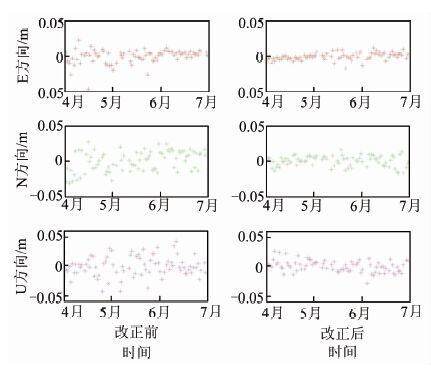
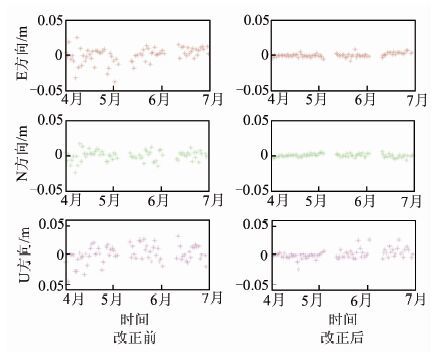
根据式(6)可计算出每个单频GPS站点相应的αi值,表 1所示为两种方案下计算出的GD01点和GD07点的α1和α2值。根据计算得到的αi值即可计算大气延迟误差残余量,再根据式(5)对单频数据进行改正。图 5和图 6分别表示方案1中GD01站点和GD07站点在经过区域大气延迟误差改正前后的单频解算结果对比图。图 7和图 8分别表示方案2中GD01站点和GD07站点在经过区域大气延迟误差改正前后的单频解算结果对比图。
由于此次广州南沙项目中的GPS接收机性能稍差导致观测数据质量不高,因此对定位精度有所影响,但从图 5,图 6,图 7,图 8中仍能得出部分有益的结论。从GD01站点的方案1和方案2(即图 5和图 7)可得出方案2的改正精度优于方案1,对比表 1的最后一列α12+α22的值可验证前面的原理论述部分,即α12+α22的值越小,添加区域大气延迟误差后的观测方程的噪声越小,从而更有利于提高后续的基线解算结果,这一结论同样从GD07站点的方案1和方案2(即图 6和图 8)可得到验证。再比较GD01站点和GD07站点的方案1改正信息(即图 5和图 6)可得出,对于同一种改正方案,由于GD07站点位于双频基准站组成的三角形区域内部,而GD01站点位于双频基准站组成的三角形区域外部,GD07站点的精度改善比例高于GD01站点,这一结论同样从GD01站点和GD07站点的方案2(图 7和图 8)中得到验证。
| 站点 | 方案 | α1 | α2 | α12+α22 |
| GD01 | 方案1 | 2.119 9 | -0.927 1 | 5.35 |
| 方案2 | 1.817 2 | -0.180 8 | 3.33 | |
| GD07 | 方案1 | 0.222 3 | 0.649 8 | 0.47 |
| 方案2 | 0.423 0 | 0.119 9 | 0.19 |
|
| 图 5 大气延迟误差残余量改正前后GD01定位 结果(方案1) Fig. 5 Results for GD01 Station Before and After Using Correction (Scheme 1) |
|
| 图 6 大气延迟误差残余量改正前后GD07 定位结果(方案1) Fig. 6 Results for GD07 Station Before and After Using Correction (Scheme 1 |
|
| 图 7 大气延迟误差残余量改正前后GD01定位 结果(方案2) Fig. 7 Results for GD01 Station Before and After Using Correction (Scheme 2) |
|
| 图 8 大气延迟误差残余量改正前后GD07定位结果(方案2) Fig. 8 Results for GD07 Station Before and After Using Correction (Scheme 2) |
为了更好地衡量坐标解算结果精度,在统计意义上可以通过坐标重复性的加权均方根[16, 17](weighted root mean square,WRMS)来进行评价。本文借鉴IGS组织评定坐标重复性标准,以周坐标重复性的WRMS为评价指标。表 2给出了基线解算时采用区域大气延迟误差残余量改正前后的WRMS统计信息对比,为了便于比较,在表 2中把α12+α22再次列出。从表 2中可以发现,采用单双频混合模式算法,单频数据在经过大气延迟误差残余量改正之后定位精度有明显改善。当单频站点位于双频站点组成的区域外部时,U方向改正后的WRMS优于1.01 cm,三维位置精度优于1.31 cm,精度改善达到37%;当单频站点位于双频站点组成的区域内部时,U方向改正后的WRMS优于0.66 cm,三维位置精度优于0.72 cm,精度改善达到58%。
| 站点 | 改正方案 | E分量/mm | N分量/mm | U分量/mm | 三维位置/mm | 三维位置改善比例 | α12+α22 |
| 不改正 | 8.1 | 12.6 | 14.6 | 20.9 | - | - | |
| GD01 | 方案1 | 6.1 | 7.8 | 12.4 | 15.9 | 24% | 5.35 |
| 方案2 | 4.4 | 7.2 | 10.1 | 13.1 | 37% | 3.33 | |
| 不改正 | 8.2 | 6.9 | 13.5 | 17.2 | - | - | |
| GD07 | 方案1 | 4.2 | 4.1 | 9.5 | 12.0 | 30% | 0.47 |
| 方案2 | 2.0 | 2.1 | 6.6 | 7.2 | 58% | 0.19 |
本文对低纬度的广州南沙地区(北纬22°左右)地面沉降监测网GPS实测数据进行了单双频混合模式数据处理,得出:(1)在电离层活跃区域,如果采用单频数据进行传统双差模式的差分处理并不能够完全消除大气延迟,尤其是电离层延迟误差;而通过变形监测区域外围的少数双频基准站观测数据解算获得的双差大气延迟改正项,对变形监测区域的单频数据进行改正后,定位精度将有明显改善,改正后U分量精度优于1.24 cm,三维位置精度优于1.59 cm,精度改善优于24%。(2)通过两种布站方案进行单双频混合实验,对比不同的双频基准站组网模式对监测站精度改善的性能,数值结果表明单双频混合GPS数据处理方法有助于提高单频数据解算精度,且当单频站点位于基准站组成的三角形区域内部时,改正效果尤为明显,U分量精度优于0.95 cm,三维位置精度优于1.2 cm,精度改善比例达到30%,最高可达58%。综上所述,采用单双频混合布网模式不仅有利于降低沉降监测中的费用支出,同时也保证了沉降监测的精度,具有一定的工程实践意义。
| [1] | Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan:Wuhan University Press, 2005(李征航, 黄劲松. GPS测量与数据处理[M]. 武汉:武汉大学出版社, 2005) |
| [2] | Zhu Jianjun, He Yueguang, Zeng Zhuoqiao, et al. Theories and Methods of Deformation Monitoring[M]. Changsha:Central South University Press, 2003(朱建军, 贺跃光, 曾卓乔,等. 变形监测的理论与方法[M]. 长沙:中南大学出版社, 2003) |
| [3] | Dong Longqiao. Application of GPS Technique in Regional Ground Settlement Monitoring[J]. Bulletin of Surveying and Mapping,2006(2):39-41(董龙桥. 应用GPS技术进行大面积地面沉降监测[J]. 测绘通报, 2006(2):39-41) |
| [4] | Abidin H Z, Andreas H, Djaja R, et al. Land Subsidence Characteristics of Jakarta Between 1997 and 2005, as Estimated Using GPS Surveys[J]. GPS Solutions, 2008,12(1):23-32 |
| [5] | Wang Li, Zhang Qin, Guan Jian'an, et al. Experiment Results and Analysis of the Dynamic Deformation Monitoring of a Kind of Landslide Based on GPS Technology[J]. Geomatics and Information Science of Wuhan University,2011, 36(4):422-426(王利, 张勤, 管建安, 等. 基于GPS技术的滑坡动态变形监测试验结果与分析[J]. 武汉大学学报·信息科学版, 2011, 36(4):422-426) |
| [6] | Li Zhenghang, Zhang Xiaohong. New Techniques and Precise Data Processing Methods of Satellite Navigation and Positioning[M]. Wuhan:Wuhan University Press, 2009(李征航, 张小红.卫星导航定位新技术及高精度数据处理方法[M]. 武汉:武汉大学出版社, 2009) |
| [7] | Li Ziwei, Chen Ruofu, Zhang Yong, et al. Preliminary Assessment of Experiential Ionosphere Model for Single Frequency GNSS Users in China Area[J]. Chinese Journal of Engineering Geophysics, 2009, 6(5):668-673(李子伟, 陈若夫, 张勇, 等. 区域单频GNSS用户经验电离层模型修正效果评估[J]. 工程地球物理学报, 2009, 6(5):668-673) |
| [8] | Tu Rui, Huang Guanwen, Zhang Qin, et al. A New Algorithm on Ionospheric Delay Correction for Single Frequency GPS Receivers[J]. Geomatics and Information Science of Wuhan University,2012, 37(6):667-670(涂锐, 黄观文, 张勤, 等. GPS单频机电离层延迟改正新算法[J]. 武汉大学学报·信息科学版, 2012, 37(6):667-670) |
| [9] | Deng Z, Bender M, Zus F, et al. Validation of Tropospheric Slant Path Delays Derived from Single and Dual Frequency GPS Receivers[J]. Radio Science, 2011, 46(6), DOI:10.1029/2011RS004687 |
| [10] | Zou X, Deng Z, Ge M. GPS Data Processing of Networks with Mixed Single and Dual-Frequency Receivers for Deformation Monitoring[J]. Advances in Space Research, 2010,46(2):130-135 |
| [11] | Han S, Rizos C. GPS Network Design and Error Mitigation for Real-Time Continuous Array Monitoring Systems[C]. ION GPS, Kansas City, MO, 1996 |
| [12] | Janssen V, Roberts C, Rizos C, et al. Low-Cost GPS-Based Volcano Deformation Monitoring at Mt. Papandayan, Indonesia[J]. Journal of Volcanology and Geothermal Research, 2002, 115(1):139-151 |
| [13] | Tang Weiming, Liu Jingnan, Shi Chuang, et al. Three Steps Method to Determine Double Difference Ambiguities Resolution of Network RTK Reference Staion[J]. Geomatics and Information Science of Wuhan University,2007, 32(4):305-308(唐卫明, 刘经南, 施闯,等. 三步法确定网络RTK基准站双差模糊度[J]. 武汉大学学报·信息科学版, 2007, 32(4):305-308) |
| [14] | Zhu Huizhong, Liu Jingnan, Tang Weiming, et al. The Algorithm of Single-Epoch Integer Ambiguity Resolution Between Long-Range Network RTK Base Stations[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3):359-365(祝会忠, 刘经南, 唐卫明, 等. 长距离网络RTK基准站间整周模糊度单历元确定方法[J]. 测绘学报, 2012, 41(3):359-365) |
| [15] | Zhang Jinsheng, Kuang Cuilin, Xie Rong'an, et al. Software Design and Implementation for Automatic Deformation Monitoring by Using GPS[J]. Geotechnical Investigation & Surveying, 2013(8):67-70(张晋升, 匡翠林, 谢荣安, 等. GPS自动变形监测软件设计与实现[J]. 工程勘察, 2013(8):67-70) |
| [16] | Xu Ying. Research on the Stability of GPS Reference Station in Tianjin CORS[D]. Wuhan:Wuhan University, 2011(徐莹. 天津CORS参考站的位置稳定性研究[D]. 武汉:武汉大学, 2011) |
| [17] | Altamimi Z, Sillard P, Boucher C. ITRF2000:A new release of the International Terrestrial Reference Frame for Earth Science Applications[J]. Journal of Geophysical Research, 2002, 107(B10):2214-2221 |
 2016, Vol. 41
2016, Vol. 41


