文章信息
- 赵齐乐, 戴志强, 王广兴, 李晓涛, 刘经南
- ZHAO Qile, DAI Zhiqiang, WANG Guangxing, LI Xiaotao, LIU Jingnan
- 利用非差观测量估计北斗卫星实时精密钟差
- Real-Time Precise BDS Clock Estimation with the Undifferenced Observation
- 武汉大学学报·信息科学版, 2016, 41(5): 686-691
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 686-691
- http://dx.doi.org/10.13203/j.whugis20150314
-
文章历史
- 收稿日期: 2015-10-27

2. 武汉大学测绘学院, 湖北武汉, 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
北斗卫星导航系统(BeiDou satellite navigation system,BDS)是中国自主研发、独立运行的全球卫星导航系统。至2012年年底,我国的第二代北斗卫星导航系统已经具备了亚太地区的导航定位服务能力,在轨工作卫星包括5颗地球静止卫星(geostationary orbit,GEO)、5颗倾斜地球同步卫星(inclined geosynchronous orbit,IGSO)和4颗中轨卫星(medium altitude Earth orbit,MEO)。北斗卫星导航系统计划于2020年年底实现全球导航定位服务功能,届时全星座将包括5颗GEO、3颗IGSO和27颗MEO卫星[1]。精密钟差与轨道是卫星导航定位系统实现高精度定位的前提条件[2, 3],目前已有一些学者和国际GNSS服务(International GNSS Service,IGS)分析中心利用全球的北斗跟踪数据解算北斗事后精密钟差和轨道产品,并成功地应用于北斗事后精密定位[4, 5]。但是,北斗只提供事后产品,并不能实现完整的服务目标,还需为实时精密定位用户提供高精度的实时产品。卫星的轨道具有可预报性,在进行精密定轨的同时能对轨道进行预报。现有的一些北斗精密轨道也包含预报轨道,并能达到很好的精度,可应用于实时定位。由于导航卫星原子钟易受外界及本身因素的影响,变化极为复杂,很难利用数学模型进行预报,必须利用地面跟踪网的实时观测数据进行实时估计[6]。IGS及其下属的分析中心早已为GPS和全球导航卫星系统(global navigation satellite system,GLONASS)提供实时钟差产品并通过网络播发,但北斗系统尚没有实时钟差产品。生成高精度的北斗实时钟差对提升北斗应用服务水平具有重要意义。实时钟差估计多采用历元间差分方法,以提高处理效率,保证钟差产品的实时性。通过在历元间求差,能够消除大量的模糊度参数,只保留数量相对较少的卫星钟差、接收机钟差和对流层参数,因此其处理效率较高[7, 8]。近年来有学者研究了基于非差观测量的实时钟差估计以及非差和双差混合差分的钟差估计方法。利用非差观测量进行实时钟差估计能够保留模糊度参数,为后续双差模糊度固定和卫星硬件延迟估计提供可能[9, 10]。本文介绍了基于非差观测量的北斗实时钟差估计算法和数据处理过程,利用根据该算法实现的软件处理了多模GNSS实验跟踪网(multi-GNSS experiment,MGEX)的北斗观测数据,生成北斗实时钟差产品,并分析了产品的精度和定位性能。
1 基于非差观测量的实时精密钟差估计算法
1.1 观测模型
本文采用非差消电离层组合观测量进行精密钟差估计,对应的伪距与相位观测量可以模型化为:
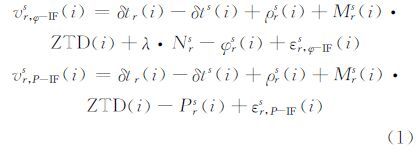
其中,r、s和i分别对应测站、卫星和观测历元的编号;δtr(i)和δts(i)分别表示接收机钟差和卫星钟差;ZTD(i)是天顶对流层延迟;Mrs(i)是对应测站r和卫星s的投影函数;λ和Nrs为消电离层相位组合观测量的波长和模糊度;ρrs(i)表示信号发射时刻的卫星位置与信号接收时刻接收机位置间的几何距离;φrs(i)和Prs(i)分别表示以m为单位的相位与伪距的消电离层观测量,vr,φ-IFs(i)和vr,P-IFs(i)是对应的残差;εr,φ-IFs(i)和εr,P-IFs(i)是相位与伪距观测量的测量噪声。
不同于历元间差分模型求解各个历元的钟差变化率(需配合初始钟差),基于式(1)的钟差估计模型能给出每个历元的绝对钟差。由于没有在历元间作差,非差方法前后历元观测量间不存在相关性,同时求解的是绝对对流层延迟,能较准确地分离对流层误差。另一方面,该模型保留了模糊度参数,虽然后续能基于此进行模糊度固定,但此类参数数量较大,会增加软件的处理时间,降低时效性,需对算法和软件进行优化。
1.2 非差实时钟差估计算法平方根信息滤波(square-root information filter,SRIF)是一种改进的卡尔曼滤波算法,其算法简单、数值稳定性高,特别适合进行实时精密数据处理。本文采用平方根信息滤波器对式(1)中的观测方程进行处理,实时估计卫星精密钟差等状态参数。平方根信息滤波包含测量更新和时间更新两步,对应于历元i的SRIF更新算法为[11]:
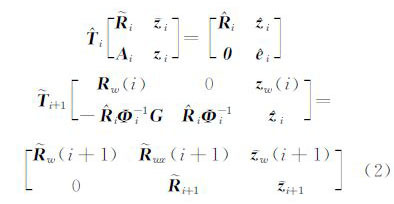
其中,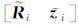 是由前面i-1个历元得到的参数的先验信息;[Ai zi]是当前历元所有可用观测量按式(1)线性化后的观测方程矩阵;
是由前面i-1个历元得到的参数的先验信息;[Ai zi]是当前历元所有可用观测量按式(1)线性化后的观测方程矩阵;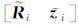 是利用当前历元观测量进行测量更新后得到的参数信息;[Rw(i)zw(i)]是参数的过程噪声信息;
是利用当前历元观测量进行测量更新后得到的参数信息;[Rw(i)zw(i)]是参数的过程噪声信息;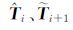 是Householder正交变换矩阵;Φi、G是状态方程中对应状态向量和过程噪声的系数阵。
是Householder正交变换矩阵;Φi、G是状态方程中对应状态向量和过程噪声的系数阵。
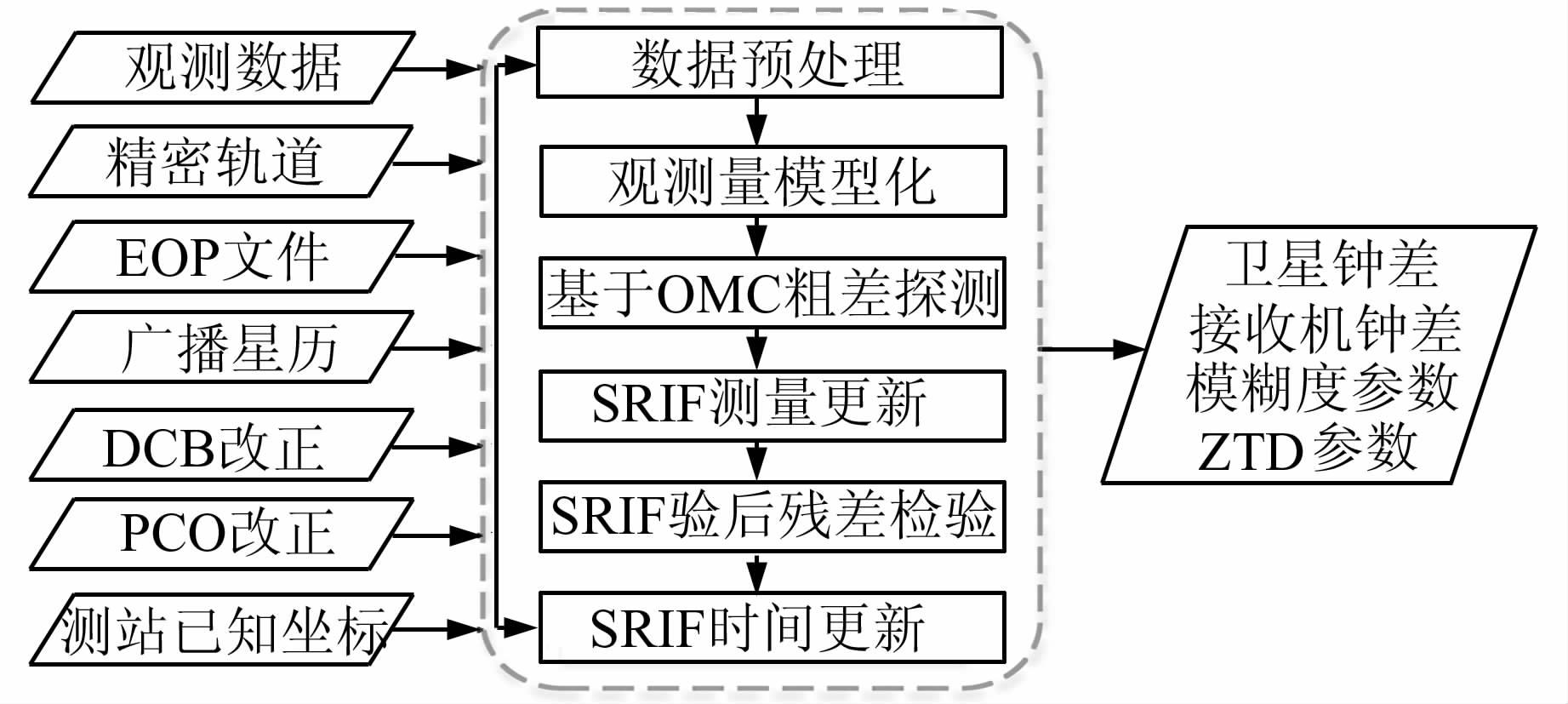
本文数据处理软件具体实现的流程如图 1所示。
|
| 图 1 基于非差观测量的实时钟差估计流程 Fig. 1 Flowchart of the Algorithm of Real-Time Precise Clock Correction Estimation with Undifferenced Observations |
图 1中,左边显示的是输入数据,包括北斗与GPS观测数据、精密轨道、地球定向参数(Earth orientation parameters,EOP)文件、广播星历、码偏差(differential code bias,DCB)改正、天线相位中心(phase center offset,PCO)改正和测站已知坐标等;中间是实时钟差估计软件的组成模块和处理流程,数据处理模块主要是基于式(1)的所有观测量的线性方程进行SRIF测量更新和时间更新,为了剔除观测量中粗差的影响,在不同的阶段会对观测量进行质量控制,主要包括数据预处理、基于验前残差(observation minus computation,OMC)的粗差探测和SRIF验后残差检验。图 1中,右边是实时处理软件的输出结果。
2 数据实验与结果分析
2.1 实验数据准备与解算策略
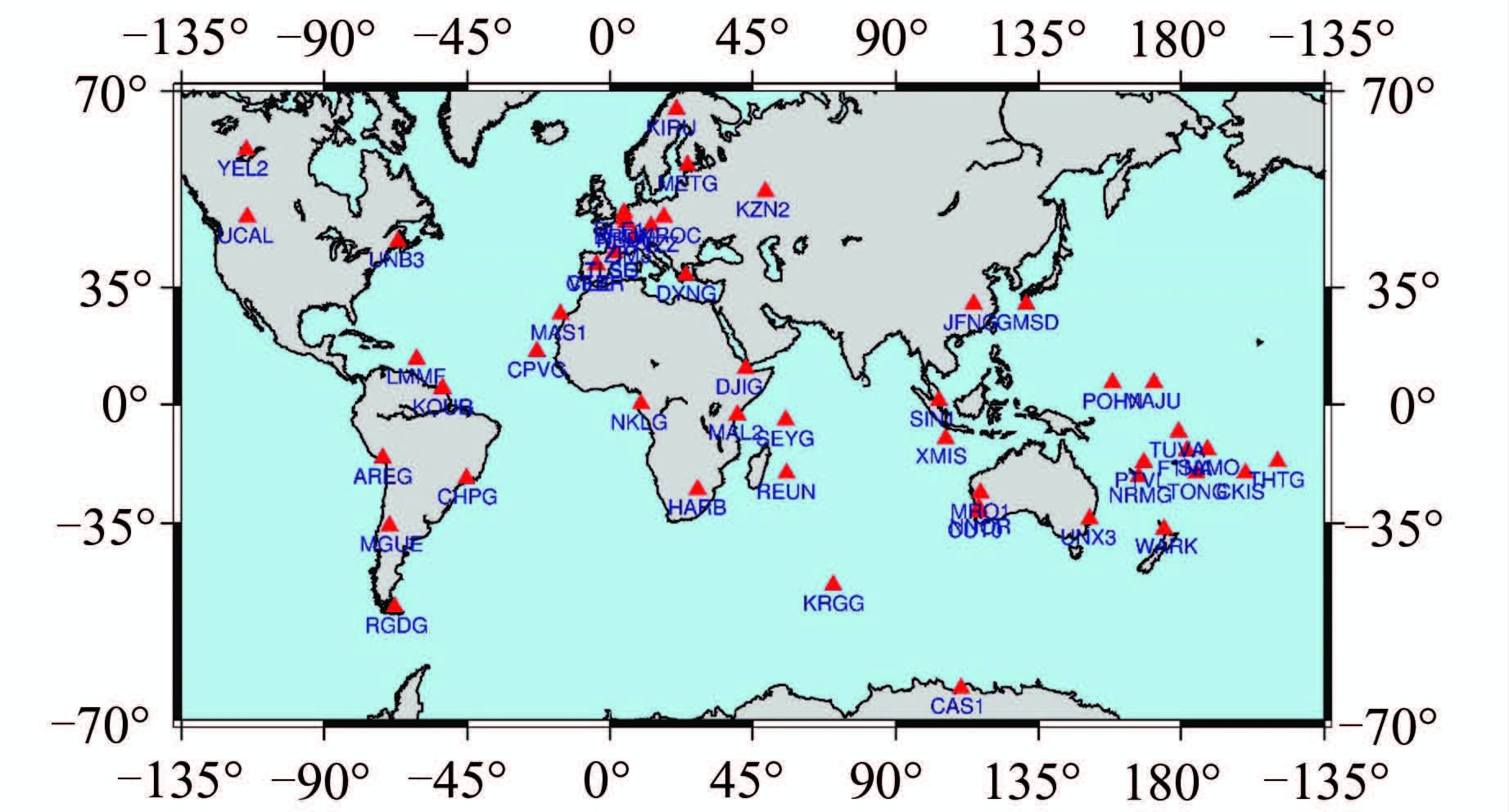
在精密数据处理软件PANDA的基础上对上述算法进行了编程实现,形成了一套实时钟差估计软件[12]。为了验证非差实时钟差估计算法的性能,本文选取了2015年001~060天全球 53个MGEX站的GPS和北斗观测数据进行实时钟差估计,并对生成的钟差产品进行统计分析,这些测站的分布如图 2所示。
|
| 图 2 用于实时钟差估计的53个MGEX测站分布图 Fig. 2 Distribution of the 53 MGEXSites Used in Real-Time Clock Estimation |
由于北斗系统目前尚未完全建成,MEO卫星较少且卫星分布不均匀,亚太地区的测站能观测到较多的北斗卫星,而欧洲和美洲地区只能观测到很少的北斗卫星,有时甚至完全观测不到卫星。如果测站观测到的卫星数较少,对流层延迟、接收机钟差与卫星钟差就较难分离,影响钟差估计的精度。因此,本文同时估计北斗和GPS卫星的实时钟差,既增加了单个测站的观测量有助于参数分离,也能利用GPS实时钟差进行对比分析。本文在进行实时钟差估计时,软件具体的参数配置与处理策略如表 1所示。
| 参数类型 | 模型配置 | |
| 观测量 | 观测量 | LC、PC组合非差观测量 |
| 先验约束 | GPS L1:伪距1.0 m,相位0.006 m BDS B1: 伪距2.0 m,相位0.02 m | |
| 截止高度角 | 10° | |
| 观测量加权 |
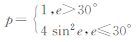
| |
| 误差改正 | 相位缠绕 | 模型改正 |
| 相位中心变化 | IGS08模型 | |
| 大气负荷 | 不考虑 | |
| 潮汐改正 | 固体潮、极移潮、海洋潮汐 | |
| 卫星相位中心 | 绝对相位中心 | |
| 相对论改正 | 模型改正 | |
| 参数估计 | 参考钟 | 固定一个接收机钟(按顺序选取CUT0、SIN1、JFNG、DJIG和GMSD中的一个接收机钟作为参考钟,余下的作为备选参考钟) |
| 卫星轨道 | WHU精密轨道 | |
| 测站坐标 | 固定为IGS周解 | |
| EOP | 固定为IERS解 | |
| 对流层 | Saastamoine模型 + 随机游走 | |
| 卫星钟差 | 广播星历钟差 + 白噪声 | |
| BDS与GPS系统间偏差 | 伪距估计 + 白噪声 | |
| 接收机钟差 | 伪距估计 + 白噪声 | |
| 模糊度 | 估计 |
评估钟差精度时常选取已知精度更高的钟差产品作为参考,计算对应时刻待评估钟差相对于参考钟差的差异,利用该差异统计其精度。不同的软件估计钟差时选取的钟差基准并不相同,因此,两套钟差的差异中还包含各自钟差基准的偏差。基准偏差对于所有卫星都相同,并不反映钟差的精度,常采用二次差方法消除基准偏差后进行钟差精度评定[13]。本文稍作改进,通过当前历元所有卫星的钟差差异取平均得到基准偏差,并从各个卫星的钟差差异中扣除,这样可以避免当参考星钟差出现大的偏差时影响评估结果。具体公式为:
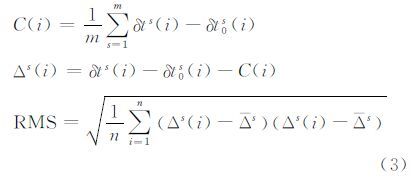
式中,δts(i)、δt0s(i)分别是第i个历元卫星s的实时钟差和武汉大学的事后精密钟差;C(i)是由该历元m颗卫星的钟差差异取平均得到的基准偏差;Δs(i)是消除基准偏差后的钟差差异;Δs是Δs(i)的均值;RMS反映钟差的精度。
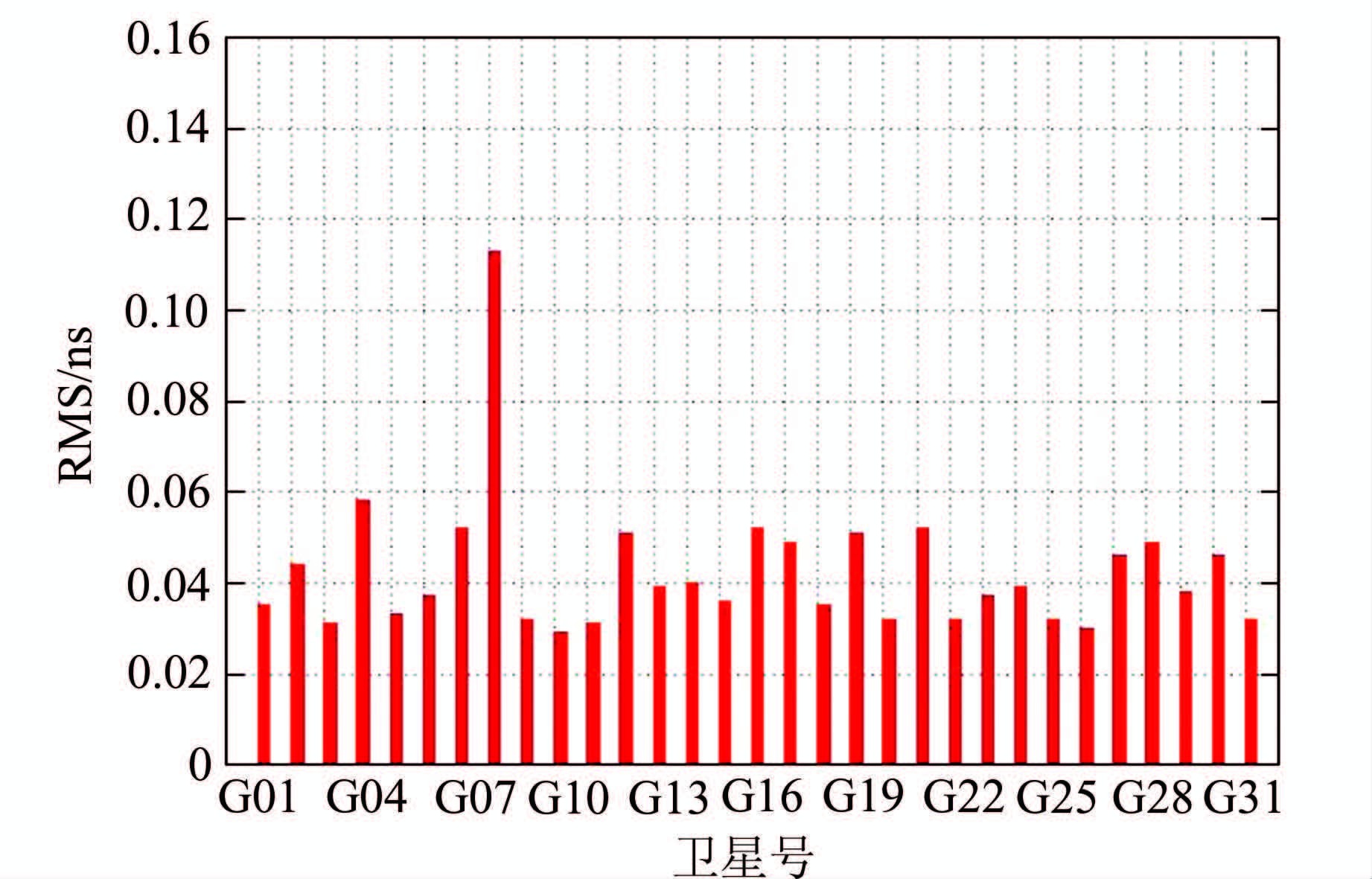
武汉大学GPS中心作为IGS分析中心之一,目前已能提供GPS、GLONASS、GALILEO和北斗4系统精密轨道与钟差产品,其GPS事后精密钟差与IGS及各个分析中心的产品具有相当的精度[4]。为了分析武汉大学事后钟差产品作为参考钟差的可靠性,本文首先比较了2015年001~060天期间武汉大学与IGS的GPS事后30 s钟差产品的精度。利用式(3)逐天比较各颗卫星的钟差精度,在这期间由于卫星更新,G26卫星大部分时间没有钟差产品,故没有分析。图 3所示的是两个钟差产品中各颗卫星在2015年001~060天期间每天RMS的平均值。从图 3中可以看出,除G08较大外,其他卫星的差异均小于0.06 ns,该差异与IGS事后钟差产品的精度相当,说明武汉大学的事后钟差产品可以作为评价实时钟差产品的参考钟。北斗卫星的各类改正模型(如PCO、偏航姿态等)仍在研究之中,各个分析中心在数据处理过程中使用的模型并没有统一,因此,目前尚不能很好地评估不同分析中心的北斗钟差产品。本文在估计北斗实时钟差时使用的模型与武汉大学的事后钟差保持一致,因此可以采用武汉大学的北斗事后钟差作为参考来评估北斗实时钟差的精度。
|
| 图 3 2015年001~060天期间武汉大学GPS事后 Fig. 3 Mean RMS of 30 s GPS Precise Final Clock of WHU and IGS During 001~060,2015 |
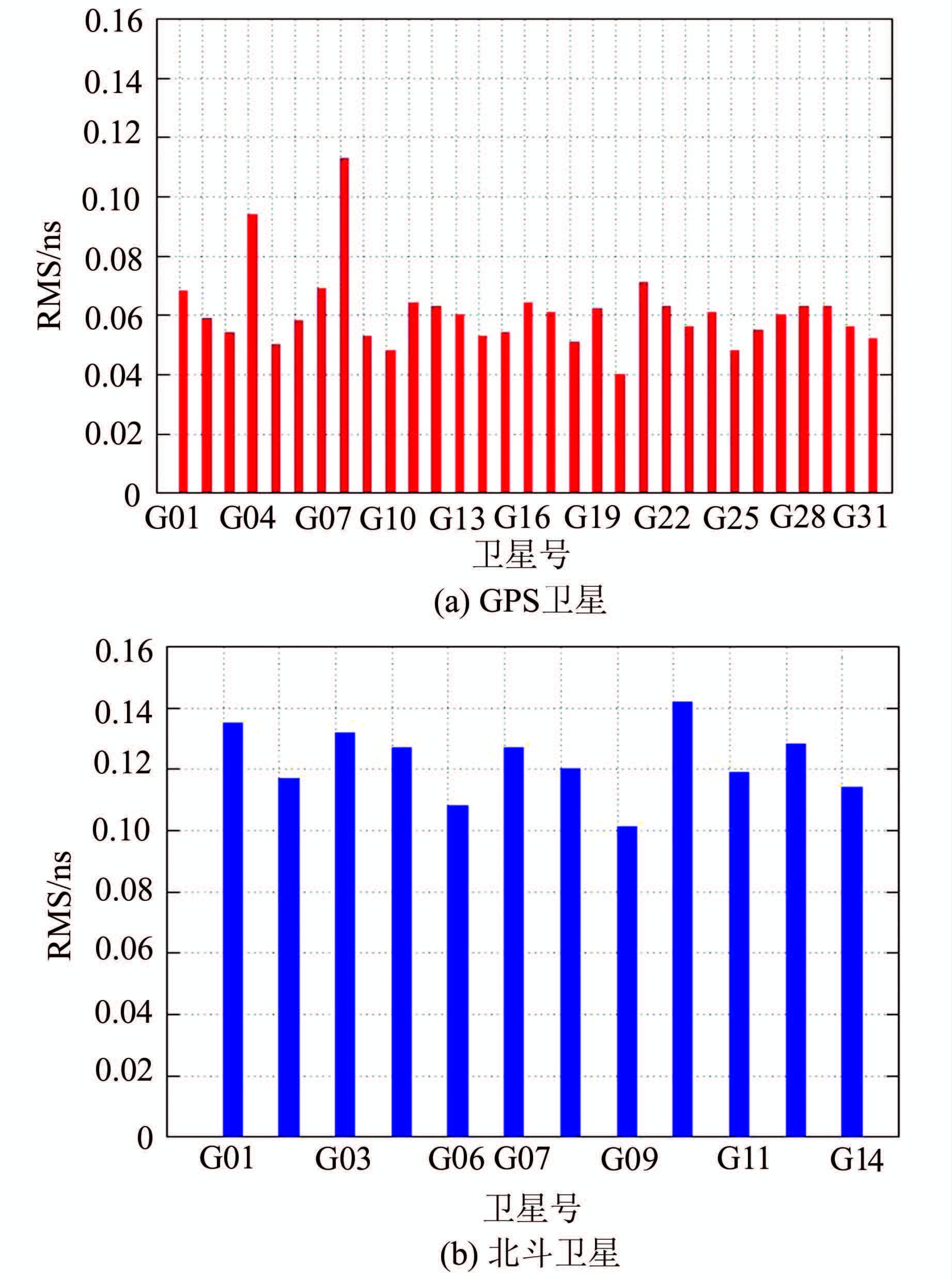
在实时数据处理期间,G26卫星大部分时间没有观测值,C05卫星观测值的质量较差,C13卫星完全没有观测值,故没有生成这三颗卫星的实时钟差产品。其他卫星的实时钟差产品采用同样的方法以武汉大学事后30 s精密钟差作为参考逐天评估精度。图 4所示的是数据处理期间各颗卫星实时钟差RMS的平均值。从图 4(a)中可以看出,GPS实时钟差与事后钟差符合较好,除G04和G08外,其他卫星的钟差精度均优于0.07 ns,略低于事后钟差。该结果表明了本文实时钟差估计软件具有较高的估计精度。从图 4(b)中可以看出,所有北斗卫星的钟差精度介于0.1~0.15 ns之间,略低于GPS卫星的精度。北斗卫星实时钟差精度较GPS低,这可能跟卫星数量和测站分布有关,后期需进行深入研究。
|
| 图 4 2015年001~060天期间GPS和北斗实时钟差与武汉大学事后30 s精密钟差比较的RMS的平均值 Fig. 4 Mean RMS of GPS and BDS Real-Time Clock Compared to the WHU 30 s Final Clock Product During 001~060,2015 |
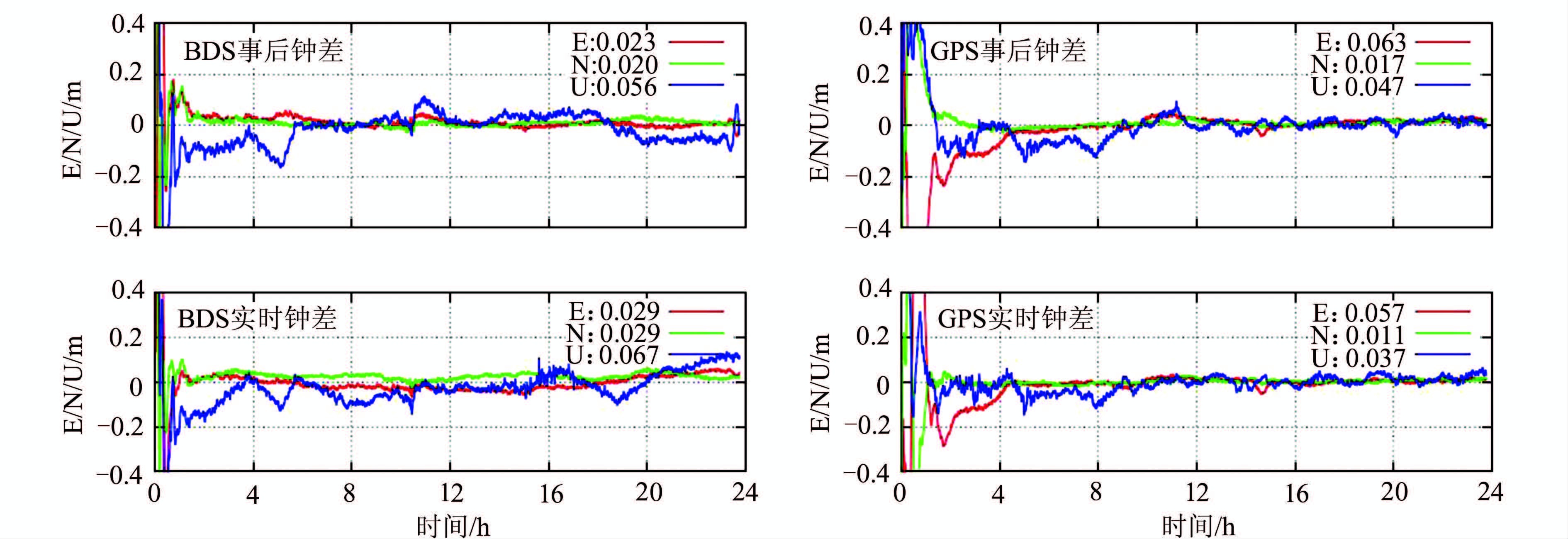
利用实时钟差产品对静态观测数据进行模拟动态精密单点定位(precise point positioning,PPP)解算,并将定位结果与已知精确坐标进行比较,进一步验证了本文生成的实时钟差的定位性能。图 5所示的是分别利用武汉大学事后30 s钟差和实时钟差对XMIS站(-10.45° N,105.69° E),具有较好的GPS与北斗观测条件的GPS和北斗观测数据进行模拟动态PPP实验的结果。在定位收敛之后,基于事后钟差产品的GPS与北斗定位结果在E、N、U三个方向上的精度分别为GPS:0.063 m、0.017 m、0.047 m,北斗:0.023 m、0.020 m、0.056 m;基于实时钟差产品的GPS与北斗定位结果在E、N、U 三个方向上的精度分别为GPS:0.057 m、0.011 m、0.037 m,北斗:0.029 m、0.029 m、0.067 m。从图 5中可以看出,GPS和北斗基于各自实时钟差的定位结果与对应基于事后钟差的结果符合得很好,说明实时钟差与事后钟差差异不大。其中,GPS的实时钟差解略优于事后钟差解,而北斗则相反,这可能是因为GPS的实时钟差与事后钟差差异很小,且实时钟差解算与动态PPP定位使用同一套程序,模型完全一致,而北斗实时钟差的精度低于GPS,与事后钟差的差异稍微大一些。GPS和北斗在N方向的定位精度差异不大,在E方向上,GPS的定位精度略低于北斗。分析发现,该站在前5 h观测到的可用GPS卫星平均为9颗,且卫星数波动较大,最少时只有7颗,而同一时段内可用的北斗卫星平均为11颗,并能在很长一段时间内观测到11颗北斗卫星,这造成了GPS定位结果在E方向收敛较慢、精度较北斗低。在U方向上,北斗的定位精度则低于GPS,这可能由两方面的原因造成,一是北斗的钟差(事后或实时)精度低于GPS,另一方面北斗GEO卫星观测量中的对流层延迟较难分离。随着MEO卫星数量的增加,北斗的实时定位精度将会进一步提高。
|
| 图 5 利用武汉大学事后30 s钟差与实时钟差分别进行GPS与北斗模拟动态PPP定位的结果 Fig. 5 GPS and BDS Kinematic PPP Solutions Based on the WHU 30 s Final Clock and Real-Time Clock |
本文介绍了基于非差观测量的实时钟差估计算法,包括观测方程、实时滤波器和处理流程,并基于PANDA软件实现了该算法。选取了53个MGEX站的北斗与GPS数据进行实时钟差估计,根据钟差估计结果分析了软件的处理精度和产品的定位性能。统计分析表明,本文生成的GPS实时钟差与事后钟差符合较好,精度优于0.07 ns,略低于事后钟差产品,验证了本文实时钟差估计软件的处理精度。本文解算的北斗实时钟差的精度介于0.1~0.15 ns之间,低于GPS卫星的精度。基于实时钟差进行模拟动态PPP实验,北斗与GPS在水平方向的定位精度为0.041 m和0.058 m,高程方向的精度为0.069 m和0.037 m,定位结果分别与事后钟差的结果符合很好,表明实时钟差与事后钟差差异不大。
非差模型能较好地分离对流层误差,实现较高的钟差估计精度,同时也保留了模糊度参数,后续可研究利用双差模糊度约束提高实时钟差估计的精度。然而,利用非差观测量进行实时钟差估计时,除了要估计卫星钟差、接收机钟差和对流层参数外,还会有大量的模糊度参数,当测站数和卫星数增加时(如100个全球测站,多系统观测数据等),其时效性会降低。后续一方面可以研究实时固定双差模糊度来提高钟差估计精度,另一方面还要对算法和程序进行优化,必要时对核心处理模块进行并行化,以提高处理效率,满足实时性要求。
| [1] | Shi Chuang, Zhao Qile, Hu Zhigang, et al. Precise Relative Positioning Using Real Tracking Data from COMPASS GEO and IGSO Satellites[J]. GPS Solut, 2013, 17(1):103-119 |
| [2] | Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. J Geophys Res Solid Earth, 1997, 102:5005-5017 |
| [3] | Ye Shirong. Theory and Its Realization of GPS Precise Point Positioning Using Un-differenced Phase Observation[D]. Wuhan:Wuhan University, 2002(叶世榕. GPS非差相位精密单点定位理论与实现[D]. 武汉:武汉大学, 2002) |
| [4] | Zhao Qile, Guo Jing, Li Min, et al. Initial Results of Precise Orbit and Clock Determination for COMPASS Navigation Satellite System[J].GPS Solut, 2013, 87(5):475-486 |
| [5] | Li M, Qu L, Zhao Q, et al. Precise Point Positioning with theBeiDou Navigation Satellite System[J]. Sensors, 2014, 14:927-943 |
| [6] | Li Haojun, Wang Jiexian, Wang Hu, et al. Precise Clock Error Estimation of GPS Satellite and Analysis Based on GNSS Network[J]. Geomatics and Information Science of Wuhan University, 2010, 35(8):1001-1003(李浩军, 王解先, 王虎, 等. 基于GNSS网络的卫星精密钟差估计及结果分析[J]. 武汉大学学报·信息科学版, 2010, 35(8):1001-1003) |
| [7] | Ge M, Chen J, DouŠa J, et al. A Computationally Efficient Approach for Estimating High-Rate Satellite Clock Corrections in Realtime[J]. GPS Solut, 2012, 16:9-17 |
| [8] | Zhang X, Li X, Guo F. Satellite Clock Estimation at 1 Hz for Realtime Kinematic PPP Applications[J]. GPS Solut, 2011, 15:315-324 |
| [9] | Li Xingxing, Xu Yun, Wang Lei. Undifferenced Precise Satellite Clock Error Estimation and Precision Analysis[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6):661-664(李星星, 徐运, 王磊. 非差导航卫星实时/事后精密钟差估计[J]. 武汉大学学报·信息科学版, 2010, 35(6):661-664 |
| [10] | Hauschild A, Montenbruck O. Kalman-Filter-Based GPS Clock Estimation for Near Real-Time Positioning[J]. GPS Solut, 2009, 13:173-182 |
| [11] | Bierman G J. Factorization Methods for Discrete Sequential Estimation[M]. New York:Dover Publications, 2006 |
| [12] | Zhao Qile. Research on Precise Orbit Determination Theory and Software of both GPS Navigation Constellation and LEO Satellites[D]. Wuhan:Wuhan University, 2014(赵齐乐. GPS导航星座及低轨卫星精密定轨理论和软件研究[D]. 武汉:武汉大学, 2014) |
| [13] | Lou Yidong, Shi Chuang, Zhou Xiaoqing, et al. Realization and Analysis of GPS Precise Clock Products[J]. Geomatics and Information Science of Wuhan University, 2009, 34(1):88-91(楼益栋, 施闯, 周小青, 等. GPS精密卫星钟差估计与分析[J]. 武汉大学学报·信息科学版, 2009, 34(1):88-91) |
 2016, Vol. 41
2016, Vol. 41



