文章信息
- 田晶, 武晓环, 林镠鹏, 任畅
- TIAN Jing, WU Xiaohuan, LIN Liupeng, REN Chang
- 城市道路网的度相关性及其与网络鲁棒性的关系研究
- Degree Correlation of Urban Street Networks and Its Relationship with Network Robustness
- 武汉大学学报·信息科学版, 2016, 41(5): 672-678
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 672-678
- http://dx.doi.org/10.13203/j.whugis20150046
-
文章历史
- 收稿日期: 2015-05-17

2. 武汉大学地理信息系统教育部重点实验室, 湖北武汉, 430079;
3. 数字制图与国土信息应用工程国家测绘地理信息局重点实验室, 湖北武汉, 430079
2. Key Laboratory of Geographic Information System, Ministry of Education, Wuhan University, Wuhan 430079, China;
3. Key Laboratory of Digital Mapping and Land information Application Engineering, National Administration of Surveying, Mapping and Geoinformation, Wuhan 430079, China
随着新网络科学以及自发地理信息的发展[1],道路网的拓扑分析迎来了新的发展机遇。前者为其提供了分析的理论与方法,后者为其提供了丰富的数据。与复杂网络应用的其他领域类似,相对于关注得较多的无标度和小世界网络[2, 3],道路网的度相关性关注较少。现实世界中的一些网络呈现出度高的节点倾向于与度高的节点相连的现象,表现为度相关性的同配,如演员合作网络和论文合作网络。另外一些网络呈现出度高的节点倾向于与度低调节点相连的现象,表现为度相关性的异配,如互联网和神经网络。还有一些既不呈现同配,也不呈现异配的网络,如Erds-Rényi随机图[4]。对于道路网这一类地理网络,它的度相关性呈现同配还是异配是值得研究的问题。Porta等运用平均最近邻度对世界范围内的6个城市中1 km2范围内的道路网进行了研究,得出道路网并非同配网络的结论[5]。Buhl等 运用Newman同配性系数对欧洲41个自组织城市进行研究发现绝大多数城市道路网都是异配网络[6]。Masucci等运用运用平均最近邻度对London道路网进行了度量,发现低度节点倾向异配,高度节点呈现不相关[7]。田晶等运用Newman同配性系数对美国40个道路网进行了度量,虽然在绝对的数值上有正负,然而均接近于0,即度近似于不相关[8]。上述研究在数据样本及度相关性的度量方面存在一定问题。在数据样本方面,样本的数量有单一和多个两种;样本来源的区域有世界范围、美国和欧洲,样本的幅度有城市内1 km2的范围、城市中的部分路网,以及整个城市路网。具有相对异质性的样本,其幅度太小,幅度为整个城市的样本其来源较为单一。在度相关性的度量方面,目前主要采用平均最近邻度曲线和Newman同配性系数,平均最近邻度通过看图像进行判断,具有一定的主观性及不易辨识性。有研究指出Newman同配性系数会随着网络的尺寸减小,建议运用Litvak-Hofstad 同配性系数[9]。世界范围内的大规模复杂道路网的度相关性如何是本文关注的第一个问题。
根据网络表达不同,道路网拓扑分析的方法主要有原图法与对偶法两种。原图法指图的节点对应于道路交叉点,图的边对应于道路段;对偶法指图的节点对应于道路段或Stroke,图的边对应于道路段或Stroke间是否具有相交关系。近期出现了基于Community建立对偶图的新思路[10],然而常用的仍是基于Stroke构建对偶图。Stroke的概念源于Gestalt认知原则中好的连续律[11],也有学者称其为自组织自然道路[12, 13]。由此表示的对偶图形式超脱了原有网络的几何表示,更关注于其拓扑组织,有助于揭示隐含结构[1]。生成道路网的Stroke是将道路网中满足好的连续律的路段连接到一起形成若干Stroke过程。在道路网拓扑分析领域,Stroke生成方法主要有两种:第一种是将同名道路连接[12],第二种是设定路段能否连接的角度阈值,运用每对最大适合策略(every-best-fit,EBF)、自身最大适合策略(self-best-fit,SBF)和自身适合策略(self-fit,SF)连接[13]。除此之外,在地图综合领域,还有考虑道路等级以及混合的方法[14]。由于道路名字和专题属性的缺失、误标等问题,拓扑分析中通常运用第二种生成方法。那么,对同一道路网,不同的Stroke生成方法会生成不同的Stroke集,采用同一方法,如采用SBF策略多次生成的Stroke集不同,这就导致了与“可塑性面单元”类似的“可塑性线性单元”问题[13]。由同一路网生成的不同Stroke集是否影响道路网度相关性的度量结果,这是本文试图回答的第二个问题。
复杂网络的鲁棒性研究当网络受到蓄意攻击或者出现随机故障时,网络中节点间的连接程度受到的破坏以及通信传输行为受到的影响[2]。蓄意攻击表现为删除网络中重要的节点或边,而随机故障表现为随机删除网络中的节点或边[2, 15]。对于道路网而言,恐怖袭击、灾害发生、交通拥堵都会影响网络的功能。有研究表明同配网络比异配网络具有更强的抵御能力[6, 16]。那么,对于道路网而言,是否具有这样的规律是本文拟研究的第三个问题。
本文以世界范围内的50个城市道路网作为实验数据,运用Newman同配性系数和Litvak-Hofstad同配性系数,对以Stroke对偶形式表达的道路网的度相关性进行了度量;同时,对同一路网不同Stroke集对道路网的度相关性度量的影响进行了分析;最后,对度相关性与鲁棒性的关系进行了研究。
1 数据及其预处理
自发地理信息的发展为大规模的地理分析提供了丰富的数据[17, 18],开放街道地图(OpenStreetMap,OSM)是其典型的成功案例。尽管OSM数据质量存在一定问题[19, 20, 21, 22],有学者认为其可与国家测绘地理信息部门提供的数据相媲美[23],而且已有很多成功应用[23, 24, 25, 26]。本文研究的数据为世界范围内的50个城市的道路网,这些城市的选取既考虑到了大洲分布、历史起源和城市规模,又结合OSM道路数据的完整性,其中欧洲22个、北美洲13个、亚洲8个、非洲3个、南美洲3个、大洋洲1个(见表 1)。
| 城市 | EBF | SBF | SF | |||||||||
| r | σr | ρ | σρ | r | σr | ρ | σρ | r | σr | ρ | σρ | |
| Bejaia | -0.042 | 0.029 | -0.118 | 0.041 | -0.041(11) | 0.031(5) | -0.116(11) | 0.041(0) | -0.036(14) | 0.034(5) | -0.104(13) | 0.041(0) |
| Osaka | -0.005 | 0.005 | -0.031 | 0.006 | -0.006(1) | 0.005(0) | -0.033(1) | 0.006(0) | -0.004(3) | 0.005(0) | -0.032(2) | 0.006(0) |
| Pittsburgh | -0.006 | 0.009 | -0.051 | 0.009 | -0.008(2) | 0.009(0) | -0.053(1) | 0.009(0) | -0.014(4) | 0.009(1) | -0.054(1) | 0.009(0) |
| | ||||||||||||
| Berlin | 0.004 | 0.004 | -0.129 | 0.004 | 0.003(1) | 0.004(0) | -0.132(1) | 0.004(0) | 0.000(2) | 0.004(0) | -0.133(1) | 0.004(0) |
| Curitiba | -0.008 | 0.006 | 0.022 | 0.007 | -0.009(3) | 0.006(0) | 0.021(1) | 0.007(0) | -0.009(3) | 0.006(0) | 0.022(2) | 0.007(0) |
| Harare | -0.001 | 0.014 | -0.162 | 0.013 | 0.001(2) | 0.014(0) | -0.162(1) | 0.013(0) | 0.003(2) | 0.014(0) | -0.161(1) | 0.013(0) |
| Reno | 0.008 | 0.012 | -0.123 | 0.013 | 0.007(1) | 0.012(0) | -0.124(2) | 0.013(0) | 0.005(3) | 0.012(1) | -0.126(2) | 0.013(0) |
| Seoul | 0.029 | 0.010 | -0.068 | 0.009 | 0.027(3) | 0.010(0) | -0.069(2) | 0.009(0) | 0.024(3) | 0.010(0) | -0.071(1) | 0.009(0) |
| Shanghai | 0.005 | 0.007 | -0.053 | 0.007 | 0.004(1) | 0.007(0) | -0.053(1) | 0.007(0) | 0.004(1) | 0.007(0) | -0.053(1) | 0.007(0) |
| Singapore | 0.006 | 0.008 | -0.112 | 0.008 | 0.003(2) | 0.007(0) | -0.115(1) | 0.008(0) | 0.002(3) | 0.007(0) | -0.116(1) | 0.008(0) |
| Tel Aviv | 0.002 | 0.012 | -0.104 | 0.012 | 0.001(2) | 0.012(0) | -0.109(2) | 0.012(0) | 0.001(3) | 0.013(0) | -0.109(3) | 0.012(0) |
| | ||||||||||||
| Athens | -0.047 | 0.009 | -0.063 | 0.010 | -0.048(3) | 0.009(0) | -0.065(2) | 0.010(0) | -0.047(4) | 0.009(0) | -0.065(3) | 0.010(0) |
| Auckland | -0.035 | 0.006 | -0.232 | 0.007 | -0.039(2) | 0.006(0) | -0.235(1) | 0.006(0) | -0.039(4) | 0.006(0) | -0.234(1) | 0.006(0) |
| Edinburgh | -0.046 | 0.006 | -0.194 | 0.007 | -0.047(2) | 0.006(0) | -0.198(1) | 0.007(0) | -0.048(2) | 0.006(0) | -0.198(2) | 0.007(0) |
| Karlsruhe | -0.021 | 0.009 | -0.180 | 0.008 | -0.026(3) | 0.008(0) | -0.183(1) | 0.008(0) | -0.032(5) | 0.008(0) | -0.183(2) | 0.008(0) |
| London | -0.036 | 0.002 | -0.191 | 0.003 | -0.036(1) | 0.002(0) | -0.193(0) | 0.003(0) | -0.040(2) | 0.002(0) | -0.192(1) | 0.003(0) |
| Mobile | -0.117 | 0.006 | -0.310 | 0.009 | -0.115(2) | 0.006(0) | -0.309(1) | 0.009(0) | -0.113(4) | 0.006(0) | -0.307(1) | 0.009(0) |
| Nairobi | -0.017 | 0.011 | -0.125 | 0.010 | -0.018(4) | 0.011(1) | -0.127(2) | 0.010(0) | -0.019(3) | 0.011(0) | -0.126(2) | 0.010(0) |
| Porto Alegre | -0.021 | 0.007 | -0.116 | 0.008 | -0.023(2) | 0.007(0) | -0.118(2) | 0.008(0) | -0.023(3) | 0.007(1) | -0.117(2) | 0.008(0) |
| Toronto | -0.012 | 0.004 | -0.130 | 0.005 | -0.012(1) | 0.004(0) | -0.131(1) | 0.005(0) | -0.014(2) | 0.004(0) | -0.130(1) | 0.005(0) |
| Yerevan | -0.035 | 0.013 | -0.147 | 0.013 | -0.036(3) | 0.013(0) | -0.150(2) | 0.013(0) | -0.044(5) | 0.012(0) | -0.151(2) | 0.013(0) |
由于OSM提供的初始数据较为粗糙,并不满足拓扑分析的要求,需要进行处理。处理的基本步骤为:(1) 检查数据的一致性,目的是排除重叠的道路;(2) 数据增强[27, 28],识别道路网中的复杂交叉点、复式双行路、立交桥、道路附属设施等模式;(3) 模式的典型化,对上述模式进行典型化处理,使之变成简单的图结构;(4) 道路网的拓扑检查,包括删除孤立道路和保持路网连通。
经过上述处理后生成道路网的Stroke。在道路网拓扑分析中通常采用道路同名法和EBF、SBF、SF三种策略生成Stroke[12, 13],当然,在道路网综合研究中还有考虑道路等级的生成方法[14]。同名法即将路名相同的道路连接在一起形成Stroke。由于道路名和等级信息经常缺失,所以本文暂时仅采用EBF、SBF和SF三种策略生成Stroke,连接角度根据经验值设为60°[29]。由于生成Stroke的结果不唯一,为了判断其是否对度相关性度量结果产生影响,所以需要生成多次,在本文实验中每种策略均生成20次。生成Stroke之后,根据其相交关系形成对偶图。该对偶图是基于Stroke的拓扑表达[1],图的节点对应于Stroke,图的边对应于Stroke的相交关系。
2 度相关性的度量
度量度相关性的方法主要分为两类:第一类计算由任一边连接的节点的相关性,如度为k的节点是否倾向于与度为k'的节点相连的条件概率[30], 任意一条边连接度为k和k′的联合分布概率[31],此类方法通常根据计算结果的图像来判断网络的度相关性;第二类计算所有网络边两端的节点度的相关系数,如应用广泛的Newman同配性系数[4]、克服超级节点影响的改进的Pearson同配性系数[32]、Litvak-Hofstad同配性系数[9]。相比第一类,第二类由于给定具体的值,更易于判断网络的度相关性。
Newman同配性系数是节点剩余度的Pearson相关系数,数值上等于节点度的Pearson相关系数[4],而Litvak-Hofstad同配性系数实质上是节点度的Spearman相关系数。Litvak-Hofstad同配性系数能揭示较强的异配性,在同一机制产生的网络上具有一致性,克服了Newman同配性系数易受网络尺寸影响的缺陷。本文选择Newman同配性系数和Litvak-Hofstad同配性系数度量道路网的度相关性,二者可以互相对比和验证。之所以未选择改进的 Pearson同配性系数,是因为Litvak-Hofstad同配性系数是计算节点间度的等级相关性,将度的绝对值转换为等级,所以即便是超级节点,也变成了等级高的节点;再者,即便连接形成Stroke,由于道路网是一类地理网络,受空间限制,网络中很难存在类似于互联网或人际关系网中的超级节点。
定义随机变量J和K是总边数为M的无向图中某边连接的两个节点的度。对边i,ji 和ki是边i的两端节点的度,Newman同配性系数计算公式为:
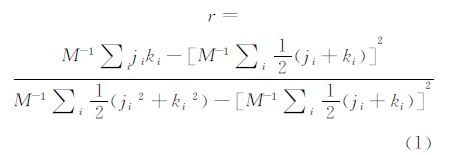
令tij和tik是边i两端节点度排序后的序,由于边两端的节点是无序的,故以1/2的概率随机记录两种可能的顺序之一[9],Litvak-Hofstad同配性系数计算公式为:
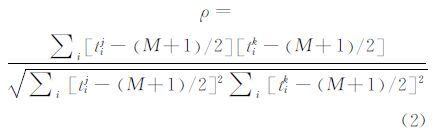
为了评价结果的显著性,有必要估计同配性系数的统计误差。不具有显著性的网络将被判定为零结果,即既不同配也不异配。根据文献[16],采用刀切法估计统计误差:
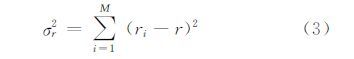
式中,ri和ρi分别是去掉第i边后的r和ρ值。
道路网在受到蓄意攻击时的鲁棒性,采用静态分析方法[2],即按度对节点(本文中指Stroke)降序排列,逐点删除后评价其对网络功能的破坏[2]。网络功能运用最大连通分量占比(G)和其余连通分量的平均节点数(<g>)度量。综合考虑文献[2, 6]的实际做法,采用两种方式进行评价。第一种方式是通过<g>的变化寻找网络崩溃的关键点,关键点对应的删除比例fc定义为网络鲁棒性的指标;第二种方式是定义G=0.5时的删除比例fG为描述网络鲁棒性的指标,显然fc和fG越大代表网络鲁棒性越强。
4 结果与讨论实验结果见表 1,表 1中列出了每种Stroke生成策略的20个Stroke集的同配性系数均值及其误差的均值,括号内的数字表示20次结果在最后一位小数上的不确定性,即标准差。如-0.048(2)表示-0.048±0.002。运用Newman同配性系数度量,37个路网异配,4个路网同配,6个路网零结果,另外还有3个路网的不同Stroke集结果不一致;而用Litvak-Hofstad同配性系数进行度量,46个路网异配,4个路网同配,没有出现零结果,不同Stroke集的度量结果具有一致性。两者均反映出绝大多数城市呈现异配性和不相关,而且呈现同配的城市,其同配性系数值很小(如Barcelona的Newman同配性系数最大值为0.055,其Litvak-Hofstad同配性系数最大值为0.082)。虽然所分析城市的幅度以及运用的分析方法不同,但是绝大多数城市道路网的度相关性呈现异配和不相关的结论与前人的研究结论相似[5, 6],说明城市道路网中度高的道路在局部范围内连接大量度低的道路。
两种同配性系数结果不一致的路网有8个(表 1中第4~11行),其中6个Newman同配性系数显示零结果而Litvak-Hofstad同配性系数结果为异配,1个路网前者为同配而后者为异配(Seoul),1个前者为异配而后者为同配(Curitiba)。另外,还有3个路网(表 1第1~3行),由于Newman同配性系数自身出现不一致的情况导致两种同配性系数无法比较。该结果与前人研究中提到的两者总是一致的结论[8]有差别。除New York、Terre Haute、Vancouver之外,同一个路网的Litvak-Hofstad同配性系数比Newman同配性系数的绝对值要大,验证了Litvak和Hofstad的结论,即Litvak-Hofstad同配性系数反应了强关系[9]。
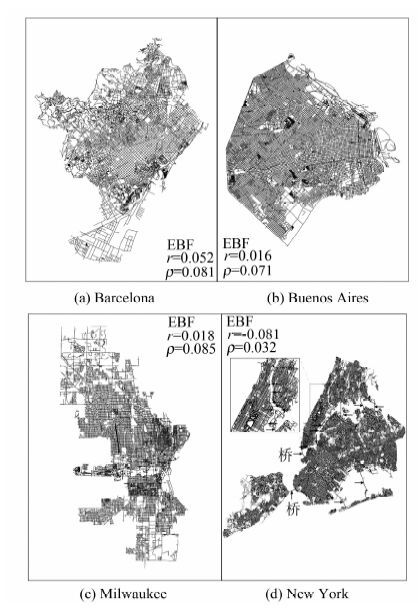
就形态特征而言,呈现同配的道路网的形态特征大致为存在大范围连接或全局性的网格模式,度相关性呈现异配的城市道路网没有固定的模式(见图 1),这在一定程度上说明几何模式与拓扑模式存在一定的联系。虽然呈现异配或不相关的道路网也存在大范围的网格模式,例如New York,但这些网格之间由桥相连。
|
| 图 1 4个大范围网格的城市道路网 Fig. 1 Four Urban Street Networks with Extensive Grid Pattern |
对每个城市道路网,关注由3种不同策略生成60次Stroke集之间的差别。本文实验中EBF策略产生的Stroke集是确定的(20次度量结果均相同),而SBF和SF生成的Stroke集不确定,通过对比同一城市的60次Stroke结果得到的同配性系数,发现不同Stroke集会对Newman同配性系数的度量产生影响,而对Litvak-Hofstad同配性系数的度量没有影响。在运用Newman同配性系数进行度量时,有3个城市(Bejaia、Osaka、Pittsburgh)出现了不一致的情况。产生不一致的原因可能在于Stroke生成本质上是组合问题,分支结构(如“Y”字形的路口)的选择会对某些路网的度量产生一定影响,然而网络本身作为一个复杂系统,具有一定的“容错性”,无论怎么连接,对结果的影响较小。总体而言,同一路网不同Stroke集对度相关性的度量影响较小。
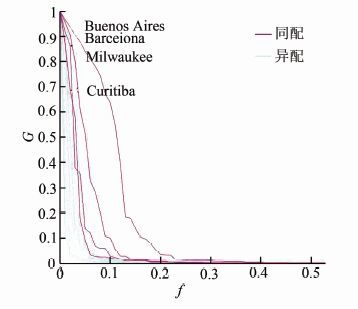
由于Newman同配性系数受不同Stroke集影响,暂时仅采用Litvak-Hofstad 同配性系数度量度相关性。从图 2中可以看出,同配网络的鲁棒性的确强于多数异配网络,但并不具有绝对性。该结果与Newman的结果有一定差异,其原因可能为:(1) Newman在保持了网络的节点数和度分布不变的情况下生成了不同同配性系数的网络,而本文所用的实际路网不满足节点数和度分布相同的条件,亦即可能存在别的原因影响网络的鲁棒性,如网络呈现无标度特性;(2) 虽然由Litvak-Hofstad同配性系数可将网络定性分为同配或者异配,但是,50个道路网的Litvak-Hofstad同配性系数的值相差并不大。就总体趋势而言,同配路网的鲁棒性强于异配网络,经过相关分析发现Litvak-Hofstad同配性系数鲁棒性指标fc和fG的Pearson相关系数分别为0.578和0.667,且在0.01显著性水平下具有统计显著性。这表明Litvak-Hofstad同配性系数与网络的鲁棒性存在正相关关系,这一点对于城市路网的规划具有一定的启示作用,对于自组织形成的异配路网可以通过适当的规划形成同配路网,以增强其鲁棒性。
|
| 图 2 50个城市道路网的鲁棒性 Fig. 2 Robustness of 50 Urban Street Networks |
本文运用Newman同配性系数和Litvak-Hofstad同配性系数对世界范围内的50个城市道路网的度相关性进行了分析,发现:(1) 以Stroke对偶法表示的城市道路网的度相关性绝大多数呈现异配和不相关,且Newman同配性系数和Litvak-Hofstad同配性系数会出现度量不一致的情况;(2) 同一路网的不同Stroke集对该路网的度相关性判断影响较小,在使用Litvak-Hofstad同配性系数度量时没有影响,在使用Newman同配性系数度量时会出现不一致的情况;(3) 运用Litvak-Hofstad同配性系数度量时,路网的度相关性与鲁棒性呈现正相关。
下一步的工作将在两个方面展开:第一,本文研究的数据来自世界范围,相对而言较为异质,具有一定的代表性,既有历史悠久的自组织型城市,也有新兴的规划型城市,那么绝大多数道路网的度相关性呈现异配并非偶然,其背后的路网形成与演化机制有待进一步研究;第二,除本文所用到的两种定量的度相关性度量方法之外,还有两种常用的定性度量方法,即平均最近邻度曲线和度相关性概况图,定量的度量方法能给出直观的数值,然而也会掩盖道路的真实连接关系,下一步的研究将结合定量与定性的度量方法进行更加全面的分析。
| [1] | Jiang Bin, Liu Chengke. Street-Based Topological Representations and Analyses for Predicting Traffic Flow in GIS[J]. International Journal of Geographical Information Science, 2009, 23(9):1119-1137 |
| [2] | Albert R, Jeong H, Barabasi A. Error and Attack Tolerance of Complex Networks[J]. Nature, 2000, 406:378-382 |
| [3] | Barabasi A, Albert R. Emergence of Scaling in Random Networks[J]. Science, 1999(286):509-512 |
| [4] | Newman M E J. Assortative Mixing in Networks[J].Physical Review Letters, 2002, 89(20):701-715 |
| [5] | Porta S, Crucitti P, Latora V. The Network Analysis of Urban Streets:A Dual Approach[J]. Physica A, 2006, 369:853-866 |
| [6] | Buhl J, Gautrais J, Reeves N,et al. Topological Patterns in Street Networks of Self-organized Urban Settlements[J]. The European Physical Journal B, 2006, 49(4):513-522 |
| [7] | Masucci A P, Smith D, Crooks A, et al. Random Planar Graphs and the London Street Network[J]. The European Physical Journal B, 2009, 71(2):259-271 |
| [8] | Tian Jing, Wu Dang, Zhan Yifei. Degree Correlation of Urban Street Networks[J]. Geomatics and Information Science of Wuhan University, 2014, 39(3):332-334(田晶, 吴荡, 湛逸飞. 城市道路网的度相关性研究[J]. 武汉大学学报·信息科学版, 2014, 39(3):332-334) |
| [9] | Litvak N, Hofstad R. Uncovering Disassortativity in Large Scale-Free Networks[J]. Physical Review E, 2013, 87:801-816 |
| [10] | Duan Yingying, Lu Feng. Robustness of City Road Networks at Different Granularities[J]. Physica A, 2014, 411:21-34 |
| [11] | Thomson R C, Richardson D E. The "Good Continuation" Principle of Perceptual Organization Applied to the Generalization of Road Networks[C]. The 19th International Cartographic Conference, Ottawa, 1999 |
| [12] | Jiang Bin. A Topological Pattern of Urban Street Networks:Universality and Peculiarity[J]. Physica A, 2007, 384:647-655 |
| [13] | Jiang Bin, Zhao Sijian, Yin Junjun. Self-organized Natural Roads for Predicting Traffic Flow:A Sensitivity Study[J]. Journal of Statistical Mechanics:Theory and Experiment, 2008(7):8-18 |
| [14] | Zhou Qi, Li Zhilin. A Comparative Study of Various Strategies to Concatenate Road Segment into Strokes for Map Generalization[J]. International Journal of Geographical Information Science, 2012, 26(4):691-715 |
| [15] | Crucitti P, Latora V, Marchiori M, et al. Error and Attack Tolerance of Complex Networks[J]. Physica A, 2004, 340:388-394 |
| [16] | Newman M E J. Mixing Patterns in Networks[J]. Physical Review E, 2003, 67(2):126-136 |
| [17] | Goodchild M F. Citizens as Sensors:The World of Volunteered Geography[J]. GeoJournal, 2007, 69:211-221 |
| [18] | Li Deren, Shao Zhenfeng. The New Era for Geo-information[J]. Science in China Series F:Information Sciences, 2009, 52(7):1233-1242 |
| [19] | Haklay M. How Good is Volunteered Geographical Information? A Comparative Study of OpenStreetMap and Ordnance Survey Datasets[J]. Environment and Planning B:Planning & Design, 2010, 4(37):682-703 |
| [20] | Girres J, Touya G. Quality Assessment of the French OpenStreetMap Dataset[J]. Transactions in GIS, 2010, 14(4):435-459 |
| [21] | Li Deren, Qian Xinlin. A Brief Introduction of Data Management for Volunteered Geographic Information[J]. Geomatic and Information Science of Wuhan University, 2010, 35(4):379-383(李德仁, 钱新林. 浅论自发地理信息的数据管理[J]. 武汉大学学报·信息科学版, 2010, 35(4):379-383) |
| [22] | Wang Ming, Li Qingquan, Hu Qingwu, et al. Quality Analysis on Crowd Sourcing Geographic Data with Open Street Map Data[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12):1490-1494(王明, 李清泉, 胡庆武,等. 面向众源开放街道地图空间数据的质量评价方法[J]. 武汉大学学报·信息科学版, 2013,38(12):1490-1494) |
| [23] | Jiang Bin, Liu Xintao. Scaling of Geographic Space from the Perspective of City and Field Blocks and Using Volunteered Geographic Information[J]. International Journal of Geographical Information Science,2011, 25(1):1-15 |
| [24] | Goetz M. Using Crowdsourced Indoor Geodata for the Creation of a Three-Dimensional in Door Routing Web Application[J]. Future Internet, 2012(4):575-591 |
| [25] | Hagenauer J, Helbich M. Mining Urban Land-Use Patterns from Volunteered Geographic Information by Means of Genetic Algorithms and Artificial Neural Networks[J]. International Journal of Geographical Information Science, 2012, 26(6):963-982 |
| [26] | Jiang Bin, Jia Tao.Zipf's Law for All the Natural Cities in the United States:A Geospatial Perspective[J]. International Journal of Geographical Information Science, 2011, 25(8):1269-1281 |
| [27] | Touya G. A Road Network Selection Process Based on Data Enrichment and Structure Detection[J]. Transactions in GIS, 2010, 14(5):595-614 |
| [28] | Yang Bisheng, Luan Xuecheng, Li Qingquan. Generating Hierarchical Strokes from Urban Street Networks Based on Spatial Pattern Recognition[J]. International Journal of Geographical Information Science, 2011, 25(12):2025-2050 |
| [29] | Jiang Bin. Street Hierarchies:A Minority of Streets Account for a Majority of Traffic Flow[J]. International Journal of Geographical Information Science, 2009, 23(8):1033-1048 |
| [30] | Boguná M, Pastor-Satorras R. Epidemic Spreading in Correlated Complex Networks[J]. Physical Review E, 2002, 66(4):104-114 |
| [31] | Maslov S, Sneppen K. Specificity and Stability in Topology of Protein Networks[J]. Science, 2002, 296(5569):910-913 |
| [32] | Xu Xiaoke, Zhang Jie, Sun Junfeng. Revising the Simple Measures of Assortativity in Complex Networks[J]. Physical Review E, 2009, 80:106-116 |
 2016, Vol. 41
2016, Vol. 41


