文章信息
- 武雪玲, 沈少青, 牛瑞卿
- WU Xueling, SHEN Shaoqing, NIU Ruiqing
- GIS支持下应用PSO-SVM模型预测滑坡易发性
- Landslide Susceptibility Prediction Using GIS and PSO-SVM
- 武汉大学学报·信息科学版, 2016, 41(5): 665-671
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 665-671
- http://dx.doi.org/10.13203/j.whugis20130566
-
文章历史
- 收稿日期: 2015-08-25

2. 国土资源部城市土地资源监测与仿真重点实验室, 广东深圳, 518034
2. Key Laboratory of Urban Land Resources Monitoring and Simulation, Ministry of Land and Resources, Shenzhen 518034, China
滑坡灾害易发性预测是滑坡监测、预警与评估的关键技术,是在现有滑坡灾害调查、编录的基础上,构建科学的预测模型,即依据滑坡灾害潜在区域内各种环境要素的空间分布,预测滑坡灾害的易发程度,为滑坡防灾减灾提供参考依据。三峡库区是我国重大地质灾害防治工作典型示范地区,滑坡灾害广泛发育且频繁发生,尤其自2008年11月首次172 m试验性高水位运行以来,每年汛期水位降至145 m,汛期过后再将水位升至175 m,致使145~175 m部分库岸周期性出没于水中,诱发滑坡地质灾害,严重威胁库区居民的生命财产安全[1, 2, 3]。因此,开展滑坡易发性定量分析研究,对滑坡防灾减灾具有重要意义。
滑坡灾害发育往往是复杂孕灾环境和多方诱发因素共同作用的结果,其易发性预测的前提是评价因子的科学提取。GIS因其强大的空间数据管理和分析功能,被作为滑坡易发性预测的支撑技术,遥感手段因具大范围、周期性重复观测能力而在滑坡灾害监测研究中被广泛关注[4]。目前,海量多时相遥感监测数据与非遥感数据的融合为区域范围内滑坡孕灾环境和诱发因素的信息提取提供了有效的数据支撑[5, 6]。滑坡易发性预测模型的选择直接影响滑坡易发性预测的效率和结果的可靠性,评价模型的适用性和准确性成为衡量其评价能力的重要标志。层次分析、信息量模型、逻辑回归等统计分析方法具有计算简单、性能稳定、分析结果易于解释等优点,被成功应用于大范围区域滑坡灾害研究[7, 8, 9]。确定性模型基于工程物理参数计算滑坡稳定性系数,结果的可靠性依赖于现场监测数据的详细程度,适用于小范围区域滑坡灾害研究。近年来,对地观测技术的迅速发展和新一代计算智能算法的提出,为挖掘滑坡与其孕灾环境和诱发因素之间的非线性关系提供了新思路。神经网络通过模仿人脑功能,对输入样本进行训练和学习、再学习,得到分析结果,被广泛用于滑坡易发性预测问题[10, 11]。支持向量机是继神经网络之后的新一代智能学习算法,它以结构风险最小原则取代传统机器学习方法中的经验风险最小化原则,具有很好的泛化能力,也已被用于滑坡易发性预测研究[12, 13, 14]。因此,本文以三峡库区长江干流岸坡作为研究对象,通过多源数据融合提取滑坡易发性预测因子,构建粒子群算法(particle swarm optimization,PSO)-支持向量机(support vector machine,SVM)模型,定量预测滑坡易发性。
1 PSO-SVMSVM是由Vapnik 1995年首次提出的继人工神经网络之后的新一代机器学习算法[15],它利用核函数将输入向量映射到一个高维特征空间,然后在特征空间中寻找分类最优超平面,实现对样本数据的分类。SVM参数的选择直接影响模型的预测精度,因此,寻求最佳模型参数(惩罚因子c和核参数σ)是模型选择的前提[16]。PSO是一种基于群体智能的全局优化计算方法,具有参数全局搜索能力强等优点,已被广泛应用于函数优化领域[17]。因此,本文选择具有较强非线性映射能力的径向基函数(radial basis function,RBF)作为SVM预测模型的核函数,利用PSO算法的全局寻优能力选择最优c和σ,构建滑坡易发性预测的PSO-SVM模型,主要步骤如下:
1) PSO-SVM模型初始参数设置,包括种群规模、迭代次数、学习因子、惯性权重、初始粒子和粒子初始速度。种群规模取值较小可提高运算速度但会降低种群的多样性,取值较大则会降低效率,通常取值为20~100。粒子向量代表一个SVM模型,该模型对应不同的c和σ。
2) 粒子寻优过程中,优化问题的每一个解都称为搜索空间中的一个粒子,根据适应度函数计算粒子适应值fi,适应度函数是选择个体的度量依据,粒子向量的c和σ对应一个SVM模型,进而对测试样本进行预测,个体优劣通过适应度函数来评价。
3) 根据目标函数,计算并比较每个粒子的适应值fi、种群个体最优解fi(pbest)和种群全局最优解fi(gbest)。如果fifi(pbest),则用新适应值替换前一轮的优化解,用新粒子替换前一轮的粒子,进而比较每个粒子的fi(pbest)和所有粒子的fi(gbest),如果fi(pbest)fi(gbest),则用每个粒子的最优解替换原所有粒子的最优解,同时保存粒子当前状态。
4) 判断适应值或迭代次数是否满足要求,如果种群中个体的适应值满足要求,或者达到终止进化代数,计算结束,该粒子个体对应最优c和σ组合,否则转至步骤2)继续进行迭代。
5) 将满足要求的全局最优粒子所对应的c和σ作为SVM最优参数组合,对训练样本进行训练,得到全局最优的PSO-SVM模型,定量预测滑坡易发性。
2 研究区概况及数据源 2.1 研究区概况研究区位于湖北省西部长江三峡库区秭归县郭家坝镇,距三峡大坝约35 km,地理坐标为东经110°42′~110°48′,北纬30°55′~30°58′,区域总面积65 km2,图 1为研究区地理位置示意图。该区为中低山和侵蚀峡谷地貌,相对高程达800~1 500 m。研究区受新构造运动的影响,山原期夷平面快速抬升,河流强烈下切,形成高陡岸坡,卸荷效应显著,滑坡、塌岸和崩塌等地质灾害广泛发育且频繁发生。滑坡是该区最为突出的地质灾害,具有分布广、数量多、发育机制复杂等特点。本文通过野外调查及辅助航片解译滑坡42处,总面积为3.29 km2,占区内地质灾害总数的90 %。
研究区地层岩性多样、构造复杂,易滑地层巴东组广泛分布,且大部分属于第四系堆积层滑坡,不仅提供了滑坡发育的物质条件,还控制空间孕灾环境的差异。褶皱和断裂是研究区的主要构造形式,褶皱发育有EW向的百福坪背斜和香龙山背斜、近SN向的秭归向斜和黄陵背斜,断裂主要有位于黄陵背斜西翼的仙女山断裂和九畹溪断裂。区内地层发育总体上自东向西渐新展布;香溪以东峡谷区震旦系至下三叠统地层连续出露,主要岩性为碳酸盐岩;香溪以西地区主要是中三叠系中统至侏罗系地层,主要岩性为砂岩、页岩、泥岩及灰岩、泥灰岩的地层岩性组合,为秭归盆地(秭归向斜)的物质组成,也是本区灾害发育地层组合。
2.2 数据源本文采用的主要数据源包括:① Landsat TM卫星影像1景(2010-05-02,轨道号为125/39)和我国环境减灾卫星影像HJ-1A 1景(2011-04-13,轨道号为7/76),用于提取土地利用、光谱和纹理特征因子、植被指数和湿度指数等地表覆盖信息;② 30 m分辨率的数字高程模型,主要用于提取地形地貌和水文特征等信息;③ 1∶50 000及1∶200 000数字化地质图,用于提取断层、斜坡结构和工程岩组等地质信息;④ 历史滑坡存档资料、野外调查资料及部分航片等,用于历史滑坡解译和空间定位。
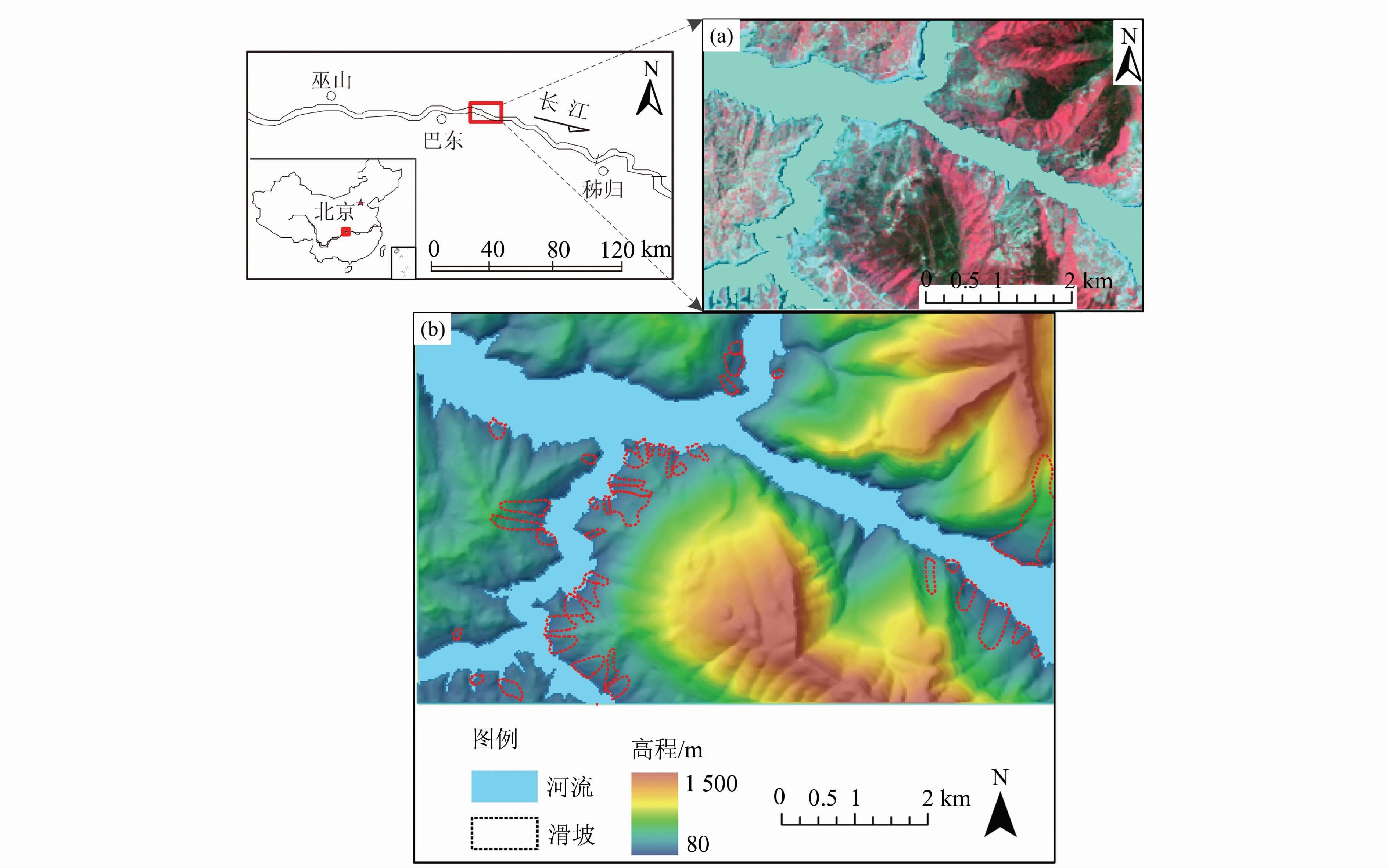
|
| 图 1 研究区地理位置示意图 Fig. 1 Location of the Study Area |
滑坡灾害的形成、演化和发生受时-空多源要素影响。根据研究区滑坡的具体特点和已有研究成果,本文提取四类评价因子:(1) 地形类因子:坡度和剖面曲率;(2) 地质类因子:工程岩组、断层距离和斜坡结构;(3) 光谱和纹理特征因子:同质性、第一和第二主成份;(4) 地表覆被及环境类因子:土地利用、库水影响和穗帽变换湿度指数(tasseled cap transformation wetness index,TCW)。为避免评价因子之间具有较强的相关性,采用Pearson积矩相关系数和显著性检验统计分析因子之间的相关程度和因子显著性(见表 1),相关系数绝对值小于0.68,重要性大于0.554,说明选取的11个评价因子具有相对独立性和重要性。表 1中,1为坡度,2为剖面曲率,3为工程岩组,4为同质性,5为第一主成份,6为第二主成份,7为斜坡结构,8为断层距离,9为土地利用,10为穗帽变换湿度指数,11为库水影响。进而统计分析研究区内历史滑坡与各评价因子之间的相关性,采用自然断点方法,将所有连续变量离散化为分类变量。本文滑坡易发性预测的初始决策表构建流程见图 2。
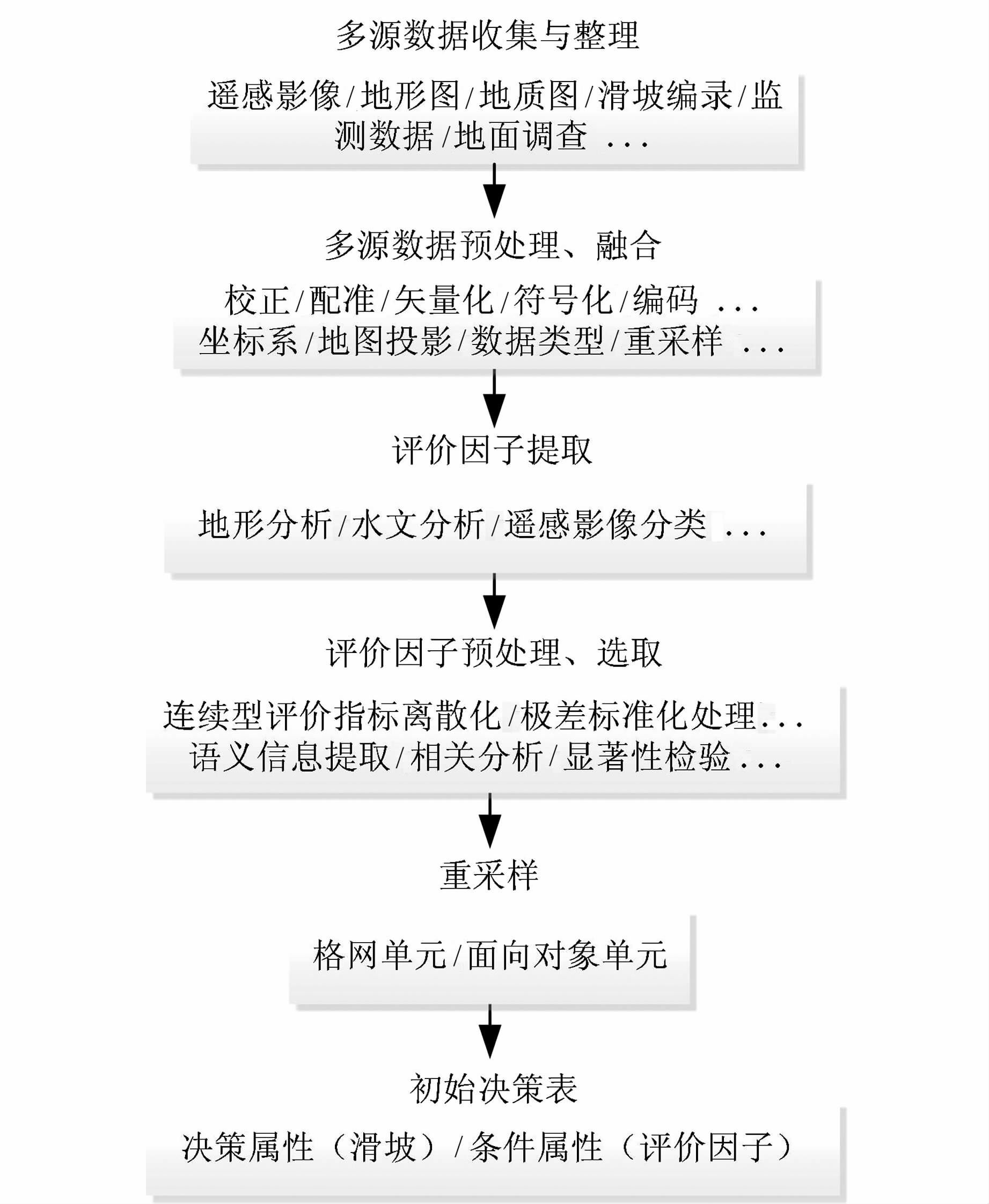
|
| 图 2 初始决策表构建流程图 Fig. 2 Flowchart of Generating Initial Decision Table |
模型单元是滑坡易发性预测的基本评价单元和绘图单元。格网模型单元对应于GIS中的栅格数据结构,采用矩阵形式存储数据网格单元便于数据采集、管理和计算,但其与地形地质等滑坡评价因子之间的相关性较差,容易产生冗余数据。因此,顾及重要专题数据,本文借鉴研究区的已有研究[18],通过Definiens Developer 8软件的多尺度分割功能,顾及重要专题数据,对Landsat TM影像进行分尺度分割,建立对象评价模型单元。为对比分析模型单元对滑坡易发性预测结果的影响同时通过栅格重采样,将研究区所有栅格单元大小统一为28.5 m × 28.5 m。最后,分别基于格网单元和对象单元对预测因子进行重采样,构成初始决策表,为滑坡易发性预测提供数据支撑。
3.2 PSO-SVM模型预测滑坡易发性从初始决策表中随机选取80%的滑坡和非滑坡数据形成训练样本集,其余20%作为测试样本[19]。设置PSO模型初始化参数,种群规模为20,最大迭代次数为100,学习因子c1和c2分别为1.5和1.7,惯性权重为0.6,搜索SVM惩罚因子c和核参数σ,得到最佳c=10.58,σ=0.23。利用最优组合参数,对训练样本进行学习,建立滑坡易发性与影响因素之间的非线性模型,进而将全部数据集输入模型,计算滑坡易发性指数(landslide susceptibility index,LSI),取值范围0~1,对应滑坡易发性从低到高。为了便于区分滑坡的易发程度,根据滑坡样本分布直方图特点,采用自然断点法将连续的滑坡易发性指数划分为5个滑坡易发性分区等级[20]:稳定区、低易发区、中易发区、高易发区和危险区(见图 3)。各分区所占总面积与滑坡分布比例见表 2,其中危险区和高易发区滑坡对象单元占整个研究区对象评价单元的87.69 %,危险区和高易发区滑坡对象单元占所有滑坡对象评价单元的13.40 %。从预测结果的总体空间分布形态来看,滑坡呈线状分布,主要分布于库水波动区和强影响区的长江干流及支流沿岸,高易发区主要分布在靠近秭归段长江干流沿岸、童庄河右岸和香溪河沿岸。
| 重要性 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 0.998 | 1 | |||||||||
| 2 | 0.994 | -0.16 | 1 | ||||||||
| 3 | 0.997 | 0.38 | -0.10 | 1 | |||||||
| 4 | 0.999 | -0.07 | 0.04 | -0.27 | 1 | ||||||
| 5 | 0.554 | -0.12 | 0.27 | 0.26 | -0.03 | 1 | |||||
| 6 | 0.995 | -0.56 | 0.19 | -0.36 | 0.24 | -0.04 | 1 | ||||
| 7 | 0.996 | -0.14 | 0.23 | 0.21 | -0.10 | 0.48 | -0.03 | 1 | |||
| 8 | 0.994 | -0.12 | 0.08 | -0.02 | 0.04 | -0.02 | 0.21 | -0.01 | 1 | ||
| 9 | 0.717 | -0.11 | 0.03 | 0.01 | 0.11 | -0.11 | 0.27 | 0.21 | 0.09 | 1 | |
| 10 | 0.663 | -0.17 | 0.32 | -0.10 | 0.02 | 0.60 | -0.21 | 0.27 | 0.14 | -0.17 | 1 |
| 11 | 0.999 | -0.43 | 0.21 | -0.62 | 0.37 | -0.13 | 0.68 | -0.08 | 0.26 | 0.07 | 0.08 |
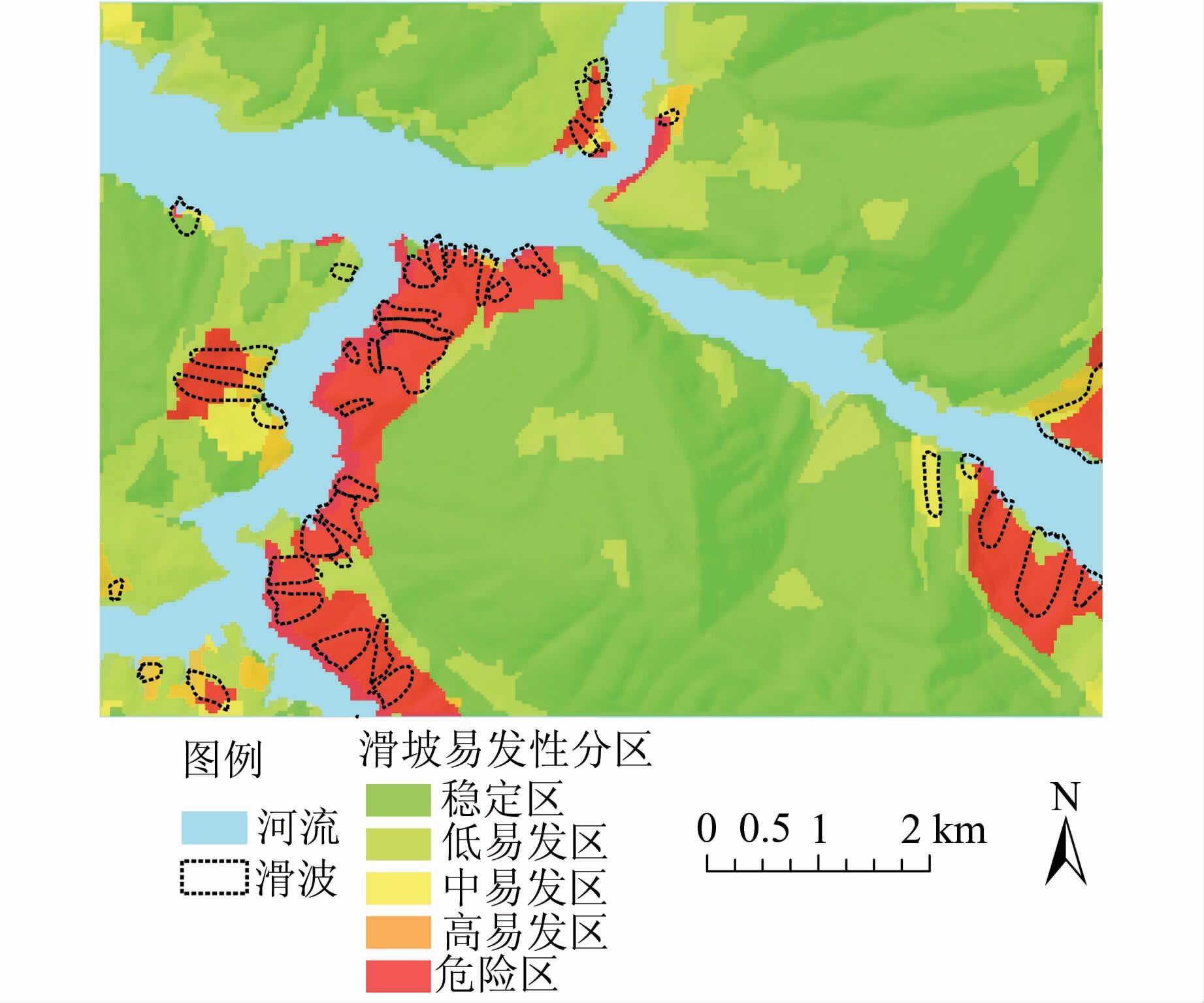
|
| 图 3 滑坡易发性分区图 Fig. 3 Landslide Susceptibility Zoning Map |
| 易发区等级 | 对象单元/% | 滑坡对象单元/% |
| 稳定区 | 57.18 | 1.24 |
| 低易发区 | 12.15 | 1.05 |
| 中易发区 | 17.27 | 10.02 |
| 高易发区 | 2.85 | 12.31 |
| 危险区 | 10.55 | 75.38 |
预测率曲线能定量衡量预测模型的准确度,取值范围为[0.5,1],曲线越陡,模型预测精度越高,曲线下面积为1表示一种理想状态,即模型预测结果与滑坡实际空间分布完全一致。为分析PSO-SVM模型的预测能力,本文根据测试样本数据集,通过比较滑坡易发性分区结果与已知滑坡的空间分布情况,绘制PSO-SVM模型的滑坡易发性指数-滑坡发生累计频率曲线(见图 4)。图 4中,横坐标表示LSI分级,共划分为100等分,按照1%累计减少,纵坐标表示各个LSI分级中滑坡发生的累积频率,曲线下面积(AUC)为0.841 5,即预测准确率为84.15 %。图 4中显示,对于92 %~100 %(横坐标8 %处)的预测指数,对应预测分区中的高易发区和危险区,能预测75.58 %的滑坡发生在高易发区和危险区;对于24 %~100 %(横坐标 76 %处)的预测指数,对应预测分区中的高易发区和危险区,能预测91.03 %的滑坡发生在高易发区和危险区。
此外,滑坡易发性预测的分类误差是一个成本问题,即“危险区”与“稳定区”的错分不等价。因此,定义I、II错误,I错误指将危险区划分为稳定区,II错误指将稳定区划分为危险区,则I错误率=I错误数/滑坡总数,II错误率=II错误数/非滑坡总数。PSO-SVM模型的分类预测结果见表 3,预测模型的总体正确率为90.51 %,I错误率为17.71 %。
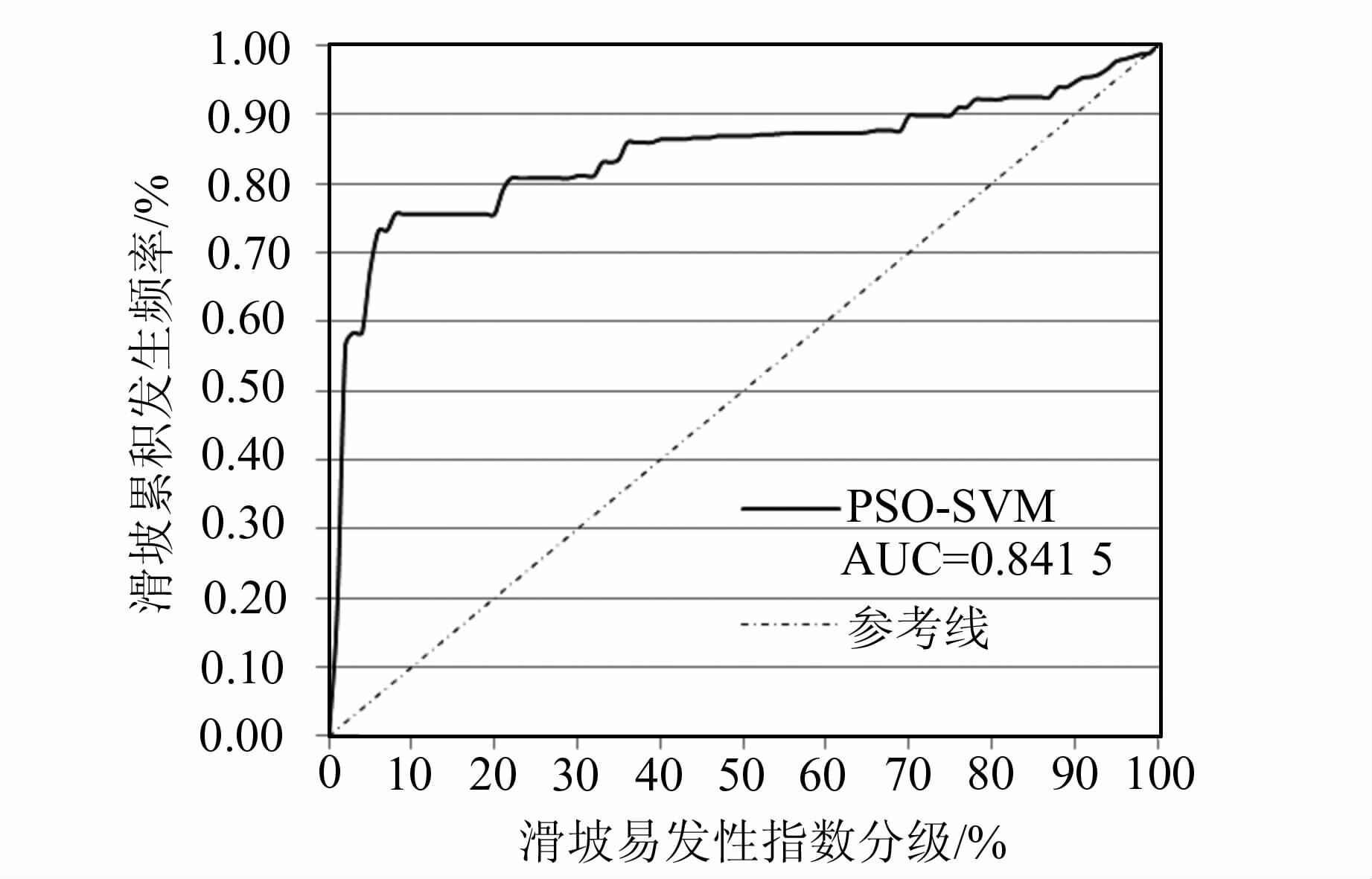
|
| 图 4 预测率曲线 Fig. 4 Prediction Rate Curve |
| 数据集 | 预测分类 | 合计 | 正确率/% | 错误率/% | ||
| 0 (稳定区) | 1 (滑坡) | |||||
| 实际分类 | 0(稳定) | 467 | 6 | 473 | 98.73 | 1.27 |
| 1(滑坡) | 17 | 79 | 96 | 82.29 | 17.71 | |
| 合计 | 484 | 85 | 569 | 90.51 | 9.49 | |
最后,为了评估多尺度分割对象单元支持下PSO-SVM滑坡易发性预测模型的分类精度,结合本文研究区地形地质资料的比例尺和卫星遥感影像的空间分辨率,将11个评价因子专题图层和1个历史滑坡图层重采样为28.5 m×28.5 m,构造基于格网评价单元的初始决策表,该表包含63 079行12列。对该二维表随机选取80 %的滑坡和非滑坡数据形成训练样本集,其余20 %作为检验样本。采用混淆矩阵,计算格网单元SVM、对象单元SVM和PSO-SVM模型的分类精度(见表 4),对象单元SVM分类预测的总体精度(95.43 %)、使用者精度(89.36 %)、生产者精度(93.87 %)和Kappa系数(0.828 6)均高于格网单元SVM对应的精度,而对象单元PSO-SVM模型的总体精度(95.96 %)、使用者精度(94.71 %)和Kappa系数(0.849 0)又高于对象单元SVM对应的精度。通过预测率曲线、分类误差率和分类精度分析发现,对象单元PSO-SVM滑坡预测模型具有预测能力强和预测效率高的特点。
| 预测模型 | 总体精度/% | 使用者精度/% | 生产者精度/% | Kappa系数 |
| 格网单元SVM | 96.16 | 76.26 | 85.91 | 0.604 9 |
| 对象单元SVM | 95.43 | 89.36 | 93.87 | 0.828 6 |
| 对象单元PSO-SVM | 95.96 | 94.71 | 90.51 | 0.849 0 |
基于多源空间数据、GIS和智能计算方法,本文开展了三峡库区滑坡易发性预测研究,提取了滑坡易发性预测因子,采用相关分析和显著性分析方法检验其重要性和独立性;构建PSO-SVM预测模型定量预测滑坡易发性,并对比分析了基于格网单元和对象单元的预测精度。通过本文研究,得到以下初步认识:① PSO算法的快速全局寻优功能可以优化SVM模型的惩罚因子c和RBF核参数σ。因此,在滑坡预测模型输入特征集合相同的条件下,PSO-SVM模型的预测精度高于SVM模型,预测结果的总体正确率和Kappa系数分别为90.51 %和0.849 0;② 模型单元是滑坡易发性预测的基本评价单元,在评价因子和预测模型相同的情况下,基于对象单元预测结果的使用者精度和生产者精度都远高于基于格网单元的预测结果,结果表明滑坡预测模型单元的划分应同时考虑地形、地质特征和其他重要外部动力因素。
滑坡灾害具有发育机制复杂和突发性强等特点,在后续研究中,还有很多问题需要深入研究。例如,挖掘更为重要的滑坡灾害控制要素,收集降雨和地震等重要滑坡诱发因子资料,探索更为优化的滑坡智能模型等。
| [1] | Chen Deji, Man Zuowu. The Research and Demonstration of Some Major Geological Problems of Three Gorges Project[J]. Engineering Sciences, 2011, 13(7):43-50(陈德基, 满作武. 三峡工程几个重大地质问题的研究与论证[J]. 中国工程科学, 2011, 13(7):43-50) |
| [2] | Zheng Shouren. Some Considerations on Trial Impoundment Operation of Three Gorges Project at 175 m Water Level[J]. Yangtze River, 2010, 41(8):1-4(郑守仁. 三峡工程试验性蓄水175 m水位运行的相关问题[J]. 人民长江, 2010, 41(8):1-4) |
| [3] | Huang S, Luo L. Stability Analysis and Results of the Landslide Monitoring Datum in the Three Gorges Reservoir Area[J]. Geomatics and Information Science of Wuhan University, 2014,39(3):367-372(黄声享, 罗力. 三峡库区滑坡监测基准的稳定性分析及结果[J]. 武汉大学学报·信息科学版, 2014,39(3):367-372) |
| [4] | He S W, Pan P, Dai L, et al. Application of Kernel-based Fisher Discriminant Analysis to Map Landslide Susceptibility in the Qinggan River Delta, Three Gorges, China[J]. Geomorphology, 2012, 171/172:30-41 |
| [5] | Niethammer U, James M R, Rothmund S, et al. UAV-based Remote Sensing of the Super-Sauze Landslide:Evaluation and results[J]. Eng Geol, 2012, 128:2-11 |
| [6] | Gong J H, Yue Y J, Zhu J, et al. Impacts of the Wenchuan Earthquake on the Chaping River Upstream Channel Change[J]. Int J Remote Sens, 2012, 33(12):3907-3929 |
| [7] | Pradhan B. Landslide Susceptibility Mapping of a Catchment Area Using Frequency Ratio, Fuzzy Logic and Multivariate Logistic Regression Approaches[J]. J Indian Soc Remote Sens, 2010,38(2):301-320 |
| [8] | Zare M, Pourghasemi H R, Vafakhah M, et al. Landslide Susceptibility Mapping at Vaz Watershed (Iran) Using an Artificial Neural Network Model:A Comparison Between Multilayer Perceptron (MLP) and Radial Basic Function (RBF) Algorithms[J]. Arab J Geosci, 2013, 6(8):2873-2888 |
| [9] | Bui D T, Lofman O, Revhaug I, et al. Landslide Susceptibility Analysis in the Hoa Binh Province of Vietnam Using Statistical Index and Logistic Regression[J]. Nat Hazards, 2011, 59:1413-1444 |
| [10] | Wu Xueling, Ren Fu, Niu Ruiqing. Spatial Intelligent Prediction of Landslide Hazard Based on Multi-source Data in Three Gorges Reservoir Area[J]. Geomatics and Information Science of Wuhan University, 2013,38(8):963-968(武雪玲, 任福, 牛瑞卿. 多源数据支持下的三峡库区滑坡灾害空间智能预测[J]. 武汉大学学报·信息科学版, 2013,38(8):963-968) |
| [11] | Pradhan B. A Comparative Study on the Predictive Ability of the Decision Tree, Support Vector Machine and Neuro-Fuzzy Models in Landslide Susceptibility Mapping Using GIS[J]. Comput Geosci, 2013, 51:350-365 |
| [12] | Wu Xueling, Ren Fu, Niu Ruiqing, et al. Landslide Spatial Prediction Based on Slope Units and Support Vector Machines[J]. Geomatics and Information Science of Wuhan University, 2013,38(12):1499-1503(武雪玲, 任福, 牛瑞卿, 等. 斜坡单元支持下的滑坡易发性评价支持向量机模型[J]. 武汉大学学报·信息科学版, 2013,38(12):1499-1503) |
| [13] | Xu C, Dai F C, Xu X W, et al. GIS-Based Support Vector Machine Modeling of Earthquake-Triggered Landslide Susceptibility in the Jianjiang River Watershed, China[J]. Geomorphology, 2012, 145:70-80 |
| [14] | Ballabio C, Sterlacchini S. Support Vector Machines for Landslide Susceptibility Mapping:The Staffora River Basin Case Study, Italy[J]. Math Geosci, 2012, 44:47-70 |
| [15] | Vapnik V. Nature of Statistical Learning Theory[M]. New York:Wiley, 1995 |
| [16] | Yao X,Tham L G, Dai F C. Landslide Susceptibility Mapping Based on Support Vector Machine:A Case Study on Natural Slopes of Hong Kong, China[J]. Geomorphology, 2008, 101:572-582 |
| [17] | Wu X, Ren F,Niu R. Landslide Susceptibility Assessment Using Object Mapping Units, Decision Tree, and Support Vector Machine Models in the Three Gorges of China[J]. Environ Earth Sci, 2014, 71:4725-4738 |
| [18] | Kennedy J,Eberhart R C. Particle Swarm Optimization[C]. IEEE Int Conf Neural Netw, New York, 1995 |
| [19] | Pradhan B, Lee S. Landslide Susceptibility Assessment and Factor Effect Analysis:Backpropagation Artificial Neural Networks and Their Comparison with Frequency Ratio and Bivariate Logistic Regression Modeling[J]. Environ Modell Softw, 2010, 25:747-759 |
| [20] | Nandi A. A Application of Logistic Regression Model for Slope Instability Prediction in Cuyahoga River Watershed, Ohio, USA[J]. Georisk, 2008, 2(1):16-27 |
 2016, Vol. 41
2016, Vol. 41



