文章信息
- 杨军, 林岩龙, 张瑞峰, 王小鹏
- YANG Jun, LIN Yanlong, ZHANG Ruifeng, WANG Xiaopeng
- 一种大规模点云k邻域快速搜索算法
- A Fast Algorithm for Finding k-nearest Neighbors of Large-Scale Scattered Point Cloud
- 武汉大学学报·信息科学版, 2016, 41(5): 656-664
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 656-664
- http://dx.doi.org/10.13203/j.whugis20140191
-
文章历史
- 收稿日期: 2015-01-31

三维采样数据的重建是逆向工程、虚拟现实等领域的重要研究内容。目前大多的三维测量数据都是散乱点云数据,这类数据之间没有明显的拓扑关系。在实际应用中,如果直接对其进行重建将会遇到难以克服的困难,一般情况下,先搜索散乱点云的k邻域建立模型的局部拓扑关系。k邻域的搜索效率直接影响模型的重建速度以及曲面光滑等后续处理,因此对其搜索算法进行研究具有重要的理论和实际价值。
k邻域搜索的基本思想是计算任一点到其余各点的欧氏距离,然后升序排序,前面的k个点即为此点的k邻域点。这种方法简单直观、易于实现,但其时间复杂度较高,在点云规模较小时,此算法能取得较好的结果。然而,随着扫描设备的发展以及建模精度的不断提高,点云数据的规模也不断增大,这种方法的耗时是惊人的。国内外学者对此问题提出了一些比较快速的搜索算法,这些算法大致分为三类:第一类方法是利用立方体栅格缩小点云的搜索范围。文献[1, 2]在点云分块后进行搜索,但是每个子块内边界点的k邻域需要搜索与其最近的26个子空间,浪费了较多的时间。文献[3]在文献[1]的基础上,推广了文献[4]中只能解决二维问题的搜索方法,提出了一种新的搜索算法,该算法利用子块扩张方法避免搜索相邻子空间,但是如果点云分布不均匀,可能会造成某个子空间内的采样点特别多,在进行k邻域搜索时会进行大量的浮点运算,降低了搜索效率。文献[5] 采用二次分块策略,利用多个小立方体栅格逐步缩小k邻域的搜索范围以提高搜索效率,不过该算法仍然存在分块不均匀问题,而且算法的稳定性不是很理想。文献[6]将点云进行微小分块,利用待搜索点的球半径和微小分块的边长确定k邻域候选点的范围,虽然算法预想每个子块内点数在2~5之间,但是由于模型的多样性和采样的不均匀性,实际和预想有一定差距。文献[7]中以待搜索点到所对应立方体栅格的6个面的距离为球体半径的取值范围,通过逐步增加球体半径扩大搜索范围来进行k邻域搜索,但是该算法不适合k值较大的情况,而且在边界处的立方体栅格内进行k邻域搜索时可能会对搜索范围进行不必要的扩大,造成搜索时间的浪费。第二类方法是利用树的层级结构对点云进行k邻域搜索[8, 9, 10, 11, 12],但是这些方法思想比较复杂,不易实现,而且若邻近点和待搜索点处于不同层时会造成搜索范围的扩大,降低搜索效率,同时,树结构的创建也具有一定的时间消耗。另外,此类方法不适合大规模点云的k邻域搜索。第三类方法是利用Voronoi图对数据集进行k邻域搜索[13, 14],不过在构建点集Voronoi图时需进行较多的浮点运算,计算量仍然较大。在这三类方法中,第一类方法搜索效率较高,在实际中得到较为广泛的应用。马骊溟等人提出了不同于上述三类方法的新算法,利用点云数据坐标点的三维坐标序号对点集进行邻域搜索[15],算法视角独特,但是利用三维坐标序号缩小k邻域的搜索范围具有一定的局限性,限制了算法的应用。杨军等人在文献[15]的基础上,利用自身小立方体有效解决了原文算法搜索结果可能不正确的问题,而且采用分块策略,降低了三维坐标的排序复杂度,缩小了算法的搜索范围,在很大程度上提高了算法的效率[16],但是文献[16]算法中仍没有解决分块不均匀情况下排序耗时多的问题,而且算法对子空间的扩充增量没有定量描述。
本文针对大规模散乱点云数据提出了一种新的k邻域快速搜索算法。首先,根据子空间内点云数目的上限对整个点云空间在坐标轴方向上自适应分块,避免子空间内存在过多的点。其次,以待搜索点到所对应子块的6个面的最小距离为边长生成一个小立方体,通过小立方体内点云数目的控制阈值动态改变小立方体的大小,逐步减少其内k邻域候选点的个数,并且以待搜索点到小立方体边界的最小距离作为搜索终止条件。这样,就可减少浮点运算,保证搜索结果的准确性。然后,若待搜索点的k邻域搜索不成功,且小立方体没有超出子空间边界,则根据循环次数和边长增量的调节因子逐步扩大小立方体并重新搜索。最后,以搜索不成功的点到子空间边界的最小距离所对应的面的外法向量方向作为扩展方向,并以此面附近的所有搜索不成功的点到此面的最小距离的最大值作为该方向的扩展步长,对当前子空间有选择地定量扩展。
1 算法原理 1.1 小立方体定义对任一待搜索点p(px,py,pz),以p为中心、一定步长L为边长生成一个小立方体,此立方体称为待搜索点p的自身小立方体,其内的采样点满足:
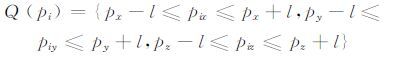
式中,l=L/2,即为边长的一半;(pix,piy,piz)为点pi的三维坐标。这些采样点称为p的k邻域候选点。
对任意点的自身小立方体而言,其6个面上朝向立方体内部的法向量称为此面的内法向量,朝向立方体外部的法向量称为此面的外法向量。其中,小立方体6个面的内外法向量方向和相应的坐标轴方向平行。
1.2 算法描述 1.2.1 点云空间的自适应分块首先计算整个点云空间的边界[xmin,xmax]、[ymin,ymax]、[zmin,zmax],将其作为初始子空间6个面的坐标值。根据设定的子空间内点云数目上限count值对初始子空间分块,若初始子空间内点云数目大于count,则按照如下规则对初始子空间分块:如果|xmax-xmin|最大,则在x方向将子空间平分,更新子空间6个面的坐标值;如果|ymax-ymin|最大,则在y方向将子空间平分,更新子空间6个面的坐标值;如果|zmax-zmin|最大,则在z方向将子空间平分,更新子空间6个面的坐标值。依此类推,直至所有子空间内的采样点数目小于count。其中,xmax、xmin,ymax、ymin,zmax、zmin分别为点云空间中在x方向、y方向、z方向上的最大值和最小值,count是设定的子空间内点云数目的上限值,|·|表示两个数值的绝对值。
1.2.2 k邻域快速搜索算法在完成点云空间自适应分块后,对子空间S内任一采样点p,按以下步骤对其进行k邻域搜索:
1) 若S内点云数目小于整个点集内点云数目,则以p到子空间6个面(非整个点云空间边界)的最小距离为边长生成初始自身小立方体;若S内点云数目等于总的点数,则以|xmax-xmin|、|ymax-ymin|、|zmax-zmin|中的最小值为边长生成初始自身小立方体。
2) 如果小立方体内点云数目在控制阈值之内,则按传统算法进行k邻域搜索;如果不在控制阈值之内,则以一定的步长增量,根据程序循环次数和边长增量调节因子动态改变小立方体大小,直至点云数目满足要求。这相当于得到一个大小动态变化的立方体,大小根据其内的采样点数目扩大或缩小,从而尽可能地缩小k邻域的搜索范围,提高算法效率。
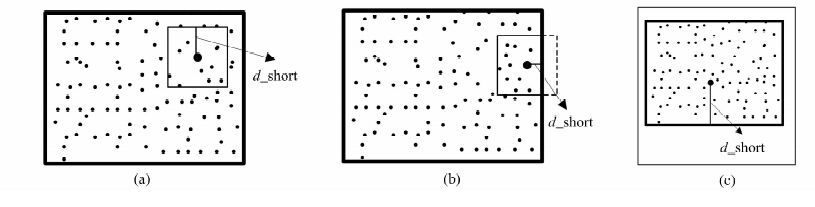
3) 计算最小距离d_short。若p到k个邻近点的欧氏距离不大于d_short,则p的k邻域搜索成功,令标示符flag=true,否则flag=false。如果p搜索不成功,且其自身小立方体没有超出子空间边界,如图 1(a)所示,或者p的自身小立方体部分超出子空间边界,并且这些边界恰好都是整个点云空间的边界,则以一定增量扩大其自身小立方体并重新搜索,d_short等于p到其自身小立方体边界的最小距离;若小立方体部分超出子空间边界,而这些边界不都是整个点云空间的边界,或者其完全超出子空间边界,如图 1(b)和1(c)所示,则不扩大其自身小立方体,程序退出,进行下一个点的k邻域搜索,此时,d_short等于p到子空间6个面(非点云空间边界)的最小距离。
|
| 图 1 d_short的计算方法 Fig. 1 Calculation Method of the d_short |
在图 (1)中,大圆黑点表示待搜索点p,粗线框表示子空间S边界,细线框表示p的自身小立方体的边界,虚线框为小立方体超出子空间边界的部分。
4) 若S内不存在搜索不成功的点,则S搜索完成,进入下一子空间搜索;若存在搜索不成功的点,则对子空间有方向性地进行扩充,然后按步骤1)~3)对搜索不成功的点重新搜索,直至搜索成功。
扩展方向选择规则:遍历S内搜索不成功的点,计算它们到子空间边界(非点云空间边界)的最小距离所对应的面,这些面的外法向量方向即为扩展方向,如图 2所示。
扩展步长计算规则:遍历S内搜索不成功的点,选择它们到子空间边界(非点云空间外壁)的最小距离的最大值作为扩展步长,在扩展方向上进行定量扩充。
点云空间k邻域快速搜索算法的详细步骤如下。
1) 以count为子空间点云上限,对点云空间进行自适应分块。
2) 对子空间S内任一点p生成p的初始自身小立方体,计算其内的点云数目K。如果K ≥ αk,且K≤ βk,则转入4),否则转入3)。其中,αk、βk为初始小立方体内k邻域候选点数目的控制阈值,α和β为控制阈值的左右调节因子。
3) 如果K<αk,则以 2(l + l×(b×m))为边长重新计算小立方体Q和点数K,并以l + l×(b×m)更新l值;如果K>βk,则以2(l-l×b)为边长重新计算Q和点数K,并以l-l×b更新l值。如果K>βk的循环次数超过其设定的上限,则β值加1,避免进入死循环。若K符合条件,则转入4),否则转到3)继续执行,直至满足要求。其中,l为当前小立方体边长的一半,m表示搜索满足控制阈值的小立方体Q时程序的循环次数,b为小立方体边长增量的调节因子,取值范围为(0,1)。
4) 计算相应的d_short。
5) 计算p到Q内k邻域候选点的欧氏距离并按升序排序。若前k个值不大于d_short,则认为p搜索成功,令flag=true,否则flag=false。若flag=false,且Q边界没有超出子空间S,如图 1(a)所示,则以2(l+(nc×b) ×l)为边长重新计算小立方体Q,并以l+(nc×b) ×l更新l值,按4)至5)在S内重新搜索p的k邻域,直至Q的边界部分超出子空间边界,且这些边界不都是点云空间边界,或者完全超出子空间的边界范围,如图 1(b)和图 1(c)所示,则不扩大p的小立方体,程序退出,进行子空间下一个点的k邻域搜索。其中,nc表示4)~5)的循环次数。
6) 若空间内所有点搜索成功,则进入下一子空间搜索;若搜索不成功,则按扩展方法对S进行扩展,按2)~5)重新对搜索不成功的点进行搜索,直至这些点搜索成功。
7) 对整个点云空间内所有子空间进行k邻域搜索。
8) 结束。
2 实验结果与分析实验中,点云数据均为真实物体的三维扫描数据,如图 2,图 3,图 4所示,图中小括号内的数字表示点云模型的数据量,例如,图 2(a)中“3 233 点”表示该点模型共包含3 233个点。所有实验均在联想X200型个人笔记本电脑(酷睿双核,内存2G,主频2.4 GHZ)上完成,测量时间为1个采样点正确完成k邻域搜索的平均CPU时间,单位为ms。
2.1 实验1实验1研究不同的count值对算法搜索效率的影响。实验结果如表 1所示,测量的分块时间为每个点的平均时间,实验模型如图 2(a),图 2(b),图 2(c),实验数据在a=1,β=3,b=0.2的情况下测得。由表 1中实验数据可以看出,对同一模型,随着count值的改变分块时间变化不大;对不同模型,分块时间有所改变,说明算法的分块效率受模型的采样密度影响。对同一模型,count较小时(如count=50),k邻域的搜索耗时较大,因为此时子空间内点数比较少,在搜索过程中可能需要对子空间多次扩展。随着模型规模增大,搜索时间也将有所增大,因为模型规模较大时子空间数目增多,对子空间扩展的总次数也随之增大,耗时增多,而且随着k的增大搜索时间逐步增加。如果count值过大,对k邻域的搜索时间也会增加,这是因为子空间内点云数目较多。如果待搜索点初始自身小立方体内的k邻域候选点数目不满足要求,为了使其点数满足要求,需要对自身小立方体边长进行动态改变,这样每次改变时需要遍历的点数和次数过多,造成了一定的时间浪费。
通过实验1,取count=500进行实验2,分析控制阈值的左右调节因子对算法搜索效率的影响。
| 模型 | 测试时间 | count | |||||||||
| 50 | 100 | 300 | 500 | 1 000 | 1 500 | 2 000 | 2 500 | 3 000 | 4 000 | ||
| 图 2(a) | |||||||||||
| 分块时间 | 0.073 | 0.072 | 0.072 | 0.070 | 0.070 | 0.069 | 0.069 | 0.068 | 0.067 | 0.065 | |
| k=10 | 0.097 | 0.080 | 0.093 | 0.091 | 0.117 | 0.134 | 0.158 | 0.155 | 0.299 | 0.236 | |
| k=50 | 0.236 | 0.226 | 0.245 | 0.245 | 0.246 | 0.265 | 0.265 | 0.274 | 0.328 | 0.231 | |
| k=100 | 0.381 | 0.376 | 0.448 | 0.434 | 0.419 | 0.420 | 0.265 | 0.274 | 0.328 | 0.511 | |
| 图 2(b) | |||||||||||
| 分块时间 | 0.082 | 0.070 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.065 | 0.065 | 0.065 | |
| k=10 | 0.133 | 0.083 | 0.065 | 0.073 | 0.098 | 0.114 | 0.203 | 0.155 | 0.210 | 0.416 | |
| k=50 | 0.279 | 0.225 | 0.185 | 0.194 | 0.227 | 0.265 | 0.245 | 0.266 | 0.283 | 0.487 | |
| k=100 | 0.420 | 0.363 | 0.341 | 0.342 | 0.373 | 0.400 | 0.383 | 0.398 | 0.348 | 0.487 | |
| 图 2(c) | |||||||||||
| 分块时间 | 0.113 | 0.079 | 0.078 | 0.077 | 0.077 | 0.077 | 0.076 | 0.076 | 0.076 | 0.076 | |
| k=10 | 0.661 | 0.459 | 0.327 | 0.312 | 0.323 | 0.394 | 0.419 | 0.441 | 0.491 | 0.498 | |
| k=50 | 0.420 | 0.363 | 0.341 | 0.342 | 0.373 | 0.400 | 0.383 | 0.398 | 0.324 | 0.487 | |
| k=100 | 1.822 | 0.625 | 0.513 | 0.486 | 0.495 | 0.570 | 0.596 | 0.625 | 0.680 | 0.680 | |
实验数据为k邻域搜索时间,不包含模型的分块时间,其中实验数据在b=0.2的情况下测得,结果如表 2所示,实验模型如图 2(a)、图 2(c)。对同一模形,相同β和k,a较小时k邻域搜索效率较高,a过大时搜索效率较低,这是因为在a过大时小立方体内包含过多的k邻域候选点,在搜索时进行较多的浮点运算,这样造成时间的浪费,而且随着k的增大时间差距逐步增加;对同一模型,取相同的k、a值,不同的β值时,在k值比较小时算法搜索时间相差微小,随着k的增大差距有所增加,这是因为随着k的增加,自身小立方体的左右两侧控制阈值都有所增加,使其内的候选点数目增加,进行了较多的运算。由表 2中数据可以看出,同一模型,相同k时,算法在不同的β和a值下搜索时间变化不大,相对比较稳定。
通过实验1和实验2,取count=500,a=1,β=3进行实验3和实验4,分析研究边长调节因子b对算法效率的影响。
2.3 实验3实验数据为k邻域搜索时间,不包含模型的分块时间,结果如表 3所示,实验模型如图 2(a),图 2(b),2(c)。由表 3中数据可以看出,对同一模型,取相同的k值、不同的b值时,在k和模型规模较小时邻域搜索时间相差不大,但随着k和点云模型数据增多,时间的变化幅度也逐步增大。对同一模型,取相同的b值、不同的k值时,随着k值的增加其搜索时间逐步增大,但是随着模型规模的增大时间变化幅度并没有明显的改变,说明算法对模型和b值都有较强的稳定性,而且b值一般集中在0.2~0.4之间。
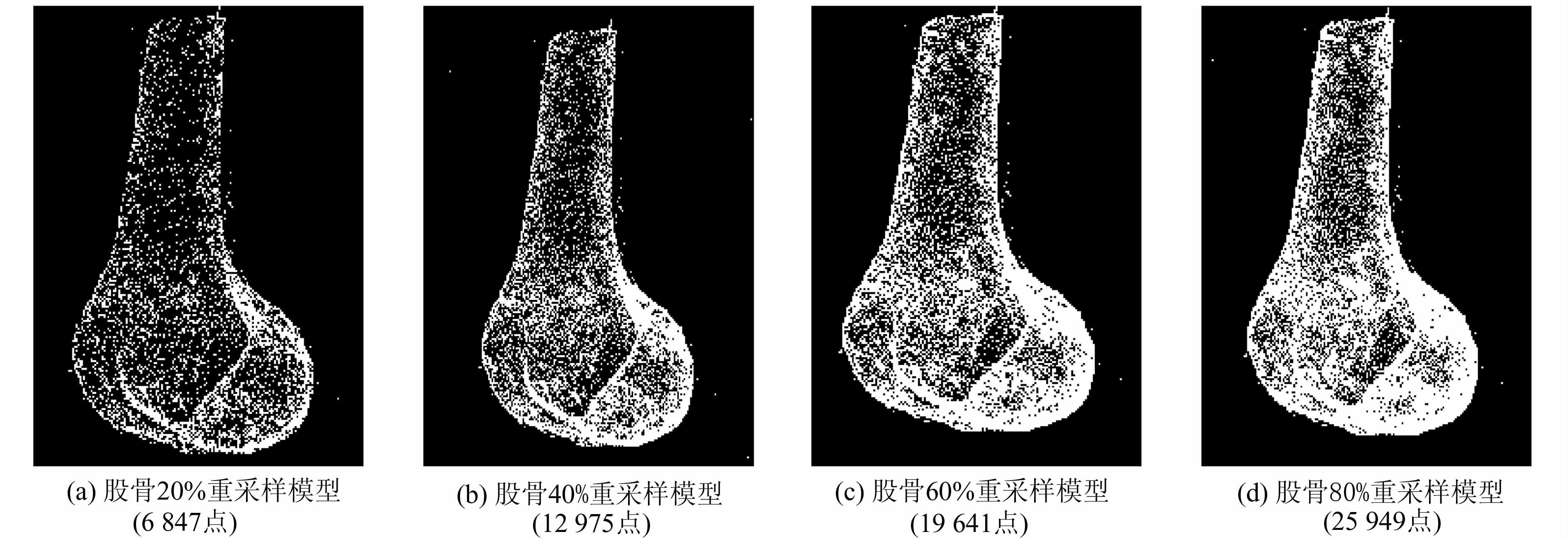
2.4 实验4实验4研究同一拓扑结构的不同采样密度对本算法的影响,实验数据为k邻域搜索时间,不包含模型的分块时间,结果如表 4所示,实验模型为图 2(d)、3(a),3(b),3(c),3(d)。由表 4中数据可以看出,b的分布和实验3的分析结果相同,都集中在0.2~0.4之间,说明b对模型的采样密度具有较强的稳定性。在模型采样密度较小时,取相同的k值、不同的b时,k邻域的搜索时间相差不大,但随着k值的增大时间差距逐渐变大。对不同采样密度,取相同的k值时,随着采样密度的增大搜索时间逐步增加,但是幅度不大,说明算法对b值有一定稳定性。由表 4中数据可知,b值过大或过小时都会造成搜索时间的增加,这是因为当自身小立方体内的点云数目不满足要求时,对自身小立方体边长的改变幅度过大或过小,需要多次的循环操作才能使其内的点数满足要求,这样就造成了一定的时间浪费。不过,由于b分布的规律性,在实际应用中取b=0.2即可得到模型k邻域搜索的最佳或接近最佳速率。

|
| 图 2 膝关节点云模型 Fig. 2 Point Cloud Models of Knee Joint |
|
| 图 3 膝关节股骨重采样模型 Fig. 3 Resampled Femur Models of Knee Joint |

|
| 图 4 常用的点云模型 Fig. 4 Common Point Cloud Models |
通过上述实验,取count=500,a=1,β=3,b=0.2进行实验5,对不同算法的效率进行研究。
| 模型 | k | β=3 | β=5 | β=7 | |||||
| a=1 | a=2 | a=1 | a=2 | a=3 | a=1 | a=2 | a=3 | ||
| 10 | 0.091 | 0.096 | 0.087 | 0.101 | 0.105 | 0.089 | 0.095 | 0.111 | |
| 图 2(a) | 50 | 0.246 | 0.261 | 0.241 | 0.284 | 0.327 | 0.259 | 0.395 | 0.356 |
| 100 | 0.405 | 0.458 | 0.434 | 0.497 | 0.545 | 0.448 | 0.512 | 0.569 | |
| 10 | 0.114 | 0.128 | 0.110 | 0.120 | 0.136 | 0.109 | 0.119 | 0.134 | |
| 图 2(c) | 50 | 0.312 | 0.351 | 0.317 | 0.360 | 0.426 | 0.316 | 0.363 | 0.436 |
| 100 | 0.486 | 0.569 | 0.511 | 0.598 | 0.711 | 0.522 | 0.613 | 0.730 | |
| 模型 | k | b | ||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| 图 2(a) | 10 | 0.116 | 0.091 | 0.087 | 0.084 | 0.426 | 0.316 | 0.363 | 0.436 | 0.115 |
| 50 | 0.280 | 0.246 | 0.232 | 0.233 | 0.246 | 0.245 | 0.299 | 0.285 | 0.318 | |
| 100 | 0.280 | 0.246 | 0.232 | 0.233 | 0.246 | 0.245 | 0.299 | 0.5175 | 0.521 | |
| 图 2(b) | 10 | 0.085 | 0.073 | 0.067 | 0.067 | 0.071 | 0.073 | 0.090 | 0.092 | 0.091 |
| 50 | 0.223 | 0.194 | 0.185 | 0.190 | 0.209 | 0.204 | 0.250 | 0.242 | 0.258 | |
| 100 | 0.379 | 0.342 | 0.335 | 0.348 | 0.373 | 0.370 | 0.448 | 0.423 | 0.452 | |
| 图 2(c) | 10 | 0.131 | 0.114 | 0.111 | 0.110 | 0.122 | 0.132 | 0.150 | 0.150 | 0.149 |
| 50 | 0.337 | 0.312 | 0.319 | 0.329 | 0.2376 | 0.408 | 0.456 | 0.557 | 0.521 | |
| 100 | 0.529 | 0.486 | 0.515 | 0.530 | 0.577 | 0.625 | 0.714 | 0.731 | 0.771 | |
| 注:表中下划线表示b值对于不同k的最佳搜索效率。 | ||||||||||
| 模型 | k | b | ||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| 图 3(a) | 10 | 0.107 | 0.088 | 0.083 | 0.084 | 0.426 | 0.316 | 0.363 | 0.436 | 0.115 |
| 50 | 0.273 | 0.233 | 0.223 | 0.233 | 0.246 | 0.245 | 0.299 | 0.285 | 0.316 | |
| 100 | 0.540 | 0.419 | 0.416 | 0.233 | 0.246 | 0.245 | 0.299 | 0.5175 | 0.568 | |
| 图 3(b) | 10 | 0.108 | 0.0113 | 0.101 | 0.067 | 0.071 | 0.073 | 0.090 | 0.092 | 0.136 |
| 50 | 0.493 | 0.454 | 0.451 | 0.190 | 0.209 | 0.204 | 0.250 | 0.242 | 0.350 | |
| 100 | 0.493 | 0.454 | 0.451 | 0.348 | 0.373 | 0.370 | 0.448 | 0.423 | 0.627 | |
| 图 3(c) | 10 | 0.131 | 0.116 | 0.111 | 0.110 | 0.122 | 0.132 | 0.150 | 0.150 | 0.149 |
| 50 | 0.337 | 0.312 | 0.263 | 0.329 | 0.2376 | 0.408 | 0.456 | 0.557 | 0.521 | |
| 100 | 0.529 | 0.457 | 0.515 | 0.530 | 0.577 | 0.625 | 0.714 | 0.731 | 0.771 | |
| 图 3(d) | 10 | 0.131 | 0.116 | 0.111 | 0.119 | 0.122 | 0.132 | 0.150 | 0.150 | 0.149 |
| 50 | 0.337 | 0.276 | 0.263 | 0.329 | 0.2376 | 0.408 | 0.456 | 0.557 | 0.521 | |
| 100 | 0.529 | 0.468 | 0.515 | 0.530 | 0.577 | 0.625 | 0.714 | 0.731 | 0.771 | |
| 图 2(d) | 10 | 0.131 | 0.116 | 0.111 | 0.133 | 0.122 | 0.132 | 0.150 | 0.150 | 0.149 |
| 50 | 0.337 | 0.299 | 0.263 | 0.329 | 0.2376 | 0.408 | 0.456 | 0.557 | 0.521 | |
| 100 | 0.529 | 0.486 | 0.515 | 0.530 | 0.577 | 0.625 | 0.714 | 0.731 | 0.771 | |
| 注:表中下划线表示b值对于不同k的最佳搜索效率。 | ||||||||||
实验5结果见表 5,实验模型为图 2(a),图 2(b),图 2(c),图 2(d),图 4(a),图 4(b),图 4(c),图 4(d),图 4(e),图 4(f)。由表 5中数据可知,本文算法的搜索效率明显高于文献[5]算法和文献[3]算法,随着模型和k值的增大,优势更加明显。对于不同模型,同一k值,本文算法随着模型数据量增大搜索时间略有增加,而其他两种算法,增加的幅度明显大于本文算法。这是因为文献[3]根据一定的步长对点云分块,然后对每个子块内采样点进行搜索,如果子块内点云数目较多,每次搜索时都要进行较多的浮点计算,这在很大程度上降低了搜索效率,而且,在子块内每个采样点搜索不成功时,都需要子空间向四周扩展,这又造成了时间的消耗,而且算法并没有对扩展步长进行自适应计算。文献[5]算法利用不同的子空间结构缩小k邻域候选点的搜索范围,然后利用球空间进行k邻域搜索,如果采样点密度较高可能会造成球空间内点云数目过大,需进行大量的数值计算,而且几乎每一个点的邻域搜索都要进行球空间的计算,这是造成文献[5]算法搜索速度偏低的主要原因。相反,本文算法首先利用count值在坐标方向对点集自适应分块,尽量避免子空间内点云数目过多,不用考虑模型的采样密度;然后利用自身小立方体点数的控制阈值进一步缩小k邻域的搜索范围,这在很大程度上提高了算法的搜索速度;其次,当子空间内存在搜索不成功的点时,对其进行有选择地定量扩展,对其内所有的搜索不成功点遍历搜索,而不是每一个搜索不成功点都进行扩展空间重新计算,这进一步提高了算法速度,并提高了算法的自适应程度;最后,本文算法利用搜索不成功点到子空间6个面(非整个点云空间边界)的最小距离的最大值作为扩展方向的扩展步长,这不仅考虑了待搜索点的局部密度,而且对扩展步长自适应计算,尽量减少子空间额外扩展次数,提高算法速度。同时,本文算法只是在模型第一次k邻域搜索时才进行分块,这进一步提高了算法的k邻域搜索效率,而文献[3]和文献[5]算法每次进行k邻域搜索都要进行分块,比较浪费时间。另外,文献[5]算法出现模型数据规模小而搜索效率反而更慢的现象,如表 5中模型Femur的搜索,并且对同一模型,频繁出现k值大时反而搜索更快的现象,如表 5中Femur、Victoria、Micahael等多个模型的搜索,出现这种现象的原因是该算法的搜索效率主要取决于Ssphere的计算,而Ssphere的计算与分块结果以及模型的局部采样密度密切相关,然而模型的分块结果和k值相关。同时,文献[5]算法并没有充分考虑模型的局部采样密度,这可能是导致出现这种现象的另一个原因。
| 算法 | k | ACL | Patella | Cat | Mannequin | Teapot | Tibia | Femur | Bunny | Victoria | Micahael |
| 本文算法 | 10 | 0.161 | 0.140 | 0.140 | 0.144 | 0.169 | 0.188 | 0.192 | 0.165 | 0.189 | 0.521 |
| 50 | 0.256 | 0.567 | 0.154 | 0.143 | 0.169 | 0.129 | 0.188 | 0.55 | 0.124 | 0.135 | |
| 100 | 0.405 | 0.34 | 0.143 | 0.116 | 0.86 | 0.56 | 0.142 | 0.143 | 0.35 | 0.451 | |
| 文献[3] 算法 | 10 | 0.235 | 0.140 | 0.140 | 0.356 | 0.169 | 0.687 | 0.192 | 0.165 | 0.143 | 0.169 |
| 50 | 0.222 | 4.567 | 4.112 | 0.143 | 2.187 | 1.188 | 0.55 | 0.123 | 0.135 | 0.534 | |
| 100 | 0.567 | 4.34 | 2.143 | 0.134 | 0.876 | 4.55 | 4.121 | 1.132 | 0.35 | 0.451 | |
| 文献[5] 算法 | 10 | 0.161 | 0.140 | 0.140 | 0.144 | 0.169 | 0.188 | 0.192 | 0.165 | 0.189 | 0.129 |
| 50 | 0.256 | 0.567 | 0.154 | 0.143 | 0.129 | 0.188 | 0.55 | 0.124 | 0.135 | 0.534 | |
| 100 | 0.541 | 0.34 | 0.143 | 0.116 | 0.86 | 0.56 | 0.142 | 0.143 | 0.35 | 0.451 | |
| 注:文献[5]算法时间效率在其调节因子α=0.26的基础上测得。 | |||||||||||
本文算法利用点云数目上限在相应坐标轴方向对点云空间自适应分块,尽量避免子空间内存在较多的采样点。用待搜索点到子空间6个面(非整个点云空间边界)的最小距离生成自身小立方体,当其内k邻域候选点数目不满足要求时,根据循环次数和边长增量调节因子动态改变小立方体大小,直至其内点云数目满足要求,尽量降低浮点运算的计算量。当子空间内存在搜索不成功的点时,对子空间6个面有选择地扩展,并对扩展步长自适应计算。实验结果表明,本文算法不仅对子空间点云数目上限、采样密度、控制阈值的左右调节因子、模型拓扑结构都具有较强的稳定性,而且和已有算法相比在搜索速度上有明显的优势,有很高的理论参考价值和实用性。此外,算法中子空间边长增量调节因子b的分布具有很高的规律性。但本文算法也存在一定的不足,如设定的阈值虽然能适应大多数模型,但是这些值的设定并不连续,可能并未使算法效率达到最佳,如何在有限的条件下自适应地确定阈值将是未来进一步分析和解决的主要问题。
| [1] | Zhou Rurong, Zhang Liyan, Su Xu, et al. Algorithmic Research on Surface Reconstruction from Dense Scattered Points[J]. Journal of Software, 2001, 12(2):249-255(周儒荣, 张丽艳, 苏旭, 等. 海量散乱点的曲面重建算法研究[J]. 软件学报, 2001, 12(2):249-255) |
| [2] | Cheng Xiaojun, He Guizhen. The Method and Application of Hole Boundary Extraction for Multi-valued Surface Repair[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6):831-837(程效军, 何桂珍. 适用于多值曲面修复的空洞边界提取方法及应用[J]. 测绘学报, 2012, 41(6):831-837) |
| [3] | Xiong Bangshu, He Mingyi, Yu Huajing. Algorithm for Finding k-nearest Neighbors of Scattered Points in Three Dimensions[J]. Journal of Computer-Aided Design and Computer Graphics, 2004, 16(7):909-912(熊邦书, 何明一, 余华璟. 三维散乱数据的k个最近邻域快速搜索算法[J]. 计算机辅助设计与图形图像学报, 2004, 16(7):909-912) |
| [4] | Piegl L A, Tiller W. Algorithm for Finding All k Nearest Neighbors[J]. Computer-Aided Design, 2002, 34(2):167-172 |
| [5] | Zhao Jianhui, Long Chengjiang, Ding Yihua, et al. A New k-nearest Neighbors Search Algorithm Based on 3D Cell Grids[J]. Geomatics and Information Science of Wuhan University, 2009, 34(5):615-618(赵俭辉, 龙成江, 丁乙华, 等. 一种基于立方体小栅格的k邻域快速搜索算法[J]. 武汉大学学报·信息科学版, 2009, 34(5):615-618) |
| [6] | Ma Juan, Fang Yuanming, Zhao Wenliang, et al. Algorithm for Finding k-nearest Neighbors Based on Spatial Sub-cubes and Dynamic Sphere[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3):358-362(马娟, 方源敏, 赵文亮, 等. 利用空间微分块与动态球策略的k邻域搜索算法研究[J]. 武汉大学学报·信息科学版, 2011, 36(3):358-362) |
| [7] | Liu Yuehua, Liao Wenhe, Liu Hao. Research of k-nearest Neighbors Search Algorithm in Reverse Engineering[J]. Machinery Design and Manufacture, 2012, 1(3):256-258(刘越华, 廖文和, 刘浩. 逆向工程中散乱点云的k邻域搜索算法研究[J]. 机械设计与制造, 2012, 1(3):256-258) |
| [8] | Sarkar M, Leong T Y. Application of k-nearest Neighbors Algorithm on Breast Cancer Diagnosis Problem[C]. The 2000 AMIA Annual Symposium, Los Angeles, CA, 2000 |
| [9] | Connor M, Kumar P. Fast Construction of k-nearest Neighbor Graphs for Point Clouds[J]. IEEE Transactions on Visualization & Computer Graphics, 2010, 16(4):599-608 |
| [10] | Sankaranarayanan J, Samet H, Varshney A. A Fast All Nearest Neighbor Algorithm for Applications Involving Large Point-Clouds[J]. Computers & Graph, 2007, 31(2):157-174 |
| [11] | Procpiuc O, Agarwal P K, Arge L, et al. Bkd-tree:A Dynamic Scalable Kd-tree[C]. International Symposium on Spatial and Temporal Databases, Berlin, Germany, 2003 |
| [12] | Xiao Hui, Yang Bisheng. An Improved KNN Search Algorithm Based on Road Network Distance[J]. Geomatics and Information Science of Wuhan University, 2008, 33(4):437-439(肖晖, 杨必胜. 一种改进的基于道路网络距离的K近邻查询算法[J]. 武汉大学学报\5信息科学版, 2008, 33(4):437-439) |
| [13] | Dickerson M T, Drysdale R, Sack J R. Simple Algorithms for Enumerating Interpoint Distance and Finding k Nearest Neighbors[J]. International Journal of Computational Geometry and Applications, 1992, 2(3):221-239 |
| [14] | Goodsell G. On Finding p-th Nearest Neighbors of Scattered Points in Two Dimensions for Small p[J]. Computer Aided Geometric Design, 2000, 17(4):387-392 |
| [15] | Ma Liming, Xu Yi, Li Zexiang. Fast k-nearest Neighbors Searching Algorithm for Scattered Points Based on Dynamic Grid Decomposition[J]. Computer Engineering, 2008, 34(8):10-11(马骊溟, 徐毅, 李泽湘. 基于动态网格划分的散乱点k邻域快速搜索算法[J]. 计算机工程, 2008, 34(8):10-11) |
| [16] | Yang Jun, Lin Yanlong, Wang Yangping, et al. Fast Algorithm for Finding The k-nearest Neighbors of A Large-Scale Scattered Point Cloud[J]. Journal of Image and Graphics, 2013, 18(4):399-406(杨军, 林岩龙, 王阳萍, 等. 大规模散乱点的k邻域快速搜索算法[J]. 中国图象图形学报, 2013, 18(4):399-406) |
 2016, Vol. 41
2016, Vol. 41


