文章信息
- 张晗, 倪维平, 严卫东, 边辉, 吴俊政, 李莎, 金骁
- ZHANG Han, NI Weiping, YAN Weidong, BIAN Hui, WU Junzheng, LI Sha, JIN Xiao
- 利用分形和多尺度分析的中低分辨率SAR图像变化检测
- Mid and Low Resolution SAR Image Change Detection Based on Fractal and Multi-scale Analysis
- 武汉大学学报·信息科学版, 2016, 41(5): 642-648
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 642-648
- http://dx.doi.org/10.13203/j.whugis20140375
-
文章历史
- 收稿日期: 2014-09-15

2. 西安电子科技大学电子工程学院, 陕西 西安, 710071;
3. 沈阳炮兵学院, 辽宁 沈阳, 110161
2. School of Electronic Engineering, Xidian University, Xi'an 710071, China;
3. Shenyang Artillery Academy, Shenyang 110161, China
合成孔径雷达(synthetic aperture radar,SAR)系统具有全天时、全天候、覆盖范围大的工作特性,因而在变化检测等地物动态分析方面的应用越来越广泛。一般而言,SAR图像变化检测技术可分为像素级和对象级两种类型[1]。前者先构造差异图,然后,将差异图分割成变化和未变化区域;后者先对二时相图像分别分割,通过比较对应分割块间的差异实现变化检测。
像素级变化检测主要包括差异图构造和差异图分割两步[2]。常见的差异图构造方法包括差值、比值、相关系数、图像熵等[1, 2, 3]。不同于光学图像,SAR图像固有的乘性相干噪声严重影响了图像解译,因此,克服斑点噪声干扰是SAR图像变化检测需要解决的关键问题。均值对数比(log ratio,LR)差异图通过将乘性噪声转换为加性噪声,结合取平均的方法,一定程度上克服了斑点噪声的影响[2]。文献[3]利用SAR图像的局部统计特性,定义聚合交叉熵(Kullback-Leibler divergence,KLD)为变化检测差异图,也取得了较好的效果。但LR差异图上的噪声强度仍是不可忽视的,而对于城区SAR图像而言,KLD计算出的局部统计特性差异难以反映变化对象的结构信息。SAR图像中每个像素的灰度值都是相应分辨单元内所有回波信号相干叠加后的结果,其特性可用空间混沌模型中的分形维数描述[4, 5]。研究发现,不同类型自然地物SAR图像的分形值相差较小,而具有结构性和强散射性的人造目标分形值与自然目标分形值差异较大,因此分形图能够将人造目标从复杂自然背景中区分出来。借助主成分分析(principal component analysis,PCA)方法将分形维数引入到差异图的构造过程中,本文定义了分形-对数比(fractal dimension-log ratio,FD-LR)融合差异图。
相比对差异图构造方法的研究,对差异图分割算法的探索更为广泛,主要有阈值分割和聚类两种类型[6, 7, 8, 9],本文采用前一种方法。模型选择及参数估计是阈值分割的关键,鉴于同类地物目标的分形值具有高斯分布的特点[5],本文采用混合高斯模型(mixed Gaussian model,MGM)对FD-LR进行统计建模,借助期望最大化(expectation maximization,EM)算法估计模型参数,进而利用贝叶斯最大后验概率准则(maximum a posteriori,MAP)确定分割阈值。为兼顾SAR图像的多尺度特性,降低斑噪干扰,本文结合多尺度分析和决策级融合的方法得到最终的变化检测结果。算法主要流程为:首先分别计算二时相图像数据的对数比差异图LR和分形差异图FD,然后计算向量[LR FD]的第一主成分分量,得到分形-对数比融合差异图FD-LR,最后结合多尺度分割和决策级融合的方法得到变化检测结果。
1 方法描述 1.1 差异图构造 1.1.1 SAR图像的分形维数作为一种主动式成像的遥感系统,SAR图像像素值是地面上每个分辨单元内成千上万个回波相干叠加的结果:
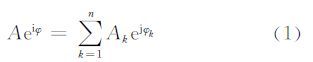
叠加过程类似于复平面上的随机行走过程,其中Ak、φk分别是第k步随机行走的长度和方向。研究表明,随机行走过程可以用Hurst指数为0.5的Brownian运动来描述,从而可以将SAR图像看做一个混沌模型,并且用分形维数来描述[4, 5]。
设A是Rn的一个子集,A的整体包含很多自相似的球,包括A的所有值。令Nr为尺度为r的球的个数,则分形维数F定义为:
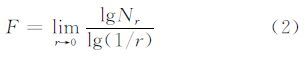
图像分形维数的计算主要有盒维法、方差法和频谱法三类,其中差分盒维法(differential boxing counting,DBC)因物理含义明确且计算简单而得到广泛应用[10, 11]。将大小为M×M的图像看成一个由(x,y,z)表示的三维模型,其中(x,y)是像素位置构成的二维平面,(z)是由起伏的图像灰度曲面构成的第三维。将(x,y)平面分成不重叠的s×s大小的图像块,图像块的尺度r=s,且1<s<M/2,计算式(2)中Nr的步骤为:将每个图像块上的第三维(z)依灰度值分割成高度为s′的小段,构成了ceil(G/s′)个s×s×s′大小的盒子,其中G是图像块中的最大灰度值。假设第(i,j)图像块中最小和最大灰度值分别落在第k个和第l个盒子中,则覆盖这个图像块的盒子个数为:
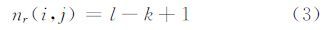
计算不同尺度r下的Nr,利用最小二次线性拟合的方法,求得lgNr和lg(1/r)之比,即得到分形维数F。
分形散射的研究表明,散射表面的分维特性将携带到散射信号中去,因此地物散射信号的分形维数能够反映地物的分维结构[5, 12]。在分形理论应用中,自然背景由极不规则的复杂环境构成,其相干叠加过程较复杂,分形维数较高;而人造目标一般表现为相对规则的几何单元,只包含少数次散射叠加过程,其分形维数较低。SAR图像上人造地物和自然地物的分形维数具有明显的可分性。利用DBC计算图 1(a)所示SAR图像的分形维数,结果见图 1(b)。可以看到自然地物的分形值差异较小,而建筑的分形值与周围环境形成明显差别,且轮廓特征清晰。SAR图像的分形图能够用于从复杂环境中提取建筑目标。

|
| 图 1 SAR图像及其分形图像 Fig. 1 SAR Image and the Corresponding Fractal Image |
分形图能够区分建筑目标和自然地物,但对不同类型自然地物的区分度较差,而对数比差异图在该方面则具有优势。因此,本文定义了分形-对数比融合差异图,以期同时获得对自然地物和人造目标的有效区分。
设I1、I2是同一地区、同一传感器下的二时相SAR图像,其对数比差异图定义为:
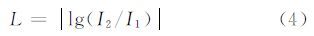
利用DBC算法分别计算两幅图像的分形图F1、F2,定义分形差异图为:
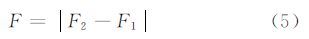
分别对L和F进行均值归一化处理后,在每个像素位置处,[L(i,j)F(i,j)]构成一个二维特征向量。为得到唯一确定的差异图像,需要将二维特征向量融合成起来。本文定义融合差异图FD-LR为二维特征向量[L(i,j) F(i,j)]PCA变换后的第一主成分分量P1。
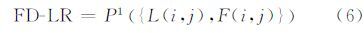
第一主成分分量FD-LR将对数比差异图和分形差异图中的变化信息线性地融合起来,使其更趋稳定、能量更趋集中,涵盖了不同地物类型的变化,从而适用于复杂地物SAR图像的变化检测。此外,PCA变换还起到了降噪的作用。
1.2 差异图分割 1.2.1 分割规则文献[5]提出,同一组数据不同数据段的分形维数服从高斯分布,因此分形差异图上的变化和非变化类分别服从高斯分布。为简化模型,本文进一步假设,FD与LR线性组合得到的第一主成分分量FD-LR中变化wc和非变化类wu都为高斯分布,从而FD-LR(i,j)服从混合高斯分布,下面用D(i,j)表示FD-LR(i,j),相应的概率密度函数为:
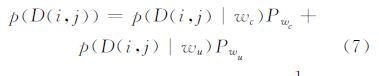
式中,p(D(i,j)|w)=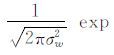
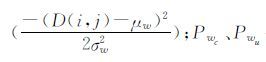 分别表示变化类和非变化类像素的概率;μwc、σwc为变化类的均值和标准差;μwu、σwu为非变化类的均值和标准差。
分别表示变化类和非变化类像素的概率;μwc、σwc为变化类的均值和标准差;μwu、σwu为非变化类的均值和标准差。
用EM算法估计上述6个参数,依据贝叶斯最大后验概率准则 (MAP),得到分割结果图C(i,j):
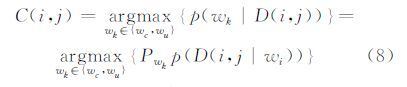
多尺度分析是图像解译的重要工具。文献[6]利用对偶树小波变换提取对数比差异图的低通和高通信号,分别进行阈值分割后,求并集得到最终的变化检测结果。但实验证明,FD-LR差异图中的高通信号包含的变化信息较少,考虑到算法效率可以忽略不计。本文通过构建多尺度空间,利用FD-LR在不同尺度下的低通信息,结合决策级融合的方法得到变化检测结果,在降低分割算法时间复杂度的同时,保证了较好的检测性能。
对差异图像D(i,j),利用尺度空间核G(i,j,s)进行卷积运算,得到尺度s下的图像信号Ds(i,j):
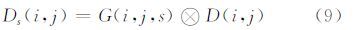
尺度空间核要求对于所有输入信号D,与卷积核G(s)卷积后的输出信号Ds的极值数不超过原信号的极值数。文献[13]利用扩散方程描述尺度空间滤波过程,由此证明了高斯卷积核是实现尺度变换的唯一变换核,尺度参数s由高斯核的标准差决定。高斯卷积核表示为:
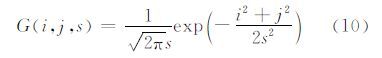
对于N个不同尺度sk下的差异图{Ds1,Ds2,…,DsN},分别用MAP算法估计阈值,得到分割结果为{Ms1,Ms2,…,MsN}。多尺度融合结果定义为:
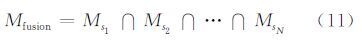
随着尺度的增大,图像上的噪声不断减少,同时目标也越来越模糊,MAP分割出的目标区域比实际的目标区域大。在尺度参数选择适当的前提下,求交集运算能够保留精细尺度下的目标结构特征,同时除去噪声产生的误检。尺度空间参数S={s1,s2,…,sN}的选取是本文算法中唯一可调参数,并且直接影响检测精度。
2 实验结果与分析为检验算法性能,本文比较了LR、KLD、FD-LR三种差异图对不同类型变化的检测效果,利用受试者工作特征(ROC)曲线客观评估了三种差异图的变化检测能力,并通过实验分析的方法选择高斯多尺度参数。将本文提出的FD-LR多尺度阈值分割算法的变化检测结果,与文献[6]的对偶树小波变换多尺度变化检测方法(DT-CWT),以及文献[2]基于修正MRF能量函数的模糊聚类(MRF- FCM)方法进行比较。
2.1 差异图生成实验本文从两对SAR影像中截取变化区域,如图 2~3所示。其中,图 2(a)、2(b)分别是1999年5月和6月ERS-2获取的Bern地区水灾前后的SAR图像对截图,图像分辨率为12.5 m,图像大小为301×301像素;图 3(a)、3(b)分别是2008年3月3日和6月16日ESA/ASAR获取的5·12汶川地震前后的SAR影像对截图(表示为WC),图像分辨率为10 m,大小为256×256像素,图中的变化为震后新增建筑。用手动阈值和人工去噪的方法[6]得到变化参考图如图 2(c)、3(c)所示。
|
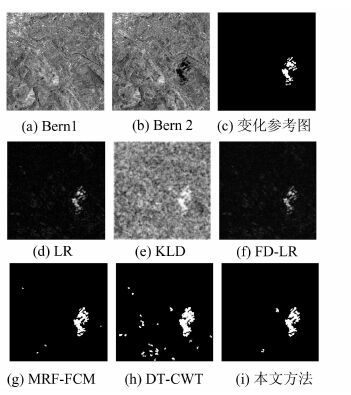
| 图 2 Bern图像差异图及变化检测结果 Fig. 2 Difference Image and Change Detection Results on Bern SAR Images |
|
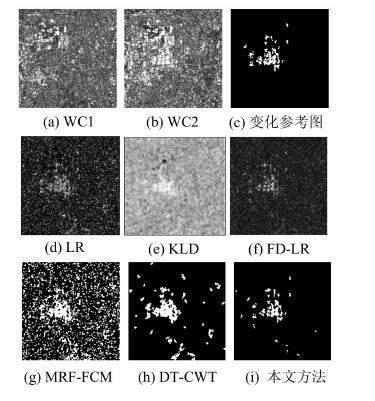
| 图 3 WC图像差异图及变化检测结果 Fig. 3 Difference Image and Change Detection Results on Wenchuan SAR Images |
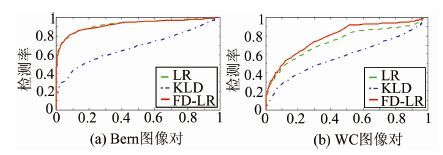
构造上述两组SAR图像的差异图,如图 2(d)~2(f)、3(d)~3(f)所示。其中,LR用3×3像素大小的平滑窗[2],KLD用7×7像素大小的统计窗[3]。可以看出,对于图 2(a)、图 2(b)中的水体变化,3种差异图的检测效果相当;而对于图 3(a)、3(b)中的建筑变化,LR差异图的斑噪水平较强;KLD差异图虽然较为平滑,但不能保持变化目标的轮廓特征;而FD-LR具有明显的建筑区斑噪抑制效果,不仅可以有效提取出不同地物类型的变化,并且提取的建筑目标变化具有清晰的轮廓结构,这正是受益于分形差异图对具有规则形状和强散射特性的人造目标的识别能力。绘制两组图像对应的受试者工作特性(ROC)曲线(见图 4),可以看出,相比其他两种差异图,KLD的检测能力较差。对于包含水域变化的自然地物,LR和FD-LR的检测能力不相上下,而对于包含建筑变化的人造地物,FD-LR的检测能力要高于LR,从而量化地证明了FD-LR相对于其他两种差异图具有更好的适用性。
|
| 图 4 ROC曲线 Fig. 4 ROC Curves |
在SAR图像变化检测应用中,多尺度分析的目的是降低相干斑的影响,提高变化检测精度。而实际上不同分辨率、不同波段SAR图像的噪声强度不同,理论上应根据噪声强度选择尺度参数。但实验结果表明,适当的尺度组合能够保证对不同斑噪水平SAR图像变化检测性能的鲁棒性。同文献[6, 8]中小波多尺度分析过程相似,本文同样用实验的方法确定高斯多尺度参数。SAR图像的噪声强度通常用等效视数(ENL)表示,ENL越小,表明斑噪越强。计算得到Bern图像的ENL为12.5,WC图像为7.3,即Bern图像的噪声较弱,而WC图像的噪声相对较强。
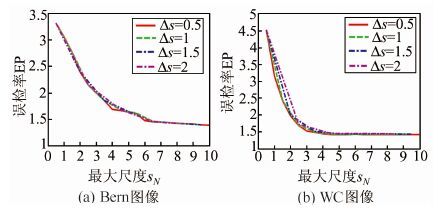
尺度空间构建的过程实际上就是确定高斯卷积核的标准差序列S={s1,s2,…,sN}的过程,其中si<si+1。尺度层数N越大,尺度层间差异Δs=si+1-si越小,则尺度空间对图像的描述也越准确,但同时会降低算法运行效率。借鉴文献[6]的方法,本文绘制了上述两组图像对的误检率EP与最大尺度sN及尺度层差Δs之间的关系,如图 5所示。其中,误检率EP定义为漏警和虚警像素占全部图像像素的百分比。曲线上的每一个点表示在尺度空间S={s1,s1+Δs,s1+2·Δs,…,sN}上,利用§1.1.2所述的多尺度分割和决策级融合方法进行变化检测的误检率。为了得到算法精度和运算效率的平衡,本文取N=3,即构建3层尺度空间。为降低尺度为0的原始图像噪声干扰,取s1=0.5作为第一层尺度。可以看出,随着sN的增大,两组图像的误检率都逐渐降低,并最终达到平稳状态。Δs取最小值0.5时,误检率最低,此后随Δs的增大EP逐渐变高。对于Bern图像组,EP的变化较为平缓,在sN∈[0.5,10]的区间内,EP值的变化幅度小于2%,且Bern图像组的EP受Δs影响较小。这正是因为Bern图像组的ENL较大,斑噪强度低,因而对尺度的敏感性不强。WC图像组的EP值对sN更敏感,特别是当sN<2时,EP随sN的增大急剧降低,这源于多尺度分析的降斑作用。观察发现,图 5中两组EP曲线都在sN=2处出现拐点,此后EP的变化速度变缓,这一现象说明尺度空间S={0.5,0.5+Δs,0.5+2·Δs,…,2}能够反应图像的主要变化特征。鉴于此,本文取s2=2。sN≥6时,两组EP曲线都达到了平稳状态,适当放宽之后取s3=sN=7。至此,本文确定了三层空间的尺度参数S={0.5,2,7}。虽然参与尺度分析的实验数据有限,但后续实验结果证明了其有效性。
|
| 图 5 误检率与尺度参数关系曲线 Fig. 5 EP-S Curves |
用MRF-FCM方法、DT-CWT方法,以及本文的高斯多尺度分析方法对上述两组数据进行变化检测,结果如图 2(g)~2(i)、图 3(g)~图 3(i)所示,算法在Intel (R) Core (TM) i7-2600 @ 3.4 GHz处理器上的运行时间如表 1所示。其中,前两种方法均是用对数比图作差异图,本文方法用FD-LR作差异图。为客观评估算法有效性,将上述3种方法分别用于LR差异图和FD-LR差异图的分割,计算6种检测结果的误检率如表 1的后两列所示。
| 图像对 | 方法 | 运算时间/s | 误检率/% | ||
| LR | FD-LR | ||||
| Bern | MRF-FCM | 21.2 | 0.68 | 8.27 | |
| DT-CWT | 9.2 | 2.13 | 1.73 | ||
| 本文方法 | 9.8 | 2.00 | 1.45 | ||
| WC | MRF-FCM | 90.1 | 21.03 | 14.61 | |
| DT-CWT | 7.1 | 4.31 | 2.68 | ||
| 本文方法 | 7.4 | 3.20 | 1.49 | ||
可以看出,3种方法中,MRF-FCM对包含水域变化的Bern图像的变化检测效果较好,而对包含建筑变化的WC图像检测结果不理想,虚警率很高,这是因为水域变化差异图上的变化像素与未变化像素间具有较大的对比度;而建筑变化的对数比值较小,使得对数比差异图上的变化像素与受斑点噪声干扰的其他未变化像素的对比度不够高,导致迭代运算陷入了局部最优。DT-CWT对两组图像的检测效果都较好,说明DT-CWT算法对不同地物类型的变化有更好的鲁棒性,这得益于DT-CWT算法的小波多尺度分析过程,而本文提出的基于FD-LR差异图的高斯多尺度分析方法在两组实验图像上都具有最好的检测效果。这首先源于FD-LR差异图具有比LR差异图更好的检测性能,其次得益于有效的高斯多尺度分析和决策级融合方法。从表 1所示的运算时间上看,MRF-FCM方法因为涉及到迭代运算,运算效率最低。本文算法的运算时间比DT-CWT方法稍长。实际上,由于DT-CWT算法需要同时对低通和高通波段进行变化检测,其分割运算时间是本文算法的2倍。而本文方法的差异图构造过程需要计算图像的分形维数,占据了主要的运算时间。
比较不同检测方法的误检率可以看到,MRF-FCM方法用于Bern图像水体变化的误检率较低,用于建筑变化图像的误检率很高,DT-CWT方法对两种类型变化的检测有更好的鲁棒性,而本文方法的误检率比其他两种方法都要低。此外,无论是DT-CWT分割还是本文的高斯多尺度分割,其在FD-LR上的误检率都要低于在LR上的误检率,说明了FD-LR的优越性。而无论用FD-LR还是LR作差异图,高斯多尺度分割的误检率都低于DT-CWT的分割误检率,从而证明了高斯多尺度分割方法的优势。在3层尺度空间S={0.5,2,7}下,两组图像的误检率都基本达到了图 5所示误检率曲线的最小值,从而表明了本文的尺度参数选择是有效的。
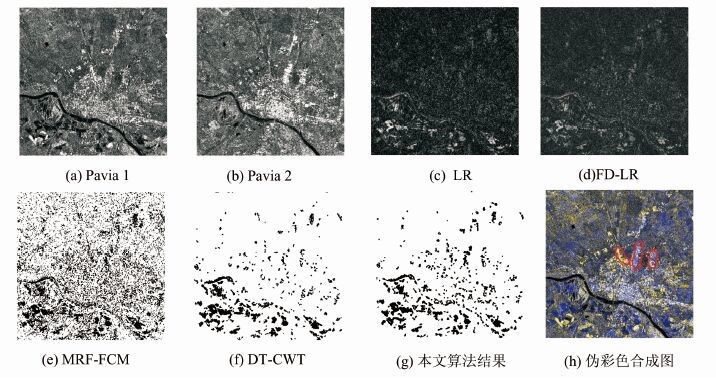
为进一步检验本文算法用于复杂场景变化检测的性能,本文还选取了一组地形复杂的城区SAR图像对,如图 6所示。图 6(a)、6(b)分别为Radarsat-1和ERS-2获取的意大利Pavia城区水灾及洪水退去后的SAR图像,图像大小为730×730像素。图像对应的LR和FD-LR差异图分别如图 6(c)、6(d)所示,其中主要包括了水体变化及部分建筑遭到水淹的变化。由于变化情况较为复杂,难以绘制参考图像,本文利用伪彩色的方法得到图 6(h)所示的合成图,其中R和G通道为第1时相数据,B通道为第2时相数据,因而合成图像上黑色、灰色和白色区域均为未变化区,蓝色为灰度值增大的变化区,黄色为灰度值降低的变化区。受斑噪影响,图像上的未变化区域存在黄色或蓝色噪声,而有效变化区则是蓝色和黄色较集中的位置。利用上述3种算法进行变化检测,结果如图 6(e)、6(f)、6(g)所示。
可以看出,3种方法中,MRF-FCM的检测结果中有大量噪声产生的虚警,DT-CWT方法的检测结果与本文方法在图像左下角的水域变化部分效果相当,而基于LR差异图的DT-CWT方法在图 6(h)上红色标注位置处的建筑变化位置存在漏警。这是因为在8 bits图像上,水体变化(0~40)在对数比差异图上的值显然远高于建筑变化(40~255)。当复杂地物图像上同时存在水体和建筑的变化时,水体的变化往往会“掩盖”建筑的变化,这一点也可以从图 6(c)、6(d)的比较中看出。由此证明本文提出的FD-LR差异图比LR差异图更适合复杂场景SAR图像变化检测,同时本文提出的高斯多尺度分析和决策级融合分割方法具有不逊于小波多尺度分析的分割效果。
|
| 图 6 复杂城区地形变化检测结果 Fig. 6 Change Detection Results on Complex City Area |
上述实验证明了本文算法用于SAR图像变化检测的有效性,其优势主要体现在两个方面:(1) 通过将分形差值引入到差异图的构建过程,有效地将人造目标的变化从复杂的自然地物变化中凸显出来。同时,结合对数比差异图在自然地物变化检测方面的优势,本文算法能够适用于复杂场景的变化检测。(2) 得益于SAR图像上同类地物的分形值服从高斯分布的特点,本文验证了用混合高斯模型对FD-LR差异图建模的有效性,借助高斯多尺度分割和决策级融合的方法,在不降低运算效率的前提下(同DT-CWT小波多尺度分析方法相比)提高了变化检测精度。实际上,本文所用实验图像的分辨率都在10 m左右,属于中低分辨率SAR影像,没有验证算法是否适合高分辨率SAR图像的变化检测,这将是下一步的工作方向。
3 结 语本文将分形维数差值图与对数比图相融合,定义了一种新的变化检测差异图FD-LR。FD-LR对自然地物和建筑物等人造目标的变化都有较好的检测效果,特别适用于中低分辨率复杂场景SAR图像的变化检测。此外,高斯多尺度分析和决策级融合的方法进一步降低了噪声的干扰。对比实验证明本文算法对不同地物类型的变化都具有较好的适用性。下一步将继续研究本文算法在高分辨率SAR影像变化检测方面的有效性,以及其他与分形相关的差异图融合方法。
| [1] | Li Deren. Change Detection from Remote Sensing Images[J]. Geomatics and Information Science of Wuhan University, 2008, 28(s1):7-12(李德仁. 利用遥感影像进行变化检测[J]. 武汉大学学报·信息科学版, 2003, 28(s1):7-12) |
| [2] | Gong M G, Su L Z, Jia M,et al. Fuzzy Clustering with Modified MRF Energy Function for Change Detection in Synthetic Aperture Radar Images[J]. IEEE Transactions on Fuzzy Systems,2013, 99:1-12 |
| [3] | Inglada J, Mercier G. A New Statistical Similarity Measure for Change Detection in Multitemporal SAR Images and Its Extension to Multiscale Change Analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(5):1432-1445 |
| [4] | Huang S Q, Cai X H, Chen S X,et al. Change Detection Method Based on Fractal Model and Wavelet Transform for Multi Temporal SAR Images[J]. International Journal of Applied Earth Observation and Geoinformation, 2011, 13(1):863-872 |
| [5] | Salmasi M, Hashemi M M. Design and Analysis of Fractal Detector for High Resolution Radars[J]. Chaos, Solitons, and Fractals, 2009, 40(1):2133-2145 |
| [6] | Celik T. A Bayesian Approach to Unsupervised Multiscale Change Detection in Synthetic Aperture Radar Images[J]. Signal Processing, 2010, 90:1471-1485 |
| [7] | Xin F F, Jiao L C, Wang G T. SAR Image Change Detection Based on Memetic Algorithm[J]. J Infrared Millim Waves,2012,31(1):67-72(辛芳芳, 焦李成, 王桂婷. 基于Memetic算法的SAR图像变化检测[J]. 红外与毫米波学报, 2012, 31(1):67-72) |
| [8] | Bovolo F, Bruzzone L. A Detail-Preserving Scale-Driven Approach to Change Detection in Multitemporal SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(12):2963-2972 |
| [9] | Gong Maoguo, Zhou Zhiqiang, Ma Jingjing. Change Detection in Synthetic Aperture Radar Images Based on Image Fusion and Fuzzy Clustering[J]. IEEE Transactions on Image Processing, 2012, 21(4):2141-2151 |
| [10] | Chaudhuri B, Sarkar N. TextureSegmentation Using Fractal Dimension[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence Geoscience and Remote Sensing, 1995, 17(1):72-77 |
| [11] | Ivanovici M, Richard N. Fractal Dimension of Color Fractal Images[J]. IEEE Transactions on Image Processing, 2011, 20(1):227-235 |
| [12] | Pentland A P. Fractal-Based Description of Natural Scenes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence Geoscience and Remote Sensing, 1984, 6(6):661-674 |
| [13] | Koenderink J J. The Structure of Images[J]. Biological Cybernetics, 1984, 50:363-370 |
 2016, Vol. 41
2016, Vol. 41


