文章信息
- 何立新, 孔斌, 杨静
- HE Lixin, KONG Bin, YANG Jing
- 单目图像内静态物体深度的自动测量方法
- An Automatic Method of the Depth Measurement of Static Objects in a Monocular Image
- 武汉大学学报·信息科学版, 2016, 41(5): 635-641
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 635-641
- http://dx.doi.org/10.13203/j.whugis20140656
-
文章历史
- 收稿日期: 2015-05-06

2. 中国科学院合肥智能机械研究所, 安徽 合肥, 230031;
3. 合肥学院网络与智能信息处理重点实验室, 安徽 合肥, 230601
2. Hefei Institute of Intelligent Machines, Chinese Academy of Sciences, Hefei 230031, China;
3. The Key Lab of Network and Intelligent Information Processing, Hefei University, Hefei 230601, China
从二维平面图像中提取深度信息是立体视觉的重要研究内容,有时需要提取二维图像中的每个像素点的深度信息,而更多时候则只要获取其中的感兴趣物体的深度信息即可,例如在机器人行进中的障碍物距离、红绿灯距离无人车的距离等。
提取深度时可以利用双目视差信息、线条透视信息、散焦信息和图像的纹理信息等[1, 2, 3]。文献[4]在透镜系统中增加一个半镀银反射镜获取同一场景的光圈大小不同的两幅图像,其中一幅是针孔成像,然后利用散焦信息提取了物体的边缘深度,该方法对成像要求较高,需要对相机进行改装。文献[5]从一幅图像中用散焦信息提取图像的密集深度图,但所获取的深度信息有不少地方不精确,甚至差距很大。文献[6]提出了采用单目相机获取图像中的物体深度,该方法需要在旋转相机前后各获取一幅图像,再计算图像的匹配点,从而获得深度信息。而使用双目视差信息获取物体深度需要使用两个相机,且需要知道它们的精确位置,在两幅图像中查找特征点并进行匹配,然后用几何关系求出深度信息。该方法计算量大,且当在图像中的某个物体上找不到可以匹配的特征点时则无法求出该物体的深度信息,现有的立体视觉产品Bumblebee就是利用双目视差信息,其价格昂贵。
为了避免双目深度中的大运算量的角点匹配和散焦深度信息中的多处不精确等问题,本文提出了采用单目相机自动测量图像内静止物体的深度信息的方法:首先,使用一个普通相机,在拍摄第一幅图像后保持相机的所有参数不变,并使相机沿光轴方向移动一段距离d后拍摄第二幅图像;其次,利用水平集方法将图像中的物体分割出来,并将物体像的熵和Hu氏不变矩结合起来实现物体的自动匹配;最后,根据本文推导的公式求出物体深度。
1 图像中静态物体深度测量的基本原理与流程相机成像的基本原理为:

其中,f为焦距;u为物距;v为像距。
假设第一次成像时的物距为u,物体成像的高度为h像1,第二次成像时的物距为u+d,物体成像的高度为h像2,如图 1所示,相机在两次成像时所有参数保持不变,则两次成像的像高存在如下关系:

|
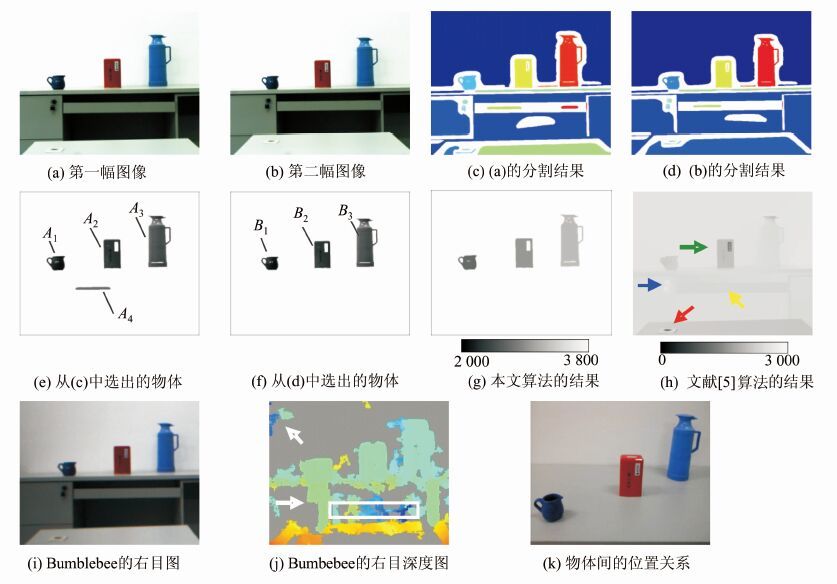
| 图 1 物体深度测量的各阶段结果图及算法结果的对比 Fig. 1 Steps Results of Measurement of Objects Depth and Comparison of Our Method with the Others’ |
其中,k>0且k∈R,R为实数集。
由相机成像的基本原理和三角几何知识可知:

由于相机的薄凸透镜是关于透镜中心对称的,所以物体上的各点经过相机成像时的缩放率是相同的,并假定物体所成的像完全在图像内部(即没有像素在图像的4个边界上),因此,由微积分知识可以证明下式成立(在极坐标下证明更简洁):

其中,S像1和S像2为图中某个物体分别在第一、二次成像时的面积。
由式(3)、(4)可知:

由式(2)、(5)可知:

本文所提出的测量物体深度方法,主要包括7步。
1) 保持相机参数不变的条件下,在物距为u和u+d时分别获取一幅图像;
2) 对这两幅图像进行图像分割,分别在每幅图像中得到若干个物体的像(即分割区域);
3) 判断每个物体的像是否完全在图像的内部,为否则删除该物体,是则保留;
4) 计算每个物体的像面积S;
5) 设St为面积阈值(本文实验中St=图像的总面积/400),逐一判断S>St是否成立,为否则删除该物体,是则保留。因为拍照时都会聚焦于要测量的物体,所以该物体的像的面积不会太小,且若物体像的面积过小,则对噪声敏感,导致深度测量精度不足;
6) 将物体像的熵和加权Hu氏不变矩结合起来用于匹配同一物体在两幅图像中的像;
7) 用式(6)求解出各个物体深度。
2 基于LBF模型的图像分割目前图像分割的方法很多,本文采用局部二值拟合能量(local binary fitting energy,LBF)模型[7, 8]分割方法,因为该方法利用了图像的局部灰度信息,对灰度不均匀的图像分割效果较好。LBF模型中建立了以高斯函数为核函数的局部双重拟合能量泛函,对于图像内任意一个像素点x,LBF模型的能量泛函为:

其中,C为闭合曲线;in(C)和out(C)分别为闭合曲线内部区域和外部区域;f1(x)和f2(x)为像素点 x 在闭合曲线内部区域和外部区域的灰度拟合值;像素点y的取值范围为x-y≤3σ;K为核函数,采用以σ为标准差的高斯函数:

通过能量函数ExLBF(C,f1(x),f2(x))的极小值来求f1(x)和f2(x)的值,从而实现图像分割。
3 物体图像的匹配分割图像后,接下来就要在两幅不同的图像中查找出同一物体所成的像,即进行物体图像的匹配(或分类),该类问题的研究成果较多[9, 10],如利用最小噪声分离[11]、流形学习[12]和基于判别局部增强配准技术[13]等方法实现待处理数据的降维,从而快速有效地进行图像的匹配(或分类)。本文根据所解决问题的需要出发提出将物体像的熵的相对变化率和加权Hu氏不变矩结合起来进行物体的识别和匹配。
3.1 物体像的熵由于这两幅图像仅仅是在两次采集时相机沿着光轴方向移动了一段距离d,其他参数不变,间隔时间也很短,因此同一物体两次成像的颜色或灰度分布是高度相似的,而信息论中的熵可以用来度量图像中的颜色或灰度分布情况,对颜色或灰度分布不同的物体有较好的区分能力。熵的定义为[12]:

式中,L为图像的灰度级数目,通常取256;zi为图像的灰度级,i=0,1,2,…,L-1;p(zi)表示图像中灰度级为zi的像素的概率。
本文提出的物体像的熵和通常所说的图像的熵略有不同,图像的熵是指计算包含图像内的物体和背景的整个图像区域的熵值,该区域为矩形;而物体像的熵则是指仅仅计算图像内的物体所成像的区域的熵值,该区域可以为任意形状,具体由物体形状决定。令:

式中,rO表示物体像的熵的相对变化率;rI表示图像熵的相对变化率;e1O和e2O分别表示同一物体在第1、2次成像的物体像的熵;同理,e1I和e2I分别表示同一物体在第1、2次成像的图像的熵。本文共用15组图像进行实验,表 1中是这15组(共含42个物体)场景的每一场景先后2次成像的两种不同的熵的相对变化率的比较数据,在各类数值中rO要远小于rI,可见物体像的熵更稳定,能更精确地反映物体本身的灰度分布,rO比rI更适合用于物体图像的匹配。
| 最大值 | 最小值 | 平均值 | |
| rI | 0.233 980 | 0.054 847 | 0.120 103 |
| rO | 0.028 094 | 0.000 107 | 0.005 819 |
| rI/rO | 8.33 | 512.59 | 20.64 |
由于测量的是静态物体的深度,故物体的形状是不变的。而Hu提出的7个不变矩具有平移、旋转、缩放等不变的性质,可用于物体的识别[14, 15]。
一幅数字图像f(x,y)的二维的p+q阶矩可定义为:

式中,p,q=0,1,2,…。相应的中心矩定义为:

其中,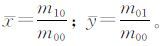
则归一化后的p+q阶矩可定义为:

其中,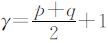 此时,p+q=2,3,…
此时,p+q=2,3,…
由此,Hu等人推导出7个不变矩公式:

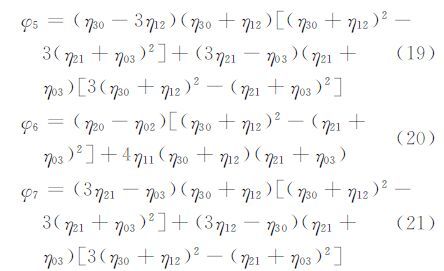
由于高阶矩对图像噪声较为敏感[16],为了减少噪声对不变矩的影响,本文采用加权的不变矩,即:
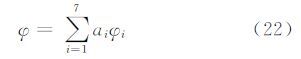
本文实验中取a1=0.4,a2=0.3,a3=0.1,a4=a5=a6=a7=0.05。在匹配时需要用式(23)求物体像的匹配程度,M值越小则匹配程度越高。
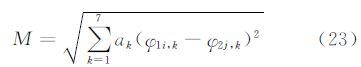
式中,φ1i,k表示第1幅图像中的第i个物体的第k阶不变矩;φ2j,k含义类似。
3.3 匹配判定单独用物体像的熵的相对变化率(方法1)或单独用加权Hu氏不变矩(方法2)进行物体的图像匹配时往往会产生错误匹配,为了获取更高的正确匹配率,本文将这两种方法结合起来使用(方法3),即同时满足式(24)、式(25)的可判定为是同一物体的像。

式中,Tr 和TM分别表示相应的阈值。
表 2中的数据是分别用上述3种方法对15组图像进行物体匹配时产生的错误匹配数的统计与对比,实验时采用了统一的参数Tr=0.03,TM=1.3。
| 组编 号 | 方法 1 | 方法 2 | 方法 3 | 组编 号 | 方法 1 | 方法 2 | 方法 3 |
| G1 | 0 | 2 | 0 | G9 | 4 | 2 | 0 |
| G2 | 4 | 2 | 0 | G10 | 0 | 2 | 0 |
| G3 | 0 | 0 | 0 | G11 | 0 | 6 | 0 |
| G4 | 4 | 0 | 0 | G12 | 2 | 3 | 0 |
| G5 | 0 | 1 | 0 | G13 | 0 | 1 | 0 |
| G6 | 0 | 1 | 0 | G14 | 1 | 2 | 0 |
| G7 | 4 | 2 | 0 | G15 | 1 | 1 | 0 |
| G8 | 4 | 3 | 0 | 合计 | 24 | 28 | 0 |
由表 2可见,方法3的物体匹配效果远好于前面两种方法。这是由于单独使用熵或矩时,仅仅是从物体像的灰度分布或形状数据等单方面进行匹配,此时阈值选取很困难,取值稍大则匹配时易出现一对多的情况,稍小则出现无法找到匹配物体;而综合使用二者时阈值可以选的相对较大,这样不至于漏匹配,如Tr=0.03比表 1中rO均值的5倍还要大,而熵和矩二者的共同作用有效地限制了一对多情况的产生。
以表 2中的G7组为例,图 3(a)是该组图片中的一幅,其中含有4个待测距物体,假设第一、二幅图像中的第i个待测距物体分别记为Ai和Bi,则用上述3种方法的匹配结果如表 3所示,其中*表示得到的错误匹配。由表 3可见,仅用物体像的熵则物体1、2,物体3、4均无法区分,而仅用物体的加权矩则物体1、4无法区分,但是同时用熵和矩就能很好地将这4个物体区分开。
| A1 | A2 | A3 | A4 | |
| 方法1 | B1 B2* | B1* B2 | B3 B4* | B3* B4 |
| 方法2 | B1 B4* | B2 | B3 | B1* B4 |
| 方法3 | B1 | B2 | B3 | B4 |

|
| 图 3 物体深度测量的两组实例图 Fig. 3 Two Group of Example Images of Measurement of Objects Depth |
图 1(a)是用相机拍摄的一幅图像,假定此时物距为u,然后保持相机的各个参数不变沿光轴方向移动d=200 mm的距离,拍摄图像得到图 1(b)。利用LBF模型分别对这两幅图像进行分割,并将分割结果进行彩色标注得到图 1(c)和图 1(d),图 1(c)含有22个物体,图 1(d)含有20个物体,选择其中完全位于图像内部且S>St的物体,得到图 1(e)和图 1(f),分别计算图 1(e)、图 1(f)中的各个物体的7个不变矩、熵值和面积,运用式(24)、(25)可以得到正确的物体匹配,然后用式(6)可求出物体的深度,其具体数据如表 4所示。表 4中的实际距离是通过卷尺测量相机透镜中心到某个物体各个部位的距离,然后计算出的平均距离。深度图如图 1(g)所示,图 1中所有纯白色均表示深度不能确定区域,图 1(g)下面的灰度条表示灰度值与深度值的对应关系。
| 物体编号 | A1 | A2 | A3 | A4 | B1 | B2 | B3 |
| 不变矩φ1 | 5.028 16 | 5.284 08 | 5.605 55 | 4.629 5 | 5.028 41 | 5.285 26 | 5.608 25 |
| 不变矩φ2 | 13.415 1 | 11.942 0 | 11.790 5 | 9.291 7 | 12.897 9 | 11.979 1 | 11.793 7 |
| 不变矩φ3 | 18.882 7 | 20.642 7 | 23.389 4 | 22.697 2 | 19.734 5 | 20.475 5 | 23.545 7 |
| 不变矩φ4 | 19.070 2 | 20.761 | 23.680 4 | 23.381 6 | 18.883 1 | 20.49 | 23.916 2 |
| 不变矩φ5 | 38.246 0 | 43.665 8 | 47.603 8 | 46.445 8 | 38.368 3 | 42.138 7 | 47.775 9 |
| 不变矩φ6 | 25.998 6 | 27.428 9 | 29.641 0 | 28.280 9 | 25.442 8 | 27.121 4 | 29.960 1 |
| 不变矩φ7 | 39.189 8 | 41.587 8 | 47.632 7 | 47.935 1 | 39.392 3 | 41.143 9 | 49.149 9 |
| 像的熵e | 5.806 6 | 5.384 2 | 6.146 9 | 2.529 6 | 5.795 8 | 5.415 3 | 6.138 3 |
| 面积S | 2 500 | 5 849 | 10 972 | 1 144 | 2 160 | 5 121 | 9 700 |
| 实际距离/mm | 2 763.2 | 2 922.0 | 3 175.0 | 2 822.0 | 2 961.7 | 3 122.0 | 3 373.9 |
| 测量距离/mm | 2 637.5 | 2 910.4 | 3 147.2 | - | 2 837.5 | 3 110.4 | 3 347.2 |
| 测量误差 | 4.547% | 0.397% | 0.786% | - | - | - | - |
图 1(h)是用文献[5]中的算法对图 1(a)处理得到的深度图,图 1(i)是用价格昂贵的双目立体视觉产品Bumblebee获得的右目图像(物距同样为u),图 1(j)则是用该Bumblebee获得与图 1(i)相对应的深度图,灰色区域表示深度不能确定的区域。
图 1(k)是从俯视角度拍摄的便于分辨物体距离相机远近位置的图像,即物体在桌面上的摆放空间位置关系,清晰地显示了各个物体距离相机的远近位置关系。
比较图 1(g)、图 1(h)和图 1(j)三幅深度图,可以看出,图 1(h)是一幅完整的深度图,即其每个像素都表示该位置的深度,但是该深度图中有多处明显错误的地方,如中间的茶叶桶的正面是一个平面,实际深度基本没有差别,但绿色箭头所指的区域却与周围的部分有较大的深度差异;图上蓝色箭头所指的柜门钥匙部位为整幅图片上颜色最淡的,即深度值最大,这显然是不正确的;图中黄色箭头所指的键盘挡板的深度应与其左侧的柜门深度一致,但在该深度图上它们却有明显差异;还有红色箭头所指位置与相机镜头距离很近,但图上该位置的灰度颜色较淡,即深度值较大。图 1(j)中也有大片的深度不能识别的区域,物体边界非常模糊不清,在可识别深度的区域也有明显错误的地方,如两个白色箭头所指处,和白色方框内部区域。而图 1(g)中虽然有大片不能识别深度的白色区域,但其测量出的每个物体深度的精确程度都很高,最大误差不到5%,且物体边界清晰。
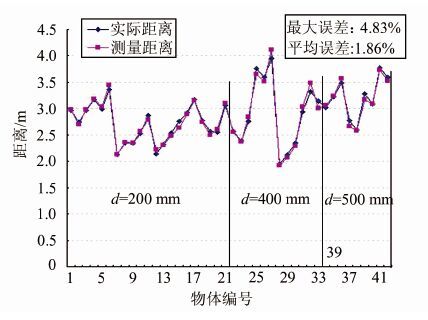
为了更好地验证本文算法的性能,共拍摄了15组图像,含有42个待测距物体,其中第1~7组(第1~21个物体)沿光轴方向的移动距离d=200 mm,第8~11组(第22~33个物体)的d=400 mm,第12~15组(第34~42个物体)的d=500 mm。本文算法能够准确地实现物体匹配,各物体深度的测量结果如图 2所示,其中测量的最大误差为4.83%,平均误差为1.86%。图 3是其中两组图像的实验结果及其与文献[5]算法和立体视觉产品所获得的深度图的对比。
|
| 图 2 物体深度测量结果 Fig. 2 Measuring Results of Objects Depth |
文献[6]也提出采用单目相机采集两幅图像来获取图像的中物体深度。表 5将该方法与本文方法的不同之处和实验结果进行了比较,相对来说本文方法的测量精度稍高些。
在获取每组图像数据时需要沿光轴移动距离d,d的值由相机的场深决定,一般普通相机对准目标物体聚焦拍摄后,再移动距离d≤500 mm时拍摄,则这两次拍摄均在场深范围内,本文实验中d∈[200, 500],另外,由于拍摄角度难控制,很难做到严格沿光轴移动,实际操作时可以将相机安装在可以调节水平的导轨上或比较水平的平台上,使相机的光轴与导轨的移动方向近似重合即可。本文是将相机放在由多张课桌拼接的平台之上近似沿光轴移动的,上述实验结果表明只要相机的移动方向与光轴近似重合,d≥200 mm且两次拍摄均在场深范围内,则测量的深度就比较精确,最大误差在5%以内,平均误差不足2%。
5 结 语本文提出的物体深度测量方法在采集图像时使用普通相机即可,操作简便,不需要对相机做任何改动,也不需要做相机标定、角点匹配等工作。对图像内静态物体深度的测量能够自动完成,无需人工干预,测量精度较高,最大误差小于5%,平均误差仅为2%以内,具有较好的实用价值。
| [1] | Liu Qiong, Yang You, Gao Yue, et al. A Bayesian Framework for Dense Depth Estimation Based on Spatial-Temporal Correlation[J]. Neurocomputing, 2013,104(3):1-9 |
| [2] | Sellent A, Favaro P. Optimized Aperture Shapes for Depth Estimation[J]. Pattern Recognition Letters, 2014,40(4):96-103 |
| [3] | Sun Zhanli, Lam K M, Gao Qingwei. Depth Estimation of Face Images Using the Nonlinear Least-Squares Model[J]. IEEE Transaction on Image Processing, 2013,22(1):17-30 |
| [4] | Pentland A P. A New Sense for Depth of Field[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1987, 9(4):523-531 |
| [5] | Zhou Shaojie, Sim T. Defocus Map Estimation from a Single Image[J]. Pattern Recognition, 2011, 44(9):1852-1858 |
| [6] | Tang Huiming, Hu Zheng, Zhi Chenjiao. Measure Method of Depth, Depth of Field and Object Size Based on Monocular Camera:CN201110007172.8[P]. 2012-11-21(唐慧明,胡铮,支晨蛟.基于单目摄像机的深度、深度场及物体大小的测量方法:CN201110007172.8[P]. 2012-11-21) |
| [7] | Li C M,Kao C,Gore J,et al. Implicit Active Contours Driven by Local Binary Fitting Energy[C]. IEEE Conference on Computer Vision and Pattern Recognition, Minnesota,USA,2007 |
| [8] | Li C M,Kao C,Gore J,et al. Minimization of Region-Scalable Fitting Energy for Image Segmentation[J]. IEEE Transactions on Image Processing,2008,17(10):1940-1949 |
| [9] | Li Aixia,Guan Zequn,Feng Tiantian. A Novel Method on Manifold for Multi-image Matching[J]. Geomatics and Information Science of Wuhan University, 2012, 37(11):1303-1306(李爱霞,关泽群,冯甜甜.一种利用流形学习进行多影像匹配的方法[J]. 武汉大学学报·信息科学版, 2012, 37(11):1303-1306) |
| [10] | He Peipei,Wan Youchuan, Gao Xianjun,et al. Street View Images Matching Algorithm Based on Color Scale-Invariant Feature Transform[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7):867-872(何培培, 万幼川,高贤君,等.基于彩色信息尺度不变特征的街景影像匹配[J].武汉大学学报·信息科学版, 2014,39(7):867-872) |
| [11] | Du Bo, Zhang Liangpei, Li Pingxiang,et al. A Constrained Energy Minimization Method in Subpixel Target Detection Based on Minimization Noise Fraction[J]. Joural of Image and Graphic, 2009,14(9):1850-1857(杜博, 张良培, 李平湘, 等.基于最小噪声分离的约束能量最小化亚像元目标探测方法[J]. 中国图象图形学报, 2009,14(9):1850-1857) |
| [12] | Du Bo, Zhang Lefei, Li Lingxiang,et al. Discrimination Manifold Learning Approach for Hyperspectral Image Dimension Reduction[J]. Acta Photonica Sinica, 2013, 42(3):320-325(杜博, 张乐飞, 张良培, 等. 高光谱图像降维的判别流形学习方法[J]. 光子学报, 2013, 42(3):320-325) |
| [13] | Shi Q, Zhang L, Du B. Semisupervised Discriminative Locally Enhanced Alignment for Hyperspectral Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(9):4800-4815 |
| [14] | Gonzalez R C, Woods R E. Digital Image Processing(Third Edition)[M]. Beijing:Publishing House of Electronics Industry, 2011 |
| [15] | Hu M K. Visual Pattern Recognition by Moment Invariants[J]. IRE Transactions on Information Theory, 1962, 8(2):179-182 |
| [16] | Wang Yaoming. Moment Function on Images:Principles, Algorithms and Applications[M]. Shanghai:East China University of Science and Technology Press, 2002(王耀明.图像的矩函数:原理、算法及应用[M].上海:华东理工大学出版社,2002) |
 2016, Vol. 41
2016, Vol. 41


