文章信息
- 陈建宏, 赵拥军, 赖涛, 刘伟, 黄洁
- CHEN Jianhong, ZHAO Yongjun, LAI Tao, LIU Wei, HUANG Jie
- 单视全极化SAR图像快速非局部均值滤波
- Fast Non-local Means Filtering of SLC Fully PolSAR Image
- 武汉大学学报·信息科学版, 2016, 41(5): 629-634
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 629-634
- http://dx.doi.org/10.13203/j.whugis20140089
-
文章历史
- 收稿日期: 2014-09-14

2. 信息工程大学导航与空天目标工程学院, 河南郑州, 450001
2. School of Navigation and Aerospace Engineering, Information Engineering University, Zhengzhou 450001, China
极化SAR遥感图像提供了更加丰富的目标信息,使其在采集地物电磁散射信息应用中发挥着重要作用。由于极化SAR受相干斑噪声严重干扰,不仅导致数据质量下降,同时给极化SAR数据分类、目标检测等后处理带来困难。抑制相干斑噪声成为极化SAR信息处理中的重要问题。
文献[1]提出的非局部均值(non-local means,NLM)方法[1]近年来受到广泛关注,其基本原理是利用图像块的相似性作为均值滤波的加权权重。该算法对于自然图像的去噪效果非常好,尤其是在边缘、纹理等细节信息的保持方面明显优于其他现有方法。目前该方法已逐步推广到极化SAR图像的相干斑抑制[2, 3, 4, 5, 6]。然而,降低噪声时,一般通过多视来进行预处理,文献[5]研究了多视处理对SAR图像舰船探测的影响,结果表明多视处理提高了等效视数,改善了图像质量,更有利于船只探测;但是多视处理又降低了图像空间分辨率和船只海面对比度,对船只探测产生不利影响。对于其他感兴趣目标,单视条件下SAR图像的空间分辨率最高,强散射点目标比较显著,但相干斑噪声严重破坏了感兴趣目标(面状或者线状)的结构特征。SAR图像多视处理在降低图像斑点噪声的同时降低了空间分辨率,但可增强SAR图像中面状或线状目标的结构特征。因此,需要寻求一种折中的滤波方法来兼顾保持地物的结构特征与空间分辨率。NLM算法的另一难题是计算量大,就极化SAR图像快速滤波而言,仅在文献[3]中提到了采用积分图来快速化,但并未给出具体算法实现。
针对上述问题,本文提出了单视极化SAR的NLM算法。首先,采用多视极化SAR图像求取相似性度量,并用原单视极化SAR图像重构滤波结果。该策略可以充分挖掘多视改善地物结构的特性,同时保持了单视条件下的高分辨特性。求取相似性过程中,结合相干矩阵服从复Wishart分布,分析并选择KL散度作为极化SAR矩阵间相似性度量。然后推导了对称修正Wishart距离展开式,利用积分图在该展开式上实现了极化NLM的快速计算。最后,用实验验证了本文提出算法的滤波效果。
1 极化SAR非局部均值模型相比传统空间域滤波方法,非局部均值使用图块为单元确定权值,突破了基于像素点的滤波设计体系。通过图块的比较提取了图像中的结构信息,从根本上保证了边缘和奇异点的结构不被破坏,进而允许设置非常大的搜索窗口,使图像中均匀区域的噪声能够得到充分的抑制。其滤波形式为[1]:
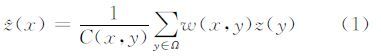
式中, (x)为像素x的滤波结果;w(x,y)为权值函数,由中心像素x和参与估计的像素y所对应图块之间的相似性度量函数D(x,y)决定:
(x)为像素x的滤波结果;w(x,y)为权值函数,由中心像素x和参与估计的像素y所对应图块之间的相似性度量函数D(x,y)决定:
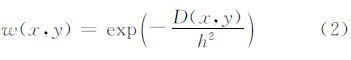
式中,h为滤波参数;C(x,y)=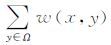 为归一化函数;Ω为像素y的采样区间,称为搜索窗。
为归一化函数;Ω为像素y的采样区间,称为搜索窗。
图块相似性度量由像素x和参与估计的像素y之间的距离d(x,y)获得:
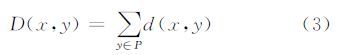
式中,P为像素y的采样区间,称为相似窗。
将式(1)中z(x)、z(y)像素对应为极化相干矩阵X、Y,这样就得到了极化SAR数据的非局部均值模型。本文采用“多视求权、单视重构”思路,将式(1)修正为:
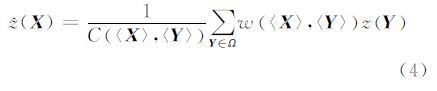
式中,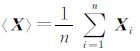 表示X的n视处理。
表示X的n视处理。
非局部均值算法的关键问题是相似程度计算,对于极化SAR,每个散射目标对应的是一个极化相干矩阵,该矩阵包含了雷达测量得到的全部极化信息,因而需要寻找一种可靠计算极化相干矩阵间相似度d(X,Y)的度量函数。
2 基于KL散度的相似测度非局部均值算法的一个重要问题是像素点间的相似性度量。经对比分析各类矩阵相似性测度,本文采用由相对熵推演出的KL距离作为PolSAR协方差矩阵间的相似性度量。在概率和信息论中,KL距离衡量了相同事件空间中两个概率分布的差异情况。满足对称性的KL距离定义为:

式中,I1和I2 为Kullback-Leibler散度,表达如下:
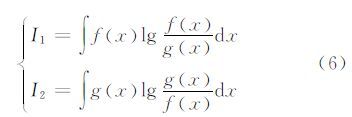
式中,函数f(x)和g(x)分别代表同一分布的两个概率密度函数。如果f(x)=g(x),J=0,表示一个分布与自身的不存在散度。
经过n视处理后,极化SAR相干矩阵服从n自由度的复Wishart分布,T~Wq(n,Σ),相应概率密度函数为:
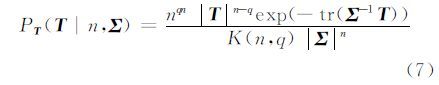
式中,tr表示矩阵的迹;Σ=E(T)为相干矩阵的空间统计平均;满足互易条件下,q=3,是极化相干斑噪声特征矢量的维数。K(n,q)=πq(q-1)/2Γ(n)…Γ(n-q+1),Γ(n)为Gamma函数。
对于极化矩阵X、Y则有
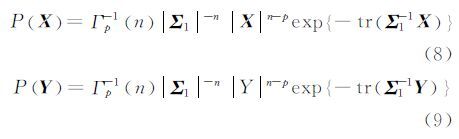
式中,Σ1和 Σ2分别为相干矩阵X、Y的空间统计平均;由此,将式(8)、(9)带入式(5)可得到X与Y之间的KL距离。

详细推导过程见文献[7, 8]。当视数为1时,该距离退化为对称修正复Wishart距离的2倍。
3 快速算法 3.1 积分图与KL距离因式分解任意一点(x0,y0)的积分图>(summed image,SI)值是指从原始图像的左上角到这个点所构成的矩形区域内所有点的灰度值之和。
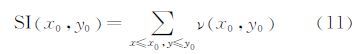
求积分图只需遍历一次原图像,计算开销很小。利用SI可以方便地计算出一个图像块的灰度值累加和。如图 1所示的阴影图像块A的累加和为:
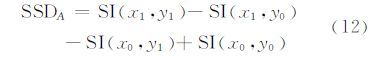
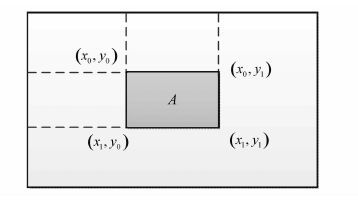
|
| 图 1 利用 SI 计算图像块累加和 Fig. 1 Cumulative of Image Blocks Calculated by SI |
积分图主要是在两方面减少了重复运算,一个是相似性度量的计算次数,还有一个是矩形窗口积分的计算。
在二维图像数据中,像素点间的相似程度可表示为像素灰度差,积分对象就是像素差的二维矩阵。对于极化SAR数据而言,每一个像素扩维成一个3×3的矩阵。矩阵间的相似性需要两个矩阵进行运算,如式(10)所示,这样需要三维的积分图才能满足要求。因此,利用相干矩阵间KL距离的特点,进行因式分解,降维后获得了基于像素点二维积分操作的快速算法。因式分解过程为:
设
则有:
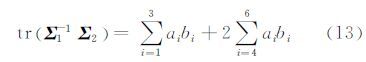
同理tr(Σ2-1 Σ1)也可以得到类似的解析表达式,从而通过矩阵元素的二维积分后再点积来实现式(10)的快速运算。
3.2 算法与性能分析具体实现步骤如下所示。
1) 对T矩阵进行多视与求逆处理,多视结果与逆运算结果分别记为Tm和Tinv。
2) 设置滤波参数搜索窗口Ω大小和相似窗口W大小。
3) 根据Ω与W,对T、Tm和Tinv进行扩展,扩展结果记为Pt、Ptm和Ptinv。
4) 初始化权值w、权值和Σ、最大权值M,对相干矩阵T元素进行滤波。
a) 定义x表示Pt中搜索窗口中心相似性像素,y表示Pt中搜索窗口(dx,dy)位置的非中心相似性像素。
b) 在Ptm中,分别选取所有搜索窗口中心x像素构成的矩阵组A(a1~a6)与所有y对应位置像素构成的矩阵组B(b1~b6)。同理,在Ptinv中对应选取A的逆矩阵组(a′1~a′6)和B的逆矩阵组(b′1~b′6)。先后使用式(13)与式(10)计算像素x与y之间的相似性度量d(x,y)对应图块SD(x,y)。
c) 将SD(x,y)代入式(11)~(12),获得像素x与y为中心的相似性图块间的度量D(x,y),表达为SSD(x,y);将SSD代入式(2)得到滤波权值w(x,y),其中,平滑参数h按照下式计算:
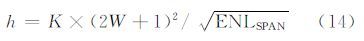
其中,ENLSPAN为极化功率图的等效视数;K为常数,取0.8~1。
d) 用Pt中搜索窗Ω内(dx,dy)位置的像素y对z(x)进行加权滤波,得到像素x的滤波结果,滤波式为:

其中, x为x的滤波结果。
x为x的滤波结果。
e) 更新权值和Σ、最大权值M;
f) 在搜索窗Ω内逐像素进行上述b)~e)处理,得到T整体滤波后的相干矩阵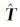 。
。
5) 将T矩阵所有元素T11~T33中的中心像素赋予最大权值M,叠加到滤波结果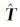 中,并用权值和Σ进行归一化,形成最终滤波结果
中,并用权值和Σ进行归一化,形成最终滤波结果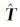 。
。
6) 采用Pauli向量法,使用滤波结果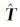 中T11、T22和T33三个元素合成伪彩图。
中T11、T22和T33三个元素合成伪彩图。
由上述分析可知,对于一幅M×M的图像,搜索区域的半径为W,需要M2×(2W+1)2次邻域相似性图块比较,邻域的半径为P,NLM方法计算复杂度为O(9M2×(2W+1)2×(2P+1) 2)。改进后的方法利用积分图计算减少了像点之间相似性重复计算,计算复杂度降为O((2W+1)2×(M+2P+1)2),计算量约为原NLM的(3M×(2P+1))2/(M+2P+1) 2。可见快速算法的计算量要明显小于原NLM,算法效率得到提高。以300×300像素的图像为例,搜索窗10×10像素、相似窗3×3像素条件下计算,运行速度约为原NLM算法的421倍。
4 实验与分析实验环境:Intel (R) Xeon(R) CPU X5670@2.93 GHz CPU,12GB内存,Windows7 64位操作系统。编程工具为MATLAB7.12(R2011a)。
实验图像为2012年Radarsat-2卫星单视全极化SAR图像,分辨率为8 m,选择滤波图像大小为1 500×1 500像素,方位向和距离向采样率分别为4.85 m和4.73 m,成像区域为日本东京湾,图中存在大量舰船目标。Google Earth光学图如图 2(a)所示,其中红色矩形框区域用于后续滤波性能对比。利用Nest软件对实验数据进行辐射校正、地斜校正和正射投影等预处理后,得到了Pauli基合成伪彩色结果,如图 2(b)所示。利用本文算法对整幅图像进行滤波,在实验环境下,运行7 224.99 s后获得检测结果,如图 2(c)所示。

|
| 图 2 Radarsat-2卫星日本东京湾SAR图像滤波结果 Fig. 2 Filtering Results of Radarsat-2 Satellite SAR Image in Tokyo Bay of Japan |
采用的评价指标有等效视数(ENL)、边缘保持指数(ESI)[9]和极化保持能力,其中极化信息保持性能采用Cloude分解结果散射熵H与散射角α来衡量。
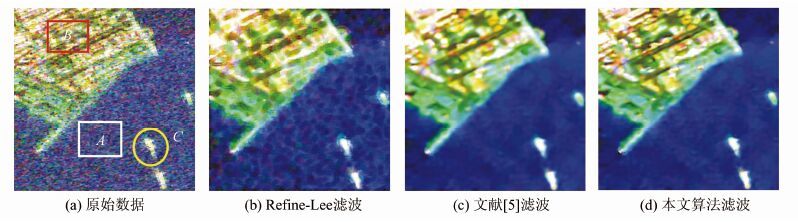
为进一步分析算法的滤波性能,选择图 2红色矩形框内区域数据进行测试,该区域位于港口附近海区域,大小为250×250 像素,区域中有海洋、港口码头、舰船等目标。选取的比较方法是经典的精致极化Lee滤波与文献[5]滤波算法。各算法参数取值为:精致极化Lee滤波的窗口大小取7×7像素,衰减系数D取1;非局部均值和本文算法的搜索窗口大小为21×21像素、相似性窗口大小为7×7像素,平滑参数h取84.648 1。图 3(a)是原始数据Pauli伪彩色图,图 3(b)是精制极化Lee滤波结果,图 3(c)是采用文献[5]距离滤波结果,图 3(d)是本文算法滤波结果。
|
| 图 3 切片图像滤波结果对比 Fig. 3 Contrast Filtering Results of Slice SAR Image |
为便于评价,将极化SAR合成的伪彩色图灰度化,相当于取功率图,然后分别计算图 3(a)中A处海洋同质区域的等效视数ENL,B处码头区域的纹理边缘保持指数EPI,结果见表 1。
对比滤波结果可以发现,图 3(b)中精致Lee滤波平滑效果不理想,整体上出现了人为块状结构,使得边缘比较模糊。在均质海洋区域A对比不同滤波结果可看出,图 3(c)和图 3(d)的滤波结果要明显优于精致极化Lee滤波结果,视觉平滑效果更为清晰。这与表 1中等效视数大小吻合。但是图 3(c)中的平滑过渡,导致模糊了地物的纹理细节。
对比港口码头区域B滤波结果可以看出,精致极化Lee滤波严重模糊了原来码头地物与道路的细节,文献[5]的距离滤波较为清晰,但过度平滑了地物,使得码头上房屋、集装箱与道路之间出现模糊,这主要是由于多视处理而引起的。表 1中B区的边缘保持指数结果反应出本文算法具有较好纹理结构保持能力。
对于海上舰船目标C,精致极化Lee滤波结果不仅出现舰船模糊,而且周边出现扩散杂波。同样,非局部均值滤波结果也出现了较为严重的舰船模糊,放大了目标区域。相比之下,本文算法滤波结果较好地剔除了舰船周边杂波,保持了较清晰的边缘轮廓,更好地反映出目标真实结构与尺寸。
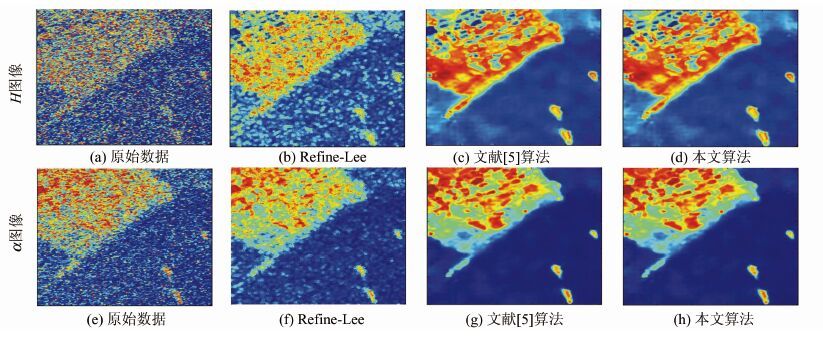
为进一步对比各类算法对极化特征的影响,本文对相干矩阵进行了Cloude分解,利用相应的散射熵H和散射角α来进行分析。各种算法滤波结果进行Cloude分解后的结果如图 4所示,其中图 4(a)~4(d)为对应散射熵图像,图 4(e)~4(h)为对应散射角的图像。对比图 4(a)~4(d)可以看出,在海洋区域内,精致极化lee滤波与文献[5]算法的散射熵出现较多的模糊,效果不理想;文献[5]与本文算法的散射角图像较为一致,均比较清晰。由此看来,本文算法与文献[5]算法保持地物的极化散射特性的性能相当。
|
| 图 4 极化SAR数据Cloude分解结果 Fig. 4 Cloude Decomposition Results of Slice SAR Data |
运算效率方面,从表 1中运行时间可看出,本文算法相比原非局部均值算法,耗费时间从10 745.525 s减小到33.217 s,即由原来的近3 h减小到半分钟,计算速度提高约323倍,极大改善了非局部均值算法在极化SAR中的应用效率。
5 结 语本文针对极化SAR图像相干斑抑制,提出多视求权、单视重构策略并选择KL相似性度量改进了非局部均值模型,运用积分图实现了其快速计算,构建了单视极化SAR图像快速非局部均值算法。实验结果表明,本文算法在一定程度上保持了原图像的空间分辨率,克服了原非局部滤波算法计算量大的缺点。通过定量评估分析可以看出,本文算法较好地实现了对极化SAR图像的滤波,明显增强了相干斑抑制效果。
| [1] | Coll B B, Morel J. A Nonlocal Algorithm for Image Denoising[C]. IEEE Computer Society Conference, San Diego, CA, USA, 2005 |
| [2] | Deledalle C, Denis L, Tupin F. Polarimetric SAR Estimation Based on Non-local Means[C]. IEEE International Symposium, Paris, France, 2010 |
| [3] | Chen Jiong, Chen Yilun, An Wentao, et al.Nonlocal Filtering for Polarimetric SAR Data:A Pretest Approach[J].IEEE Transaction on Geoscience and Remote Sensing, 2011, 49(5):1744-1753 |
| [4] | Wang Shuang,Jiao Licheng, Zhong Hua, et al. Speckle Suppression Method of Polarimetric SAR Data Based on Bayes Non-local Means:10278051[P]. 2011-03-02(王爽, 焦李成, 钟桦,等. 基于贝叶斯非局部均值的极化SAR数据的相干斑抑制方法:10278051[P].2011-03-02) |
| [5] | Yang Xuezhi, Zuo Meixia, Lang Wenhui, et al. Speckle Reduction for Multi-polarimetric SAR Image with the Similarity of the Scattering[J]. Journal of Remote Sensing, 2012, 16(1):105-115(杨学志, 左美霞, 郎文辉,等. 采用散射特征相似性的极化SAR图像相干斑抑制[J].遥感学报, 2012, 16(1):105-115) |
| [6] | Wang Juan,Yang Jinsong,Huang Weigen, et al. The Impact of Multi-look Processing on Synthetic Aperture Radar Ship Detection[J]. Journal of Remote Sensing, 2008,12(3):399-404(王隽, 杨劲松, 黄韦良,等. 多视处理对SAR船只探测的影响[J].遥感学报, 2008, 12(3):399-404) |
| [7] | Lee K Y, Bretschneider T F. Separability Measures of Target Classes for Polarimetric Synthetic Aperture Radar Imagery[J].Asian Journal of Geoinformatics, 2012, 12(2):73-84 |
| [8] | Erten E, Reigber A, Hellwich O, et al. Glacier Velocity Monitoring by Maximum Likelihood Texture Tracking[J]. IEEE Trans Geosci Remote Sens, 2009,47(2):394-405 |
| [9] | Xu Ying, Zhou Yan. Review of SAR Image Speckle Suppression[J]. Computer Engineering and Applications, 2013, 49(20):210-216(徐颖, 周焰. SAR图像相干斑抑制研究进展[J].计算机工程与应用, 2013, 49(20):210-216) |
 2016, Vol. 41
2016, Vol. 41


