文章信息
- 白璘, 刘盼芝, 惠萌
- BAI Lin, LIU Panzhi, HUI Meng
- 利用小波核最小噪声分离进行高光谱影像SVM分类
- SVM Classification of Hyperspectral Image Based on Wavelet Kernel Minimum Noise Fraction
- 武汉大学学报·信息科学版, 2016, 41(5): 624-628,644
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 624-628,644
- http://dx.doi.org/10.13203/j.whugis20140209
-
文章历史
- 收稿日期: 2014-09-22

高光谱成像遥感是近30年来兴起的一种新型对地观测技术。高光谱影像(hyperspectral imagery,HSI)具有丰富的地物光谱信息,在地物识别上优势巨大。如何利用HSI光谱信息高效识别地物是高光谱影像应用研究的核心问题[1, 2, 3]。HSI分类是一种基于特征模型的地物识别方法,它将像元看成是分布在特征空间中的样本,依据各类地物在特征空间中的分布规律进行不同类别地物的分类。HSI分类是面向海量数据的高维相关特征空间中的非线性可分问题[4]。
按照训练过程中是否有训练样本参与,可将HSI分类分为非监督分类与监督分类。非监督分类主要包括K均值聚类、ISODATA 动态聚类、模糊C均值聚类等典型方法[5]。非监督分类没有训练样本,对大样本、高维数据的分类精度不高。在监督分类中,近年来被广泛应用的是最小距离分类、最大似然分类、贝叶斯分类、神经网络分类等。在训练样本集有限的情况下,具有高维相关特征的HSI分类问题会遇到“维数灾难”现象。HSI特征降维方法通常采用主成分分析(principal component analysis,PCA)、无参数加权特征提取(nonparametric weighted feature extraction,NWFE)、最小噪声分离变换等线性特征提取方法,在一定程度上会降低地物类别的可分性。为了满足HSI分类处理对精度、速度和可靠性的要求,有必要针对HSI数据特点研究新的适用于HSI影像分类的理论、模型和算法。
国内外研究人员对非线性特征提取方法进行了大量研究,提出了遗传算法、神经网络、流行学习等方法。核方法是利用核函数将线性分析作非线性推广,核函数是建立在 Hilbert 空间理论基础上的。近年来,有许多学者相继提出了基于核方法的非线性特征提取方法[6, 7, 8],如核主成分分析(kernel principal component analysis,KPCA)[9, 10, 11, 12]、核Fisher判别分析[13]、广义判别分析等。
本文在线性最小噪声分离(minimum noise fraction,MNF)变换的基础上,引入小波核,提出基于小波核最小噪声分离变换(wavelet kernel minimum noise fraction,WKMNF)的非线性特征提取方法。将WKMNF和支持向量机(support vector machine,SVM)相结合,对HSI进行分类,以期得到一种效果较好的HSI分类方法。
1 小波核最小噪声分离变换 1.1 核最小噪声分离变换MNF是一种常见的HSI特征提取方法。假设HSI为n个像素点、r个光谱波段的观测数据集,组成n行r列的矩阵I。假定xTe为原始数据d(l)的线性组合。将d(l)表示为不相关的两部分,即信号部分dS(l)和噪声部分dN(l)之和。原始数据d的方差矩阵C可记为信号分量CS和噪声分量Cn之和。定义噪声分数FS和信噪比SNR如下:

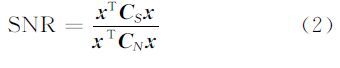
则
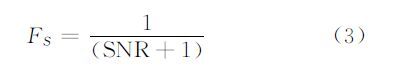
最大化式(4),即为线性MNF变换。
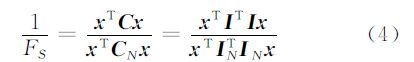
式中,Ⅰ为n×r矩阵;IN是dN(l)的类似定义矩阵。
为使得特征空间的维数对计算不构成直接影响,在设计核函数时需采用对偶表示的形式,这样便不再是显式地表达特征向量而是将数据隐式地表达为特征空间。令x=ITa,则式(4)可重新表示为:
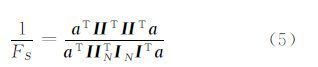
式中,ⅡT矩阵的元素为I的行向量。令U表示I的Hilbert空间映射,UN表示IN的Hilbert空间映射(UN为一个n×p矩阵,其中p≥r),则有核矩阵K=UUT,非对称矩阵KN=UUTN。KN元素为k(Ii,INj),i,j=1,…,n。核矩阵K和KN列平均值为零,则核空间MNF变换数学模型为:
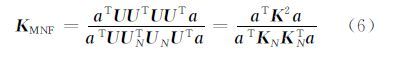
相应地,核空间MNF的求解是通过max(KMNF)来实现的。核最小分离变换的优点主要在于HSI的维数对核矩阵无影响,在计算的时候,只需要在原空间中计算核函数,无需知道非线性映射函数的形式以及非线性变换的结果。
1.2 小波核函数构建核函数主要是为了将HSI的观测数据从一个低维空间投影到另一个高维空间。在这个过程中,某些HSI数据在低维空间中线性不可分的部分,投影到高维空间中则会变成线性近似可分。构建的核函数在通过这种维度投影后一般不能产生一组在该空间上的完备基底,这种基底的不完备性会导致分类器无法在该空间上对任意分类面进行逼近,也不能对任意的分类曲线进行逼近[10]。因此,必须寻找一种新的核函数,使其在新的空间上能够生成一组完备的基底。小波核函数恰恰可以提供这样一种近似的正交基,且小波变换具有多分辨率的特点,可任意地以从粗到细的过程逐步观察HSI数据,提高非线性映射的能力[10, 11]。因此,本文将小波核作为核最小分离变换的核矩阵,构建WKMNF变换。
假设h(x)为一个小波函数,参数α表示伸缩,β表示平移。若存在x,x′∈RN,则有小波核函数的点积形式记为:
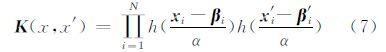
满足平移不变条件下内积核定理表达式为:
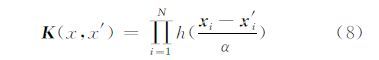
本文选取Morlet函数作为小波变换母函数,根据小波函数平移不变理论构造如下函数:
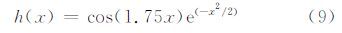
由式(7)~(9)可得到一个满足Mercer核函数要求的小波核函数:
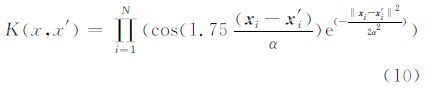
本文将式(10)应用于HSI核最小噪声分离变换,构建了基于小波核的最小噪声分离变换WKMNF。
1.3 基于WKMNF的高光谱影像SVM分类SVM是一种基于统计学习理论的算法。它采用结构风险最小化准则,在最小化样本误差的同时能够缩小模型泛化误差的上界,提高模型的泛化能力。SVM的基本数学模型为[14]:
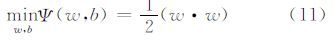
约束条件为:
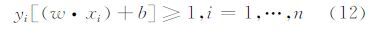
实验数据采用超光谱数字图象收集实验仪器(HYDICE)系统在Washington DC Mall 上空拍摄的HSI。数据大小为1 280×307像素,包含波长范围在400~2 400 nm的220个连续波段,去除被水汽影响的波长在900~1 400 nm范围内的波段,剩余191个波段用于分析。HYDICE高光谱图像波段60、27和17的伪彩色图如图 1所示。该HSI数据包含屋顶、街道、小路、草地、树木、水体以及阴影共7类地物。实验训练数据与测试数据的选取如表 1所示。

|
| 图 1 HYDICE系统拍摄的伪彩色图 Fig. 1 False Color Images of HYDICE |
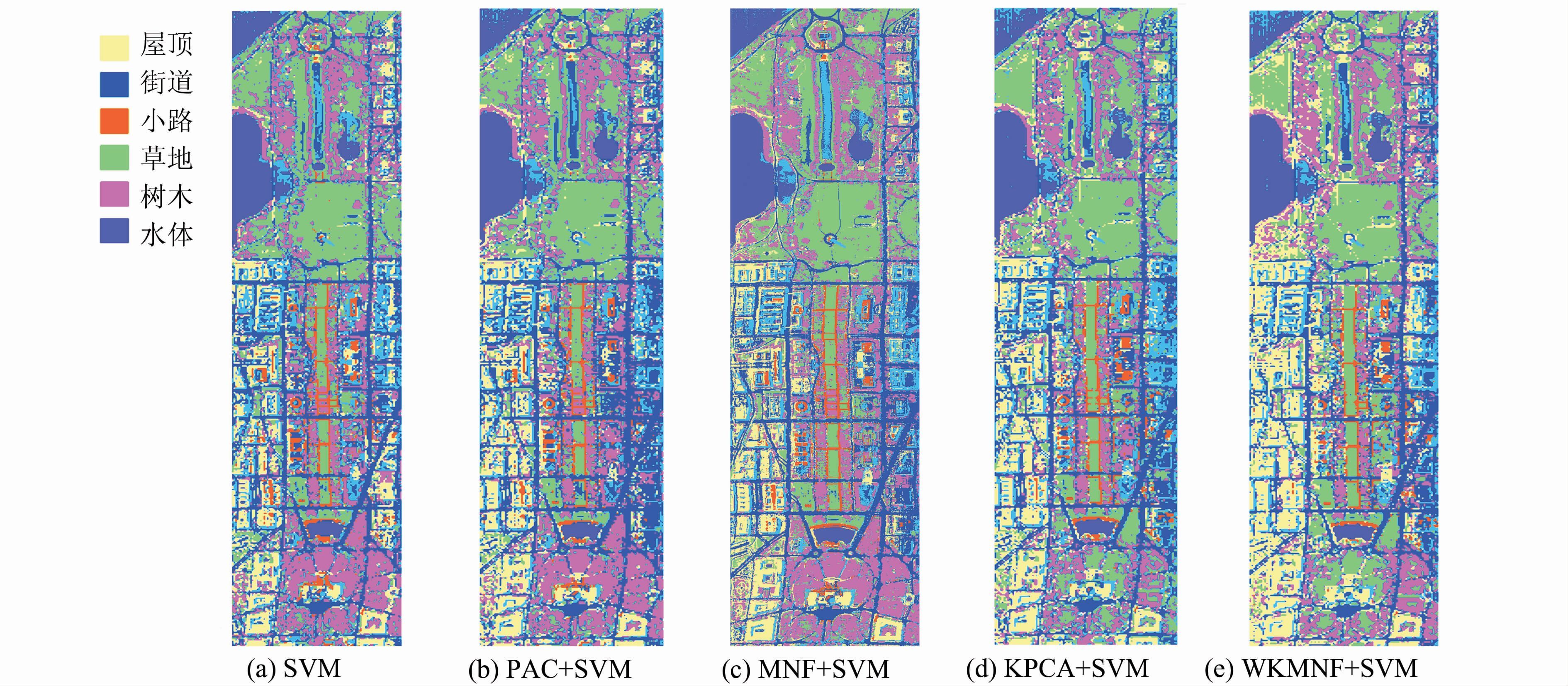
实验将本文提出的WKMNF+SVM方法分别与普通的SVM、PCA+SVM、MNF +SVM、KPCA(高斯核)+ SVM方法做比较。结果采用总体分类精度(overall accuracy,OA)和Kappa系数作为评价标准,重复10次实验,取统计平均作为最终实验结果,如表 2所示,图 2为分类结果图。
| HYDICE数据(Washington DC Mall) | |||
| 类别 | 样本 | ||
| 类号 | 类名 | 训练 | 测试 |
| 1 | 屋顶 | 400 | 3 434 |
| 2 | 街道 | 168 | 248 |
| 3 | 小路 | 36 | 139 |
| 4 | 草地 | 814 | 1 114 |
| 5 | 树木 | 80 | 325 |
| 6 | 水体 | 224 | 1 000 |
| 7 | 阴影 | 11 | 86 |
| 类别 | 类名 | 分类精度 | |||||
| SVM | PCA+SVM | MNF+SVM | KPCA+SVM | WKMNF +SVM | |||
| 1 | 屋顶 | 62.1% | 64.8% | 66.4% | 70.7% | 77.4% | |
| 2 | 街道 | 98% | 100% | 94.8% | 98.4% | 97.6% | |
| 3 | 小路 | 100% | 100% | 100% | 100% | 100% | |
| 4 | 草地 | 97.2% | 98.1% | 97.7% | 100% | 99.8% | |
| 5 | 树木 | 98.8% | 98.8% | 98.8% | 95.4% | 96.8% | |
| 6 | 水体 | 99.9% | 99.9% | 99.9% | 99.8% | 99.8% | |
| 7 | 阴影 | 82.6% | 79.1% | 84.9% | 89.5% | 89.5% | |
| 总体分类精度(OA) | 78.6% | 80.7% | 81% | 84.1% | 87.5% | ||
| Kappa系数 | 0.717 | 0.744 | 0.745 | 0.787 | 0.823 | ||
|
| 图 2 不同方法得到的分类结果图 (HYDICE) Fig. 2 Classification Result Image with Different Methods (HYDICE) |
在SVM进行分类实验前,采用特征提取算法,特征维数取前15个特征分量作为输入,其能量占总量的比重超过96%。可以看出,采用本文提出的WKMNF方法处理后的高光谱图像数据在分类精度上较对比算法有了明显的提升,与高斯核KPCA算法相比,提升幅度超过3%,可较明显地区分地物。
2.2 AVIRIS数据实验为验证算法在不同数据集下的性能,本文选用美国机载可见光/红外成像光谱仪(airborne visible infra-red imaging spectrometer,AVIRIS)扫描仪1992年6月12日在Indiana遥感实验区所获得的220波段高光谱数据进行实验,涵盖波长范围0.4~2.5 um,包含可见光与近红外区域。图像尺寸为145×145像素,图像位数16 bit。该测试数据集包含16个类别:苜蓿地,玉米已耕地,玉米略耕地,玉米未耕地,牧草地,草树地,牧草已割地,干草地,燕麦地,大豆已耕地,大豆略耕地,大豆未耕地,小麦地,林地,建筑物、牧草和汽车的混合地带,塔楼。测试数据集的伪彩色图(30、60、140波段)如图 3所示。实验中每类地物的训练样本数与测试样本数如表 3所示。

|
| 图 3 AVIRIS拍摄的伪彩色图 Fig. 3 False Color Images of AVIRIS |
| 类号 | 地物类型 | 训练样本数 | 测试样本数 | 类号 | 地物类型 | 训练样本数 | 测试样本数 |
| 1 | 苜蓿地 | 27 | 27 | 9 | 燕麦地 | 10 | 10 |
| 2 | 玉米未耕地 | 100 | 1 334 | 10 | 大豆未耕地 | 100 | 2 368 |
| 3 | 玉米略耕地 | 84 | 750 | 11 | 大豆略耕地 | 97 | 871 |
| 4 | 玉米已耕地 | 117 | 117 | 12 | 大豆已耕地 | 62 | 552 |
| 5 | 牧草地 | 50 | 447 | 13 | 小麦地 | 38 | 342 |
| 6 | 草树地 | 75 | 672 | 14 | 林地 | 106 | 106 |
| 7 | 牧草已割地 | 13 | 13 | 15 | 牧草和汽车的混合地带 | 100 | 1 194 |
| 8 | 干草地 | 49 | 440 | 16 | 塔楼 | 48 | 47 |
在AVIRIS数据集上的分类实验是将WKMNF+SVM方法分别与SVM、PCA+SVM、MNF +SVM、KPCA(高斯核)+ SVM方法做比较。结果采用总体分类精度和Kappa系数作为评价标准,重复10次实验,取统计平均作为最终实验结果,如表 4所示,图 4为实验所取得的分类图。其余实验条件与§2.1表述相同。可以看出,采用本文提出的WKMNF方法处理后的AVIRIS数据在分类精度上较对比算法有了明显的提升,较KPCA算法提升幅度超过6%,可较明显地区分地物。

|
| 图 4 不同方法得到的分类结果图 (AVIRIS) Fig. 4 Classification Result Image with Different Methods (HYDICE) |
从§2.1与§2.2的实验中可以看出,无论是在HYDICE数据集还是在AVIRIS数据集上进行的分类实验,本文提出的WKMNF+SVM的方法都能获得良好的分类精度。这主要是由于WKMNF方法充分利用了高光谱影像数据中的非线性特点,实验结果要好于采用线性方法或高斯核函数的非线性方法。
3 结 语面对高光谱遥感影像的特点和现有数据预处理方法的不足,本文提出了一种采用小波核最小噪声分离变换(WKMNF)结合SVM的分类方法对HIS进行分类。在HYDICE数据集以及AVIRIS数据集上的实验表明,WKMNF算法对数据与预处理和特征提取的能力强于对照实验中的算法,将最终处理后的数据应用于支持向量机的高光谱影像分类中,分类精度可提高3%~9%,证明了本文算法的有效性。
| [1] | Wang Yiting, Huang Shiqi, Liu Daizhi, et al. Research Advance on Band Selection-Based Dimension Reduction of Hyperspectral Remote Sensing Images[J]. Remote Sensing, Environment and Transportation Engineering,2012(1):1-4 |
| [2] | Dopido I, Villa A, Plaza A, et al. A Quantitative and Comparative Assessment of Unmixing-Based Feature Extraction Techniques for Hyperspectral Image Classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(2):421-435 |
| [3] | Goetz A F H. Three Decades of Hyperspectral Remote Sensing of the Earth:A Personal View[J]. Remote Sensing of Environment, 2009, 113(1):5-16 |
| [4] | Plaza A. Recent Advances in Techniques for Hyperspectral Image Processing[J]. Remote Sensing of Environment, 2009, 113(1):110-122 |
| [5] | Bioucas-Dias J M, Plaza A, Camps-Valls G, et al. Hyperspectral Remote Sensing Data Analysis and Future Challenges[J]. Geoscience and Remote Sensing Magazine, 2013(2):6-36 |
| [6] | Hosseini S A, Ghassemian H. A New Fast Algorithm for Multiclass Hyperspectral Image Classification with SVM[J]. International Journal of Remote Sensing, 2011, 32(23):8657-8683 |
| [7] | Fauvel M, Chanussot J, Benediktsson J A. A Spatial spectral Kernel Based Approach for the Classification of Remote sensing Images[J]. Pattern Recognition, 2012,45:381-392 |
| [8] | Chen Yi, Nasser M, Trac D T. Hyperspectral Image Classification via Kernel Sparse Representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013,51(1):217-231 |
| [9] | Lin Na, Yang Wunian, Wang Bin. Hyperspecral Image Feature Extraction via Kernel Minimum Noise Fraction Transform[J]. Geomatics and Information Science of Wuhan University,2013,38(8):988-992(林娜,杨武年,王斌. 高光谱遥感影像核最小噪声分离变换特征提取[J]. 武汉大学学报\5信息科学版,2013,38(8):988-992) |
| [10] | Zhao Chunhui, Zhang Yi, Wang Yulei. Relevant Vector Machine Classification of Hyperspectral Image Based on Wavelet Kernel Principal Component Analysis[J]. Journal of Electronics & Information Technology, 2012,34(8):1905-1910(赵春晖,张焱,王玉磊. 基于小波核主成分分析的相关向量机高光谱图像分类[J]. 电子与信息学报,2012,34(8):1905-1910) |
| [11] | Wu Fangfang, Zhao Yinliang. Novel Reduced Support Vector Machine on Morlet Wavelet Kernel Function[J]. Control and Decision, 2006,21(8):848-856(武方方,赵银亮. 一种基于Morlet小波核的约简支持向量机[J]. 控制与决策, 2006, 21(8):848-856) |
| [12] | Wan Jiaqiang, Wang Yue, Liu Yu. Improvement of KPCA on Feature Extraction of Classification Data[J]. Computer Engineering and Design, 2010,31(18):4085-4088(万家强,王越,刘羽.改进KPCA对分类数据的特征提取[J]. 计算机工程与设计,2010,31(18):4085-4088) |
| [13] | Yang Guopeng, Yu Xuchu, Zhou Xin, et al. Hyperspectral Image Feature Extraction Based on Generalized Discriminant Analysis[J].Journal of Dalian Maritime University, 2008,34(8):59-63(杨国鹏,余旭初,周欣,等.基于广义判别分析的高光谱影像特征提取[J].大连海事大学学报,2008,34(3):59-63) |
| [14] | Chen J, Wang C,Wang R. Using Stacked Generalization to Combine SVMs in Magnitude and Shape Feature Spaces for Classification of Hyperspectral Date[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(7):2193-2205 |
 2016, Vol. 41
2016, Vol. 41



