文章信息
- 张艳, 王涛, 冯伍法, 王淑香
- ZHANG Yan, WANG Tao, FENG Wufa, WANG Shuxiang
- “天绘一号”海岛(礁)影像稀少控制下的定位技术研究
- Positioning Technology Study for Mapping Satellite-1 Islands (Reefs) Imagery with Scarce Controls
- 武汉大学学报·信息科学版, 2016, 41(5): 617-623
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 617-623
- http://dx.doi.org/10.13203/j.whugis20140220
-
文章历史
- 收稿日期: 2014-09-18

我国海岛(礁)分布零散,现有大地控制网海面延伸能力不足,地面特征不明显,遥感影像落水范围大,外业控制测量工作成本高、劳动强度大、风险系数高,在待定位的海岛(礁)卫星影像上难以获得满足数量和分布要求的地面控制点。常规的遥感影像定位方法不但对地面控制点的数量有一定要求,而且对地面控制点分布的要求也很高。为此需要研究如何实现稀少控制或无控制条件下的卫星影像定位,达到海岛(礁)几何信息获取精度要求,而目前针对海岛(礁)卫星影像的定位还缺乏深入的研究。文献[1]提出利用一种基于海岸线配准的几何校正方法,但海岸线提取本身就不稳定,而且海图中海岸线现势性较差,所以基于这两者配准的卫星影像定位精度很受局限。文献[2]研究利用ADS40相机实现海岛(礁)区域的大比例尺成图,这种测图方式需要专门的飞行计划,而且对于基站布设和航线规划要求很严格,实时性和普遍应用性不强。
“天绘一号”(TH-1)卫星是我国第一颗传输型立体测绘遥感卫星,本文以TH-1卫星01A级影像为研究对象,针对如何实现稀少控制或无控制条件下海岛(礁)区域卫星影像的定位展开研究。海岛(礁)卫星影像定位的困难在于缺乏地面控制,TH-1三线阵CCD影像具备完备的定轨测姿数据,但是原始的01A级数据精度还难以满足高精度无控定位需求。本文首先构建了TH-1卫星影像的严格成像模型,然后分析了TH-1卫星影像定位误差的主要来源,提出通过自检校区域网平差技术改正各项主要系统误差,提高定轨测姿数据的精度,最后利用基于轨道外推的定位技术实现无控制和稀少控制条件下的海岛(礁)卫星影像定位。
1 TH-1三线阵CCD影像严格成像模型
根据卫星和传感器的前期设计,并结合定轨测姿和实验室标定数据,得到TH-1卫星三线阵CCD影像的严格几何处理模型为:

模型(1)涉及到前/下/后视的独立像空间坐标系、传感器坐标系和CGCS2000国家大地坐标系[3]。前/下/后视独立像空间坐标系的原点是各自的投影中心,x轴沿飞行方向,y轴沿CCD扫描方向。传感器坐标系原点在下视投影中心,Y轴平行于扫描行方向,X轴垂直于扫描行指向线阵列推扫方向,Z轴按照右手规则确定。CGCS2000大地坐标系原点为包括海洋和大气的整个地球的质心,GCS2000椭球与WGS84椭球可以认为是一致的。(0,y′+dy,-f)为像点在像空间坐标系下的坐标,其中dy为CCD线阵上探元在y方向的偏移误差,实验室共标定了线阵上30个探元的偏移误差,对于每一探元上的误差利用三次样条函数内插得到;Rδ为CCD在焦平面的旋转角所构成的旋转矩阵;RΦ为前视相机、后视相机相对于下视相机的夹角所构成的旋转矩阵;像点向量[0y′+dy-f]T乘以矩阵Rδ和RΦ,在考虑CCD旋转影响后,由各视独立的像空间坐标系转换到传感器坐标系。RSensorCGCS2000为相机成像时刻传感器坐标系相对于CGCS2000坐标系的旋转角构成的旋转矩阵,由精密定姿数据确定;λ为比例系数;传感器坐标系下的坐标值乘以RSensorCGCS2000和λ,完成物空间坐标系CGCS2000的转换。(XSt,YSt,ZSt)为相机成像时刻投影中心在CGCS2000坐标系下的位置,可以由精密定轨数据确定。
合并严格几何处理模型(1)中矩阵R(δ)和坐标向量0y′+dy-fT得到像点坐标向量xy-fT。RΦ由前/后视交会角确定,参照SPOT和资源3号卫星的研究报告[4],并结合TH-1卫星的多组实验数据,确定旋转矩阵RΦ的具体形式为 。将RΦ代入式(1),得到:
。将RΦ代入式(1),得到:
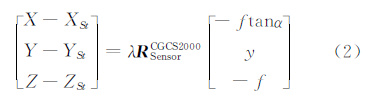
将式(2)写成共线条件方程形式,就是最终建立的TH-1卫星三线阵影像严格成像模型。
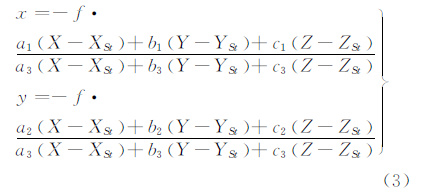
式中,ai、bi、ci(i=1,2,3)为矩阵RSensorCGCS2000中外方位角元素φ、ω、κ构成的函数;x=-ftanα。
2 基于轨道外推的TH-1影像定位基于轨道外推的卫星影像定位技术的基本思想就是在卫星轨道运行平稳的前提下,利用控制条件丰富的境内检校场等实验数据,对卫星影像进行标定处理,消除存在于定姿和测轨数据、焦距、前后视交会角中的系统误差;然后利用标定后的定姿和测轨参数,外推获得沿海区域海岛(礁)卫星图像的定姿和测轨参数,实现无控制条件下的海岛(礁)图像高精度定位。
TH-1卫星三线阵CCD影像属于行中心投影影像,三线阵CCD传感器在成像时,不同扫描线对应的摄影中心位置和姿态都不一样,区域网平差时外方位元素个数大于观测值个数,无法解算每一条扫描线的外方位元素,因此需要采用合适的数学模型模拟卫星轨道。目前常用的轨道模型有线性多项式模型、分段多项式模型和定向片模型[4]。对于长条带的三线阵CCD影像,分段多项式模型和定向片模型最为合适。如果条带长度适中,分段多项式模型可以满足需求。本文采用分段多项式建立卫星轨道模型,每景影像建立一组外方位元素模型。
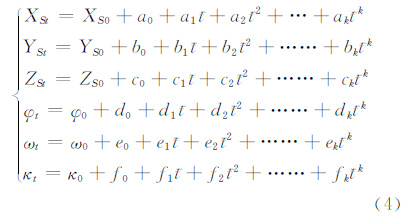
式中,t0为影像中心扫描行成像时刻,t=t-t0; (XS0,YS0,ZS0,φ0,ω0,κ0)为t时刻外方位元素初始观测值,由姿轨观测数据直接转化而来;(XSt,YSt,ZSt,φt,ωt,κt)为t时刻的外方位元素精确值;ai、bi、ci、di、ei、fi(i=0,…,k)为外方位元素模型参数。
目前,关于各类高分辨率遥感卫星的研究表明定轨技术测定的外方位线元素总体精度非常高,仅带有少量系统误差,影响较小;而姿态角由于测定难度大,误差源多,是影响定位精度的主要误差源[5]。文献[6, 7]曾对SPOT5、Quickbird、资源二号影像的姿态角常差进行了研究。文献[8]也指出TH-1卫星搭载的是高精度GPS定位系统和中等精度定姿系统。因此,由姿态观测数据转换得到的外方位角元素(φ,ω,κ)构成的旋转矩阵RSensorCGCS2000存在不可忽视的误差,误差来源于(φ,ω,κ)的测定。此外,卫星在轨运行过程中,传感器几何成像参数,如焦距和前/后视相机交会角都会发生变化。中国返回式摄影测量卫星经验证实,相机在空间运转过程中焦距变化量最大达到20 μm左右[5]。
经过综合分析,确定影响TH-1卫星几何定位精度的主要参数包括姿态观测数据转换得到的外方位角元素(φ,ω,κ),前/下/后3视相机的焦距fl、fn、fr,前视相机与下视相机的交会角αl,后视相机与下视相机的交会角αr,以及y坐标的主点偏移y0。考虑以上待平差参数,将严格成像模型(3)线性化后,得到线性化的共线条件方程为:
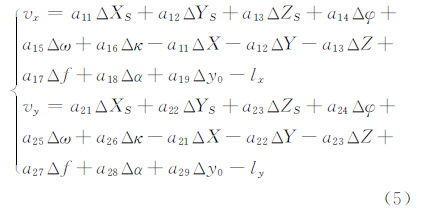
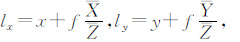
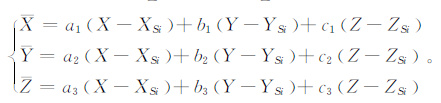
系数a11~a16、a17、a19和a21~a26、a27、a29的推导可参阅文献[9];其余系数推导得到a18=fsec2α,a28=0;Δf、Δα、Δy0也称为相机的标定参数。
式(5)为像点观测方程,因为相机标定参数实际值总是很小,所以还需增加标定参数的虚拟误差方程,则轨道外推技术采用的自检校区域网平差模型可表示为:
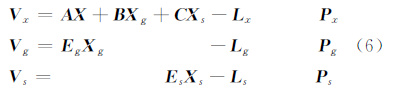
式中,Vx、Vg、Vs表示像点控制点、附加参数观测方程的误差向量;Eg是控制点观测方程的单位系数矩阵;Es是附加参数的单位系数矩阵;X为外方位元素改正数矢量;A为相应的系数矩阵;Lx为像点坐标观测值残差向量;Px为像点观测值权矩阵;Xg为控制点坐标的改正数矢量;B为相应的系数矩阵;Lg为控制点坐标观测值残差向量;Pg为控制点坐标的权矩阵;Xs为标定参数矢量;C为相应的系数矩阵;Ls为附加参数的观测值残差向量;Ps为附加参数的权矩阵。确定Lx、Lg、Ls和权值Px、Pg、Ps可参阅文献 [10]。
建立卫星轨道模型(4)和自检校区域网平差模型(6)后,设计基于轨道外推的TH-1卫星影像无控定位实现方案如下:
1) 利用控制条件丰富的境内检校场等实验数据,采用自检校区域网平差模型(6)对卫星影像进行标定处理,获得标定后的定姿和测轨数据、焦距、前后视交会角和y坐标的主点偏移y0,因为定轨数据精度很高,所以标定过程中可以不考虑外方位线元素误差,只考虑角元素φ,ω,κ误差。
2) 根据轨道平滑条件,对标定后的定姿和测轨参数进行参数内插,外推获得沿海区域海岛(礁)卫星图像的定姿和测轨参数,实现无控制条件下的海岛(礁)图像高精度定位,轨道内插可以采用Lagrange插值算法。
3 实验结果 3.1 实验数据实验采用了两组实验数据,第一组实验数据是河南登封嵩山实验场区域的TH-1卫星01A级影像,第二组数据是浙江舟山区域的TH-1卫星01A级影像。01A级影像仅经过辐射校正,没有进行严格几何校正。嵩山区域数据用于标定TH-1卫星的测轨定姿参数、三视相机的焦距、前/后视相机的交会角和主点偏移y0。舟山区域海岛(礁)影像则用于验证稀少控制条件下或无控制条件下基于轨道外推的卫星影像定位技术的可行性,并检验其精度。
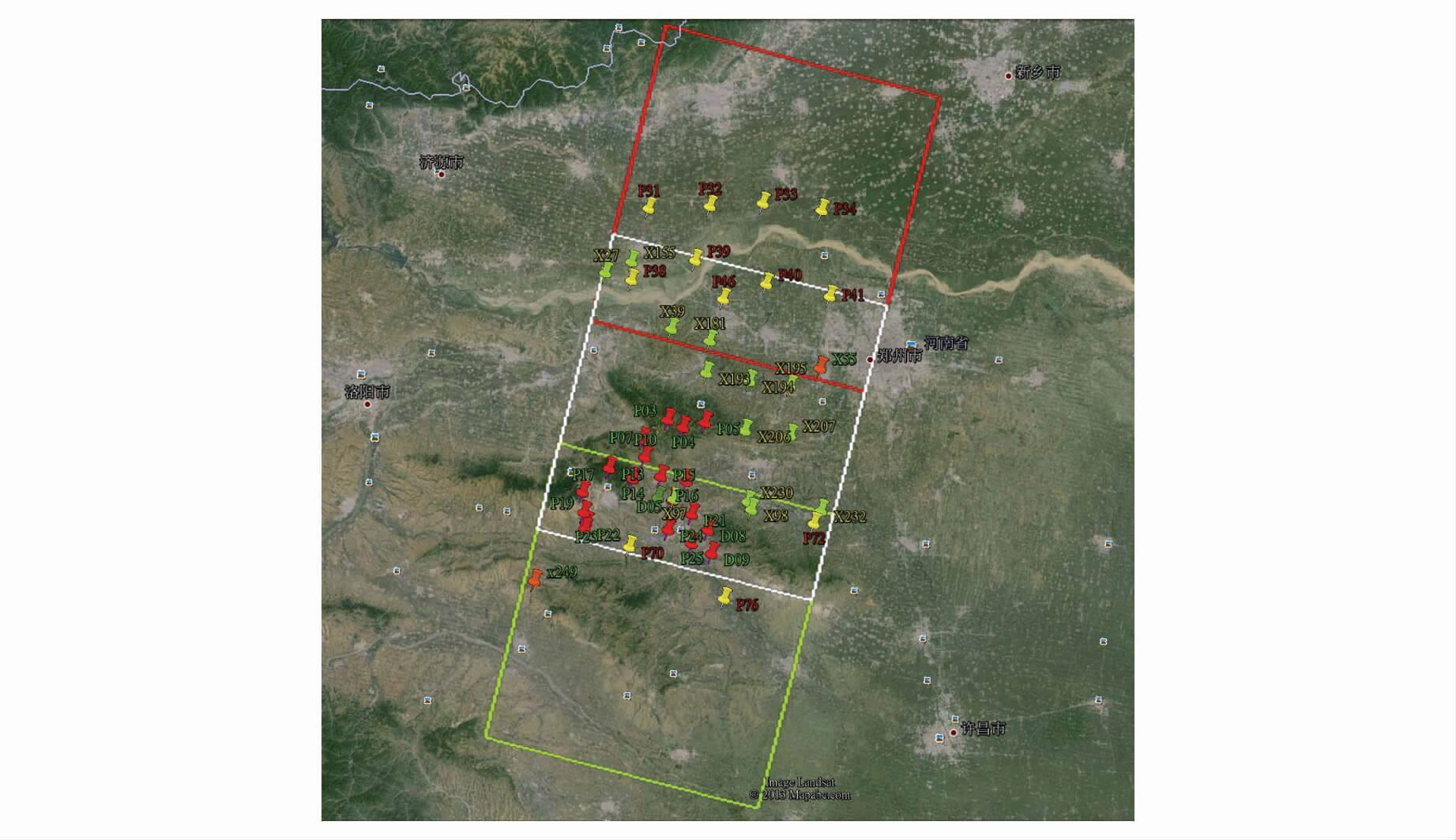
嵩山遥感综合实验场选址在河南登封嵩山地区,该地区主要地貌类别齐全,涵盖有平原、丘陵地、山地等,地形起伏较大,海拔高度约在100 m~1 500 m之间。实验场包括航空定标实验场、摄影测量与遥感综合实验场和航天定标实验场三个部分。航空定标实验场主要用于各种航空相机或传感器的鉴定,摄影测量与遥感综合实验场主要是用于摄影测量与遥感技术综合实验,而航天定标实验场主要是用于各种航天传感器的检校与测试。航空定标实验场内采用控制点埋石方式分级布设了214 个永久性高精度控制点,航天定标实验场目前面积约8 000 km2,实验场内布设69个高精度控制点,以自然、人工地物为标志,平面精度为0.1 m,高程精度为0.2 m。第一组TH-1卫星影像覆盖嵩山遥感综合实验场,可利用实验场数据进行严格的自检校定标处理。影像获取于2010年12月,具备1条轨道数据,轨道标号005,轨道上存在三景影像可用,每景影像具备前/下/后3视。图 1为影像覆盖测区及控制点分布图,其中红色框表示影像005_134,影像覆盖区域内分布14个控制点,白色框表示影像005_135,分布38个控制点,绿色框表示影像005_136,分布19个控制点。像点坐标人工量测精度约为0.5~1个像元。
|
| 图 1 登封区域TH-1图像几何关系及控制点分布 Fig. 1 Geometric Relationship of TH-1 Images over Dengfeng Area and GCP Distribution |
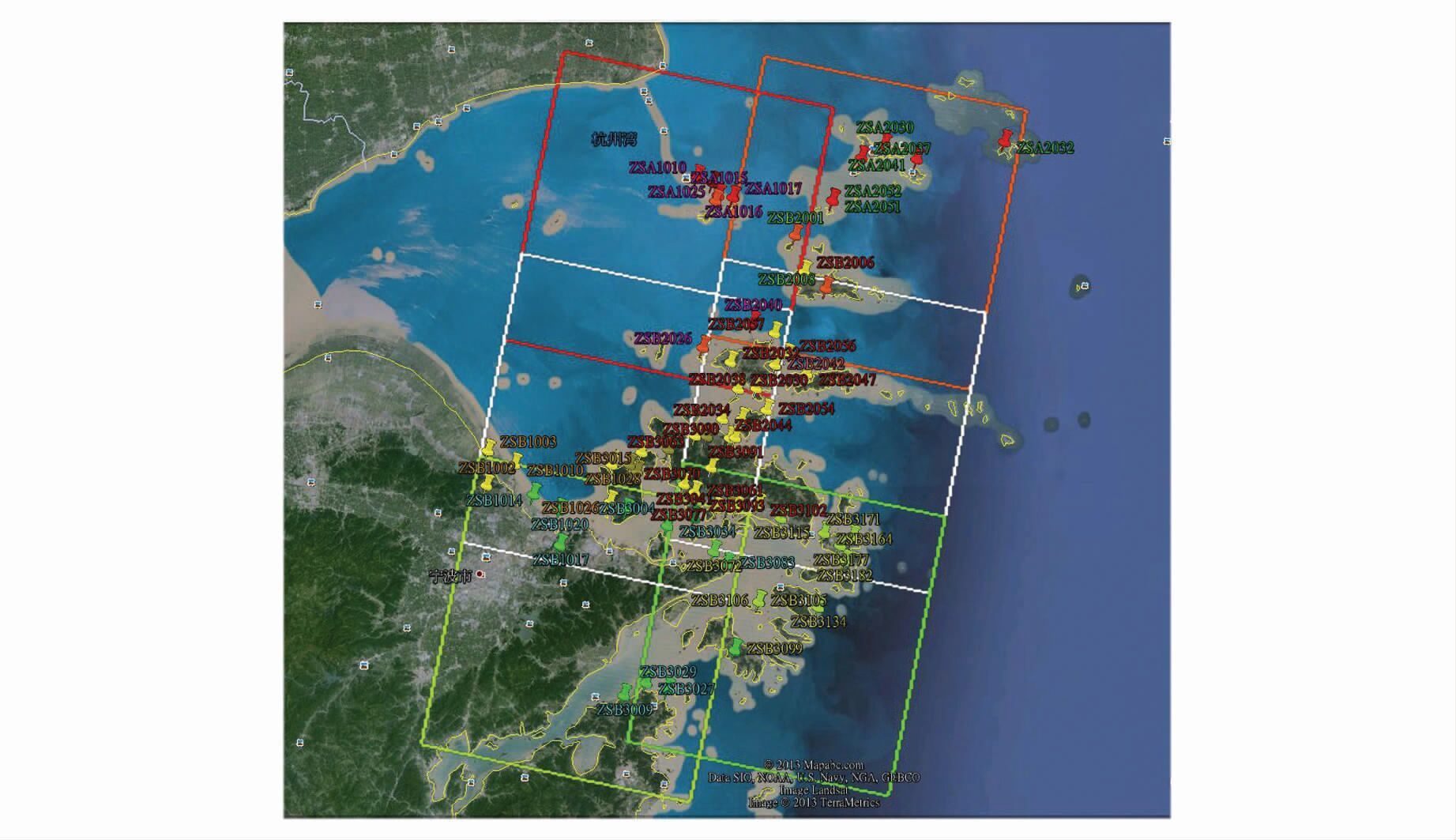
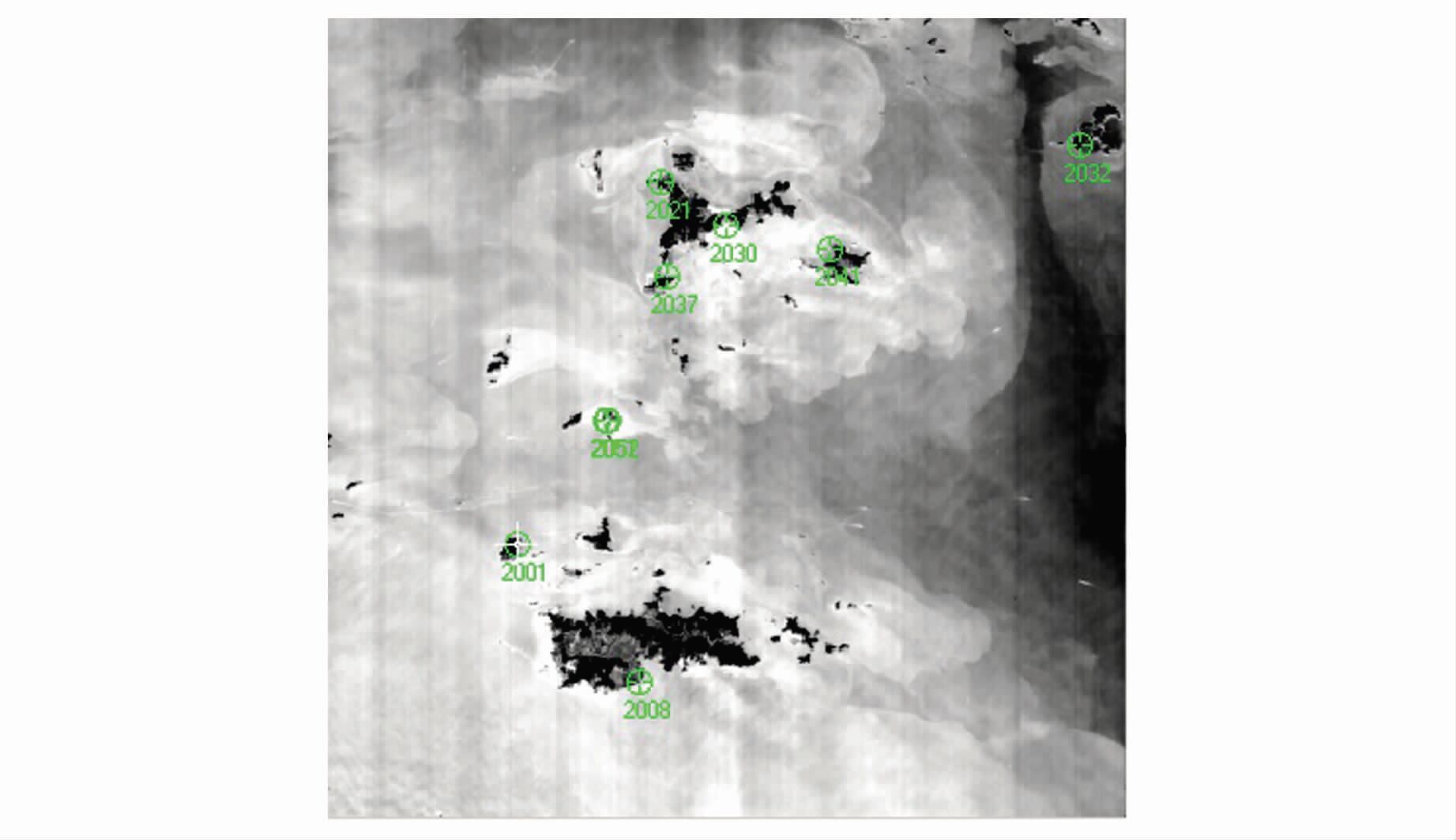
舟山区域TH-1卫星影像具备2根轨道上的6景影像,每景影像具备前/下/后3视,整个区域影像分布关系和控制点分布见图 2。近海轨道标记为863,从北向南影像序号依次为863_145、863_146、863_147。近岸轨道标记为864轨道,从北向南影像序号依次为864_145、864_146、864_147。控制点采用GPS测量,点位精度优于±1 m。其中863_145和864_145景影像覆盖区域几乎全是水域,控制点极为稀少(图 3和图 4)。
|
| 图 2 舟山区域TH-1图像几何关系及控制点分布 Fig. 2 Geometric Relationship of TH-1 Images over Zhoushan Area and GCP Distribution |
|
| 图 3 TH-1图像863_145及控制点分布 Fig. 3 TH-1 Image 863_145 and GCP Distribution |

|
| 图 4 TH-1图像864_145及控制点分布 Fig. 4 TH-1 Image 864_145 and GCP Distribution |
实验内容包括三个部分: (1) 利用嵩山实验场数据和TH-1卫星01A级卫星影像进行几何标定,获得标定参数; (2) 用标定参数对舟山区域的6景01A级海岛(礁)影像进行无控制定位和稀少控制定位; (3) 选取控制点分布较多的2景01A级海岛(礁)影像进行不同控制点条件下的定位研究,并将其精度与无控定位和稀少控制定位精度进行比较。
1) 嵩山区域01A级TH-1影像实验结果。 采用嵩山区域的3景01A级卫星影像,利用自检校区域平差模型(6)进行标定处理,标定参数为定姿参数——角元素φ,ω,κ、前视相机焦距fl、下视相机焦距fn、后视相机焦距fb、前视和下视相机的交会角αl、后视和下视相机的交会角αr、前视CCD的主点偏移yl0和后视CCD的主点偏移yr0,共10个标定参数。
2) 舟山区域01A级TH-1卫星影像基于轨道外推的定位精度。 首先利用附属的星历参数文件,对舟山区域的6景01A级TH-1卫星影像进行直接定位实验;然后利用表 1中的标定参数平均值对舟山区域的轨道参数进行更新和外推,得到6景影像对应的新星历参数,利用新星历参数进行无控定位,利用各景影像上采集的控制点作为检查点,衡量无控定位的精度;最后以新星历参数作为外方位元素初始值,在轨道外推的基础上,进行再次平差,以检查点衡量稀少控制的定位精度。
863_145景卫星图像上分布9个控制点,863_146上分布25个控制点,863_147上分布12个控制点,864_145上分布12个控制点,864_146上分布24个控制点,864_147上分布11个控制点。稀少控制条件下,再次平差时,仅考虑角元素误差,所以只需要选取1个同时分布在3视上的控制点就可以完成平差,其他控制点作为检查点。实验结果见表 2,其中第一列为直接定位精度,第二列为基于轨道外推的无控定位精度,第三列为稀少控制下基于轨道外推再次平差的定位精度。
| 影像 | φ/(″) | ω/(″) | κ/(″) | fl/um | fn/ um | fb/ um | αl/(″) | αr/(″) |
| 005_134 | -22.90 | -68.21 | -25.63 | 2 | -1 | 2 | 10.20 | 8.76 |
| 005_135 | -23.42 | -67.97 | -26.52 | 2 | -2 | 1 | 11.11 | 11.78 |
| 005_136 | -21.98 | -66.74 | -24.01 | 1 | -1 | 0 | 9.45 | 10.13 |
| 平均值 | -22.76 | -67.64 | -25.38 | 1.66 | -1.33 | 1 | 10.25 | 10.22 |
| 影像 | 直接定位均方根误差 | 无控定位均方根误差 | 稀少控制均方根误差 | ||||||
| X | Y | Z | X | Y | Z | X | Y | Z | |
| 863_145 | 200.82 | 64.16 | 29.81 | 13.14 | 12.21 | 10.30 | 10.62 | 9.08 | 8.24 |
| 863_146 | 199.05 | 37.37 | 69.75 | 13.23 | 12.12 | 12.22 | 11.71 | 10.01 | 9.01 |
| 863_147 | 192.98 | 23.05 | 46.40 | 11.41 | 11.29 | 10.09 | 10.02 | 9.72 | 8.88 |
| 864_145 | 206.75 | 10.13 | 52.83 | 10.21 | 9.26 | 10.17 | 8.06 | 7.50 | 6.60 |
| 864_146 | 207.25 | 28.06 | 69.98 | 11.19 | 10.35 | 11.23 | 9.78 | 8.21 | 7.58 |
| 864_147 | 205.25 | 18.77 | 62.48 | 10.25 | 7.64 | 8.04 | 9.39 | 5.11 | 5.25 |
| 平均值 | 202.02 | 30.26 | 55.21 | 11.57 | 10.48 | 10.34 | 9.93 | 8.27 | 7.59 |
对表 2中的实验结果进行分析可以看出,01A级TH-1卫星影像附带的星历参数存在较大的系统误差,而且X方向的误差比Y方向和高程方向的要大。利用基于轨道外推的定位技术,可实现高精度的无控定位,定位精度X方向均值11.57 m,在地面2.5像元之内,最大值13.23 m,在3个像元之内;Y方向均值10.48 m,最大12.21 m,在地面2.5像元之内;Z方向均值10.34 m,最大值12.22。稀少控制定位在无控定位的基础上,加入1个控制点进行再次平差,定位精度相对于无控定位精度又得到了进一步提高,X方向精度均值9.93 m,在地面2个像元之内,最大值11.71 m,在2.5个像元之内;Y方向均值8.27 m,最大10.01 m,在地面2像元之内;Z方向均值7.59 m,最大值9.01。精度水平大约提高了0.5个像元。
3) TH-1图像864_146的有控定位。 在不利用标定参数和轨道外推技术的条件下,从6景影像中挑选控制点较多和分布较为均匀的864_146景影像(见图 5)进行基于地面控制的定位研究。实验方案包括两种:(1)以角元素为平差对象,检验不同数量控制点条件下的定位精度,并将其精度与无控定位和稀少控制定位精度进行比较;(2)以10个标定参数为平差对象,研究其精度与控制点数目的关系,并进行精度评定。

|
| 图 5 TH-1图像864_146及控制点分布 Fig. 5 TH-1 Image864_146 and GCP Distribution |
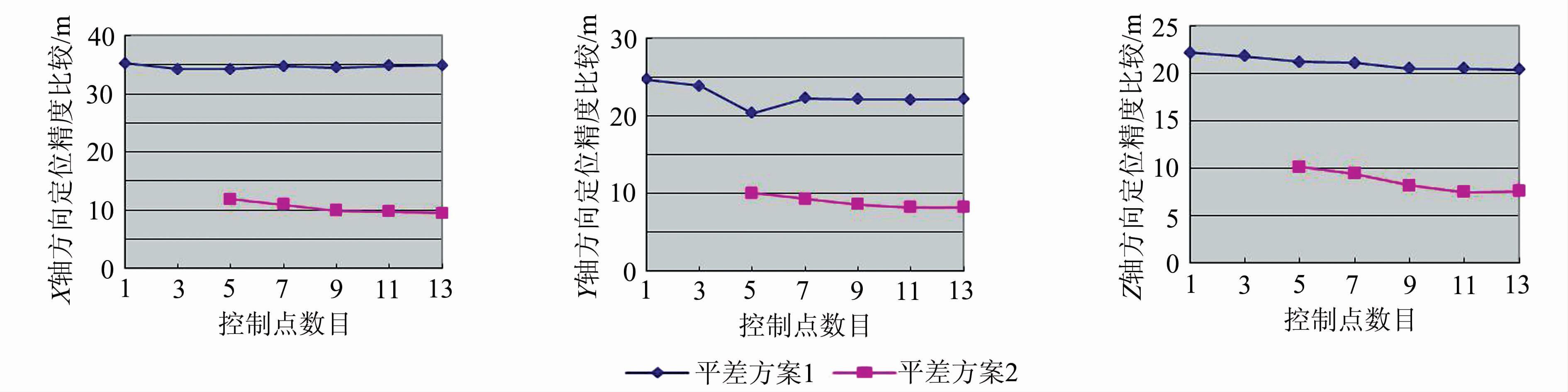
864_146上分布24个控制点,从中分别选取1、3、5、7、9、11、13个控制点(所采用的控制点分布见表 3第一列)进行第一种方案角元素的平差,剩余控制点作为检查点,定位结果见表 3第二列。对于第二种平差方案,经理论分析和实验证实在3个控制点时是无解的,其他情况下的平差结果见表 3第三列。将表 3中的实验结果绘图分析,得到图 6。
分析表 3和图 6可以得出以下结论:
1) 如果只考虑姿态观测数据转换得到的外方位角元素(φ,ω,κ)存在的误差,对角元素进行平差,精度虽然提高到X方向平均精度34.66 m、Y方向22.51 m、Z方向21.10 m,相对于直接定位精度得到了很大的提高,但是与无控定位、稀少控制和平差方案2的有控定位相比,精度仍然存在很大的差距。这说明TH-1卫星影像的定位误差不仅来源于姿态角观测值,还存在于焦距变化、交会角变化和主点变化等因素之中。
| GCP/CKP(控制点名) | 平差方案1 | 平差方案2 | |||||
| X | Y | Z | X | Y | Z | ||
| 1/23(3015) | 35.29 | 24.70 | 22.17 | - | - | - | |
| 3/21(3015、2040、1002) | 34.25 | 23.87 | 21.82 | - | - | - | |
| 5/19(3015、2040、1002、3072、2044) | 34.19 | 20.35 | 21.23 | 11.83 | 10.03 | 10.09 | |
| 7/17(3015、2040、1002、3072、2044、3070、1026) | 34.71 | 22.25 | 21.08 | 10.90 | 9.28 | 9.42 | |
| 9/15(3015、2040、1002、3072、2044、3070、1026、1014、2030) | 34.50 | 22.14 | 20.48 | 9.89 | 8.56 | 8.13 | |
| 11/13(3015、2040、1002、3072、2044、3070、1026、1014、2030、3019、2038) | 34.81 | 22.09 | 20.51 | 9.72 | 8.21 | 7.44 | |
| 13/11(3015、2040、1002、3072、2044、3070、1026、1014、2030、3019、2038、1003、1028) | 34.89 | 22.14 | 20.38 | 9.47 | 8.20 | 7.57 | |
| 平均值 | 34.66 | 22.51 | 21.10 | 10.36 | 8.86 | 8.53 | |
|
| 图 6 864_146影像两种不同平差方式下的精度比较示意图 Fig. 6 Accuracy Comparison of 864_146 Image by Two Different Approaches |
2) 随着控制点数目的增多,平差方案2有控定位的精度不断提高,当控制点增加到9个时,定位精度基本趋于稳定。
3) 将平差方案2的定位精度与表 2中864_146景影像的无控定位精度进行比较,5/19控制条件下,有控定位X和Y方向精度都略高于基于轨道外推的无控定位,Z方向精度明显高于无控定位精度。这证实了基于嵩山实验场的定标结果是非常可靠的,利用标定后的参数,基于轨道外推的定位技术可以有效提高定位精度,达到与充分地面控制条件相当的定位精度。
4) 将平差方案2的定位精度与表 2中864_146景影像的稀少控制定位精度进行比较,稀少控制定位精度与11/13控制条件下的定位精度接近,有控定位精度略高。这说明,在参数标定的基础上,如果具备少量的控制条件可以进一步提高定位精度,达到接近有控定位精度的水平。
4 总 结TH-1卫星三线阵CCD影像附带的定轨测姿数据带有系统误差,并且内方位元素等也存在一定的误差,利用定轨测姿参数进行直接空间前方交会存在非常明显的定位系统误差,必须采用平差技术对系统误差进行改正。 随着控制点数目的增多,有控定位的精度会进一步提高,但是当控制点数目增加到一定数量时,平差精度趋于稳定。 在具备可靠的标定参数的基础上,采用基于轨道外推的定位技术可以实现高精度的卫星影像定位。 稀少控制条件下,如果不具备标定后的参数,仅对外方位角元素进行平差解算,难以充分提高定位精度,还必须考虑存在于焦距和主点的误差,但是稀少控制条件不具备实现全部标定参数平差的能力。 稀少控制条件下,如果能够获得可靠的标定参数,则可以在基于轨道外推的定位技术的基础上,对角元素进行再次平差,进一步提高定位精度,得到接近有控定位的精度。
| [1] | Zhang Liang, Meng Chanyuan, Li Jun, et al. Precision Rectification Method for Island Satellite Image Based on Registration of Castline[J].Hydrographic Surveying and Charting,2011, 31(6):24-27(张靓,孟婵媛,李军,等.基于岸线配准的海岛(礁)遥感影像几何纠正方法[J].海洋测绘, 2011, 31(6):24-27) |
| [2] | Yang Tianke,Geng Xun,Wang Jianfeng,et al. Experiments About Large Scale Mapping by ADS40 Camera in Areas of Island and Reef[J]. Science of Surveying and Mapping, 2013,38(2):67-68(杨天克,耿讯,汪建峰,等.ADS40相机用于海岛(礁)大比例尺成图的试验[J].测绘科学,2013,38(2):67-68) |
| [3] | Lu Zhiping, Zhang Jianjun, Qiao Shubo.Geodesy Foundation[M]. Beijing:PLA Publishing House,2005(吕志平, 张建军, 乔书波. 大地测量学基础[M]. 北京:解放军出版社, 2005) |
| [4] | Wang Tao. Study on Theories and Methods of Linear CCD Sensor Geometric Calibration Based on Field[D]. Zhengzhou:Information Engineering University,2012(王涛.线阵CCD传感器实验场几何定标的理论与方法研究[D].郑州:信息工程大学, 2012) |
| [5] | Wang Jianrong, Yang Junfeng, Hu Xin, et al.2002.The Application of Three-dimensional Intersection for Calibrating the Spatial Camera[J].Journal of Institute of Surveying and Mapping, 2002,19(2):119-121(王建荣, 杨俊峰, 胡莘, 等.空间后方交会在航天相机检定中的应用[J]. 测绘学院学报, 19(2):119-121) |
| [6] | Yuan Xiuxiao,Yu Junpeng. Calibration of Constant Angular Error for High Resolution Remotely Sensed Imagery[J]. Acta Geodaetica et Cartographic Sinica,2008,37(1):36-41(袁修孝,余俊鹏.高分辨率卫星遥感影像的姿态角常差检校[J].测绘学报,2008,37(1):36-41) |
| [7] | Yuan Xiuxiao,Zhang Guo,Wu Chunhua. Extrapolative Location of High Resolution Remote Sensing Imageries[J].Geomatics and Information Science of Wuhan University, 2005,30(7):575-579(袁修孝,张过,吴春华. 缺少控制点的卫星遥感影像外推定位[J]. 武汉大学学报·信息科学版,2005,30(7):575-579) |
| [8] | Wang Renxiang, Hu Xin, Wang Jianrong. Photogrammetry of Mapping Satellite-1 Without Ground Control Points[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1):1-5(王任享,胡莘,王建荣.天绘一号无地面控制点摄影测量[J].测绘学报,2013,42(1):1-5) |
| [9] | Jiang Yanchuan. Analytical Photogrammetry[M].Beijing:PLA Publishing House,1991(江延川 |
| [10] | Yuan Xiuxiao.GPS Supported Aerial Triangulation Principle and Application[J].Beijing:Surveying and Mapping Press,2001(袁修孝.GPS辅助空中三角测量原理及应用[M].北京:测绘出版社,2001) |
 2016, Vol. 41
2016, Vol. 41


