文章信息
- 程春泉, 张继贤, 黄国满, 马晶
- CHENG Chunquan, ZHANG Jixian, HUANG Guoman, MA Jing
- 地心直角坐标系下的航摄光学影像严密定位模型
- Rigorous Positioning with Airborne Optical Images in ECEF
- 武汉大学学报·信息科学版, 2016, 41(5): 605-611
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 605-611
- http://dx.doi.org/10.13203/j.whugis20140148
-
文章历史
- 收稿日期: 2014-06-07

2. 地理空间信息工程国家测绘地理信息局重点实验室, 北京, 100830;
3. 长春工程学院, 吉林长春, 130021
2. Key Laboratory of Go-Informatics of State Bureau of Surveying and Mapping, Beijing 100830, China;
3. Changchun Institute of Technology, Changchun 130021, China
传统的航摄影像的严密定位大都是在地球切平面直角坐标系或地图投影坐标系中进行的[1, 2]。不同的坐标系各有特点,通常以满足应用需求并能简化处理作为物方坐标系的选择标准。由于影像数据来源越来越广,航天与航空遥感影像分辨率的差距也在逐渐消除,不同影像之间的联合处理会越来越紧密[3]。地理国情动态监测、非常规条件下的全球测图、应急情况下的测绘等项目相继开展,以及多源影像信息的提取与数据融合,对多源影像的联合平差处理提出了迫切需求。如在西部1∶5万测图工程中,文献[2]提出了难以布设控制点区域利用局部机载影像来控制星载影像的测图方法。多源影像的联合定位处理通常在一个统一的物方坐标系中进行,由于地心直角坐标系(Earth-centered Earth-fixed,ECEF)在航天光学与雷达遥感影像以及航空雷达影像中被广泛选为物方坐标系,加上该坐标系中严密模型不用考虑地球曲率以及不易受影像地理覆盖范围限制等特点,适宜作为多源数据联合处理的坐标系。因此,ECEF中航摄光学影像的严密定位模型研究,有利于促进多源遥感影像的联合处理。
1 地心直角坐标系姿态处理 1.1 欧拉角与四元数姿态处理的难点欧拉角中的数值都是角度,与人思考方位的方式相符,在应用上比较方便,是目前摄影测量中应用得最广泛的姿态表达方式。在切面直角坐标系和地图投影坐标系中,当航线接近南北方向时由旋转矩阵计算3个姿态欧拉角时偏航角解算面临奇异解问题。为了克服欧拉角参数的缺点,Rodrigues参数[4]、四元数[5]姿态参数在飞行器定向中得到应用。其中,四元数因构造矩阵不涉及三角运算、适合表达姿态旋转,且克服了姿态90°附近根据矩阵反算欧拉角存在奇异等不足,在遥感影像的对地目标定位中得到重视,也取得了重要进展,如龚辉等利用四元数实现了航空航天光学遥感影像的对地定位[6]。由于定位定姿系统(position and orientation system,POS)已成为航空航天摄影测量的基本工具,POS辅助下的遥感影像区域网联合平差,是当前稀少或无地面控制点条件下影像严密定位的基本方法[1, 7]。而四元数的4个参数除了不独立等不足外,在姿态参与多源观测数据的联合平差处理中,也还存在一些问题有待研究解决。
设ω为刚体绕瞬时轴旋转的角速度所对应的四元数,则四元数q的微分方程为[8]:

若惯性测量单元(inertial measurement unit,IMU)测量欧拉角(Ψ,Θ,Φ)分别为绕Z轴、Y轴、X轴的旋转角度,相应的四元数q(q0,q1,q2,q3)计算式为:
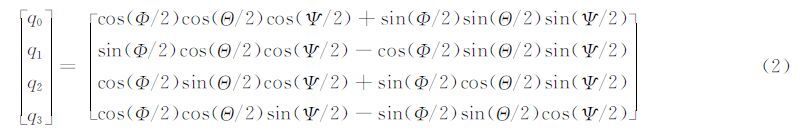
理论上四元数更适合从姿态动力学的角度来研究姿态的变化,但载机飞行时的受力异常复杂,姿态呈现不规则高频变化,几何定位中直接根据姿态动力学理论来确定载机姿态是很困难的。虽然航空摄影时姿态角是不规则地高频变化的,用欧拉角表达的IMU测量姿态误差的变化仍呈现规律性和系统性,实际应用中通常利用时间的低阶多项式即可高精度拟合其误差[1, 9],处理简单,且欧拉角姿态误差与测量值大小无关。根据式(1)或式(2)导出的误差传播公式可以看出,四元数4个参数的误差不仅与初值误差和时间相关,还与姿态初值大小相关,航空IMU高频变化姿态系统误差四元数表达是一个待深入研究的问题。同时,精度是多源数据联合处理的一项重要的信息,IMU姿态测量精度通常以欧拉角的形式给出。姿态测量给定欧拉角精度时,载机不同方向飞行而具有不同姿态初值时四元数的4个参数值对应的“精度”是不固定的,四元数“精度”和“权”的表达是姿态参与多源数据联合平差需解决的另一个难点。克服或避开欧拉角和四元数在应用上的这些难点,可以方便它们在摄影测量中的应用。
1.2 初始四元数与偏置欧拉角结合的姿态精化传统的姿态修正是直接在摄影测量坐标系(物方坐标系)中的姿态初值(ω0,φ0,κ0)上加上修正参数(Δω,Δφ,Δκ)来实现的。本文根据ECEF下航摄遥感影像定位的需要,以四元数记录ECEF中传感器原始姿态,通过欧拉偏置角实现姿态定向精度的提高,进而实现光学航摄影像的严密几何处理。由于原始姿态矩阵RbE(ω0,φ0,κ0)和精化后的姿态矩阵R′bE(ω0+Δω,φ0+Δφ,κ0+Δκ)之间必有一组补偿偏置角参数 (Δω′,Δφ′,Δκ′),使得精化后的姿态精化矩阵R′bE满足:
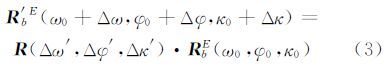
故对姿态初值(ω0,φ0,κ0)增量未知数(Δω,Δφ,Δκ)的求解可以转变为对偏置角未知数(Δω′,Δφ′,Δκ′)的求解,使得精化后的姿态旋转矩阵不变。
当ECEF作为姿态参考基准时,本体坐标系到ECEF的转换矩阵RbE计算量较大,且在空中三角测量迭代过程中存在重复的计算,降低了计算效率。当采用上述偏置角进行姿态修正时,RbE仅与ECEF中的姿态初值有关,可以将IMU测量姿态初值归算到地心坐标系后直接用四元数来记录,平差计算时可方便利用四元数构造初始姿态矩阵,进而提高平差处理的速度。
令IMU本体坐标系到ECEF转换矩阵RbE(ω0,φ0,κ0)对应的姿态四元数为q(q0,q1,q2,q3),其对应的旋转矩阵记为RbE(q),则精化后的姿态矩阵R′bE可表达为:
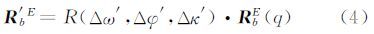
经过上述处理,欧拉偏置角 (Δω′,Δφ′,Δκ′)的初值均为0,且其精度可直接继承IMU姿态测量值的精度。同时,补偿偏置角通常接近0,不会出现偏置角求解奇异、多值现象。
文献[10]利用偏置矩阵提高了光学卫星影像的自主定位精度,本文利用偏置角来精化姿态并实现影像的严密空中三角测量。偏置角 (Δω′,Δφ′,Δκ′) 的求解与传统的姿态增量未知数(Δω,Δφ,Δκ)的求解一样,将其代入姿态旋转矩阵中并通过对共线方程线性化得到的像点误差方程来求解。
2 基于补偿偏置角的光学航摄影像严密定位 2.1 姿态和位置的归算ECEF下进行摄影测量,需要利用IMU测量值计算ECEF中的姿态角或姿态转换矩阵。POS的姿态参考系统为导航坐标系,又称为北东地坐标系,姿态为Z-Y-X转角系统下的姿态角(Ψ,Θ,Φ)。
POS的欧拉角姿态为0时,IMU本体坐标系的三轴与导航坐标系的三轴平行,但Y轴和Z轴的方向相反。因此,IMU本体坐标系到导航坐标系的转换矩阵Rbn为:
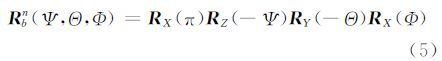
设相应姿态测量时刻传感器的地理位置为(Ln,Bn),可由GPS测量得到。则导航坐标系到ECEF的转换矩阵为:
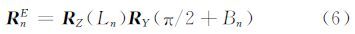
因此,IMU本体坐标系到ECEF的姿态旋转矩阵为RbE=RnERbn。设RbE对应的四元数姿态为q(q0,q1,q2,q3),依次绕X-Y-Z轴旋转对应的欧拉角姿态为ω、φ、κ,则有:
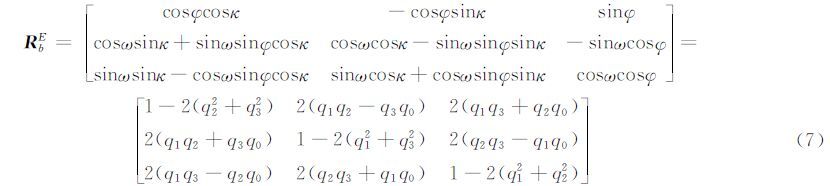
设RbE矩阵元素为aij(i,j=0,1,2),根据式(7)可计算欧拉角ω、φ、 κ:
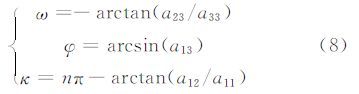
同样,根据四元数的性质和式(7),可按下列四组公式之一计算四元数:

在ECEF中,3个欧拉姿态角的取值范围均扩大到-180°~180°,且受航摄地理位置、飞行方向、航摄姿态大小的影响,根据式(8)求解欧拉角姿态时更容易遇到奇异和需对多解进行判定的问题;根据式(9)求得的四元数参数中某个值也可能为0或接近0,四元数也可能存在病态解,但可通过对4组四元数第一个参数解算值的判断,选取一组稳定的解。同时,从式(7)可以看出,利用四元数构造姿态矩阵不涉及三角函数计算,计算机运算速度比欧拉角姿态更快。因此,选用四元数记录ECEF中初始姿态在计算稳定性和后继平差迭代速度上,有一定的优势。
传感器与GPS接收机、IMU共同安置在同一个摄影平台中,摄影期间,可以认为它们三者之间的几何关系是固定的,可以通过6个参数来确定传感器外定向参数与GPS和IMU测量值间的关系,即IMU本体坐标系中传感器投影中心相对于GPS天线中心的安装偏心距eXs、eYs、eZs,传感器坐标系相对于IMU本体坐标系的安装偏置角eω、eφ、eκ。在ECEF中,GPS天线中心位置(XGPS,YGPS,ZGPS)与传感器镜头中心(XS,YS,ZS)有如下关系:
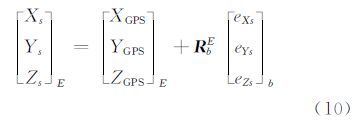
传感器坐标系到ECEF的转换矩阵可表示为:
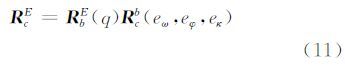
当考虑补偿偏置角(Δω′,Δφ′,Δκ′)和传感器安装偏置角误差(Δeω,Δeφ,Δeκ)时,姿态精化后的矩阵R′cE为:
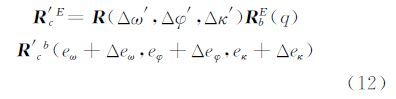
在不需要考虑传感器安装偏置角误差的情况下,安装偏置角可一并归算到四元数中,以简化模型。
2.2 地心直角坐标系下光学航摄遥感的严密定位
设RcE或R′cE的矩阵元素为mij(i,j=0,1,2),则有ECEF中航摄影像的共线方程:
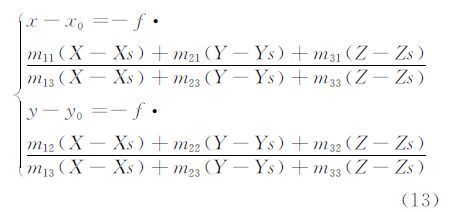
式中,(x,y)为像点坐标;(x0,y0)为像主点坐标;(X,Y,Z)为地面点坐标;(Xs,Ys,Zs)为ECEF中传感器投影中心的坐标。
由于偏置姿态仍采用欧拉角参数,偏置姿态和GPS系统误差仍采用低阶多项式来表达,有:
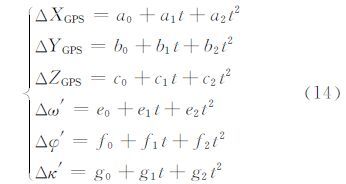
式中,ai、bi、ci、di、ei、fi、gi (i=0,1,2)为位置和姿态系统误差多项式系数。
由于欧拉偏置补偿角有初值和精度信息,仍可以方便地与其他观测值一起进行联合平差。以地面点坐标增量、GPS位置、补偿偏置角及其系统误差多项式系数、传感器安装偏置增量参数、像方坐标系统误差参数作为未知数,将式(14)分别作为观测值误差方程和严格方程时,构建两种形式的空中三角测量误差方程组:
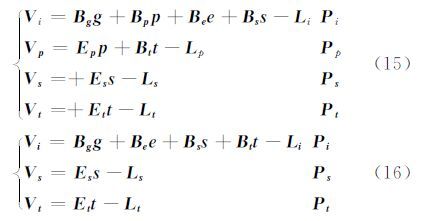
式中,Vi、Vp、Vs、Vt分别为根据式(13)构建的像点坐标、根据式(14)构建的影像摄影时刻POS外方位元素、像方坐标系统误差参数以及POS系统误差多项式系数虚拟观测值的改正数向量;g、p、s、e、t分别代表加密点坐标增量未知数向量[ΔX ΔY ΔZ]、摄影时刻定向未知数向量[ΔXGPS ΔYGPS ΔZGPS Δω′ Δφ′ Δκ′]、像方坐标系统误差参数未知数向量、传感器安装偏置距与偏置角(含IMU视轴)增量未知数向量[ΔeXs ΔeYs ΔeZs Δeω Δeφ Δeκ]以及POS系统误差低阶多项式系数未知数向量[ai bi ci ei fi gi];Bg、Bp、Be、Bs、Bt、Es、Ep、Eg、Ee为相应未知数系数的设计矩阵;Li、Lp、Ls、Lt为相应观测方程的常数项向量;Pi、Pp、Ps、Pt为相应观测值的权矩阵。
式(15)可用于框幅式/面阵影像的空中三角测量处理,以及基于定向片模型的线阵影像处理,其中的Vi由式(10)、式(12)代入式(13)后线性化得到,Vp根据式(14)构建。式(16)用于线阵影像基于一般多项式模型的空中三角测量处理,其中的Vi由式(10)、式(12)和式(14)代入式(13)后线性化得到。线阵影像定向片模型的定向参数补偿值为该时刻邻近的两个定向片时刻的增量Δpk、Δpk+1内插得到,即Δpj=t·Δpk+(1-t)Δpk+1(t为定向片间的归一化时间) ,故Vi涉及到摄影时刻邻近的两个定向片参数,线阵影像一般多项式模型的修正值由式(14)完全确定,框幅式影像的修正值与式(14)间存在最小二乘意义上的相等。摄影时刻定向参数初值由该时刻邻近的GPS测量值和四元数插值而成,初值与补偿值一起,获得精化后的定向参数。与文献[11]一样,本文处理方法保存了POS测量值的高频变化信息。
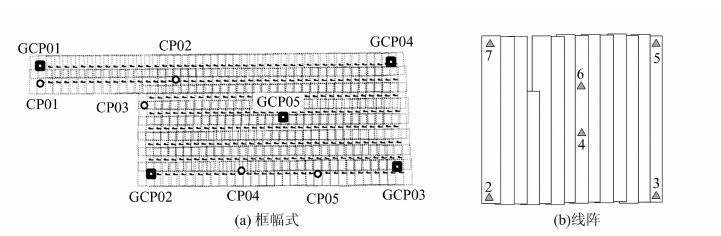
3 实 验 3.1 实验数据本文采用光学框幅式影像与线阵影像对模型的正确性进行了验证。框幅式影像实验区选在西部地区,测区地面高程为170~750 m,摄影航高为2 400 m。航摄仪焦距较短,为88.785 mm,航摄仪未经过检校。影像为航摄负片经扫描而成的数字化影像,扫描孔径为23 μm,影像地面分辨率为0.6 m,影像大小为11 200×11 200像素,航摄目的为资源调查和变化监测。有8条航带共282幅影像,航带和影像分布如图 1所示。在实验区实地测量了10个地面控制点,编号为GCP01~GCP05的5个点设为定向点,分布在影像四角和中心位置; CP01~CP05的5个点作为检查点,分布在控制弱区,如图 1(a)所示。线阵影像采用ADS40影像,航摄仪焦距为62.7 mm,像元大小为6.5 μm,影像地面分辨率为0.3 m,航高为4 800 m,共有14个条带,测区南北长约44 km,东西宽约30 km,测区平均高程为2 100 m,高差约350 m,为丘陵和山区地形。测区内四角和中间位置共测量了6个地面控制点,分布如图 1(b)所示。经影像匹配获得了两测区重叠影像内足量的像片连接点。
|
| 图 1 框幅式和线阵影像及地面控制点分布 Fig. 1 Distribution of Ground Points for Frame Images and Three Line Sensor Images |
本文中,像方坐标系统误差补偿采用Brown模型[12],线阵影像外方位元素拟合采用一般多项式模型,每个条带影像的前、中、后视影像采用一组独立的精化参数,定向片模型则按每条航线设置一组参数,定向片间隔为8 s。由于物方坐标系为地心直角坐标系,计算得到的地面点坐标Z值不代表高程,本文将地面点坐标经过坐标系和投影转换后,得到投影坐标系中的值,用于加密精度评价。
1) 框幅式影像的定位。 以定向点和影像间的连接点为基础,解算式(13)列立的误差方程组,获得每一张影像的定向参数。以精化后的定向参数和影像坐标按前方交会计算相应的地面点坐标。将计算值与已知值进行比较,得到各点位置误差如表 1所示。同时,也在切平面直角坐标系中进行了同等条件的定位实验,结果见表 1。
| 点号 | 地心直角坐标系下 | 地球切平面直角系下 | |||
| 平面 | 高程 | 平面 | 高程 | ||
|
定 向 点 | GCP01 | 0.302 | 0.328 | 0.301 | 0.325 |
| GCP02 | 0.536 | 0.376 | 0.533 | 0.376 | |
| GCP03 | 0.658 | -0.428 | 0.654 | -0.430 | |
| GCP04 | 0.600 | 0.316 | 0.603 | 0.314 | |
| GCP05 | 0.510 | -0.463 | 0.508 | -0.462 | |
| RMSE | 0.535 | 0.386 | 0.533 | 0.386 | |
|
检 查 点 | CP01 | 0.534 | 0.483 | 0.532 | 0.485 |
| CP02 | 0.891 | 0.826 | 0.889 | 0.827 | |
| CP03 | 0.963 | -0.770 | 0.960 | -0.769 | |
| CP04 | 0.801 | -0.862 | 0.799 | -0.863 | |
| CP05 | 1.008 | -0.984 | 1.009 | -0.987 | |
| RMSE | 0.856 | 0.803 | 0.855 | 0.804 | |
2) 机载三线阵影像的定位实验。 实验分别进行无控制点条件下的自由网平差,1个定向点 (依次选取4、6作为定向点,其余作检查点)、4个定向点(四角点)、5个定向点(依次选取1个点作检查点,其余作定向点)条件下的区域网平差,得到一般多项式和定向片模型精度见表 2。
| 模型 | 一般多项式模型 | 定向片模型 | |||||||
| 定向点数 | 0 | 1 | 4 | 5 | 0 | 1 | 4 | 5 | |
|
定 向 点 | 平面精度 | - | 0.05 | 0.21 | 0.20 | - | 0.03 | 0.17 | 0.18 |
| 高程精度 | - | 0.08 | 0.17 | 0.19 | - | 0.05 | 0.16 | 0.17 | |
| 平面最大误差 | - | 0.05 | 0.29 | 0.32 | - | 0.03 | 0.27 | 0.29 | |
| 高程最大误差 | - | 0.08 | 0.21 | 0.23 | - | 0.05 | 0.19 | 0.19 | |
|
检 查 点 | 平面精度 | 0.64 | 0.56 | 0.34 | 0.35 | 0.69 | 0.59 | 0.32 | 0.33 |
| 高程精度 | 0.59 | 0.45 | 0.31 | 0.33 | 0.56 | 0.44 | 0.29 | 0.30 | |
| 平面最大误差 | 1.02 | 0.83 | 0.39 | 0.44 | 1.06 | 0.88 | 0.38 | 0.42 | |
| 高程最大误差 | 0.91 | 0.80 | 0.35 | 0.37 | 0.94 | 0.81 | 0.32 | 0.35 | |
对于不同类型光学航摄影像在不同条件下的定位所具有的性质和特点已有较多的文献进行了论述[1, 5, 7],本节重点对本文模型本身进行分析。
1) 本文提出的ECEF下航摄光学影像姿态精化模型可以用于空中三角测量,解决了ECEF中姿态处理难点。相应的光束法区域网平差模型能够吸收传统航摄光学影像严密定位成熟的处理方法,可用于航摄框幅式和线阵传感器影像稀少或无控制点条件下的严密定位,且不受地球曲率的限制影响,加密精度与切平面直角坐标系下的处理精度一致。
2) 与当前基于四元数的光学影像加密方法相比,避开了四元数在多源数据联合平差和高频变化POS姿态系统误差表达中的难点,POS姿态初值与精度信息得到利用,能够方便地通过POS与影像数据联合平差的方式实现稀少或无地面控制点条件下航摄光学影像的严密定位。
3) 四元数初始姿态与偏置角补偿姿态结合的处理方法,避开了ECEF中欧拉角姿态-180°~180°范围内的求解可能出现的奇异问题,初始姿态或精化后姿态计算不受测区地理位置以及载机飞行方向的影响,有利于姿态处理的稳定性。
4) 从模型的构建过程看,如果将本文四元数姿态初值替换为传感器坐标系到切平面直角坐标系中的姿态,理论上模型仍可方便应用于切平面直角坐标系航摄光学影像的空中三角测量;如果将四元数初值替换为ECEF中星载传感器的姿态,也可方便地应用于航天光学遥感影像的定位。
本文在ECEF下建立的POS辅助光学航摄影像光束法区域网平差模型是正确的,与ECEF中航天光学、雷达影像以及航空雷达影像几何模型相结合,理论上可以方便地在统一的地心直角坐标系中实现包括航空光学影像在内的多源数据的联合平差,可望实现对日益丰富的多源遥感影像进行一体化几何处理,从而提升数据的利用率,拓展几何模型对多源遥感影像数据的处理能力。
| [1] | Yuan Xiuxiao. POS-supported Bundle Block Adjustment[J]. Acta Geodaetica et Cartographica sinica,2008,37(3):342-348(袁修孝. POS辅助光束法区域网平差[J],测绘学报,2008.37(3):342-348) |
| [2] | Zhang Jixian, Yan Qin, Zhang Li, et al. Principle and Methodology of Western China Topographic Mapping[M]. Beijing:Surveying and Mapping Press,2013(张继贤,燕琴,张力,等.西部地形困难区域测图的原理和方法[M].测绘出版社,2013) |
| [3] | Jordi I, Alain G. On the Possibility of Automatic Multisensor Image Registration[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42(10):2104-2120 |
| [4] | Er Schaub H, Junkins J L. Steregraphic Orientation Parameters for Attitude Dynamics:A Generalization of the Rodrigues Parameters[J].The Journal of the Astronautical Sciences, 1996, 44(1):1-19 |
| [5] | Liu Jun, Wang Donghong, Zhang Yongsheng, et al. Bundle Adjustment of Airborne Three Line Array Imagery Based on Unit Quaternion[J].Acta Geodaetica et Cartographica Sinica,2008,37(4):451-457(刘军,王冬红,张永生,等. 基于单位四元数的机载三线阵影像光束法平差[J].测绘学报, 2008, 37(4):451-457) |
| [6] | Gong Hui,Jiang Ting, Jiang Gangwu,et al.Bundle Block Adjustment of Aerial Imagery Based on Unit Dual Quaternion[J]. Geomatics and Information Science of Wuhan University, 2012,37(2):154-159(龚辉,姜挺,江刚武,等.利用单位对偶四元数进行航空影像区域网平差解算[J]. 武汉大学学报·信息科学版,2012,37(2):154-159) |
| [7] | Yuan Xiuxiao. Principle and Application of GPS-supported Aerotriangulatiion[M]. Beijing:Surveying and Mapping Press,2001(袁修孝.GPS辅助空中三角测量[M]. 北京:测绘出版社,2001) |
| [8] | Zhang Renwei. Satellite Orbit-Attitude Dynamics and Controlling[M].Beijing:Beijing University of Aeronautics and Astronautics Press,1998(章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,1998) |
| [9] | Ackerm A F. Practical Experience with GPS-supported Aerial Triangulation[J]. Photogrammetric Record,1994,16(84):861-874 |
| [10] | Zhang Guo, Yuan Xiuxiao, Li Deren. Redressing System Error in Satellite Image Based on Bias Matrix[J]. Journal of Liaoning Technical University, 2007,26(4):517-519(张过,袁修孝,李德仁.基于偏置矩阵的卫星遥感影像系统误差补偿[J].辽宁工程技术大学学报,2007,26(4):517-519) |
| [11] | Hinsken L, Miller S, Tempelmann U, et al. Triangulation of the LH Systems' ADS40 Using ORIMA GPS/IMU[C]. ISPRS Commission Ⅲ, Photogrammetric Computer Vision,Graz,2002 |
| [12] | Brown D C. The Bundle Adjustment:Progress and Prospects[C]. The 8th Congress of the International Society for Photogrammetry, Helsinki,1976 |
 2016, Vol. 41
2016, Vol. 41


