文章信息
- 郑顺义, 桂力, 王晓南
- ZHENG Shunyi, GUI Li, WANG Xiaonan
- 二维线划图中建筑物檐口高自动提取方法
- A Method of Automatic Eaves Height Determination for Buildings in 2D Digital Line Graph
- 武汉大学学报·信息科学版, 2016, 41(5): 584-589,611
- Geomatics and Information Science of Wuhan University, 2016, 41(5): 584-589,611
- http://dx.doi.org/10.13203/j.whugis20140126
-
文章历史
- 收稿日期: 2015-01-12

2. 地球空间信息技术协同创新中心, 湖北武汉, 430079
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China
当前我国基础地理信息部门存在大量的二维线划图,它们的主要特点是有精确的平面位置,高程信息以注记或等高线的方式描述,不是由三维几何要素组成的真三维地图。这些二维线划图的出现有以下原因:(1)线划图是从纸质地图经过数字化得到的,原始地图本身就是二维的[1, 2];(2)线划图是用传统工程测量仪器测得的[3],比如全站仪等,这些仪器对应的测图软件或工具本身是二维的;(3)通过数字摄影测量工作站测得的地图本身是三维的,但在导入到后续的出版编辑软件时丢掉了高程信息,只保留了平面信息,原因是早期的这些软件不具备处理三维线划图的能力[1]。以前,二维线划图对于平面定位、目标寻找和简单的选址规划能满足要求,但随着城市建设的深入和技术的进步,人们需要更多的三维空间智能分析、三维设计规划等功能,如对建筑物顶部的管道、电气、通风等附属设施进行智能管理需要提供精确的檐口高度,而二维线划图已无法满足这些需求[2, 4, 5]。目前三维线划图的自动化提取还存在很多困难,基本是人工绘制,重新采集三维线划图需要很多的人力物力。因此,在这种情况下,研究一种给二维线划图上的建筑物自动赋值高程从而变成三维线划图的技术方法,就显得非常有意义和有必要。
檐口指大屋面最外边缘处的屋檐位置,檐口高即指地面到檐口位置的高度,一般意义上也作为建筑物高。目前有多种获取檐口高的方法,较常用的测量方式有摄影测量方法[1]和工程仪器直接测量法[2],这两种方法测量精度高,但需大量人力劳动。基于单张影像也可获取檐口高,如文献[6, 7, 8, 9]利用阴影进行高度提取,文献[10, 11, 12]利用灭点获取建筑物高,这些方法对数据依赖性强,其结果误差偏大,在实际生产应用中有较多的局限性。本文提出了一种给二维线划图中建筑物自动赋值高程的方法。该方法利用现有二维线划图,结合对应影像的内外参数,首先通过一种极大值边缘信息量计算方法获取建筑物初始高度,然后经过广义点摄影测量迭代求解,获取建筑物的精确檐口高。
1 基于极大值边缘信息量的高程初值提取建筑物的檐口位置在影像上表现为多种连续线状特征[13],如墙沿、附属物边沿等具有明显线性边缘的地物,而其他位置则没有表现出大量的连续线性边缘特征。根据这一特点,可以通过搜索最大边缘信息量来定位檐口高度。参照共线方程[1],对构成二维线划图中的建筑物多段线的每个点(Xi,Yi)进行投影,获取点在对应影像上的坐标(xNi,yNi)。多段线在多视影像上投影的基本数学公式为:
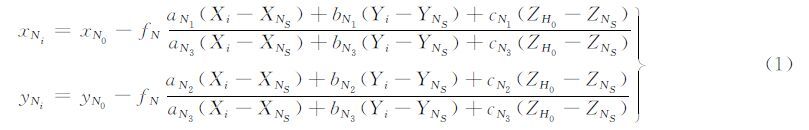
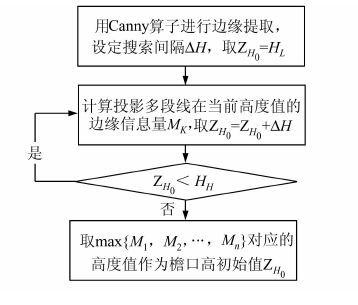
式中,下标N表示投影到第N张影像上N≥1;xN0、yN0、fN为影像的内方位元素; (XNS,YNS,ZNS)为摄站点的物方空间坐标;aNK、bNK、cNK(K=1,2,3)为影像的3个外方位角元素组成的9个方向余弦。设定整个区域内建筑物檐口高最小值HL与最大值HH,对某个二维建筑物多段线分别用最小与最大高度值进行投影,如果多段线中有超过一半的端点落在该影像上,则认为该影像可以参与计算,记可参与计算影像总数为In。设定高程搜索间隔ΔH,对所有参与计算的影像利用Canny算子分别进行边缘提取,提取后的二值影像作为边缘影像,根据如图 1所示的流程进行初始值计算。通过该方法利用一张或者多张影像可实现线划图与建筑物在檐口位置的整体套合。
|
| 图 1 檐口高初始计算流程 Fig. 1 Flowchart of Initial Eaves Height Determination |
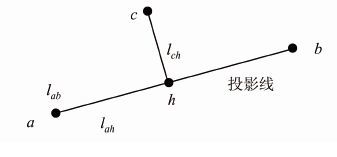
图 1中边缘信息量的计算方法为:对每条投影线段,以ΔL为间隔对线段进行离散化,记LN为多段线的离散长度。对于每个离散点,在边缘影像中搜寻该点处垂直于线段方向上一定距离内的最近边缘点(见图 2),线段ab上的某一点h在搜索方向上的像素坐标xc,yc可计算公式为:
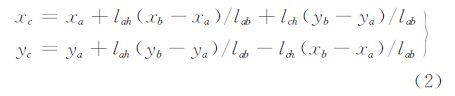
|
| 图 2 边缘信息量计算示意图 Fig. 2 Diagram of Edge Information Calculation |
式中,(xa,ya)、(xb,yb)分别为点a、b的像素坐标;lah、lab、lch分别为线段ah、ab、ch的长度。
如果搜索到最近边缘点,记PN=PN+1。其中,PN为多段线在第N张影像上搜索到的边缘点个数。计算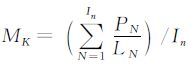 作为本次的边缘信息量值,其中
作为本次的边缘信息量值,其中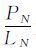 为投影在第N张影像上多段线能够搜索到边缘信息的比例,该值越大表明在当前位置沿各线段方向的边缘信息越丰富,对所有投影影像上的比例求和后取平均即得到整体的边缘信息量。MK作为边缘信息量指标能够直观地衡量檐口边缘信息,使用归一化的表达方式使得不同目标间的信息量具有可比性,同时对多张影像上的信息进行综合,可消除少量非边缘信息的干扰。在该指标最大值处能够获得建筑物最多的檐口信息,为下一步精确计算提供初始值,其大小随高程的变化趋势可参看实验部分初始值计算结果。
为投影在第N张影像上多段线能够搜索到边缘信息的比例,该值越大表明在当前位置沿各线段方向的边缘信息越丰富,对所有投影影像上的比例求和后取平均即得到整体的边缘信息量。MK作为边缘信息量指标能够直观地衡量檐口边缘信息,使用归一化的表达方式使得不同目标间的信息量具有可比性,同时对多张影像上的信息进行综合,可消除少量非边缘信息的干扰。在该指标最大值处能够获得建筑物最多的檐口信息,为下一步精确计算提供初始值,其大小随高程的变化趋势可参看实验部分初始值计算结果。
通过上文计算过程可得到初始檐口高度,由于其计算结果受搜索的步距和宽度影响,需进一步精化处理。另外,二维线划图是以建筑物所在地面作为基准,少量线段与檐口位置会有一定偏移,也需对线段在檐口处的位置进行微调。考虑檐口位置处大量的线状特征,本文基于广义点摄影测量理论对檐口高进行精化计算。广义点摄影测量把传统摄影测量中物理意义上的点看作数学意义上的点统一纳入到传统的摄影测量共线方程中进行平差,它不需要影像点与空间点的严格对应关系,而是在平差迭代过程中逐步实现像点与空间点的一一对应。广义点摄影测量的基本数学公式为[13]:
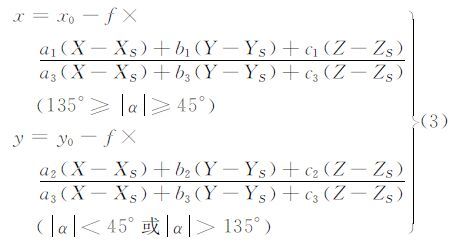
设投影在影像上的直线l在Z=ZH的空间平面上对应的空间直线L的方程[13]为:
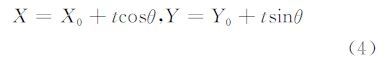
将相关参数代入式(4),再代入广义点摄影测量式(3)得:
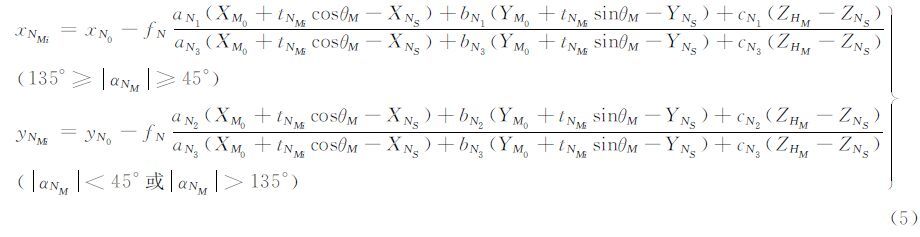
式中,下标M表示建筑物多段线中第M条线段;N表示参与处理的第N张影像;xNMi,yNMi为边缘像点坐标;tNMi为直线参数;XM0、YM0、θM、ZHM为待求解的空间直线参数。将式(5)线性化,即可得到广义点摄影测量的数学平差模型:
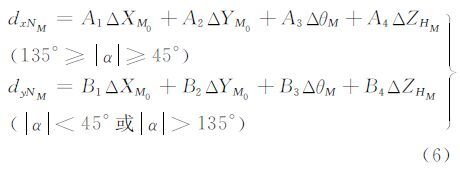
式中,A1、A2、A3、A4和B1、B2、B3、B4为改正数系数;dxNM 、dyNM为常数项。
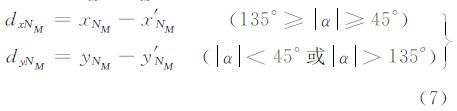
式中,(xNM,yNM)为直线段投影到影像上的轮廓点坐标;(x′NM,y′NM)为影像上的真实轮廓点坐标,图 3所示为精确值求解示意图。
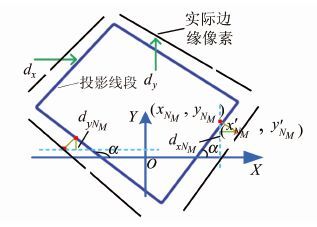
|
| 图 3 檐口高精确提取示意图 Fig. 3 Diagram of Precise Eaves Height Extraction |
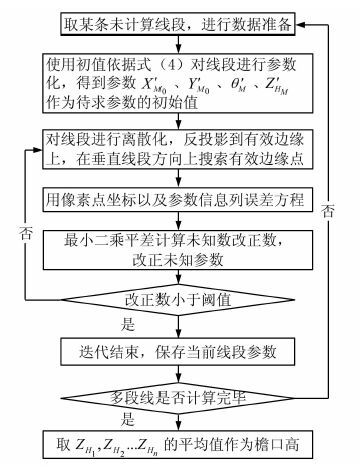
精确值计算主要包括有效边缘数据准备和广义点迭代两个过程,数据准备过程中对不稳定边缘进行剔除。不稳定边缘形成的主要原因有:① 摄影角度因素造成檐口轮廓不明显;② 地物本身无明显边缘;③ 边缘遮挡、阴影干扰等。数据准备步骤为:① 去掉多段线中短小的拐角线段;② 取某条未计算线段,保留一定宽度内边缘,用Hough变换对边缘点做直线提取;③ 搜索提取的线段中边缘点数最多的线段,若其像点占投影线段比例大于一定阈值则为有效边缘,投影所有影像进行计算并统计有效边缘总数;④ 若有效边缘总数不小于2,则认为可参与迭代计算,否则舍去该线段。图 4为精确值具体计算流程。
|
| 图 4 檐口高精确计算流程 Fig. 4 Flowchart of Precise Eaves Height Determination |
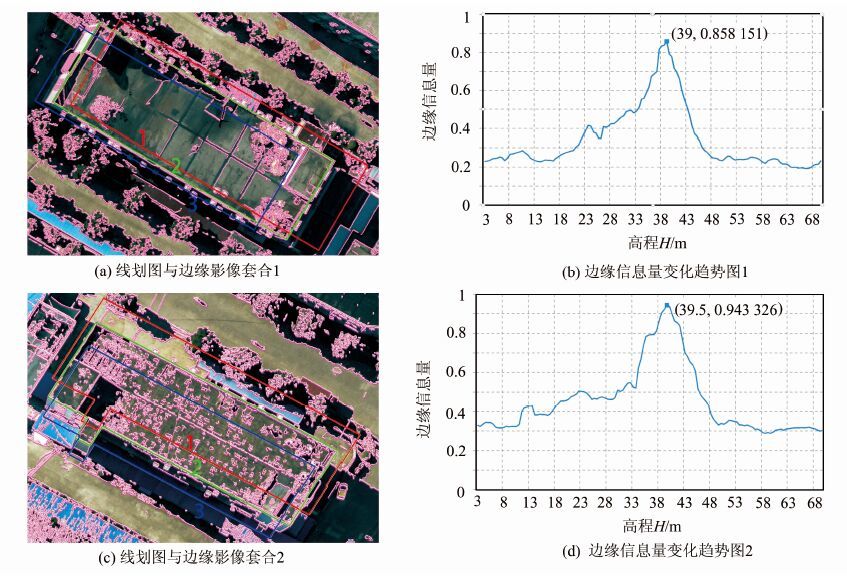
本文实验影像为浙江嵊州地区无人机航飞数据,影像大小为6 732×8 984像素,影像内外参数已知,二维线划图为该地区已有旧数据。首先对CAD格式的二维线划图数据进行解析,通过建筑物图层索引号提取其中的建筑物多段线。根据实验区域建筑物高度情况,设置HL=3 m,HH=70 m,搜索间距ΔH=0.5 m,边缘点搜索距离为8像素。利用§1节方法进行处理,可得到初始高程提取结果。如图 5(a)、5(c)所示为通过极大值边缘信息量计算方法得到的建筑物二维多段线与对应边缘影像、原始影像的套合,其中图 5(a)、5(c)中所标1、2、3分别为设定最大高、极大值边缘高、设定最小高三个位置,从图 5(a)、5(c)中可以看出在极大值边缘位置处线划图与边缘影像在檐口位置套合较好。图 5(b)、5(d)为搜索过程中边缘信息量随着檐口高变化的情况,从图 5(b)、5(d)中可以看出边缘信息量在高度到达檐口位置之前呈现上升趋势,而在超过檐口位置后则呈现下降趋势,在檐口位置具有最大值。
|
| 图 5 檐口高初始值求解结果 Fig. 5 Results of Initial Eaves Height |
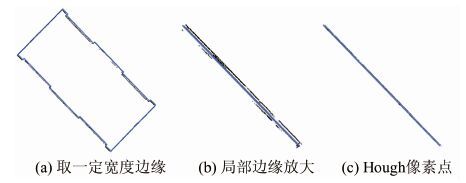
图 6为精确计算的数据准备过程,其中图 6(a)为取投影线段一定宽度内像素点作为Hough变换提取直线的候选点,图 6(b)为局部放大影像,图 6(c)为Hough变换后保留下来的像素与投影线叠加。图 7为精确檐口高赋予线划图后投影到影像上的情况,从叠加投影效果可以看出,投影线与建筑物实际檐口位置吻合效果较好,正确恢复了檐口高度信息。为进一步验证结果的可靠性,本文使用计算的精确檐口高,结合二维线划图和影像数据,对建筑物进行三维建模并映射纹理(如图 8),从三维模型上可以看出纹理与几何模型一致性较好,在檐口位置没有出现纹理偏离现象。
|
| 图 6 数据准备过程 Fig. 6 Data Preparation Procedure |

|
| 图 7 檐口高精确值求解结果 Fig. 7 Results of Precise Eaves Height Determination |

|
| 图 8 基于建筑物檐口高的三维重建结果 Fig. 8 Reconstructed Results of Buildings Based on Eaves Height |
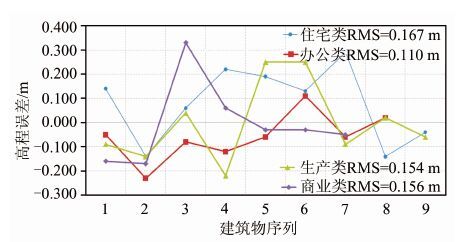
为定量评价本文方法的精度,选取了33栋不同类型的建筑物进行计算,获取每栋建筑物檐口高,以人工立体测图方式获取并经过外业测量检验的檐口高度值作为真值进行对比。同时为检验本文算法对不同类型建筑物的适应性,依照建筑物功能对其进行了类型划分并给出大致空间分布(如图 9所示)。图 10为4种类型建筑物解算结果的误差分布图,从图中可看出建筑物的整体中误差不超过0.17,能满足较高的精度要求。4种类型建筑物的高程误差总体趋势较为一致,其中办公类精度稍优于平均水平,与该类房屋周边干扰信息较少有关,结果表明本文算法对不同类型的建筑物具有较好的适应性。

|
| 图 9 不同类型建筑物空间分布 Fig. 9 Spatial Distribution of Different Types of Buildings |
|
| 图 10 檐口高误差分布图 Fig. 10 Chart of Eaves Height Error Distribution |
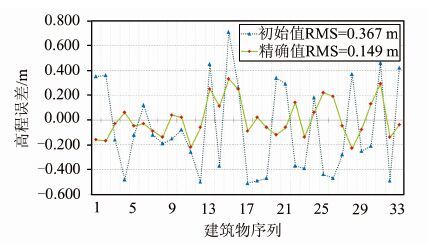
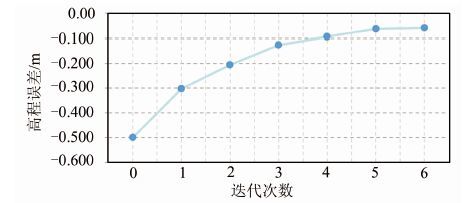
为验证精化过程的有效性,对上述建筑物求取其初始值误差与精确值误差进行对比,对比结果如图 11所示,其初始值中误差(RMS)为0.367 m,精确值中误差为0.149 m,从图 11中可以看出精化计算提高了檐口高度求解的精度和稳健性。为说明本文算法迭代的收敛性,取某栋建筑物迭代过程中的中间值作为建筑物高与真实建筑物高求取高程误差,该误差随着迭代次数的变化趋势如图 12所示,从图 12中可以看出误差值随着迭代计算而变小,并逐渐趋近于零,在第6次迭代后误差值已变为厘米级,该变化趋势表明本文算法具有较好的收敛性。
|
| 图 11 檐口高初始值与精确值误差对比 Fig. 11 Comparison of Initial Eaves Height and Precision Eaves Height |
|
| 图 12 误差随迭代次数的变化趋势 Fig. 12 Variation Trend of Error with Iteration |
本文提出了一种对二维线划图中建筑物进行全自动檐口高提取的方法,首先提出了一种基于极大值边缘信息量的高程初值提取方法,在此基础上通过数据准备和精确值求解过程,利用广义点摄影测量理论求取精确檐口高。实验结果表明,该方法可有效提取建筑物檐口高,并具有较好的测量精度。该方法在建筑物批量自动化三维建模、人工地物的自动提取等方面也有较大应用价值,其计算过程可扩展至其他具有CAD数据的目标物体测量中。
| [1] | Zhang Jianqing, Pan Li, Wang Shugen. Photogrammetry[M]. Wuhan:Wuhan University Press, 2003(张剑清,潘励,王树根.摄影测量学[M].武汉:武汉大学出版社,2003) |
| [2] | Fan Jiuguo. Research on Three-Dimensional Digital Terrain Mapping Technology[D]. Xi'an:Xi'an University of Science and Technology,2009(范玖国. 三维数字地形图测绘技术的研究[D].西安:西安科技大学,2009) |
| [3] | Pan Zhengfeng, Yang Zhengyao, Cheng Xiaojun, et al. Principles and Methods of Digital Mapping[M].Wuhan:Wuhan University Press, 2004(潘正风, 杨正尧, 程效军, 等. 数字测图原理与方法[M].武汉:武汉大学出版社, 2004) |
| [4] | Liu Xiaohui, Wu Yundong. Application of VLL to Obtaining the Elevation of Constructions[J].Engineering of Surveying and Mapping,2006(1):70-72+78(刘晓辉,吴云东.VLL方法在自动获取建筑物高程中的应用[J].测绘工程,2006(1):70-72+78) |
| [5] | Yang Yongchong, Hu Nan, Guo Lan. On Surveying and Mapping Technology for 3D Digital Topographic Map[J].Bulletin of Surveying and Mapping,2011(1):75-77(杨永崇,胡楠,郭岚. 三维数字地形图测绘技术研究[J].测绘通报,2011(1):75-77) |
| [6] | Cheng F, Thiel K H. Delimiting the Building Heights in a City from the Shadow in a Panchromatic SPOT-Image-Part 1. Test of Forty-Two Buildings[J]. Remote Sensing, 1995, 16(3):409-415 |
| [7] | Shettigara V K, Sumerling G M. Height Determination of Extended Objects Using Shadows in SPOT Images[J]. Photogrammetric Engineering and Remote Sensing, 1998, 64(1):35-43 |
| [8] | Shao Y, Taff G N, Walsh S J. Shadow Detection and Building-Height Estimation Using IKONOS DATA[J]. International Journal of Remote Sensing, 2011, 32(22):6929-6944 |
| [9] | Comber A, Umezaki M, Zhou R, et al. Using Shadows in High-Resolution Imagery to Determine Building Height[J]. Remote Sensing Letters, 2012, 3(7):551-556 |
| [10] | Zhang Zuxun, Wu Jun, Zhang Jianqing. A Method for Determining Orientation Parameters in Image-based Reconstruction of Architectural Scenes[J]. Geomatics and Information Science of Wuhan University, 2003, 28(3):265-271(张祖勋, 吴军, 张剑清. 建筑场景三维重建中影像方位元素的获取方法[J]. 武汉大学学报·信息科学版, 2003, 28(3):265-271) |
| [11] | Liu Yanchun, Chen Lun, Song Weidong. Research on the Method of single Image Building Measuring Based on Vanishing Point[J]. Engineering of Surveying and Mapping, 2008, 17(1):71-74(刘艳春, 陈轮, 宋伟东. 基于灭点的单片规则建筑物三维重建方法研究[J]. 测绘工程, 2008, 17(1):71-74) |
| [12] | Shufelt J A. Performance Evaluation and Analysis of Vanishing Point Detection Techniques[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21(3):282-288 |
| [13] | Zhang Zuxun, Zhang Jianqing. Generalized Point Photogrammetry and Its Application[J]. Geomatics and Information Science of Wuhan University, 2005, 30(1):1-5(张祖勋, 张剑清. 广义点摄影测量及其应用[J]. 武汉大学学报·信息科学版, 2005, 30(1):1-5) |
 2016, Vol. 41
2016, Vol. 41



