文章信息
- 郭忠磊, 翟京生, 邓凯亮
- GUO Zhonglei, ZHAI Jingsheng, DENG Kailiang
- 基于LM方法的大姿态角影像空间后方交会
- Space Resection of Big Attitude Image Based on Levenberg-Marquardt Method
- 武汉大学学报·信息科学版, 2016, 41(4): 565-568
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 565-568
- http://dx.doi.org/10.13203/j.whugis20130706
-
文章历史
- 收稿日期: 2014-11-25

2. 天津海洋测绘研究所, 天津, 300061
2. Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China
目前,低空无人机平台已逐渐应用到专业摄影测量领域。共线方程是解算影像外方位元素的基础模型,通常采用经典的Gauss-Markov(高斯-马尔可夫模型)迭代求解[1]。低空遥感平台由于自身的结构特点,难以提供稳定的姿态。在大姿态角摄影时,江刚武[2]、闫利[3]等采用单位四元数代替欧拉角构建影像的共线方程,实现空间后方交会模型的收敛解算;周拥军[4]采用单位四元数代替欧拉角(Euler Angle)实现了大姿态角条件下的相对定向模型解算。然而,由于单位四元数之间存在相关性,基于单位四元数建立的空间后方交会解算模型需采用附有约束条件的间接平差方法,降低了算法的稳定性和实用性。
Levenberg-Marquardt(LM)方法的优点是能够克服法方程系数矩阵病态时迭代过程出错或初值不当导致不收敛的问题[5, 6, 7, 8, 9]。本文采用LM方法,对大姿态角下影像的空间后方交会模型进行解算,通过模拟数据验证了该方法在影像外方位元素初值与真值偏差较大时,影像的外方位元素仍能实现可靠解算。
1 空间后方交会几何模型影像外方位元素描述了相机的透视中心点在物方坐标系中的位置及像空间坐标系在物方坐标系中的角方位元素,一般由三个线方位元素(XS,YS,ZS)和三个独立的角方位元素(φ,ω,κ)表示。共线条件方程是摄影测量数据处理的理论基础,是诸如单像空间后方交会等一系列原理的出发点[10]。根据摄站点、像点、物点三点共线几何关系有:
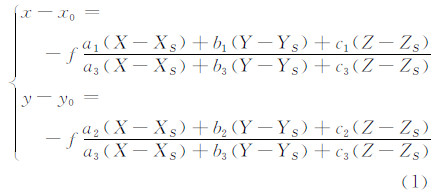
式中,(x,y,-f)为像点的像空间坐标;(x0,y0)为主点的像平面坐标;f为像片的主距;ai、bi、ci(i=1,2,3)是由三个外方位角元素求得的方向余弦值。
共线条件方程是影像外方位元素的非线性函数,采用泰勒级数展开,取一次项进行线性化得误差方程的矩阵形式:

式中,
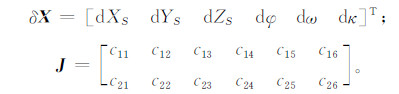
空间后方交会几何模型是一个非线性方程,一般需采用迭代的方法解算参数[11]。如果迭代参数的初始值与真值的偏差过大,迭代收敛速度较慢,甚至可能不收敛。对于大姿态角下的摄影影像,需要考虑不依赖初值的参数求解方法。
2 空间后方交会无初值依赖解算法 2.1 基于单位四元数的空间后方交会基于单位四元数[2, 3]表示的共线方程按泰勒级数展开,误差方程写为矩阵形式与式(2)一致:
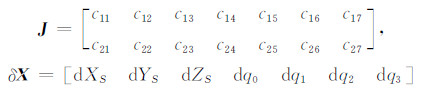
由于采用单位四元数q表示影像的姿态参数,单位四元数表示的误差方程存在约束条件:
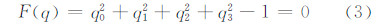
基于单位四元数的空间后方交会算法需利用带有附加条件的间接平差模型进行平差求解。常规解算方法采用高斯-牛顿(Gauss-Newton,GN)迭代解算外方位元素时,需要假定其雅可比(Jacobi)迭代矩阵在迭代过程中是满秩的,在雅可比迭代矩阵是秩亏或者严重病态时,数值迭代方法面临失效的情况。
2.2 Levenberg-Marquardt方法在数学运算中,LM方法又称为阻尼最小二乘法(damped least-squares,DLS)。DLS最早由Levenberg[12]于1944年提出,但在当时没有受到重视,后来Marquardt[6]又重新提出,并在理论上进行了探讨。所以,DLS算法被称为Levenberg-Marquardt方法。LM主要用于解决非线函数在参数空间中的最小值问题,类似于其他的数值最小化算法,LM对参数的求解也需要迭代。
Levenberg的贡献是将GN公式中法方程系数阵N=JTJ的对角元素增加一个阻尼因子,非负的阻尼因子λ在每次迭代过程中对系数阵N+λI进行调整。Levenberg算法的不足是当阻尼因子λ过大时,N+λI的逆矩阵产生失真现象。Marquardt提出对系数阵的每一个对角元素乘以阻尼因子,可保证梯度较小时代价函数沿梯度方向仍有较大的变化。Levenberg提出的公式为:
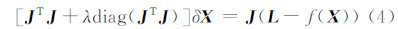
式中,f(X)表示由初始参数X计算的函数值。
实际应用中,基于LM方法的参数估计公式为:
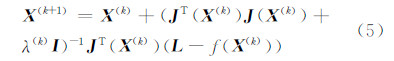
式中,k=1,2,…,n,为迭代的次数;I为单位阵;阻尼因子λ的选择与Levenberg的方法不同,结合了Levenberg与Marquardt对阻尼参数选择的原理,初始赋值:
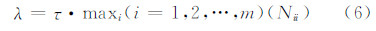
式中,τ=0.001;i=1,2,…,m,表示参数估计的个数;Nii表示法方程系数矩阵对角元素。
参数迭代解算过程中需要不断更新阻尼因子。LM方法保证了参数的全局收敛性。克服迭代矩阵病态时迭代过程出错或初值不当导致不收敛的主要方法通过阻尼参数λ进行调整实现。代价函数减小过快时,则会选择一个较小的阻尼因子,此时阻尼最小二乘近似于GN迭代;如果迭代过程中代价函数值减小太少,阻尼因子增大,提供一个梯度下降的方向保证代价函数向着减小的方向移动,具有近似线性收敛速度。所以,LM方法比GN方法稳健,即使初值严重偏离真值也能得到最优解。对具有合理起始参数的良性函数,LM方法的计算收敛速度要比GN方法的慢,LM方法也被视为参数在信赖域中的GN方法。
如果观测值的不确定性用协方差变量Σ表示,则权阵P=Σ-1,法方程表示为:
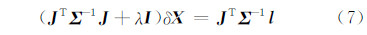
式中,l表示向量残差。参数解算过程不变。阻尼因子决定着参数的迭代实现过程,目前常用的阻尼因子的更新方式主要有两种。
LM1方法:给定阻尼因子初始值λ=10-3,计算δX使得误差减少,接受该参数增量δX,在下一次迭代之前将λ除以10;否则将阻尼因子乘以10,重新解算增量正规方程。
LM2方法:阻尼因子λ由式(6)赋初值,阻尼因子与参数增量的更新由代价函数的增量比例控制,如式(8)所示:

如果ρ>0,接受参数增量δX并更新参数值。此时阻尼因子更新为:
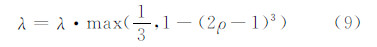
否则,拒绝参数增量δX,阻尼因子更新为λ=λ·v,v=2·v(v初值为2),重新估计δX。
3 算例与分析空间后方交会计算外方位元素时,至少需要知道三个地面控制点的大地坐标及其对应的像点坐标。控制点可以是实地外业测量的结果,也可以是摄影测量加密或其他方式得到的成果。算法验证采用文献[2]中的仿真数据,给定9个均匀分布的地面控制点,如图 1所示。

|
| 图 1 控制点的分布 Fig. 1 Distribution of the Control Points |
提供三组影像(IMG_4、IMG_5、IMG_6)的外方位元素,具体见表 1;依据共线条件方程式(1)模拟控制点对应的像点坐标。采用欧拉角表示的空间后方交会模型,设观测值的权阵为单位阵,分别采用GN、LM1、LM2计算模拟数据的外方位元素。角度限差通常为0.1′[13],在此保留至0.01′(约为1.67°×10-4)。计算结果与文献[2]中基于单位四元数的无初值依赖空间后方交会方法比较,如表 2所示。
| 真值 | 外方位线元素/m | 外方位角元素/(°) | ||||
| XS | YS | ZS | φ | ω | κ | |
| IMG_4 | 1 620 | 1 620 | 2 250 | -1.666 7 | 1.166 7 | 0.333 3 |
| IMG_5 | 1 620 | 1 620 | 2 250 | 20.0 | 30.0 | 40.0 |
| IMG_6 | -1 620 | -1 620 | 2 250 | 80.0 | 80.0 | 40.0 |
| 方法 | 参数 | 外方位线元素/m | 外方位角元素/(°) | 迭代次数 | 备注 | ||||
| XS | YS | ZS | φ | ω | κ | ||||
| Gauss-Newton (GN) | IMG_4 | 1 620 | 1 620 | 2 250 | -1.666 7 | 1.166 7 | 0.333 3 | 5 | √ |
| IMG_5-9 | × | × | × | × | × | × | - | × | |
| IMG_5-6 | 1 620 | 1 620 | 2 250 | 20.0 | 30.0 | 40.0 | 8 | √ | |
| IMG_6 | × | × | × | × | × | × | 26 | × | |
| Levenberg- Marquart 1(LM1) | IMG_4 | 1 620 | 1 620 | 2 250 | -1.666 7 | 1.166 7 | 0.333 3 | 11 | √ |
| IMG_5-6 | 1 620 | 1 620 | 2 250 | 20.0 | 30.0 | 40.0 | 12 | √ | |
| IMG_6 | -1 620 | -1 620 | 2 250 | 80.0 | 80.0 | 40.0 | 21 | √ | |
| Levenberg- Marquart 2(LM2) | IMG_4 | 1 620 | 1 620 | 2 250 | -1.666 7 | 1.166 7 | 0.333 3 | 17 | √ |
| IMG5-6 | 1 620 | 1 620 | 2 250 | 20.0 | 30.0 | 40.0 | 18 | √ | |
| IMG_6 | -1 620 | -1 620 | 2 250 | 80.0 | 80.0 | 40.0 | 32 | √ | |
| 基于单位四元 数的空间 后方交 会[2] | IMG_4 | 1 620 | 1 620 | 2 250 | -1.666 7 | 1.166 7 | 0.333 3 | 6 | √ |
| IMG_5 | 1 620 | 1 620 | 2 250 | 20.0 | 30.0 | 40.0 | 21 | √ | |
| IMG_6 | -1 620 | -1 620 | 2 250 | 80.0 | 80.0 | 40.0 | 29 | √ | |
分析表 2的结果可得出以下结论。
1)在大姿态角条件下,从迭代效率方面比较,LM解算欧拉角表示的空间交会模型要优于基于单位四元数的无初值依赖的空间后方交会模型参数解算。
2)对文献[2]中的模拟数据进行解算,IMG_4在较小的姿态下采用GN、LM方法均收敛;而IMG_5在9个点参与解算时均发散。分析发现,原始数据IMG_5的前3个控制点虽然满足共线条件模型,但严重失真,将其视为粗差删除后仿真数据变为IMG_5-6,此时迭代过程收敛;IMG_6由于初值严重偏离真实值,GN解算发散,而LM1、LM2则可实现收敛。
3)比较LM1与LM2方法,阻尼因子的不同影响迭代的效率。
4 结语低空无人机遥感是介于常规航空摄影测量与近景摄影测量之间的一种摄影作业模式,计算机视觉领域中的模型算法可用于处理低空无人机影像数据,具有一定的应用前景。相比GN迭代过程及基于单位四元数的空间后方交会模型,附加阻尼因子的LM方法从模型解算方法上实现了对初值选择的无依赖性,具有与单位四元数法相当的可靠性和稳定性。通过选择合适的阻尼因子,LM法迭代效率更高。但是,相比GN迭代法,LM方法需要更多的迭代次数,下一步将对优化迭代次数的方法进行研究。
| [1] | Chen Yi, Lu Yu, Zheng B O. Application of Total Least Squares to Space Resection[J]. Geomatics and Information Science of Wuhan University, 2008, 33(12):1271-1274(陈义, 陆珏, 郑波. 总体最小二乘方法在空间后方交会中的应用[J]. 武汉大学学报·信息科学版,2008,33(12):1271-1274) |
| [2] | Jiang Gangwu, Jiang Ting, Wang Yong, et al. Space Resection Independent of Initial Value Based on Unit Quaternions[J]. Acta Geodaetica et Cartographica Sinica, 2007,36(2):169-175(江刚武,姜挺,王勇,等.基于单位四元数的无初值依赖空间后方交会[J].测绘学报,2007,36(2):169-175) |
| [3] | Yan Li, Nie Qian, Zhao Zhan. Space Resection of Line Scanner CCD Image Based on the Description of Quaternions[J]. Geomatics and Information Science of Wuhan University, 2010,35(2):201-204(闫利, 聂倩, 赵展. 利用单位四元数描述线阵CCD影像的空间后方交会[J]. 武汉大学学报·信息科学版,2010,35(2):201-204) |
| [4] | Zhou Yongjun, Deng Caihua. A New Method for Relative Orientation with Hybrid Genetic Algorithm and Unit Quaternion[J]. Geomatics and Information Science of Wuhan University, 2011,36(6):670-673(周拥军,邓才华. 利用HGA和单位四元数的相对定向解法[J]. 武汉大学学报·信息科学版, 2011, 36(6):670-673) |
| [5] | Manolis I, Lourakis A, Antonis A. Argyros Sba:A Software Package for Generic Sparse Bundle Adjustment[J]. ACM Transactions on Mathematical Software, 2009,36(1):1-30 |
| [6] | Marquardt D. An Algorithm for the Least-squares Estimation of Nonlinear Parameters[J]. SIAM J. Appl. Math, 1963,11(2):431-441 |
| [7] | Kelley C T. Iterative Methods for Optimization[M]. Philadelphia:SIAM Society for Industrial and Applied Mathematics,1999:324-335 |
| [8] | Hartley R, Zisserman A. Multiple View Geometry in Computer Vision[M]. 1st ed. Cambridge:Cambridge University Press, 2000 |
| [9] | Madsen K, Nielsen H, Tingleff O. Methods for Non-linear Least Squares Problems[OL]. http://www.imm.dtu.dk/pubdb/views/edoc_download.php/3215/pdf/imm3215.pdf,2004 |
| [10] | Wang Zhizhuo. The Principles of Photogrammetry[M]. Wuhan:Wuhan Uniersity Press,2007(王之卓. 摄影测量原理[M].武汉:武汉大学出版社,2007) |
| [11] | Tang Limin. Research on the Ill-posed and Solving Methods of Nonlinear Least Squares Problem[D].Changsha:Central South University,2011(唐利民.非线性最小二乘问题的不适定性及算法研究[D].长沙:中南大学,2011) |
| [12] | Levenberg K. A Method for the Solution of Certain Non-linear Problems in Least Squares[J]. Quart Appl. Math, 1944,2(2):164-168 |
| [13] | Wang Peijun, Xu Yaming. The Photogrammetry[M].Wuhan:Wuhan Uniersity Press,2007(王佩军, 徐亚明. 摄影测量学[M].武汉:武汉大学出版社,2007) |
 2016, Vol. 41
2016, Vol. 41


