文章信息
- 吕志鹏, 伍吉仓, 公羽
- LV Zhipeng, WU Jicang, GONG Yu
- 利用四元数改进大旋转角坐标变换模型
- Improvement of a Three-dimensional Coordinate Transformation Model Adapted to Big Rotation Angle Based on Quaternion
- 武汉大学学报·信息科学版, 2016, 41(4): 547-553
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 547-553
- http://dx.doi.org/10.13203/j.whugis20140171
-
文章历史
- 收稿日期: 2014-10-10

2. 国家知识产权局专利局专利审查协作江苏中心, 江苏 苏州, 215163
2. Patent Examination Cooperation Jiangsu Center of the Patent Office, SIPO, Suzhou 215163, China
四元数的概念最早由Hamilton于1843年提出,目的是在空间矢量的研究中找到类似解决平面问题时使用的复数方法[1]。四元数的提出首先在捷联式惯性导航、人造卫星姿态控制、多体系统力学等位置与姿态的控制领域得到广泛应用[2, 3, 4, 5]。近年来,四元数在图像特征提取、图像检索、图像分割、图像边缘检测等图形学领域的应用越来越广泛[6, 7, 8]。而在测绘领域,四元数主要应用于摄影测量解算、数字图像处理、大地坐标变换等方面[9, 10]。对于微小角度的坐标变换,Bursa-Wolf模型、Molodensky模型等线性模型已经被广泛采用,并且取得了良好的变换结果。然而,对于大旋转角的三维坐标变换,上述模型并不适用。为此,文献[11]将方向余弦矩阵作为旋转矩阵,并对三维坐标变换模型进行线性化,适用于任意角度的旋转。文献[12]用四元数构造旋转矩阵,然后对三维坐标变换模型进行线性化,解决了大旋转角三维坐标变换问题。文献[13]用欧拉角表示旋转矩阵并对三维坐标变换模型进行线性化,同样取得了良好的结果。文献[14]通过将遗传算法应用到三维坐标变换并且将旋转矩阵用Lodrigues矩阵进行表示,构造了一种直接搜索算法。本文立足于基于四元数的大旋转角坐标变换模型,考虑到该迭代算法严重依赖于初值的选取,利用定姿算法[15, 16, 17, 18]确定该算法旋转参数初值,增强了该算法的稳健性。
1 实四元数与三维旋转变换的关系实四元数是一种四元矢量,若a、b、c、d均为实数,那么定义a+bi+cj+dk为实四元数。其中i、j、k为广义虚部,它们满足关系式:
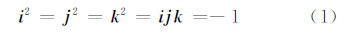
由式(1)可以推出:
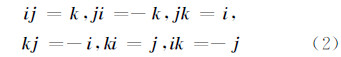
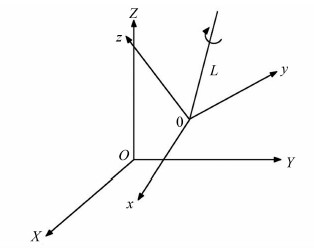
实四元数的运算性质符合相应的复数运算法则[5]。同时,定义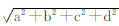 为上述实四元数的模,若其等于1,则称此实四元数为单位实四元数。对于任意一个三维向量v=(x,y,z),令其与一个实四元数V=0+xi+yj+zk对应。至此,将三维向量空间与实四元数建立起一一对应的关系。如图 1所示,两组空间直角坐标之间进行三维旋转变换,不仅可以看成其中一个坐标系绕着它的三个坐标轴的旋转,也可以看成是绕过其原点的某定轴L的旋转。假设L的单位向量为n=(n1,n2, n3),那么绕L旋转θ角度的旋转变换可以用单位实四元数表示[15]:
为上述实四元数的模,若其等于1,则称此实四元数为单位实四元数。对于任意一个三维向量v=(x,y,z),令其与一个实四元数V=0+xi+yj+zk对应。至此,将三维向量空间与实四元数建立起一一对应的关系。如图 1所示,两组空间直角坐标之间进行三维旋转变换,不仅可以看成其中一个坐标系绕着它的三个坐标轴的旋转,也可以看成是绕过其原点的某定轴L的旋转。假设L的单位向量为n=(n1,n2, n3),那么绕L旋转θ角度的旋转变换可以用单位实四元数表示[15]:
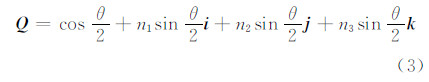
|
| 图 1 三维旋转变换 Fig. 1 3D Rotation Transformation |
对于任意一个三维向量v,由文献[15]可知:

式中,U为v进行旋转变换后得到的新向量u所对应的实四元数;Q-1为单位实四元数Q的逆:

因此,用实四元数表达坐标旋转变换,关键在于确定单位实四元数Q。
2 三维坐标变换的数学模型根据三维坐标变换的几何意义可得其数学模型:
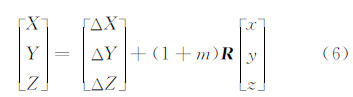
式中,(x,y,z)是原坐标系下的坐标;(X,Y,Z)是目标坐标系下的坐标;(ΔX,ΔY,ΔZ)是原坐标系o-xyz原点在目标坐标系O-XYZ下的坐标,即为三维坐标变换的平移参数;m是三维坐标变换的尺度变化因子;R是三维坐标变换的旋转矩阵。
假设三维旋转变换对应的单位实四元数为Q=q0+q1i+q2j+q3k,将其代入式(4)并整理,可得由单位实四元数Q的分量表示的旋转矩阵:
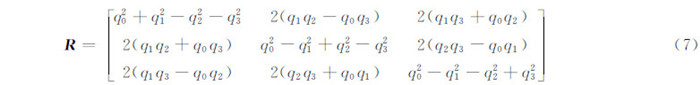
旋转矩阵R中的四个参数中只有三个是独立的。因为旋转矩阵所对应的实四元数是单位实四元数,故有:
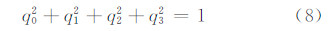
将式(8)在其近似值处进行泰勒展开并保留至一次项,可得:

在此,设u=1+m为尺度因子。式中,上标为0的符号表示相应模型参数的近似值;dΔX、dΔY、dΔZ、du、dq0、dq1、dq2、dq3为模型参数的改正数。将式(9)改写成误差方程的形式:

式中,


对于三维坐标变换,如果有三个或三个以上的公共点,应用最小二乘原理可以得到式(6)、(8)的最优解。但由于旋转矩阵R的非线性特性,用牛顿法迭代求解式(6)、式(8)。根据式(8)可以列出限制条件方程:

式中,A=(0 0 0 0 2q00 2q10 2q20 2q30);W=q002+q102+q202+q302-1; 意义与式(10)中相同。为了提高数值计算的稳定性,将限制条件方程转换为伪观测方程:
意义与式(10)中相同。为了提高数值计算的稳定性,将限制条件方程转换为伪观测方程:
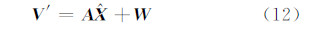
联立式(10)、(12)按间接平差法进行迭代计算,可以得到模型参数。模型参数估值表达式如下:

式中,P为目标坐标系下坐标(X,Y,Z)的权阵(对于伪观测值的权应该赋以较大的值);C= ;NCC=CΤPC。然后,更新转换参数初值重复上述参数求解过程。如此重复迭代直至
;NCC=CΤPC。然后,更新转换参数初值重复上述参数求解过程。如此重复迭代直至 向量满足迭代收敛条件。至此,我们构造了运用牛顿法计算三维坐标变换参数的数学模型。三维坐标变换的内符合精度可以用平差的验后单位权中误差评定:
向量满足迭代收敛条件。至此,我们构造了运用牛顿法计算三维坐标变换参数的数学模型。三维坐标变换的内符合精度可以用平差的验后单位权中误差评定:
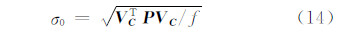
式中,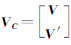 。如果有n个公共点,则平差的自由度f=3n-7。对于外符合精度的评定,均匀选择部分公共点,不参加坐标转换参数的求解,然后利用求得的转换参数进行转换,将转换的结果与已知坐标进行比较,求得差值或RMS。
。如果有n个公共点,则平差的自由度f=3n-7。对于外符合精度的评定,均匀选择部分公共点,不参加坐标转换参数的求解,然后利用求得的转换参数进行转换,将转换的结果与已知坐标进行比较,求得差值或RMS。
牛顿法迭代计算过程如下:① 选取模型参数的迭代初值。② 将模型参数近似值代入式(10)、式(12)构造误差方程和伪观测方程。③ 根据式(13)计算模型参数的新值 (k+1)(k为迭代计算次数)。④ 检验迭代计算的模型参数新值
(k+1)(k为迭代计算次数)。④ 检验迭代计算的模型参数新值 (k+1)是否满足收敛条件(本文设平移参数迭代误差小于1 mm,尺度因子迭代误差小于10-7,单位四元数各分量的迭代误差小于10-7为收敛条件),如果不满足收敛条件就以其为参数近似值重复步骤②~③;如果满足收敛条件就利用这组模型参数将原坐标系下的坐标变换到目标坐标系下完成坐标变换过程。
(k+1)是否满足收敛条件(本文设平移参数迭代误差小于1 mm,尺度因子迭代误差小于10-7,单位四元数各分量的迭代误差小于10-7为收敛条件),如果不满足收敛条件就以其为参数近似值重复步骤②~③;如果满足收敛条件就利用这组模型参数将原坐标系下的坐标变换到目标坐标系下完成坐标变换过程。
牛顿法是一种局部收敛的数值计算方法,它对未知参数的初值有很强的依赖性。初值较差时,有可能出现收敛于局部最优解或迭代不收敛的现象。因而,本文构造如下数学模型计算迭代初值,设:

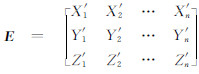 ;U=
;U= ;M为旋转矩阵初值。
;M为旋转矩阵初值。
E、U中的n为公共点个数。E、U中各元素为公共点中心化后的坐标,即由各坐标分量减去所其对应的重心坐标分量。
将式(15)变型得:
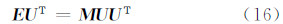
因为U为行满秩矩阵,式(15)中方程右边UUT为满秩矩阵,据此可以计算出旋转矩阵初值M[10]。进而可以从旋转矩阵初值M中提取其所对应的单位四元数初值。从旋转矩阵中提取四元数的算法已经很成熟[16, 17, 18],在此运用文献[18]中的算法进行提取。首先根据旋转矩阵初值M构造矩阵K:
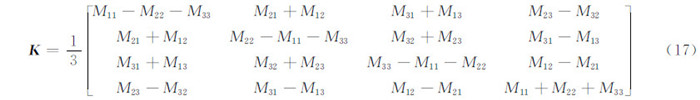
然后计算矩阵K最大特征值对应的特征向量D=(d1,d2,d3,d4),则单位四元数的初值为:
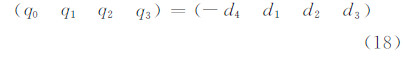
为了与其他有关大旋转角三维坐标变换的文献[11, 13]结果进行比较,本文采用文献[11]中广州新机场航站楼网架中一个构件的节点坐标数据。在这个实例中目标坐标系(设计坐标系)轴的指向为X向北、Z向东、Y向上,原点为构件端点铰的中心。原坐标系(测量坐标系)轴的指向为x向北、y向东、z向上,原点任意假设。采用本文提出的算法,17个公共点全部参加三维坐标变换的计算,经过5次迭代得到尺度因子为u=1.002 025 373 4,平移参数为(ΔX,ΔY,ΔZ)=(-109 110.147,-101 334.649,-96 486.682),旋转矩阵为:
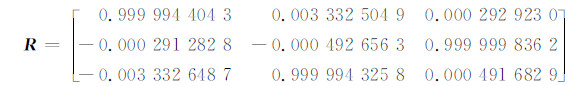
单位权中误σ0=8.16 mm。同时,采用将文献[11]中的条件方程转换为伪观测方程的方法,利用其数学模型计算三维坐标变换参数,并且利用文献[13] 计算三维坐标变换参数。
利用本文算法和文献[11, 13]中算法完成三维坐标变换,并将实测的坐标转换为设计坐标,与已知设计坐标的较差如图 2所示。从图 2中可知,利用本文算法计算的X、Y、Z方向的坐标较差与文献 [11]、[13]中的算法计算的坐标较差互差绝大部分都保持在3 mm以内。这说明三种算法具有很好的一致性。同时,两种算法计算的坐标较差结果也主要集中在10 mm以内,反映出各种算法对数据均具有很好的拟合。

|
| 图 2 各种算法的坐标较差 Fig. 2 Coordinate Difference of Various Algorithms |
表 1列出了利用本文算法和文献[11, 13]中算法根据17个公共点计算得到的三维坐标变换的迭代次数。本文引入的初值构造算法显著减少了迭代次数。同时,文献[11, 13]采用如下够造算法,即:

通过三种算法迭代次数的比较可知,文献[11]算法对初值依赖程度较小,文献[13]算法使用式(19)的初值迭代次数显著增加,对初值的依赖性增强。而通过本文引入的初值构造方法保证基于四元数的大旋转角三维坐标变换算法的稳健性。
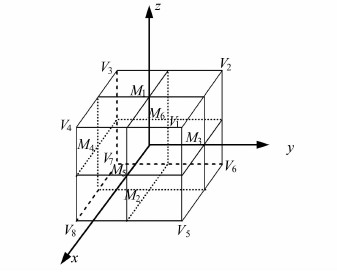
3.2 算例二算例二中的数据改编自文献[14]。其中,旧坐标系下的坐标对应于以坐标原点为中心的立方体各顶点坐标以及正方体各表面中点坐标,如图 3所示。而新坐标系下的坐标是将上述坐标分沿x、y、z轴方向平移1 000 m、2 000 m、3 000 m后,再绕x、y、z轴旋转30°、45°、60°之后得到,具体见表 2。
|
| 图 3 模拟算例 Fig. 3 Simulation Example |
| 点号 | 旧坐标系下的坐标 | 新坐标系下的坐标 | ||||
| x | y | z | X | Y | Z | |
| V1 | 2 000 | 2 000 | 2 000 | 3 814.313 | 2 589.568 | 4 931.852 |
| V2 | -2 000 | 2 000 | 2 000 | 2 400.100 | 5 039.058 | 2 103.425 |
| V3 | -2 000 | -2 000 | 2 000 | -1 307.007 | 4 531.752 | 3 517.638 |
| V4 | 2 000 | -2 000 | 2 000 | 107.206 | 2 082.262 | 6 346.065 |
| V5 | 2 000 | 2 000 | -2 000 | 3 307.007 | -531.752 | 2 482.362 |
| V6 | -2 000 | 2 000 | -2 000 | 1 892.794 | 1 917.738 | -346.065 |
| V7 | -2 000 | -2 000 | -2 000 | -1 814.313 | 1 410.432 | 1 068.148 |
| V8 | 2 000 | -2 000 | -2 000 | -400.100 | -1 039.058 | 3 896.575 |
| M1 | 0 | 0 | 2 000 | 1 253.653 | 3 560.660 | 4 224.745 |
| M2 | 0 | 0 | -2 000 | 746.347 | 439.340 | 1 775.255 |
| M3 | 0 | 2 000 | 0 | 2 853.553 | 2 253.653 | 2 292.893 |
| M4 | 0 | -2 000 | 0 | -853.553 | 1 746.347 | 3 707.107 |
| M5 | 2 000 | 0 | 0 | 1 707.107 | 775.255 | 4 414.214 |
| M6 | -2 000 | 0 | 0 | 292.893 | 3 224.745 | 1 585.786 |
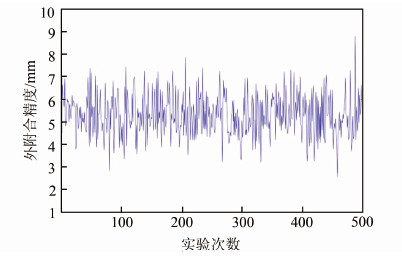
对新坐标系下的坐标加上标准差σ=5 mm的高斯白噪声扰动。首先,选取旧坐标系下立方体8个顶点及其相对应的新坐标系下的坐标作为三维坐标变换的公共点,利用本文算法进行坐标变换并评定坐标变换的内符合精度。然后,利用在旧坐标系下立方体6个表面中点的坐标,根据求定的坐标变换参数转换为新坐标系下的坐标,并与已知坐标进行比较,得到坐标变换的外符合精度。为了保证数值实验的可靠性,对此模拟实验重复500次,每次随机产生高斯白噪声序列,得到模拟观测值。各次模拟实验计算的三维坐标转换的内符合精度和外符合精度如图 4、5所示。

|
| 图 4 内符合精度 Fig. 4 Inner Precision |
|
| 图 5 外符合精度 Fig. 5 External Precision |
通过对图 4、5进行观察可知,各次模拟实验计算得到的坐标变换内符合精度和外符合精度也呈现出随机特性。对各次模拟实验的内符合精度求均值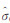 0=3.5 mm,构造χ2统计量对平差模型进行检验。原假设和备择假设为:
0=3.5 mm,构造χ2统计量对平差模型进行检验。原假设和备择假设为:

统计量数值为:

设显著性水平为5%,查χ2分布表[19]得置信区间为(6.908,28.845),统计量数值落入置信区间。因而,本文算法通过模型正确性的检验,平差模型正确,平差结果具有可靠性。此外,我们对外符合精度求均值,其值为5.3 mm,与噪声水平相当。故在测区范围内均匀选择若干公共点利用本文算法进行三维坐标变换[20],理论上可以得到与测量噪声水平相当的坐标转换精度。
4 结 语本文将三维旋转变换矩阵用四元数进行表示,构造了基于四元数的三维坐标变换模型,并且推导了其牛顿法迭代法计算的线性模型。由于该迭代算法依赖于初值的选取,本文引入了一种获取迭代初值的方法,确保了基于四元数的三维坐标变换模型的稳健性。相对于用方向余弦和欧拉角构造的三维旋转变换矩阵,实四元数几何意义更加直观,并且数值计算稳定,易于编程计算,计算效率高。本文算法适合任意角度的旋转,也适合左右手坐标系的变换。可以应用于大地测量、摄影测量等领域的坐标变换。应用四元数构造旋转变换矩阵进行三维坐标变换是四元数在测绘领域的一个重要应用,同时,四元数在摄影测量解算、数字图像处理等领域应用前景广泛。
| [1] | Hamilton S W R. On Quaternions; or on a New System of Imaginaries in Algebra[J]. Philosophical Magazine, 2009, 29(191):425-439 |
| [2] | Xiao Shangbin. Quaternion Method and Application[J]. Advances in Mechanics, 1993, 23(2):249-260(肖尚彬. 四元数方法及应用[J]. 力学进展, 1993, 23(2):249-260) |
| [3] | Zhang Ronghui, Jia Hongguang, Chen Tao, et al. Attitude Solution for Strapdown Inertial Navigation System Based on Quaternion Algorithm[J]. Optics and Precision Engineering, 2008, 16(10):1965-1970(张荣辉, 贾宏光, 陈涛, 等. 基于四元数法的捷联式惯性导航系统的姿态解算[J]. 光学精密工程, 2008, 16(10):1965-1970) |
| [4] | Jiang Rui, Wei Jiaolong, Cen Zhaohui. Simulation Modelling of Satellite Attitude Control System Based on Quaternion Feedback[J]. Journal of System Simulation, 2009, 21(19):6260-6265(蒋睿, 魏蛟龙, 岑朝辉. 基于四元数反馈的卫星姿态控制系统仿真模型建立[J]. 系统仿真学报, 2009, 21(19):6260-6265) |
| [5] | Branets V N, Shmyglevsky I P. Application of Quaternion in Rigid Body[M]. Liang Zhenhe, Trans. Wang Chaoqun, Proof. Beijing:National Defense Industry Press, 1977:9-17(B.H.勃拉涅茨, И.П.施梅格列夫斯基著. 四元数在刚体定位中的应用[M]. 梁振和译, 汪朝群校. 北京:国防工业出版社, 1977:9-17) |
| [6] | Cui Feng, Cao Xueguang, Peng Silong. A New Phase Definition of Quaternionic Analytic Signal[J]. Journal of Image and Graphics, 2006, 11(2):251-258(崔峰, 曹学光, 彭思龙. 新的四元数解析信号相位定义[J]. 中国图象图形学报, 2006, 11(2):251-258) |
| [7] | Ran Ruisheng, Huang Yanzhu. The Recognition of Color Images Based on the Singular Value Decompositions of Quaternion Matrices[J]. Computer Science, 2006, 33(7):227-229(冉瑞生, 黄廷祝. 基于四元数矩阵奇异值分解的彩色图像识别[J]. 计算机科学, 2006, 33(7):227-229) |
| [8] | Lang Fangnian, Zhou Jiliu, Yan Bin, et al. Quaternion and Color Image Edge Detection[J]. Computer Science, 2007, 34(11):212-216(郎方年, 周激流, 闫斌, 等. 四元数与彩色图像边缘检测[J]. 计算机科学, 2007, 34(11):212-216) |
| [9] | Guan Yunlan, Cheng Xiaojun, Zhou Shijian, et al. A Solution to Space Resection Based on Unit Quaternion[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1):30-35(官云兰, 程效军, 周世健, 廖中平, 鲁铁定. 基于单位四元数的空间后方交会解算[J]. 测绘学报, 2008, 37(1):30-35) |
| [10] | Shen Y Z, Chen Y, Zheng D H. A Quaternion-Based Geodetic Datum Transformation Algorithm[J]. Journal of Geodesy, 2006, 80:233-239 |
| [11] | Chen Yi, Shen Yunzhong, Liu Dajie. A Simplified Model of Three Dimensional Datum Transformation Adapted to Big Rotation Angle[J]. Geomatics and Information Science of Wuhan University, 2004, 29(12):1101-1105(陈义, 沈云中, 刘大杰. 适合于大旋转角的三维基准变换的一种简洁模型[J]. 武汉大学学报·信息科学版, 2004, 29(12):1101-1105) |
| [12] | Zhao Shuangming,Guo Qiuyan,Luo Yan, et al. Quaternion-based 3D Similarity Transformation Algorithm[J]. Geomatics and Information Science of Wuhan University, 2009, 34(10):1214-1217(赵双明,郭秋燕,罗研,等. 基于四元数的三维空间相似变换解算[J]. 武汉大学学报·信息科学版, 2009, 34(10):1214-1217) |
| [13] | Yao Yibin, Huang Chengmeng, Li Chengchun, et al. A New Algorithm for Solution of Transformation Parameters of Big Rotation Angle's 3D Coordinate[J]. Geomatics and Information Science of Wuhan University, 2012, 37(3):253-256(姚宜赋, 黄承猛, 李程春, 等. 一种适合于大角度的三维坐标变换参数求解算法[J]. 武汉大学学报·信息科学版, 2012, 37(3):253-256) |
| [14] | Zeng Huai'en, Huang Shengxiang. A Kind of Direct Search Method Adapted to Solution of 3D Coordinate Transformation Parameters[J]. Geomatics and Information Science of Wuhan University, 2008, 33(11):1118-1121(曾怀恩, 黄声享. 三维坐标转换参数求解的一种直接搜索法[J]. 武汉大学学报·信息科学版, 2008, 33(11):1118-1121) |
| [15] | Li Yaping, Huang Chongchao. Using Real Quaternions to Represent Rotation in Three Dimensions[J]. J. Wuhan Univ. of Hydr. & Elec. Eng., 1995, 28(6):607-612(李亚萍, 黄崇超. 实四元数与三维旋转[J]. 武汉水利电力大学学报, 1995, 28(6):607-612) |
| [16] | Shuster M D, Oh S D. Three-axis Attitude Determination from Vector Observations[J]. Journal of Guidance and Control, 1980, 4(1):70-77 |
| [17] | Zhou Shaolei, Cong Yuancai, Li Juan, et al. Comparison of Algorithms for Extracting Quaternion from DCM[J]. Journal of Chinese Inertial Technology, 2008, 16(4):415-418(周绍磊, 丛源材, 李娟, 等. 方向余弦矩阵中四元数提取算法比较[J]. 中国惯导技术学报, 2008, 16(4):415-418) |
| [18] | Bar-Itzhack I Y. New Method for Extracting the Quaternion from a Rotation Matrix[J]. Journal of Guidance and Control, 2000, 23(6):1085-1087 |
| [19] | Sheng Zhou, Xie Shiqian, Pan Chengyi. Probability Theory and Mathematical Statistics[M]. Beijing:Higher Education Press, 1989:375-376(盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京:高等教育出版社, 1989:375-376) |
| [20] | Zhang Haolin, Lin Jiarui, Zhu Jigui. Three-dimensional Coordinate Transformation Accuracy and Its Influencing Factors[J]. Opto-Electronic Engineering, 2012, 39(10):26-31(张皓琳, 林嘉睿, 邾继贵. 三维坐标转换精度及其影响因素的研究[J]. 光电工程, 2012, 39(10):26-31) |
 2016, Vol. 41
2016, Vol. 41


