
文章信息
- 丁士俊, 何亮云, 李鹏鹏
- DING Shijun, HE Liangyun, LI Pengpeng
- 斜轴墨卡托圆柱投影及其在高速铁路控制网中的应用
- Oblique Mercator Projection and Its Application to Control Network for High Speed Railway
- 武汉大学学报·信息科学版, 2016, 41(4): 541-546
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 541-546
- http://dx.doi.org/10.13203/j.whugis20130120
-
文章历史
- 收稿日期: 2015-10-10

2. 国家测绘局精密工程测量与工业测量重点实验室, 湖北 武汉, 430079;
3. 湖南城市学院, 湖南 益阳, 413000;
4. 武汉市测绘研究院, 湖北 武汉, 430022
2. Key Laboratory of Precise Engineering and Industry Surveying, State Bureau of Surveying and Mapping, Wuhan 430079, China;
3. Hunan City University, Yiyang 413000, China;
4. Wuhan Geomatic Institute, Wuhan 430022, China
高速铁路建设对其基础及轨道的施工要求精度很高,根据我国《客运专线无砟轨道铁路工程测量技术暂行规定》,施工控制网平面坐标系采用工程独立坐标系,其坐标系的设计满足如下要求:边长投影面为线路设计的高程面(轨道平均高程面),且边长投影长度的变形小于10 mm/km。采用分带投影,在不考虑高程对长度变形影响的情况下,分带边缘子午线距中央子线不得超过29 km,分带东西跨度为58 km。对于东西跨度较长的高铁线路,为了控制边长的投影变形,需要划分较多投影带,建立众多的独立坐标系,容易给整条铁路施工带来不便。如果以铁路中心线为中央子午线,使得圆柱面与铁路中心线相切,采用斜轴墨卡托圆柱投影,可以有效控制长度投影变形以及分带过多的问题。文献[1]提出了蛇形投影方法来解决长线路铁路投影的变形问题。文献[2]通过地面点对球面进行拟合来实现椭球面向球面的过渡,必须将椭球面元素(如大地经纬度)投影到球面上,然后进行斜轴墨卡托圆柱投影,但在一定的范围内地面点的选择具有一定的随意性,如果选择不同的拟合点,会导致拟合的球面以及斜轴墨卡托投影平面直角坐标存在一定的差异,这样会给GPS控制网的检测(或复测)带来不便。文献[3, 4]利用地图投影理论将椭球面投影到球面,然后通过球面极坐标系过渡,实现斜轴墨卡托圆柱投影,较好地控制了投影长度变形问题,但没有顾及高程对长度变形的影响。文献[5, 6]给出了斜轴墨卡托投影的正反算公式,是一种比较好的算法,但计算较为复杂。本文针对上述问题,从控制长度变形的角度,研究了长线路铁路GPS控制网斜轴墨卡托圆柱投影的基本理论与方法。算例分析表明,斜轴墨卡托圆柱投影与高斯投影比较,在高速铁路及其线路工程的应用中具有一定的优越性。
1 投影与高斯投影长度变形地图投影是将椭球面的元素如坐标、方位角和距离按一定的数学法则投影到平面上,其投影面是可以展开成为平面的曲面,如椭圆柱面、圆柱面或平面等。投影的种类与方法很多,按照投影面与原面的相对位置关系来分可分为正轴投影、横轴投影与斜轴投影。无论何种投影,在投影的应用过程中都会产生变形。高斯-克吕格投影是横轴椭圆柱等角投影,其长度变形包括高程归化改正与投影改正。
高程归化改正是将地面上观测的长度归算到参考椭球面上而产生的改正[7]:
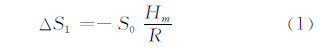
式中,S0是地面观测长度;Hm是地面两点高出参考椭球面的平均高度;R是归算边方向参考椭球法截弧的曲率半径(一般取地球的长半径R=6 370 km)。按式(1)计算,地面点高出椭球面65 m,则高程归化改化对每km长度变形量(或长度变形系数)为10 ppm。
投影改正是将参考椭球面上的长度投影到高斯平面上而产生的改正[7]:
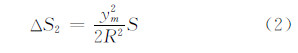
式中,ym是高斯平面上边长两端点横坐标的平均值;S为参考椭球面长度。表 1表示每km长度改正与中央子午线的距离ym的关系。
| ym/km | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| ΔS2/mm | 0.0 | 0.3 | 1.2 | 2.8 | 4.9 | 7.7 | 11.1 | 15.1 | 19.7 | 25.0 |
由表 1可知,椭球面长度投影到高斯平面上,距中央子午线越远,变形越大,如果不考虑高程归化改正对长度变形的影响,投影距中央子午线29 km的范围内其变形不超过10 ppm(1/10万),45 km范围内其变形小于25 ppm(1/4万)。
考虑到上述两个长度变形因素,则每km总的长度变形量为:
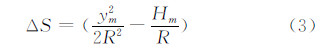
减少长度变形的方法通常是选择中央子午线与边长投影面,使得每km总的长度变形最大值在规范所要求的范围内:
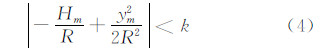
式中,k为每km长度变形系数。
在工程实践中,边长投影面一般取测区的平均高程面(或设计高程面)。假设测区控制网的平均高程面的高程为Hm,控制网一边长的平均高程为Hs,ΔH=Hs-Hm,由式(4)可得到中央子午线一侧的有效的变形区间计算公式:
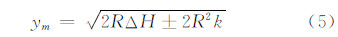
从表 2可以看出,高程归化改正随高差变化,有效的变形区间也将随之变化,当边长高程面高出平均高程面60 m时,有效的变形区间为39 km,边长高程面低于平均高程面60 m,有效的变形区间为7 km;有效的变形区间离开中央子午线后,会随高差的增大而越来越小,若工程控制网在有效变形区间之外,则长度变形不能满足要求,因此高速铁路坐标系带宽的选择可参照表 2和表 3来加以确定。总体而言,影响坐标系选择的因素主要包括高速铁路的走向、地理位置以及线路纵断面的平均高度(一般而言,控制网点的相对高差较小,对于高程归化改正的影响可以忽略不计)。就长度变形小于1/10万的高速铁路而言,对于南北走向的铁路,其跨越的经度范围较小,可根据铁路的位置是否落在有效的变形区域内,考虑按国家坐标系分带或者任意带坐标系来分带;对于东西走向的铁路,跨越的经度范围较大,45″或30″分带为首选分带方法,但分带的带数较多,在此情况下,考虑斜轴投影能较好地解决分带较多的问题。
| ΔH/m | 0 | ±30 | ±40 | ±50 | ±60 | ±70 | ±80 | ±100 |
有效变形区间ym /km(高于) 有效变形区间ym /km(低于) | 0~29 0~29 | 0~34 0~21 | 0~36 0~17 | 0~38 0~13 | 0~39 0~7 | 9~42 ~ | 14~43 ~ | 22~46 ~ |
| 有效变形区间大小/km | 29 29 | 34 21 | 36 17 | 38 13 | 39 8 | 33 ~ | 29 ~ | 24 ~ |
| 纬度 | 3°带 | 1.5°带 | 1°带 | 45″带 | 30″带 |
| 25° | 151 | 76 | 50 | 38 | 25 |
| 30° | 145 | 73 | 48 | 36 | 24 |
| 35° | 137 | 67 | 45 | 34 | 23 |
| 40° | 128 | 64 | 42 | 32 | 21 |
| 45° | 118 | 59 | 39 | 30 | 20 |
就线路控制网而言,采用斜轴墨卡托圆柱投影,使圆柱面与线路中心线相切进行投影,线路中心线投影长度不变,离开线路中心线的点会发生变形。由于采用椭球作为原面计算多有不便,斜轴墨卡托投影通常采用球面作为投影原面,因此需要将椭球面元素投影到球面上。另外,通常取线路的平均高程面作为线路的设计高程,为了控制高程归化改正对长度变形的影响,一般取平均高程面作为边长改化的高程面,因此建立工程坐标系时还要考虑椭球的变换问题。
2.1 独立椭球的确定依照工程独立坐标系的确定方法,通常选择线路工程设计高程面,将控制网边长观测量归算到该高程面上,与该高程面相对应的椭球称之为工程椭球(或区域性椭球),统称为独立椭球[7, 8, 9]。独立椭球的确定依赖于国家坐标系所对应的参考椭球,按照一定的准则进行椭球变换得到。椭球变换方法有椭球膨胀法、椭球变形法及椭球平移法等,本文选择椭球变形法作为独立椭球的确定方法。
依照椭球变形法的基本原理,独立坐标系所对应的椭球参数相应的计算公式为[7, 9]:

式中,B0为测区中心点(或基准点)的纬度;N0= ;Hm为测区平均高程面高程;a,e分别为参考椭球的长半径与第一偏心率。
;Hm为测区平均高程面高程;a,e分别为参考椭球的长半径与第一偏心率。
经椭球变换后,独立椭球下控制点大地坐标分别为(B′i,L′i,H′i),B′i=Bi+ΔBi,L′i=Li+ΔLi,H′i=Hi+ΔHi,大地坐标的变换量ΔBi、ΔLi、ΔHi计算公式如下[7, 9]:

式中,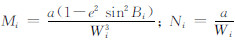 ;Wi=
;Wi=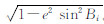 。
。
在斜轴投影中,直接采用椭球大地坐标推求投影平面直角坐标比较复杂。为了斜轴投影计算方便,先将椭球面的大地坐标等角投影到球面上,球半径取测区某中心点纬度(标准纬度)B′0处的平均曲率半径,由地图投影基本理论可知,将独立椭球大地坐标(B′,L′)投影至球面大地坐标(φ,λ),其球面投影计算公式如下[10]:
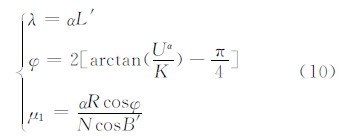
式中,μ1是长度变形系数;其他各系数分别为:

式中,R为独立椭球在B′0处的平均曲率半径;M0、N0分别为独立椭球在B′0处子午线与卯酉线的曲率半径;e独为独立椭球的第一偏心率。
椭球面在球面的局部描写长度变形系数μ1与纬度有关。由表 4可知,中心点纬度处,其纬线(又称为标准纬线)长度变形为零,点距标准纬线越远,其长度变形越大,但其长度变形数值相对较小,即使纬差相差3°,其长度变形小于0.3 ppm,因此可以忽略不计。
| 纬度 | 27° | 28° | 30° | 32° | 33° |
| μ1 | 0.27 | 0.08 | 0.00 | -0.08 | 0.28 |
要确定斜轴球面大地坐标,斜轴圆球中央子午线取线路中心线的走向,在线路中心线上选择一点A作一垂直于中心线AB的大圆作为斜轴圆球的赤道,将斜轴圆柱投影转换为横轴圆柱投影,即斜轴圆球的大地坐标可由球面的大地坐标通过球面极坐标过渡来实现,球面极坐标的建立如图 1所示。

|
| 图 1 球面极坐标 Fig. 1 Sphere Polar Coordinate |
在球面上以线路中心线一点A为极点建立球面极坐标系,计算线路各点的极坐标。假设点A与点i的球面大地坐标分别为(φA,λA),(φi,λi),以点A为极点,点i的极坐标(αi,σi)可由球面三角形公式计算[11]:
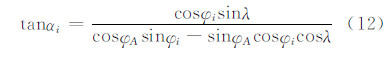
式中,λ=λi-λA;0≤αi<2π。计算时需要对αi进行象限判断。
令p=cosφisinλ,q=cosφ0sinφi-sinφ0cosφicosλ,
则有:
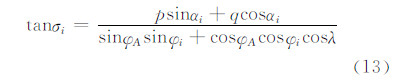
式中,0<σi≤π,并对σi进行象限判断。
在球面上,若线路中心线AB在以A点为极点的极坐标中的方位角为αB,以线路的中心线为斜轴参考圆球投影的中央子午线,则参考圆球上各点在斜轴参考圆球上以A为极点的极坐标为:
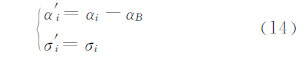
根据球面三角公式,由球面大地主题正算计算公式可得斜轴球面点的新的大地坐标(φ′,λ′)[11]。
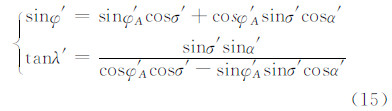
式中,λ′=λ′i-λ′A。当φ′A=0,λ′A=0时,式(15)可简写为:
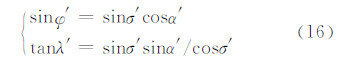
通过上述计算,得到斜轴参考球面上各点大地坐标(φ′,λ′),按照等角横轴圆柱投影,计算其平面坐标(x,y),由于x是λ′的偶函数,y是λ′的奇函数,可得到如下方程:
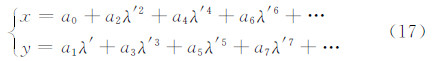
式中各系数分别为[2]:
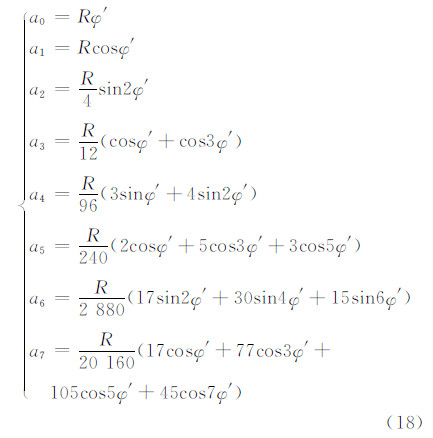
如果按照等角正轴圆柱投影,使得线路中心线与斜轴圆球的赤道重合,则斜轴圆球各点以点A为极点的极坐标为:
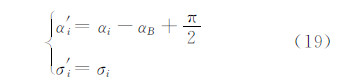
按式(15)计算斜轴圆球上各点的经纬度(φ′,λ′),则斜轴墨卡托投影的平面坐标为[12]:
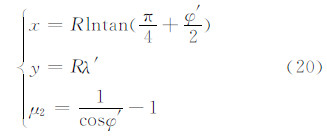
式中,R为独立椭球在B′0处的平均曲率半径;μ2为正轴圆柱投影长度变形系数。
3 算例分析某段高速铁路CPI级GPS控制网数据取自文献[3]。该线路控制网走向为东西方向,东西范围跨度约为190 km,位于东经109°38″~121°20″,北纬31°09′~32°02′,已知该线路工程GPS控制点WGS84空间直角坐标与大地坐标见表 5(由于篇幅限制,仅取部分控制点)。如果按照高斯投影处理,由表 1与表 3可知,满足每km长度变形小于10 ppm,该段控制网至少要划分4个投影带才能满足要求。采用斜轴投影计算可以不用分带,具体计算如下。
| 点号 | X/m | Y/m | Z/m | B(° ″ ′) | L(° ″ ′) | H/m | |
| CPI127 | -2 677 542.556 5 | 4 703 688.941 8 | 3 363 142.3014 | 32 01 43.4025 | 119 39 01.4323 | 19.3411 | |
| CPI128 | -2 680 330.960 2 | 4 703 349.318 7 | 3 361 397.489 4 | 32 00 36.6993 | 119 40 40.1665 | 14.0886 | |
| CPI133 | -2 697 814.366 2 | 4 700 586.726 1 | 3 351 322.504 8 | 31 54 11.2414 | 119 51 10.3242 | 11.1680 | |
| CPI141 | -2 726 104.822 4 | 4 691 704.582 7 | 3 340 926.483 7 | 31 47 33.9345 | 120 09 31.0935 | 9.5878 | |
| CPI145 | -2 739 356.063 2 | 4 689 886.243 8 | 3 332 689.098 4 | 31 42 19.3972 | 120 17 20.9093 | 11.2790 | |
| CPI151 | -2 759 302.854 9 | 4 687 238.685 8 | 3 320 021.783 6 | 31 34 16.3056 | 120 29 04.7224 | 12.3903 | |
| CPI157 | -2 777 655.313 3 | 4 686 756.535 9 | 3 305 460.767 2 | 31 25 01.9062 | 120 39 12.7657 | 10.2897 | |
| CPI160 | -2 788 561.747 2 | 4 683 268.729 6 | 3 301 251.518 7 | 31 22 21.7509 | 120 46 15.1145 | 12.6418 | |
| CPI168 | -2 815 973.960 4 | 4 669 263.626 7 | 3 297 841.822 2 | 31 20 12.1144 | 121 05 37.1339 | 12.4068 | |
| CPI175 | -2 835 947.098 3 | 4 664 052.460 2 | 3 288 154.199 1 | 31 14 04.0193 | 121 18 05.1257 | 13.6984 | |
| CPI176 | -2 837 729.696 9 | 4 664 642.199 2 | 3 285 794.739 9 | 31 12 34.4341 | 121 18 51.0911 | 13.6892 | |
| CPI178 | -2 840 296.108 3 | 4 666 457.278 6 | 3 281 028.832 4 | 31 09 33.5484 | 121 93 82.5816 | 13.7706 |
1)以测区的平均高程(平均高程12 m)作椭球变换,利用式(6)~(9)进行椭球变换计算。
2)通过椭球变换得到工程独立椭球,以测区中心点纬度32°作为标准纬度,实现椭球面向球面投影,采用式(10)、(11)进行计算。
3)以CPI127~CPI178作为线路中心线走向,进行斜轴墨卡托投影,计算结果见表 6。由表 6可知,该网平均高程约为12 m,控制点相对于平均高程高差较小,边长高程归化改正长度变形系数ΔS1小于2 ppm;椭球面投影到球面长度变形系数μ1可以忽略不计。由于该网控制点至中心线的最大距离约为9 km(控制点CPI157的y坐标),球面投影到平面的长度变形系数μ2的最大值为1.02 ppm,总体长度变形系数Σ小于2 ppm,完全满足每km长度变形10 ppm(1/10万)的精度要求。
| 点号 | X/m | y/m | ΔS1 /ppm | μ1 /ppm | μ2/ppm | Σ/ppm |
| CPI127 | 0.000 0 | 0.000 0 | -1.15 | 0.00 | 0.00 | -1.15 |
| CPI128 | 3 277.411 8 | 439.813 9 | -0.33 | 0.00 | 0.00 | -0.33 |
| CPI133 | 23 571.761 4 | 2 156.314 7 | 0.13 | 0.00 | 0.06 | 0.19 |
| CPI141 | 54 685.389 1 | -2 232.801 8 | 0.38 | 0.00 | 0.06 | 0.44 |
| CPI145 | 70 276.363 4 | -314.982 2 | 0.11 | 0.00 | 0.00 | 0.11 |
| CPI151 | 93 845.109 6 | 2 825.057 4 | -0.06 | 0.00 | 0.10 | 0.04 |
| CPI157 | 116 421.684 4 | 9 099.443 5 | 0.27 | 0.00 | 1.02 | 1.29 |
| CPI160 | 128 517.791 1 | 7 512.815 3 | -0.10 | 0.00 | 0.70 | 0.60 |
| CPI168 | 156 804.749 5 | -5 098.625 2 | -0.06 | 0.00 | 0.32 | 0.26 |
| CPI175 | 179 596.036 0 | -5 799.026 7 | -0.27 | 0.00 | 0.41 | 0.15 |
| CPI176 | 182 078.870 9 | -4 087.878 2 | -0.27 | 0.01 | 0.21 | -0.05 |
| CPI178 | 186 064.356 6 | 0.000 0 | -0.28 | 0.01 | 0.00 | -0.27 |
从上述算例可得出如下结论:在高铁或精度要求较高的线路工程控制网中,对于东西走向的线路,从控制长度变形减少分带的角度而言,斜轴墨卡托投影与高斯投影比较而言具有一定的优越性。GPS控制网图上设计时,控制点点位设计(控制点距线路中心线的距离与点位高程)要从满足长度变形的要求上加以考虑,可按式(3)进行长度变形估算,使其满足长度变形的设计要求。如果线路相对较长,线路高程变化较大或者线路方向发生变化,在顾及控制点距线路中心线的距离等因素的情况下,可以考虑分段(分带)进行斜轴投影。
| [1] | Ⅱiffe J C, Arthur J V. The Snake Projection:A Customized Grid for Rail Projections[J]. Survey Review, 2007, 39:90-99 |
| [2] | Wang Peng. Reseach on Data Processing Methods of GPS Engineering Control Network and Soft Development[D]. Chengdu:Southwest Jiaotong University, 2008(王鹏. GPS工程控制网数据处理方法的研究及软件研制[D]. 成都:西南交通大学, 2008) |
| [3] | Feng Guangdong, Wang Peng. Discussion on Projection Distortion Methods of GPS Control Network on High Speed Railway[J]. Railway Investigation and Surveying, 2011, 1:4-7(冯光东,王鹏.高速铁路GPS控制网投影变形处理方法的探讨[J].铁路勘测,2011, 1:4-7) |
| [4] | Liu Lingjie, Yuan Yulei, Wei Jiandong. Analysis of Oblique Mercator Projection Application in High Speed Railway Surveying[J]. Bulletin of Surveying and Mapping, 2009, 2:43-45(刘灵杰, 原玉磊, 卫建东. 斜轴墨卡托投影在高速铁路测量中的应用分析[J]. 测绘通报,2009, 2:43-45) |
| [5] | Wang Jiexian, Wu Jicang, Gao Xiaobing. Oblique Mercator Projection and Its Application on High Speed Railway Construction[J]. Geotechnical Investigation & Surveying, 2011, 8:69-72(王解先, 伍吉仓, 高小兵. 斜轴墨卡托投影及其在高铁建设工程中的应用[J]. 工程勘察, 2011, 8:69-72) |
| [6] | Snyder J P. Map Projections:A Working Manual[OL]. http://pubs.er.usgs.gov/publication/pp1395, 1987 |
| [7] | Shi Yimin. Modern Geodetic Control Survey[M].Beijing:Surveying and Mapping Press,2008(施一民.现代大地控制测量[M].北京:测绘出版社,2008) |
| [8] | Li Shian, Liu Jingnan, Shi Chuang.Study of the Ellipsoid Transformation Coordinate System Using GPS Technique[J].Geomatics and Information Science of Wuhan University, 2005,30(10):889-891(李世安,刘经南,施闯.应用GPS建立区域独立坐标中椭球变换的研究[J].武汉大学学报·信息科学版,2005,30(10):889-891) |
| [9] | Ding Shijun, Chang Kaishi,Gao Suoyi. Research of Local Independent Ellipsoid Transformation and Coordinates Transformation[J]. Bulletin of Surveying and Mapping, 2008, 8:4-6(丁士俊, 畅开蛳, 高锁义. 独立网椭球变换与坐标转换的研究[J]. 测绘通报, 2008, 8:4-6) |
| [10] | Sun Da, Pu Yingxia. Map Projections[M]. Nanjing:Nanjing University Press, 2012(孙达, 蒲英霞. 地图投影[M]. 南京:南京大学出版社, 2012) |
| [11] | Kong Xiangyuan, Guo Jiming, Liu Zongquan. Fundation of Geodesy[M].Wuhan:Wuhan University Press, 2010(孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 武汉:武汉大学出版社, 2010) |
| [12] | Li Guocao, Yang Qihe, Hu Dingquan. Map Projections[M]. Beijing:The People's Liberation Army Press, 1993(李国藻, 杨启和, 胡定荃. 地图投影[M]. 北京:解放军出版社, 1993) |
 2016, Vol. 41
2016, Vol. 41



