文章信息
- 张鑫, 陈华明, 黄仰博, 张国柱, 欧钢
- ZHANG Xin, CHEN Huaming, HUANG Yangbo, ZHANG Guozhu, OU Gang
- 利用旋转天线载波相位双差进行欺骗干扰检测技术
- Spoofing Detection Technique Based on Carrier Phase Double Difference of Spin-Antenna
- 武汉大学学报·信息科学版, 2016, 41(4): 529-534
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 529-534
- http://dx.doi.org/10.13203/j.whugis20140360
-
文章历史
- 收稿日期: 2014-10-09

2. 海军装备研究院航空装备论证研究所, 上海, 200436
2. Aviation Equipment Institute, Naval Armament Academe, Shanghai 200436, China
欺骗干扰是通过转发或自主产生与真实信号非常类似的欺骗信号,阻塞目标导航系统或使其得出错误定时定位结果的干扰方式,已逐渐成为卫星导航系统的重要威胁[1]。目前常用的欺骗干扰都是以单一天线发射多路欺骗信号构成的,因此国内外对欺骗干扰检测技术的研究也主要针对这一特点[1, 2, 3]。在这些研究中,利用单天线运动进行欺骗干扰检测是一种重要方法。该方法由Nielsen和Broumandan提出,利用单天线接收机运动时不同历元时刻相关器输出来进行欺骗干扰检测,其原理是基于欺骗信号间空间相关性明显强于真实信号[4, 5, 6]的特点。然而,这种方法需要对所有的真实与欺骗信号同时进行捕获跟踪处理,并将相关器输出结果进行两两组合检测,计算复杂度高,需要对接收机算法进行大量修改。同时,为了保证算法的有效性,还要求天线运动具有一定的随机性和尺度。通常安装位置固定和精确已知的授时型接收机或差分基站接收机是无法满足这种要求的。因此这类接收机的欺骗干扰检测仍需要依靠传统的天线阵技术[7]。
然而,由文献[8]的分析可知,接收机天线运动时,接收机位置变化导致了与信号发射源间的距离变化,而不同信号距离变化中包含了入射信号的到达角信息。基于此,本文提出了一种基于旋转天线载波相位双差的卫星导航接收机欺骗干扰检测技术,在无须修改接收机信号处理算法的条件下,通过对天线匀速旋转条件下接收机输出载波相位测量值的处理,实现了欺骗干扰信号的到达角检测,并对影响检测性能的因素和提升检测性能的方法进行了分析。该技术中接收机天线虽然处于运动状态,但其运动轨迹绕圆心不变。若将已知固定站点的精确点位作为接收机天线旋转圆心,则可将该技术用于对各类固定站点接收机进行抗欺骗干扰改装。
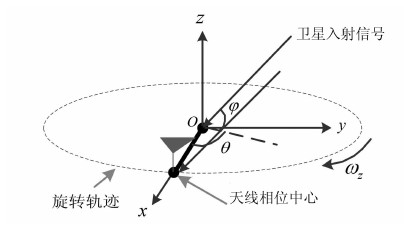
1 旋转天线输出载波相位以接收机天线相位中心旋转圆周的圆心为坐标系原点O,建立直角坐标系(x,y,z),Ox轴的指向为0时刻原点O到天线相位中心,如图 1所示。
|
| 图 1 旋转天线模型 Fig. 1 Spin-Antenna Model |
由于原点O位置固定且在地心地固(Earth-Centered Earth-Fixed,ECEF)坐标系中的位置精确已知(可达mm量级[9]),接收机天线相位中心绕原点O以角速度ωz做匀速圆周运动,圆周半径为r。旋转过程中得到某颗卫星的N个历元时刻载波相位测量值为:
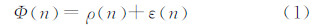
式中,n=0,1,2,…,N-1;ρ(n)为载波相位真值;ε(n)为载波相位测量噪声,可看作零均值高斯白噪声。由文献[8]可知,ρ(n)可以分解为:
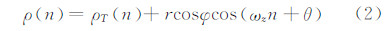
式中,ρT(n)为静止原点O的载波相位真值;φ和θ分别是信号相对天线旋转平面的俯仰角和方位角。
在较短的测量时间间隔内,无论真实或欺骗信号的ρT(n)的变化可认为完全由卫星的运动产生,否则接收机将可以通过定位解的检验来检测欺骗干扰[10]。
将式(2)代入式(1)可得:
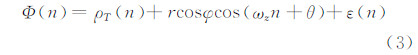
由式(3)可见,载波相位测量值序列中包含了入射信号俯仰角φ和方位角θ的信息。
2 欺骗干扰到达角检测原理令Φ=[Φ(0)Φ(1)Φ(2)… Φ(N-1)]T,由于Φ序列为包含有整周模糊的非确定值,因此无法直接从Φ序列得到φ和θ的信息,从而进行到达角检测。对Φ进行前向后向差分运算,可得如下差分序列:
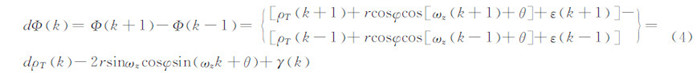
式中,k=1,2,3,…,N-2;γ(k)为噪声项差分运算得到的新噪声项。
对已经精确标定了O点位置的接收机,在较短的时间内,式(4)中的dρT(k)项为两个历元间卫星相对O点的距离变化,称之为平动项[11]。由星历数据对卫星轨道的计算,可以将式(4)中的平动项dρT(k)消除,得到只包含天线旋转产生的载波相位测量值变化和噪声项的差分序列,并将该序列表示为矢量形式:
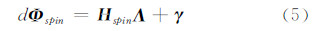
式中,

易证,当限制φ∈[0,π/2]和θ∈[0,2π]时,不同的φ和θ将产生不同的Λ。
对于真实卫星信号,不同卫星信号到达天线旋转平面的φ和θ不可能完全一致。而对于由单一天线发射的不同路欺骗干扰信号,信号的到达角完全相同。根据这一特点,对两路信号i和j的载波相位差分序列进行双差,可得到以下双差序列:
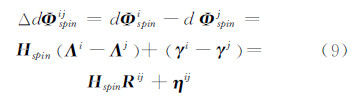
当两路信号为真实卫星信号时Rij可认为不为0,而当两路信号为欺骗信号时,Rij等于0,据此可对欺骗干扰进行检测。
3 基于非相关差分的检测方法根据文中分析的基于旋转天线的欺骗干扰到达角检测原理,可得如下二元假设检验模型:
H1:参与载波相位双差检测的两路信号均为欺骗干扰信号;
H0:参与载波相位双差检测的两路信号至少一路为真实卫星信号。
分析式(9)中的噪声分布特性可知,虽然由于ε(n)可看作零均值高斯白噪声,在经过不同历元的差分运算后,γ(k)不再是白噪声,但仍为高斯噪声。相应地,ηij=γi-γj也为高斯色噪声,因此无法对式(9)使用经典线性模型的广义似然比判决(generalized likelihood ratio test,GLRT)。
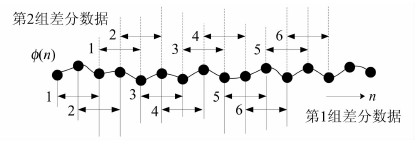
如果将差分序列Φ分为两组,每组差分序列的差分对中不包含相同的观测点,这种差分方式得到的两组序列中的噪声均为高斯白噪声,如图 2所示。
|
| 图 2 非相关差分方法 Fig. 2 Non-related Difference Method |
一路信号的第1组非相关差分序列dΦspin,1可以表示为:
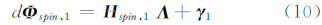
令h=0,1,2…,hmax,hmax=floor[(N-4)/4],则
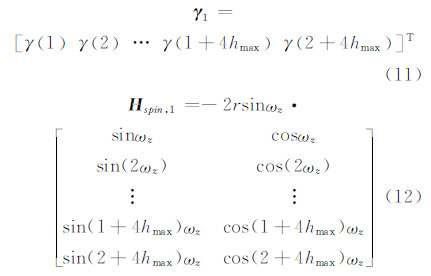
此时两路信号i和j的载波相位差分序列双差后的序列为:
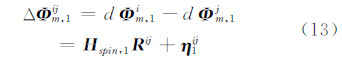
式中,噪声η1ij的分布为高斯白噪声。
非相关差分得到的式(13)满足经典线性模型的GLRT条件,但H1和H0对应的数学模型变为:
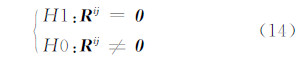
易证,这种情况下仍可采用经典线性模型的GLRT方法,但检验统计量判决H1成立的条件由大于门限改为小于门限,即有:
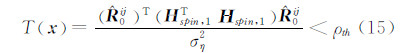
则判H1成立,其中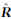 0ij为在H0条件下的极大似然估计(maximum likehood estimate,MLE)量,ρth为检测门限,ση2为噪声方差,并且有:
0ij为在H0条件下的极大似然估计(maximum likehood estimate,MLE)量,ρth为检测门限,ση2为噪声方差,并且有:
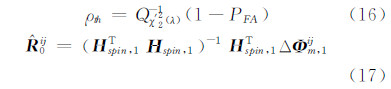
式中,PFA为虚警率;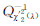 (&buuL;)为自由度为2、非中心参数为λ的非中心χ2分布右尾概率的反函数。
(&buuL;)为自由度为2、非中心参数为λ的非中心χ2分布右尾概率的反函数。
由经典线性模型的GLRT检测器检测量分布特性可知,利用式(15)给出的检测量,检测器的检测概率为:
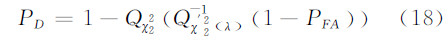
式中,PD为检测概率;PFA为虚警概率;Qχ22(&buuL;)表示自由度为2的中心χ2分布右尾概率;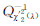 (&buuL;)为自由度为2、非中心参数为λ的非中心χ2分布右尾概率的反函数,其中非中心化参数λ可以表示为:
(&buuL;)为自由度为2、非中心参数为λ的非中心χ2分布右尾概率的反函数,其中非中心化参数λ可以表示为:
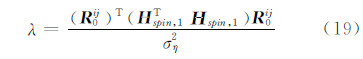
式中,R0ij为H0假设下的真值,只与两路信号的入射角度有关;Hspin,1则为线性模型的观测矩阵,与旋转角速度ωz、旋转臂长r和数据长度N有关;σ2η与接收机的载波相位测量精度有关,接收机确定后可认为保持不变。
由于ωz、r和N都可以事先选择确定,因此Hspin,1在计算λ时为已知量。对于两路信号的入射角度,虽然是确定值,但通常都是未知的。因此Rij0的确定需要先对两路信号的到达角进行估计。相应的估计方法是利用一段时间内信号入射到达角变化缓慢的特点,由载波相位测量值的非相关差分序列进行MLE得到。
由Rij0的估计值和事先确定的Hspin,1,就可以由式(19)计算得到非中心化参数λ,进而得到指定虚警概率下的检测概率。
4.2 检测性能提升对于入射方向确定的信号,使用长度为N的数据进行欺骗干扰检测,当N较大时,令Rij0=[p q]T,且ωz满足0<ωz<π时[12],则近似有:
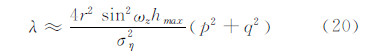
可见,r或sin2ωz增大,都会导致λ增大,从而使得一定虚警率PFA下的检测门限更大,相应提升了检测概率。然而增加旋转臂长r或改变sin2ωz都可能导致其他问题,如较大的旋转臂会占用大的空间,不利于实际旋转天线的安装和运行,而提高旋转频率则需要对接收机算法进行适应性修改,否则会影响载波相位测量值的精度等等。
式(20)中,hmax增大也会使λ增大,相应使检测门限增大,提高检测概率。而hmax增加只需要增大构成检测量的数据长度N。
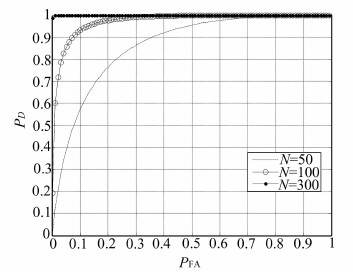
令接收机输出载波相位测量值的测量精度σε=0.01ζ,ζ为载波波长。图 3为不同数据长度下,旋转臂长r为0.5ζ,转速ωz为0.05π,两路真实信号方位角/俯仰角分别为(155°,50°)和(160°,55°)时的欺骗信号检测ROC曲线。
|
| 图 3 不同数据长度下欺骗干扰检测ROC Fig. 3 Spoofing Detection ROC at Different Data Length |
可见,当参与判决的数据长度由50增加到300时,所设定两路信号在虚警率为0.01时对应的检测概率由0.114 3提升到0.998 9。虽然增加数据长度导致单次判决时间由5 s增加到30 s,但在这段时间内两路信号相对于固定站点的角度变化可以忽略,不会对检测结果产生影响。
可见,增大数据长度N是提升旋转天线欺骗干扰检测性能的必然选择。
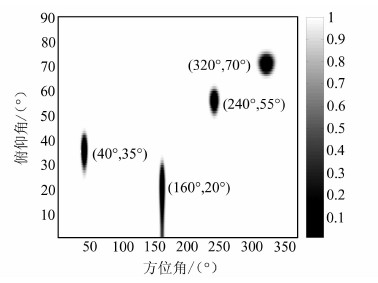
4.3 检测盲区定义由于式(8)的取值与到达角间的复杂关系,式(20)中的p和q与到达角之间的关系也难以直观表达。取两路信号中一路为参考信号,在整个方位角/俯仰角范围内,按照一定的角度分辨率遍历计算另一路信号从不同角度入射时在给定虚警率下的检测概率分布,可说明两信号到达角差异对检测性能的影响。设4组参考信号方位角/俯仰角分别为(40°,35°)、(160°,20°)、(240°,55°)和(320°,70°),角度分辨率设为1°,虚警率设为0.01,旋转臂长r为0.5ζ,转速ωz为0.05π,数据长度N为200,可得如图 4所示各信号的检测概率分布。
|
| 图 4 不同参考信号到达角下的检测概率分布 Fig. 4 Detection Probability Distribution Under Different Reference Signal Incident Angle |
由以上遍历分析方法可见,当两路真实信号到达角差异较小时,欺骗干扰检测性能急剧下降。特别是当两路真实信号是从同一方向入射时,会有λ=0的情况出现,此时H0与H1条件下的检测量分布完全相同,检测概率等于虚警概率。此时,已不可能由信号的到达角特性来区分欺骗与真实信号。
并且,由图 4中各参考信号的检测概率分布可知,不同入射角度参考信号检测概率较小的区域都集中在该参考信号入射角周边。设定一个检测概率的门限,参考信号周边小于该检测概率门限的区域定义为检测盲区,检测盲区的大小可由分辨率格数表示。表 1为虚警率0.01,检测概率门限为0.99,N分别为150、200时各参考信号的检测盲区大小。由表 1可知,检测盲区的定义,可用于比较不同条件下的全局检测性能。
| 信号1 | 信号2 | 信号3 | 信号4 | |
| N=150 | 278 | 389 | 266 | 398 |
| N=200 | 201 | 318 | 194 | 296 |
对于落入参考信号检测盲区中的信号,可以采取两种措施进行处理。第一种是直接判H1成立,即两信号为欺骗信号。第二种则是将检测门限调整为由检测概率门限求解得到的检测门限。易知,无论经过哪种处理,检测盲区中的实际虚警率均不再为恒定的设定值,而是迅速提高。然而在实际星座中,两颗真实卫星位置很近的情况极少出现,即便出现也可先作为欺骗信号排除,待排除了所有欺骗干扰信号,并由真实信号解算得到天线阵的位置和姿态后,进一步通过星历数据恢复被错误排除的真实信号。因此,这种检测盲区内虚警率的增加,避免了由于检测性能降低而导致接收机将欺骗信号作为真实信号使用时的严重影响,也不会给接收机最终的性能带来损失。
5 仿真分析以全球定位系统L1C/A信号为例,对所提出的旋转天线载波相位双差欺骗干扰检测方法进行仿真分析,仿真验证条件如下。
1)设置两路真实L1C/A信号入射到达旋转天线平面,并且以旋转圆心为原点、天线阵平面为水平面,0时刻相对天线旋转臂的方位/俯仰角分别为(148°,50°),(158°,53°);
2)设置两路L1C/A欺骗干扰信号从同一入射角到达旋转天线平面,其方位/俯仰角为(160°,55°);
3)对所设置的所有4路信号进行1~4的统一编号,其中第1~2路表示欺骗干扰信号,第3~4路表示真实卫星信号;
4)接收机对各路信号的载波相位测量精度相同,均为0.01周;
5)设置虚警概率PFA为0.01,旋转臂长r为0.5ζ,数据长度N为150。接收机载波相位输出频率fo为10 Hz,天线旋转频率fz为0.25 Hz,即旋转角速度ωz为0.05π。;
6)为了便于观察,设置检测概率小于0.8的区域为检测盲区。
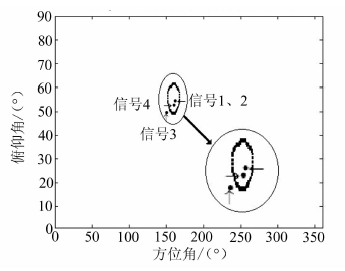
以欺骗信号1为参考信号,可以理论性计算得到如图 5所示的检测盲区划分。图 5中,r为0.59。
|
| 图 5 各路信号位置及第1路信号检测区域 Fig. 5 Signal Position and the First Signal Detection Area |
由图 5可知,方位角/俯仰角为(148°,50°)的信号3在检测盲区外,其余信号均在检测盲区内。并且[3,1]信号载波双差检测的检测概率理论计算值为0.999 9,检测门限为22.050 3。[4,1]信号和[2,1]信号由理论计算得到的检测概率分别为0.037 3和0.010 4,相应检测门限分别为0.076 0和0.020 1。
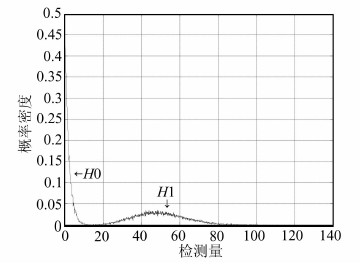
采用蒙特卡洛仿真方法获得[3,1]信号检测时的检测量分布,结果如图 6所示。可见,仿真得到[3,1]信号在设定检测门限下的检测概率为0.999 9,与理论检测概率值吻合。
|
| 图 6 [3,1]信号检测量分布的蒙特卡洛仿真 Fig. 6 Distribution of [3,1] Signal Test Statistic Generated by Monte Carlo Simulation |
同样采用蒙特卡洛方法进行检测量分布的仿真,可以得到设定门限下[4,1]信号和[2,1]信号的检测概率分别为0.036 8和0.010 1,都处于检测盲区内,与理论分析结果一致。
以上仿真结果验证了本文所提检测方法的正确性。
6 结语本文针对单发射天线的欺骗干扰条件,提出了基于旋转天线载波相位双差的欺骗干扰检测技术,得到了以下结论。
1)给出了利用旋转天线输出载波相位测量值双差进行欺骗干扰检测的原理,并推导了基于非相关差分序列的GLRT检测方法;
2)分析表明,增大观察矩阵中的r、sin2ωz和N都将提升旋转天线方法的检测性能,并结合工程实际背景,指出增加数据长度是提升检测性能的必然选择;
3)定义了比较全局检测性能的检测盲区,并可用于限制检测性能的下降。
| [1] | Huang Long, Tang Xiaomei, Wang Feixue. Anti-spoofing Techniques for GNSS Receiver[J]. Geomatics and Information Science of Wuhan University, 2011, 36(11):1344-1347(黄龙, 唐小妹, 王飞雪. 卫星导航接收机抗欺骗干扰方法研究[J]. 武汉大学学报·信息科学版, 2011, 36(11):1344-1347) |
| [2] | Jafarnia-Jahromi A, Broumandan A, Nielsen J, et al. GPS Vulnerability to Spoofing Threats and a Review of Anti-spoofing Techniques[J]. International Journal of Navigation and Observation, 2012:1-16 |
| [3] | Dovis F. Recent Trends in Interference Mitigation and Spoofing Detection[J]. International Journal of Embedded and Real-Time Communication Systems(IJERTCS), 2012, 3(3):1-17 |
| [4] | Nielsen J, Broumandan A, Lachapelle G. Spoofing Detection and Mitigation with a Moving Handheld Receiver[J]. GPS World Magazine, 2010, 21(9):27-33 |
| [5] | Nielsen J, Broumandan A, Lachapelle G. GNSS Spoofing Detection for Single Antenna Handheld Receivers[J]. Navigation, 2012, 58(4):335-344 |
| [6] | Broumandan A, Jafarnia-Jahromi A, Dehghanian V, et al. GNSS Spoofing Detection in Handheld Receivers Based on Signal Spatial Correlation[C]. Position Location and Navigation Symposium(PLANS), IEEE/ION, Myrtle Beach, SC, 2012 |
| [7] | Zhang Xin, Pang Jing, Su Yingxue, et al. Spoofing Detection Technique on Antenna Array Carrier Phase Double Difference[J]. Journal of National University of Defense Technology, 2014, 36(4):55-60(张鑫, 庞晶, 苏映雪, 等. 天线阵载波相位双差的欺骗干扰检测技术[J]. 国防科技大学学报, 2014, 36(4):55-60) |
| [8] | Chen Pei. Attitude Determination Algorithms for Spinning Satellites Using Single Antenna GPS Receiver and MEMS Gyro[J]. Aerospace Science and Technology, 2013, 26(1):10-15 |
| [9] | Miao Shangchao, Wu Pengju. Precision Comparing Between Common Control Survey and GPS Control Survey[J]. Shanxi Architecture, 2008, 34(35):19-21(苗尚朝, 吴鹏举. 常规控制测量与GPS控制测量点位精度比较[J]. 山西建筑, 2008, 34(35):19-21) |
| [10] | Huang Long, Gong Hang, Zhu Xiangwei, et al.Research of Re-radiating Spoofing Technique to GNSS Timing Receiver[J]. Journal of National University of Defense Technology, 2013, 35(4):93-96(黄龙, 龚航, 朱祥维, 等. 针对GNSS授时接收机的转发式欺骗干扰技术研究[J]. 国防科技大学学报, 2013, 35(4):93-96) |
| [11] | Song Hua, Yuan Hong.Simulation of GPS IF Signal in a Spinning State[J]. Computer Simulation, 2009, 26(3):87-90(宋华, 袁洪. 旋转状态下GPS中频信号仿真研究[J]. 计算机仿真, 2009, 26(3):87-90) |
| [12] | Steven M K. Fundamentals of Statistical Signal Processing, Volume Ⅱ:Detection Theory[M]. Prentice Hall:Pearson Education, 1998 |
 2016, Vol. 41
2016, Vol. 41


