文章信息
- 沙海, 陈华明, 吕志成, 李峥嵘, 欧钢
- SHA Hai, CHEN Huaming, LV Zhicheng, LI Zhengrong, OU Gang
- 一种新的高动态条件下实时高精度伪距计算方法
- A New Method of Real-time High Precision Pseudorange Calculation in High Dynamic Circumstance
- 武汉大学学报·信息科学版, 2016, 41(4): 523-528
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 523-528
- http://dx.doi.org/10.13203/j.whugis20140094
-
文章历史
- 收稿日期: 2014-12-25

2. 北京卫星导航中心, 北京, 100094
2. Beijing Satellite Navigating Center, Beijing 100094, China
伪距是GNSS接收机对卫星信号的一个最基本的距离测量值,也是GNSS仿真系统需要获取的最重要的观测数据。在GNSS导航模拟器、干扰信号源等仿真设备中,伪距计算方法是在已知接收机位置和信号接收时间的基础上,通过迭代计算卫星轨道、各类误差项等得到伪距的收敛解[1, 2, 3]。然而随着GPS、GLONASS(Global Navigation Satellite System)、GALILEO和北斗卫星导航系统的不断发展和广泛应用,要求GNSS仿真系统具有全导航星座仿真能力,甚至还包括星间链路仿真,这对伪距的实时计算能力提出很大挑战。另一方面,为了满足弹载、箭载或星载等高动态仿真场景下的测试需求,仿真设备的信号处理部分通常采用三阶DDS(direct digital synthesizer)模型作为伪距变化模型(又称多普勒模型)[4, 5],该模型的本质是伪距的三阶泰勒级数展开函数。由于模型误差、频率控制字量化误差等因素的影响,需要在较小间隔下(如20 ms)计算伪距及其各阶导数,用于更新三阶DDS模型参数[6],这也是伪距计算的重要环节。因此,如何在高动态条件下,解决精度与计算量的矛盾,实现实时高精度的伪距计算,成为当前GNSS仿真测试技术领域的研究热点。
文献[1]通过对卫星、接收机载体运动规律的解析式建模,得到伪距及其各阶导数,但该方法不适用于仅有用户位置坐标值的情况;文献[7]提出了迭代计算与插值计算相结合的伪距计算方法,通过分别计算伪距几何距离和误差项的各阶导数近似得到伪距的各阶导数信息,但精度较低;文献[8]以用户位置坐标作为输入,利用开普勒轨道根数计算卫星位置,改进了伪距计算方法,并提出采用三次样条函数计算伪距及其各阶导数的方法。但该方法需要获得一段时间内多个伪距值才能保证计算精度,严重影响了算法实时性。英国Spirent公司、美国Aeroflex公司都已推出各自的高动态GNSS导航信号模拟器,但出于技术保密,相关资料较少。文献[1]简要介绍了美国空军组织的GPS模拟器增强验证测试计划(Enhanced Validation Test Plan,EVTP),给出了用户接收机运动轨迹,这将作为本文的高动态仿真测试场景。
由此可见,传统的伪距计算方法在算法实时性方面还存在不足,为此,本文在分析伪距计算方法的基础上,通过优化计算步骤减少伪距计算时间。同时,针对伪距及其各阶导数的计算,提出一种基于三阶Hermite插值的伪距计算方法,该方法计算精度高,且仅需相邻两个节点的伪距及其导数信息,算法实时性得到极大提高。
1 伪距计算方法GNSS仿真系统中,伪距计算方法是根据接收机收到卫星信号的时间反推卫星信号发射时间,进而求得该仿真时刻下的伪距值。设仿真时刻t,接收机收到卫星在ts时刻发射的卫星信号,则该时刻下接收机测得的伪距ρ可表示为[2]:
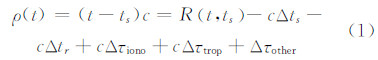
式中,R(t,ts)为卫星到接收机的几何距离;c为光速;Δts为卫星钟差;Δtr为相对论效应延迟;Δτiono、Δτtrop分别为电离层和对流层延迟;Δτother为其他误差。
伪距计算方法本质上可以看作求解卫星发射时刻ts的一元方程求根的数学问题,可将式(1)改写为如下形式:
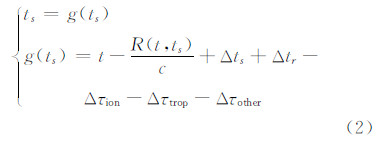
该一元方程可以采用数值计算方法进行求解,考虑到算法实现的复杂性,工程中常采用定点迭代法[9]计算,即给定卫星发射时间的初始值,根据式(2)计算得到新的发射时间,然后通过多次迭代,直至与上次计算值作差后小于误差门限值停止。为了避免出现多次迭代计算,还会限制最大迭代次数。伪距计算方法的具体流程如图 1所示。

|
| 图 1 伪距计算方法流程 Fig. 1 Pseudorange Calculation Process |
根据伪距计算方法的计算步骤,为了进一步减少计算量,提高算法的实时性,可以从以下两个方面对伪距计算过程进行优化。
(1) 使用插值拟合算法计算卫星位置
虽然卫星广播星历、动力学轨道积分方法可以求解任意时刻的卫星位置,但其计算量较大,特别是动力学轨道积分方法计算各种摄动力模型时十分耗时。一种合理的优化方法是采用卫星广播星历或动力学积分方法计算一定时间间隔的轨道数据,然后通过插值拟合算法计算任意时刻的卫星位置。具体实现方法参见文献[10, 11, 12]。
(2) 调整误差延迟量计算顺序
电离层延迟、对流层延迟与接收机位置及卫星仰角有关,而初始仰角与迭代后仰角相比变化量通常很小。卫星钟差相对论效应延迟通常为cm量级,其初始值与迭代后的值相比变化量更小。因此,可以考虑在迭代伪距计算过程中,仅初始化计算电离层延迟、对流层延迟和卫星钟差相对论效应延迟,不重复更新,减少计算量。
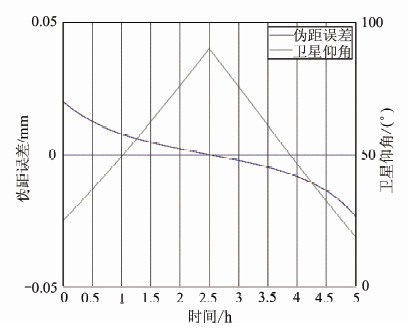
为了验证优化方法的合理性,采用仿真方法分析优化方法的伪距计算误差。仿真时,分别计算5 h内,时间间隔为1 ms的传统高精度伪距计算方法和优化方法的伪距值,并作差得到优化算法的误差。其中卫星轨道采用文献[10]提出的插值算法,其时间间隔为120 s,电离层延迟使用Klobuchar模型,对流层延迟使用Hopfield模型。仿真结果如图 2所示。
|
| 图 2 伪距优化算法计算误差 Fig. 2 Computation Error of Optimized Arithmetic |
由图 2可知,在采用优化方法计算伪距时,最大计算误差仅为3×10-5m,且出现在仰角为90°时,这较mm级伪距计算精度而言完全可以忽略。进一步对优化方法的计算时间进行分析,得出优化方法的计算时间较传统方法减少了约20倍。这比文献[10]的结论略高,说明采用插值算法计算卫星轨道在减少伪距计算时间方面发挥了显著作用,同时调整误差延迟量的计算顺序也进一步减少了计算时间。
3 基于三阶Hermite插值方法原理 3.1 伪距变化模型采用伪距变化模型计算伪距值,一方面可以减少伪距计算量[7],另一方面更新硬件实现时的三阶DDS的频率控制字[8]。忽略高次项,伪距变化模型为:
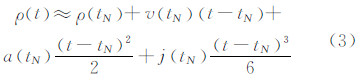
式中,tN为更新时刻;v(tN)为tN时刻的视向速度;a(tN)为加速度;j(tN)为加加速度。
3.2 三阶Hermite插值算法采用三阶Hermite插值算法计算伪距时,只需已知相邻两个节点处的伪距及其变化率便可求得区间内任意点的伪距值。采用三阶Hermite插值算法后的伪距变化模型可以表示为:
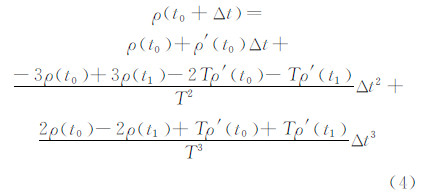
式中,ρ(t0)、ρ′(t0)、ρ(t1)和ρ′(t1)分别为节点t0、t1处的伪距值及其一阶导数;T=t1-t0为等距区间的时间间隔,Δt∈(0,T)。对式(4)分别求导,可得式(3)所需的更新参数为:
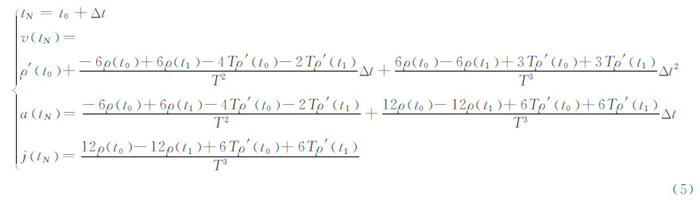
根据§3.2分析,采用三阶Hermite插值算法时,需要已知节点处的伪距一阶导数。文献[7]在分别求得卫星、用户速度的基础上,采用近似方法计算伪距导数,其在高动态场景下误差较大。为此,本文提出利用二阶拉格朗日插值多项式的插值型求导公式[10]计算节点处的伪距导数的方法。具体为,在较小时间步长h下,分别计算ti=t0+ih (i=0,1,2)时的伪距值ρ(ti),则其对应的拉格朗日插值多项式为:
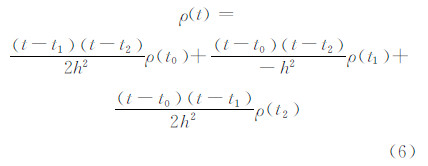
对t求导,并代入t0可得:
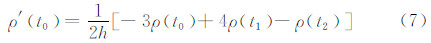
采用基于三阶Hermite插值伪距计算方法时,计算伪距导数中的步长h和等距区间时间间隔T的选取对计算精度影响较大。时间间隔选取较大时,可以提高算法的实时性,但计算精度会有所下降;时间间隔较小时,虽然可以提高计算精度,但算法的计算量明显增大,并且时间间隔减小到一定程度时,还会出现计算精度增大的情况。因此,为了方便实际工程应用,采用仿真手段分析不同步长h和时间间隔T的条件下伪距计算精度,便于根据要求进行选择。
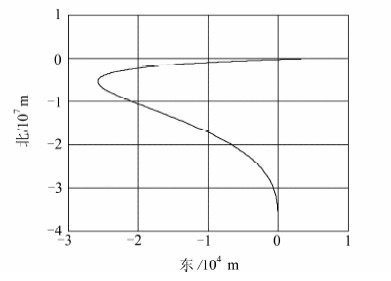
仿真中选取GPS系统PRN01卫星2013年1月23日0时的广播星历作为卫星轨道模型数据。伪距计算时,电离层模型采用Klobuchar模型,对流层模型采用Hopfield模型,模型参数从广播星历中获取。用户轨迹采用文献[13]提供的高动态测试场景,其站心坐标系下东、北方向的轨迹如图 3所示。仿真时长为5 min。
|
| 图 3 EVPT计划高动态用户轨迹 Fig. 3 High Dynamic User Track in EVPT Plan |
采用二阶拉格朗日多项式的插值型求导公式计算伪距导数时,在h=0.001 s、0.005 s、0.01 s、0.05 s的条件下,伪距误差如表 1所示。其中,仿真时选取时间间隔T为1 s,并且每1 ms比较所提方法与直接精确计算的伪距误差。
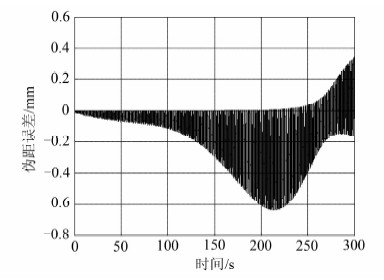
由表 1可知,伪距计算误差随着步长h的增大而增加,当h=0.001 s时,伪距最大误差小于1 mm,满足mm量级的伪距精度要求。其对应的伪距计算误差如图 4所示。
| 步长h/s | 误差最大值/mm | 标准差/mm |
| 0.001 | 0.638 | 0.172 |
| 0.005 | 1.270 | 0.329 |
| 0.01 | 1.275 | 0.334 |
| 0.05 | 4.487 | 1.705 |
|
| 图 4 h=0.001 s时的伪距误差 Fig. 4 Pseudorange Error in h=0.001 s |
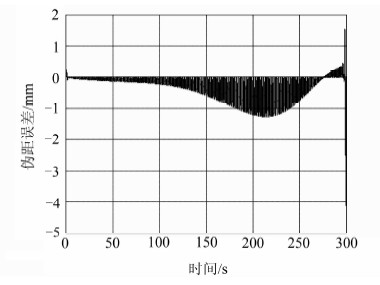
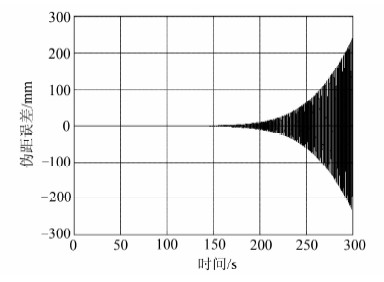
选取不同时间间隔T=0.1 s、0.5 s、1 s和2 s,对新方法的计算误差进行分析,同时采用同样条件下的近似法[7]和三阶样条插值法[8]的计算结果作对比。对于所提方法,步长h为0.001 s,同样每1 ms比较不同方法与直接精确计算的伪距误差。图 5~7分别给出了T=1 s时的各种方法伪距计算误差。
|
| 图 5 T=1 s时的三阶样条插值法伪距误差 Fig. 5 Pseudorange Error of Third-Order Spline Interpolation Method in T=1 s |
|
| 图 6 T=1 s时的近似法伪距误差 Fig. 6 Pseudorange Error of Approximate Method in T=1 s |
|
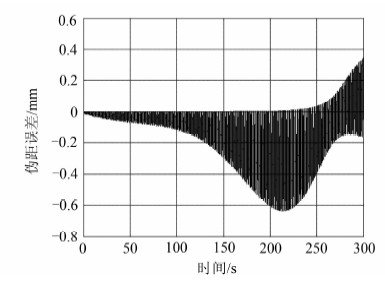
| 图 7 T=1 s时的本文方法伪距误差 Fig. 7 Pseudorange Error of the Proposed Method in T=1 s |
由图 5可以看出,对于三次样条插值法,其伪距计算误差在仿真开始和结束一小段时间内均出现跳变,特别是结束阶段,误差明显增大。而对于近似法,由图 6可知,由于高动态场景下速度计算误差较大,导致伪距误差不断增加,远远大于1 mm的精度要求。而本文所提方法,如图 7所示,仿真时段内没有出现大的误差跳变,计算误差也是最小的。当T取其他时间时,得到的也是类似结果。
进一步对仿真结果进行统计分析,得到表 2中结果。由表 2可以看出,随着时间间隔T的增大,三种方法的计算误差也相应增大。其中,近似法的误差最大,无法满足高动态条件下的伪距计算精度要求;三阶样条插值法在T=0.1 s时具有最高的精度,但随着T的增大,精度明显低于本文方法,可见三阶样条插值法的精度与计算点的个数密切相关。而本文方法只需已知两个节点处的伪距及其导数信息,当T=1 s时,本文方法最大伪距误差仅为0.638 mm,满足伪距精度mm级的要求。综合计算精度与实时性要求,选择时间间隔T=1 s,用于高动态条件下的伪距计算。
| T/s | 计算方法 | 最大误差/mm | 标准差/mm |
| 三阶样条法 | 0.026 | 0.003 | |
| 0.1 | 近似法 | 23.705 | 4.354 |
| 本文方法 | 0.273 | 0.019 | |
| 三阶样条法 | 0.272 | 0.022 | |
| 0.5 | 近似法 | 118.909 | 21.772 |
| 本文方法 | 0.253 | 0.055 | |
| 三阶样条法 | 4.132 | 0.369 | |
| 1 | 近似法 | 238.892 | 43.562 |
| 本文方法 | 0.638 | 0.172 | |
| 三阶样条法 | 64.670 | 6.427 | |
| 2 | 近似法 | 484.031 | 87.435 |
| 本文方法 | 20.275 | 5.271 |
由于近似法的计算精度较差,在对本文方法进行算法实时性分析时,将仅与三阶样条法进行比较。本文方法与三阶样条方法在算法实时性方面比较,优势主要体现在以下两个方面。
(1) 使用本文方法时,只需已知两个节点处的伪距及其导数信息即可;而三阶样条法为了保证计算精度,需要已知多个节点处的伪距信息。当用户位置实时由外部提供应用场景,例如飞行训练模拟器等,需要根据用户实时操作产生位置时,三阶样条法会出现较大的延迟反应时间,而本文方法反应时间则明显较短。
(2) 使用本文方法时,需要计算两个节点处伪距及其导数信息,根据§3.3伪距导数计算方法可知,一共需要计算6个不同时刻的伪距值;而采用三阶样条法,通常需要计算60个不同时刻的伪距值[8]。由此可以得出,本文方法的计算量仅为三阶样条方法的10%。
5 结 语本文针对GNSS高动态仿真测试条件下实时高精度的伪距计算需求,分析了现有伪距计算方法的不足,提出了一种基于三阶Hermite插值的伪距计算方法。首先,通过分析传统伪距计算方法流程,提出采用插值算法计算卫星轨道,并将电离层延迟、对流层延迟等误差项调整至迭代过程前计算的优化方法。通过仿真分析,在仅损失3×10-5 m的伪距精度条件下,显著减少了伪距计算量,提高算法的实时性。同时,针对硬件平台需要频繁更新伪距变化模型参数,提出采用三阶Hermite插值算法计算伪距,该算法只需已知两个节点处的伪距及其导数信息,即可计算区间内任意时刻的伪距值,算法实时性及精度均优于现有方法。其中,伪距导数采用二阶拉格朗日插值多项式的插值型求导公式计算。高动态条件下的仿真结果表明,在步长h为0.001 s、时间间隔T为1 s时,最大伪距误差为0.638 mm,标准差为0.172 mm。
| [1] | Zhao Junxiang. The Study on Mathematical Model of High Dynamic and Intelligent GPS Satellite Signal Simulator's Software[D]. Beijing:Beijing University of Aeronautics and Astronautics, 2003(赵军祥. 高动态智能GPS卫星信号模拟器软件数学模型研究[D]. 北京:北京航空航天大学, 2003) |
| [2] | Lv Zhicheng. The Research of the High Dynamic Satellite Signal Simulator's Software[D]. Changsha:National University of Defense Technology, 2006(吕志成. 高动态卫星导航信号模拟器软件研究[D]. 长沙:国防科学技术大学, 2006) |
| [3] | Liu Xiaoli, Chen Dongdong, He Xi, et al. Simulation and Testing of FPLL Carrier Tracking Loops with High Dynamic GPS Signals[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11):1329-1333(刘晓莉, 陈东东, 贺喜, 等. FPLL载波跟踪环仿真及高动态GPS信号测试[J]. 武汉大学学报·信息科学版, 2014, 39(11):1329-1333) |
| [4] | Qi Wei, Chang Qing, Zhang Qishan, et al. Arithmetic of Doppler Simulation in High Dynamic Signal Simulator[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5):1252-1257(齐巍, 常青, 张其善, 等. 高动态信号模拟器中的多普勒模拟算法[J]. 航空学报, 2008, 29(5):1252-1257) |
| [5] | Zhang B, Liu G B, Jiao W, et al. High-order DDFS Applied in Simulated High Dynamic GNSS Signal Synthesis[C]. The 9th International Conference on Electronic Measurement & Instruments, Beijing, 2009 |
| [6] | Song Y Y, Zhou H, Zeng T, et al. Algorithm and Realization of High Dynamic Satellite Signal Doppler Simulation Based on FPGA[C]. International Technical Meeting of the Satellite Division of the Institute of Navigation, San Diego, CA, 2010 |
| [7] | Luo Yihong, Wang Wei, Xi Xiaoning. Real-time Simulation of Pseudo-range Generation of Navigation Satellite Signal Simulator[J]. Computer Simulation, 2009, 26(7):77-80(罗益鸿, 王威, 郗晓宁. 导航卫星信号模拟器伪距生成实时仿真研究[J]. 计算机仿真,2009, 26(7):77-80) |
| [8] | Liu Min, Wu Siliang. Method of High Accuracy Pseudorange Generation for Real-time High Dynamic GNSS Signal Simulator[J]. Transactions of Beijing Institute of Technology, 2011, 31(9):1053-1057(刘旻, 吴嗣亮. 实时高动态GNSS信号模拟器高精度伪距生成方法[J]. 北京理工大学学报, 2011, 31(9):1053-1057) |
| [9] | Ding Lijuan. Numerical Computation Method[M]. Beijing:Beijing Institute of Technology Press, 1997(丁丽娟. 数值计算方法[M]. 北京:北京理工大学出版社, 1997) |
| [10] | Korvenoja P, Piche R. Efficient Satellite Orbit Approximation[C]. The 13th International Technical Meeting of the Satellite Division of the Institute of Navigation, Salt Lake City, USA, 2000 |
| [11] | Horemuz M, Andersson J V. Polynomial Interpolation of GPS Satellite Coordinates[J]. GPS Solution, 2006, 10:67-72 |
| [12] | Zheng Kun, Dong Xurong, Yang Yang, et al. A New Time Synchronization System Based on the GEO[J]. Geomatics and Information Science of Wuhan University, 2014, 39(10):1163-1168(郑坤, 董绪荣, 杨洋, 等. 一种基于GEO星间链路的导航系统时间同步新体制[J]. 武汉大学学报·信息科学版, 2014, 39(10):1163-1168) |
| [13] | Thompson E. An Initial Look at Validating GPS Simulators Through the Enhanced Validation Test Plan[C]. The ION NTM, Salt Lake City, 2001 |
 2016, Vol. 41
2016, Vol. 41



