2016, Vol. 41文章信息
- 周东旭, 周兴华, 张化疑, 王朝阳, 唐秋华
- ZHOU Dongxu, ZHOU Xinghua, ZHANG Huayi, WANG Zhaoyang, TANG Qiuhua
- 利用GPS连续观测进行中国沿海验潮站地壳垂直形变分析
- Analysis of the Vertical Deformation of China Coastal Tide Stations Using GPS Continuous Observations
- 武汉大学学报·信息科学版, 2016, 41(4): 516-522
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 516-522
- http://dx.doi.org/10.13203/j.whugis20140714
-
文章历史
- 收稿日期: 2015-11-13
2. 国家海洋局第一海洋研究所, 山东 青岛, 266061
2. The First Institute of Oceanography, State Oceanic Administration, Qingdao 266061, China
长期验潮数据作为当前海平面变化研究的重要数据源，易受验潮站地壳垂直形变的影响。确定和分离验潮站地壳垂直形变，对维护验潮基准和研究海平面真实变化等具有重要意义。
目前，验潮站的地壳垂直形变受到国内外相关机构和学者的密切关注，并采用诸多技术方法对其进行修正或分离。政府间气候变化专门委员会(Intergovernmental Panel on Climate Change,IPCC)在全球范围内采用冰后回弹模型(Glacial Isostatic Adjustment,GIA)修正验潮站地壳垂直形变[1]；国际GNSS服务(International GNSS Service,IGS)机构成立了TIGA(Tide Gauge Benchmark Monitoring)项目组，利用全球沿海区IGS站监测验潮站的基准变化；Buble[2]、Itthi[3]、Fenoglio-Marc[4]、Lin[5]、Mazzotti[6]、Bell[7]、Richard[8]和Wöppelmann[9]等人利用GPS数据分析了北美、欧洲南部、泰国湾、印度尼西亚、新西兰惠灵顿等地区验潮站的地壳垂直形变，为研究区域海平面变化提供了重要参考。我国于2012年启动的国家重大科学研究计划 “近百年极地冰层和全球及典型区域海平面变化机理精密定量研究”，将中国沿海验潮站的地壳垂直形变作为重要研究内容之一；国家海洋局使用精密水准或GPS技术，对我国一些长期验潮站的验潮基点进行了水准联测；焦文海[10]、刘根友[11]等人利用GPS数据对我国6个验潮站的地壳垂直形变进行了初步分析，赵明才[12]等人基于均衡理论推求了中国沿海17个长期验潮站的地壳垂直运动。
由于我国各验潮站水准联测时采用的联测基点不同，联测时间不一致，无法在全国范围内统一基准下分析各验潮站的地壳垂直形变；文献[10, 11]采用的GPS数据观测时间较短，难以精确反映验潮站的地壳形变；而均衡理论受站点分布、站间距离等因素影响，具有较严格的适用条件。目前，我国对沿海长期验潮站地壳垂直形变现状的了解仍相对匮乏，制约着我国近海海平面变化研究工作的深入开展，在统一基准下分析各海区验潮站的地壳垂直形变已日趋迫切。
针对上述问题，本文收集了中国沿海 22个长期验潮站2009~2013年的并址GPS连续观测数据，在统一基准下更为精细地研究验潮站地壳垂直形变特征；并利用实测潮汐资料，分析验潮站地壳形变对区域海平面变化的影响。
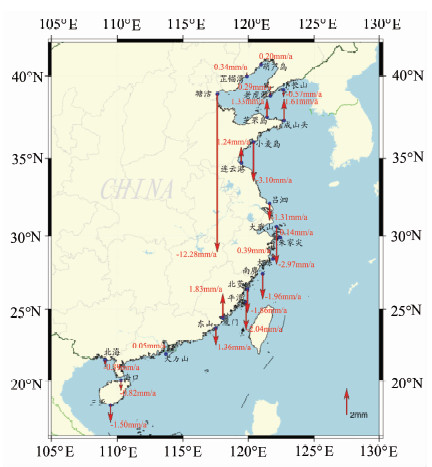
1 数据与分析方法 1.1 数据来源2009年始，国家海洋局在沿海56个长期验潮站陆续增设GNSS观测设施(GNSS接收机类型TOPCON TPS NET-G3，天线类型TPSCR.G3)，建立了中国沿海GNSS业务化观测系统(2010年建成)。本文收集了该系统22个验潮站2009~2013年期间的GPS数据(验潮站分布见图 1)，分析其地壳垂直形变。
|
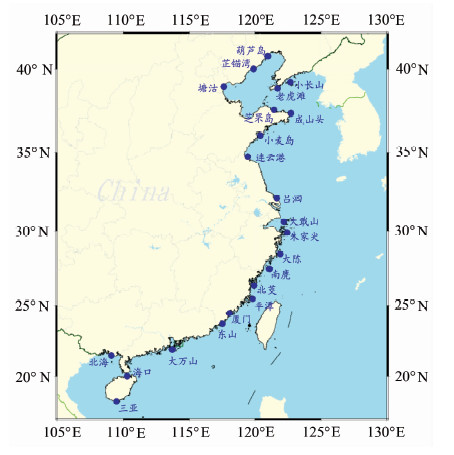
| 图 1 验潮站位分布示意图 Fig. 1 Distribution of the Tide Stations |
GPS数据处理采用与文献[13]相类似的方法，即首先利用BERNESE5.0软件的GPSEST模块，联合中国境内及其周边的BJFS、CHAN、SHAO、XIAN、WUHN、KUNM、TNML、DAEJ、NTUS、PIMO等10个IGS站的同期数据，解算收集到的GPS原始数据，获取其单日解；然后利用ADDNEQ2模块和选定的10个IGS站通过相似变换处理单日解，将解算结果统一到ITRF2008参考框架；最后将各站的空间直角坐标归算至站心坐标系下。
1.3 坐标时间序列精度评价本文采用长期重复性[14]和均连方差[15]等精度评定指标，分析22个验潮站2009~2013年的位置坐标解算精度。长期重复性和均连方差计算公式分别为式(1)、式(2)，统计结果详见表 1。
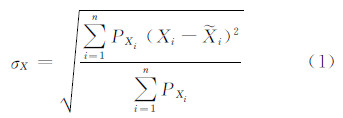
式中，σX表示坐标X的重复性；Xi表示i测段的坐标；PXi表示i测段坐标的中误差平方倒数；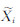 
表示i测段对应的坐标线性拟合值；n表示测段个数。
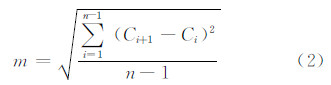
式中，m表示坐标分量的均连方差；Ci为第i时段的坐标分量；n为时段个数。
| 测站 | 长期重复性 | 均连方差 | ||||
| E | N | U | E | N | U | |
| 小长山 | 4.7 | 3.3 | 6.8 | 4.1 | 4.1 | 8.2 |
| 老虎滩 | 3.6 | 3.2 | 6.1 | 3.6 | 3.8 | 7.8 |
| 葫芦岛 | 3.7 | 3.3 | 6.5 | 3.8 | 4.0 | 7.7 |
| 止锚湾 | 3.1 | 3.0 | 6.1 | 3.3 | 3.8 | 6.8 |
| 塘沽 | 6.9 | 8.1 | 9.0 | 4.7 | 4.5 | 8.6 |
| 芝罘岛 | 3.3 | 2.8 | 5.7 | 3.9 | 3.6 | 6.7 |
| 成山头 | 3.6 | 2.6 | 7.2 | 3.4 | 3.3 | 6.4 |
| 小麦岛 | 3.2 | 3.2 | 5.8 | 3.3 | 3.2 | 6.3 |
| 连云港 | 3.2 | 3.2 | 6.3 | 3.8 | 3.9 | 6.1 |
| 吕泗 | 3.7 | 3.0 | 5.3 | 4.1 | 3.6 | 6.5 |
| 大戢山 | 3.1 | 3.0 | 6.9 | 4.1 | 3.3 | 7.1 |
| 朱家尖 | 3.0 | 3.4 | 7.2 | 3.6 | 3.2 | 6.2 |
| 大陈 | 2.9 | 2.7 | 5.8 | 3.4 | 3.1 | 6.0 |
| 南麂 | 3.3 | 3.4 | 5.8 | 3.5 | 3.5 | 5.9 |
| 北茭 | 3.2 | 2.8 | 5.8 | 3.8 | 3.3 | 6.7 |
| 平潭 | 3.5 | 3.1 | 5.7 | 3.8 | 3.5 | 5.7 |
| 厦门 | 3.2 | 3.3 | 5.1 | 4.1 | 3.7 | 6.2 |
| 东山 | 3.4 | 2.8 | 5.4 | 3.8 | 3.4 | 5.7 |
| 大万山 | 3.4 | 3.3 | 5.9 | 3.7 | 3.3 | 6.0 |
| 北海 | 3.4 | 3.2 | 6.0 | 3.9 | 3.4 | 6.5 |
| 海口 | 3.6 | 3.4 | 5.5 | 3.9 | 3.6 | 5.9 |
| 三亚 | 3.6 | 3.7 | 5.2 | 3.9 | 3.6 | 5.4 |
| 均值 | 3.57 | 3.35 | 6.14 | 3.80 | 3.58 | 6.56 |
由表 1中的统计结果可知，各验潮站长期重复性在E、N、U方向的均值分别为3.57 mm、3.35 mm和6.14 mm，略低于中国地壳运动观测网络和国际同类网的单日重复性精度[16, 17]。各验潮站的均连方差在E、N、U方向的均值分别为3.80 mm、3.58 mm和6.56 mm，与中国地壳运动观测网络数据处理精度相当[15]。
2 验潮站地壳垂直形变分析 2.1 高程序列的周期分析已有研究结果表明，基于GPS连续观测数据得到的高程变化具有一定的周期性。本文采用周期图法(lomb算法)对各验潮站的GPS高程时间序列进行谱分析。Lomb算法可直接对非等间距采样资料进行谱分析，其算法公式如下：
式中，ω为拉普拉斯变化频率响应值；σ为采样误差； x为采样平均值；τ为相移因子，可由
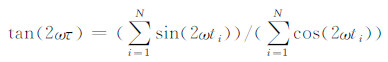
求得。
在周期分析过程中，本文依次对最显著周期进行检测分析[18]，即首先借助一元线性回归拟合从GPS高程时间序列中剔除概略趋势项，得到较平稳的时间序列；然后对平稳时间序列进行最显著周期的检测，并剔除显著周期项获取新的时间序列，再对新时间序列进行最显著周期检测和剔除，重复上述过程直至无显著周期为止；最后以确定的显著周期和GPS高程时间序列作为原始信息重新计算趋势项，获取平稳时间序列，再重复上述最显著周期检测步骤，确定最终周期。在周期分析过程中，采用方差的F检验(α=0.05)法进行周期的显著性检验[18]。各验潮站GPS高程时间序列周期分析结果详见表 2。
| 观测站 | 显著周期 | 观测站 | 显著周期 |
| 小长山 | 0.4、1、2 | 朱家尖 | 0.67、1、1.33、2 |
| 老虎滩 | 0.4、0.5、2 | 大陈 | 0.33、1、1.33、2 |
| 葫芦岛 | 0.4、0.715、1、2 | 南麂 | 0.33、0.5、1、2 |
| 止锚湾 | 0.31、0.5、0.8、1、2 | 北茭 | 0.5、0.8、1、1.33、2 |
| 塘沽 | 0.25、1 | 平潭 | 0.5、0.67、0.8、1、2 |
| 芝罘岛 | 1、2 | 厦门 | 0.25、0.33、0.5、1、1.33 |
| 成山头 | 0.33、0.715、1、2 | 东山 | 0.33、0.5、1 |
| 小麦岛 | 1 | 大万山 | 0.25、0.33、0.5、1 |
| 连云港 | 0.33、1、2 | 北海 | 0.25、0.33、0.715、0.83、1 |
| 吕泗 | 0.33、0.5、1 | 海口 | 0.4、0.5、0.715、1、1.25 |
| 大戢山 | 0.33、1、2 | 三亚 | 0.25、0.33、0.5、0.67、1、1.33 |
表 2统计结果显示，验潮站的高程变化中除包含0.5 a,1 a,2 a等常见变化周期外，还存在0.25、0.33、0.4、0.67、0.715、0.8、1.33 a等其它变化周期。参考图 1中各验潮站位置，0.4 a变化周期主要集中在辽宁沿海验潮站，1.33 a变化周期主要集中在东海区验潮站，0.715 a变化周期主要集中在较大海湾顶部、半岛及岛屿顶端验潮站，0.33 a变化周期则广泛存在各海区的验潮站。
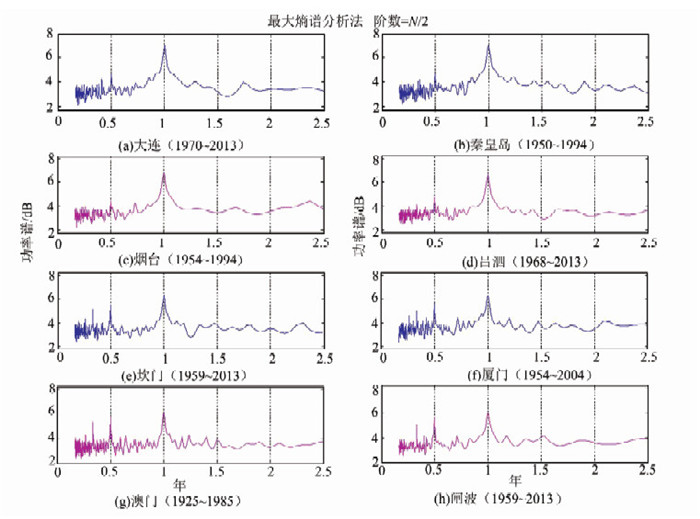
现有研究结果表明海洋潮汐是影响沿海GPS观测的最重要外界因素。本文同时收集大连、秦皇岛、烟台、吕泗、坎门、厦门、澳门、闸坡等8个验潮站的长期验潮月均资料(＞40 a)，分析其潮汐变化周期与验潮站高程变化的关联性(详见图 2)。为便于与高程变化周期比较，图 2中对大于2.5 a的潮汐周期做了截断处理。
|
| 图 2 长期验潮时间序列功率谱分析结果图 Fig. 2 Power Spectrum Analysis of Long Tidal Time Series |
图 2显示，各验潮站的潮汐除具有明显的1 a、0.5 a变化周期外，吕泗、坎门、厦门、澳门站存在一定的0.25 a变化周期；秦皇岛、吕泗、坎门、厦门、澳门、闸坡站存在0.33 a变化周期，且该周期项在东海南部和南海较为显著；大连站存在0.4 a左右的变化周期；烟台、厦门、闸坡站存在0.7 a左右的变化周期；大连和秦皇岛站0.8 a的变化周期也较为显著；此外坎门与厦门站存在微弱的1.33 a变化周期。
表 3中统计了8个验潮站的主要潮汐变化周期(< 2.5 a)与自身或临近验潮站(距离< 100 km)的高程变化周期。统计结果显示，各验潮站的高程变化周期与其临近潮汐变化周期之间具有较好的一致性。本文推测验潮站地壳高程形变所呈现的一些短周期变化可能与潮汐存在某种关联，相关研究有待后续进一步开展。此外，大气、温度等因素也会对验潮站高程周期变化产生一定的影响，在此不做深入探讨。
| 验潮站 | 显著周期 | GNSS观测站 | 距离/km | 相同周期项 |
| 大连 | 0.4、0.5、1 | 老虎滩 小长山 | 0.07 94.156 | 0.4、0.5 0.4、0.5、1 |
| 秦皇岛 | 0.33、0.5、1 | 芷锚湾 | 27.281 | 0.31、0.5、1 |
| 烟台 | 0.5、0.7、1 | 芝罘岛成山头 | 6.921107.331 | 10.5、0.715、1 |
| 吕泗 | 0.25、0.33、0.5、1 | 吕泗 | 6.285 | 0.33、0.5、1 |
| 坎门 | 0.25、0.33、0.5、1、1.33 | 大陈南麂 | 72.79172.47 | 0.33、1、1.330.33、0.5、1 |
| 厦门 | 0.25、0.33、0.5、0.7、1、1.33 | 厦门东山 | 0.00595.873 | 0.25、0.33、0.5、1、1.33 0.33、0.5、1 |
| 澳门 | 0.25、0.33、0.5、1 | 大万山 | 33.01 | 0.25、0.33、0.5、1 |
| 闸坡 | 0.33、0.5、0.7、1 | -- | -- | -- |
根据§2.1的周期分析结果，选用三角多项式模型分离各验潮站GPS高程的周期变化，提取地壳形变趋势，得到各验潮站的地壳垂直形变速率详见图 3和表 4。
|
| 图 3 验潮站地壳垂直形变图 Fig. 3 Vertical Movement of the Tide Stations |
| 测站 | 速率/(mm·a-1) | 测站 | 速率/(mm·a-1) |
| 小长山 | -0.57±0.25 | 朱家尖 | 0.14±0.13 |
| 老虎滩 | 0.29±0.16 | 大陈 | 0.39±0.15 |
| 葫芦岛 | 0.20±0.18 | 南麂 | -1.96±0.14 |
| 止锚湾 | 0.34±0.13 | 北茭 | -1.86±0.17 |
| 塘沽 | -12.28±0.22 | 平潭 | -2.04±0.21 |
| 芝罘岛 | 1.33±0.16 | 厦门 | 1.83±0.25 |
| 成山头 | 1.61±0.15 | 东山 | -1.36±0.29 |
| 小麦岛 | -3.10±0.21 | 大万山 | 0.05±0.16 |
| 连云港 | 1.24±0.16 | 北海 | -0.39±0.17 |
| 吕泗 | -1.31±0.28 | 海口 | -0.82±0.22 |
| 大戢山 | -2.97±0.38 | 三亚 | -1.50±0.14 |
由图 3和表 4可知，我国沿海22个验潮站的地壳垂直形变差异较大，如大万山站年均变化仅0.05 mm，而塘沽站则每年沉降12.28 mm。初步分析认为，塘沽验潮站建在码头上，其高程变化可能受到天津地区地面沉降和码头自身下沉的综合影响。同时，验潮站的地壳形变具有较显著的海区差异，如北海区除小长山、塘沽和小麦岛验潮站，其余5站均以上升为主；东海区相对复杂，验潮站上升与下降趋势交替出现；而南海区除大万山验潮站外，其余3站均以下降为主。此外，验潮站的地壳垂直形变还具有小区域一致性，如辽东湾西侧的芷锚湾与葫芦岛站，山东半岛北部的芝罘岛与成山头站，浙江东部的朱家尖与大陈站，东南沿海的南麂、北茭与平潭站等，均具有相似的形变速率。
地壳均衡理论认为，大部分沿海地区地壳上升和下降运动交替，对于足够长度的滨海地段，总体上升与下降可相互补偿。统计本文22个验潮站的地壳形变速率和为-22.74 mm/a，基于均衡理论无法消除验潮站地壳垂直形变对海平面变化的影响，表明均衡理论具有一定的适用条件。加之我国沿海存在因过量开采地下水等人为因素形成的天津、上海沉降漏斗区，也会对均衡理论在我国沿海的适用性产生影响。
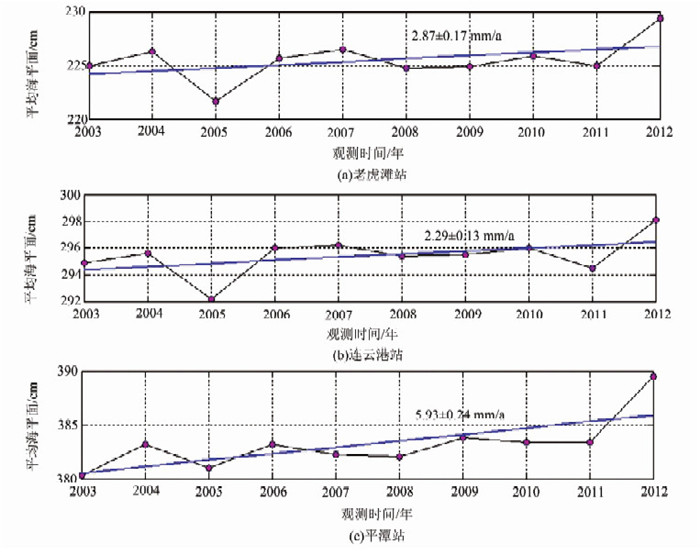
2.3 区域海平面变化修正为分析验潮站地壳垂直形变对海平面变化的影响，本文收集了老虎滩、连云港、平潭验潮站2003~2013年的潮汐年均数据，采用一元线性回归方程提取海平面变化趋势。
图 4中“·”表示验潮站的原始观测数据；蓝色线代表各验潮站海域的海平面上升趋势。图 4中，平潭海域每年上升5.93 mm，连云港海域每年上升2.29 mm，老虎滩海域每年上升2.87 mm，平潭海域海平面的上升速率比其他两处海域高约3 mm/a。
|
| 图 4 验潮站海域相对海平面变化 Fig. 4 Relative Sea Level Change of the Tide Stations |
经验潮站地壳垂直形变修正后，平潭、连云港及老虎滩海域的海平面年上升量依次为3.89 mm、3.53 mm和3.16 mm，三处海域的海面上升速率趋于一致，最大差异为0.73 mm/a，平均速率为3.53 mm/a，高于1980~2013年期间的中国沿海海平面上升速率[19](2.9 mm/a)和1993~2010 a期间的全球平均速率[20](3.2 mm/a)。查阅2003~2013年期间的中国海平面公报，10 a间中国沿海海平面的上升速率升高了0.4 mm(2003年为2.5 mm/a，2013年为2.9 mm/a)，结合本文分析结果可知，我国沿海绝对海平面上升速率高于全球速率，且存在加速上升趋势。
由上述分析可知，在统一基准下研究验潮站地壳垂直形变，可以有效消除沿海地壳形变对区域海平面变化的影响，更为准确地分析中国沿海绝对海平面变化。
3 结 语本文在统一参考基准下，利用近5 a的GPS连续观测数据分析了我国沿海22个验潮站的地壳垂直形变，并利用实测潮汐资料论证了研究验潮站地壳垂直形变的重要意义。
(1) 沿海验潮站的地壳垂直形变除具有0.5 a、1 a、2 a等变化周期，还存在0.25、0.33、0.4 a等疑与潮汐相关的变化周期。
(2) 我国沿海验潮站的地壳垂直形变趋势既具有一定的小区域一致性特征，又存在显著的海区差异，使用均衡理论难以消除其影响。
(3) 在统一基准下研究验潮站地壳垂直形变，可以有效消除沿海地壳形变对区域海平面变化的影响，更为精细地分析沿海海平面变化。
受GPS观测资料限制，本文仅分析了22个验潮站5 a的地壳垂直形变。更为细致的研究有待于采用更多站、更长时段的GPS资料，并结合验潮站的潮汐数据展开。
| [1] | Peltier W R. Global Glacial Isostatic Adjustment and Modern Instrumental Records of Relative Sea Level History[J]. International Geophysics, Sea Level Rise, 2001,75:65-95 |
| [2] | Buble G, Bennett R A, Hreinsdottir S. Tide Gauge and GPS Measurements of Crustal Motion and Sea Level Rise Along the Eastern Margin of Adria[J]. J Geophy Res, 2010, 115:B02404, doi:10.1029/2008JB006155 |
| [3] | Itthi T, Marc N, Wim S, et al. Sea Level Change in the Gulf of Thailand from GPS-corrected Tide Gauge Data and Multi-satellite Altimetry[J]. Global and Planetary Change, 2011, 76:137-151 |
| [4] | Fenoglio-Marc L, Schöne T, Illigner J, et al. Sea Level Change and Vertical Motion from Satellite Altimetry, Tide Gauges and GPS in the Indonesian Region[J]. Marine Geodesy, 2012, 35(sup1):137-150 |
| [5] | Lin J. Correction of Tide Gauge Measurements to Absolute Sea Level by Vertical Motion Solutions[D]. Columbus:Ohio State University, 2000 |
| [6] | Mazzotti S, Jones C, Thomson R E. Relative and Absolute Sea Level Rise in Western Canada and Northwestern United States from a Combined Tide Gauge-GPS Analysis[J]. J Geophy Res, 2008, 113, C11019, doi:10.1029/2008JC004835 |
| [7] | Bell R G, Hannah J.Sea-Level Variability and Trends:Wellington Region[R]. New Zealand Hamilton:National Institute of Water & Atmosphera Research, 2012 |
| [8] | Richard S, Michael C, Dillinger W, et al. Using Global Positioning System-derived Crustal Velocities to Estimate Rates of Absolute Sea Level Change from North American Tide Gauge Records[J]. Journal of Geophysical Research,2007,112:B044-B053 |
| [9] | Wöpelmann G, Marcos M. Coastal Sea Level Rise in Southern Europe and the Nonclimate Contribution of Vertical Land Motion[J]. J Geophy Res, 2012, doi:10.1029/2011JC00746933 |
| [10] | Jiao Wenhai, Wei Ziqing, Guo Hairong,et al. Determination of the Absolute Rate of Sea Level by Using GPS Reference Station and Tide Gauge Data[J]. Geomatics and Information Science of Wuhan University, 2004,29(10):901-904(焦文海, 魏子卿,郭海荣,等. 联合GPS基准站和验潮站数据确定海平面绝对变化[J]. 武汉大学学报·信息科学版,2004,29(10):901-904) |
| [11] | Liu Genyou, Zhu Yaozhong, Xu Houze,et al. Study on Height Changes of Chinese Tide Gauges by GPS[J]. Geomatics and Information Science of Wuhan University, 2005,30(12):1044-1047(刘根友,朱耀仲,许厚泽,等.GPS监测中国沿海验潮站垂直运动观测研究[J]. 武汉大学学报·信息科学版,2005,30(12):1044-1047) |
| [12] | Zhao Mingcai, Ma Jirui, Han Guijun,et al. Calculation Vertical Crustal Movement in Coastal Area of China from Sea Level Changes[J]. Hydrographic Surveying and Charting, 2001,3:9-13(赵明才,马继瑞,韩桂军,等.由海平面变化推求中国沿海地区地壳垂直运动[J]. 海洋测绘,2001,3:9-13) |
| [13] | Wang Wei. Study on Present-day Crustal Movement with GPS Data and Modeling the Active Deformation in the Chinese Mainland[D].Beijing:Institute of Geophysics, China Earthquake Administration, 2013(王伟. 中国大陆现今地壳运动的GPS分析与构造变形模拟[D]. 北京:中国地震局地球物理研究所,2013) |
| [14] | Larson K M, Agnew D C. Application of Global Positioning System to Crustal Deformation Measurements, 1:Precision and Accuracy[J]. J Geophys. Res., 1991, 96:16547-16565 |
| [15] | Liu Guangming, Wei Ziqing, Tang Yingzhe, et al. Data Processing of Maintaining Geocentric Coordinates System in China[J]. Science of Surveying and Mapping, 2008, 33(4):35-38(刘光明,魏子卿,唐颖哲,等. 维持中国地心坐标系的基准站数据处理[J]. 测绘科学,2008, 33(4):35-38) |
| [16] | Wang Min, Zhang Zusheng, Xu Mingyuan, et al. Data Processing and Accuracy Analysis of National 2000'GPS Geodetic Control Network[J]. Chinese Journal of Geophysics, 2005, 48(4):817-823(王敏,张祖胜,许明元,等.2000国家GPS大地控制网的数据处理和精度评价[J]. 地球物理学报,2005, 48(4):817-823) |
| [17] | Gu Guohua, Niu Hongye, Meng Guojie, et al. Advances in Data Processing of the Crustal Movement Observation Network in China[J]. GNSS World of China, 2001, 26(1):5-13(顾国华,牛红叶,孟国杰,等. 中国地壳运动观测网络GPS数据处理进展[J]. 全球定位系统,2001, 26(1):5-13) |
| [18] | Xia Huayong, Li Shuhua. A Grey Model with Periodic Term for Sea-level Analysis and Its Application to Guangxi Coast[J]. Acta Oceanologica Sinica, 1999,21(2):9-17(夏华永, 李树华.带周期项的海平面变化灰色分析模型及广西海平面变化分析[J].海洋学报,1999,21(2):9-17) |
| [19] | State Oceanic Administration People's Republic of China. Bulletin of the Chinese Sea Level[OL].http://www.coi.gov.cn/gongbao/haipingmian,2014(国家海洋局. 中国海平面公报[OL]. http://www.coi.gov.cn/gongbao/haipingmian,2014) |
| [20] | Intergovernmental Panel on Climate Change. Working Group 1:Climate Change 2013, The Physical Science Basis[R]. Stockholm:IPCC, 2013 |