文章信息
- 汪海洪, 宁津生, 罗志才
- WANG Haihong, NING Jinsheng, LUO Zhicai
- 一种改进的航空重力测量数据处理方法
- An Modified Method for Airborne Gravimetry Data Processing
- 武汉大学学报·信息科学版, 2016, 41(4): 511-515
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 511-515
- http://dx.doi.org/10.13203/j.whugis20140153
-
文章历史
- 收稿日期: 2014-10-14

2. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉, 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan 430079, China
航空重力测量由于具有快速经济、分布均匀、精度良好等优点,已成为获取中高频重力场信息的重要手段,在许多国家和地区得到快速发展和广泛应用[1, 2, 3, 4, 5]。航空重力测量受到载体运动加速度、交叉耦合效应以及厄特弗斯效应等影响,数据处理时必须进行误差改正。载体运动加速度可以利用全球定位系统(GPS)对这些观测数据计算得到,这方面已有许多研究成果[6, 7, 8]。交叉耦合是由仪器不完善引起的,对仪器进行标定即可削弱其影响[9]。国际上先后提出了多种厄特弗斯改正公式,如球近似下的Thompson公式[10]、顾及椭球扁率一阶项的Harlan公式[11]以及椭球近似下的严密公式[2, 12]等。这些厄特弗斯改正公式有一个共同的前提条件,即法线和垂线重合,也就是存在垂线偏差为零的假设。Harlan曾认为这一假设的影响可以忽略不计[11],但是据Wall的估算,当垂线偏差每km的变化率超过1″时,会引起几个mGal甚至几十个mGal的误差[13]。文献[14]对各种厄特弗斯改正公式及其实际使用中出现的问题作了详细讨论,指出在高精度测量要求下,厄特弗斯改正公式的近似处理会造成不可忽略的影响。本文通过将航空重力数据转换到(准)惯性坐标系中进行处理,给出了比航空重力测量的传统方法更为简单严密的改进方法,避免了传统方法中计算厄特弗斯改正的一些近似处理。航空标量重力测量系统一般都有3个相互正交的加速度计,其中2个水平加速度计主要用于维持观测平台与当地水平面平行。改进方法在获得重力垂向分量的同时还能利用这两个水平加速度计的观测值估计重力水平分量。
1 航空重力测量的经典公式在航空标量重力测量系统中,确定重力垂向分量gD采用的标准公式为[1, 2, 15]:

式中,fg是加速度计测定的加速度垂向分量(铅垂线方向),与基准站联测的结果为fg=fz-f0+g0,其中fz是仪器读数,f0是仪器读数初值,g0为基准站重力值;Grv 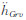 是经杆臂校正后加速度计处的运动加速度向上分量(椭球面法线方向);δgt为倾斜改正,其精确的计算公式可参见文献[16];δgE是厄特弗斯改正,常用的计算公式有Thompson公式[10]和Harlan公式[11],后者相对前者顾及了椭球扁率一阶项的影响。根据文献[14]的计算,忽略地球曲率半径引起的厄特弗斯改正误差可达mGal级。Li通过实验计算了Harlan公式忽略的高阶项误差为μGal级,但是与纬度和航高有复杂的系统相关特性[17]。更为严密的计算公式是基于旋转椭球导出的,即[2, 12]:
是经杆臂校正后加速度计处的运动加速度向上分量(椭球面法线方向);δgt为倾斜改正,其精确的计算公式可参见文献[16];δgE是厄特弗斯改正,常用的计算公式有Thompson公式[10]和Harlan公式[11],后者相对前者顾及了椭球扁率一阶项的影响。根据文献[14]的计算,忽略地球曲率半径引起的厄特弗斯改正误差可达mGal级。Li通过实验计算了Harlan公式忽略的高阶项误差为μGal级,但是与纬度和航高有复杂的系统相关特性[17]。更为严密的计算公式是基于旋转椭球导出的,即[2, 12]:
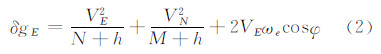
式中,VN和VE分别为载体运动速度的北分量和东分量;N和M分别表示地球椭球卯酉圈和子午圈曲率半径;h是大地高;φ是大地纬度;ωe为平均地球自转速率。如前文所述,所谓的严密公式仍把椭球法线当作实测重力加速度的垂线处理,忽略了垂线偏差的影响。在重力场复杂的地区,垂线偏差对厄特弗斯改正的影响可达mGal级[13]。
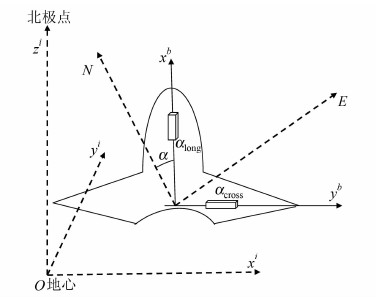
2 改进方法定义载体坐标系b系(以重力仪中心为原点,图 1中体坐标系b的zb和导航坐标系的向下分量指向纸背面构成右手系,图 1所示的{xb,yb,zb}为坐标轴)中的加速度矢量为:

式中,along为沿载体运动方向的加速度分量;across为垂直载体运动方向的加速度分量;adown为经倾斜改正后的加速度计垂向分量观测值,即a<down=fg-δgt,加速度计观测量前面的负号是为了与定义的坐标系方向一致。在(准)惯性坐标系i系[18]下总运动加速度为:

式中,
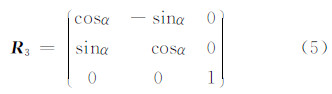
式中,α为图 1所示的飞机航向角;Cni为当地坐标系n系到i系的转换矩阵,表示为:

式中,Cei为地固坐标系e系到i系的转换矩阵:
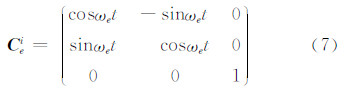
式中,t为时间。Cne为n系到e系的转换矩阵:
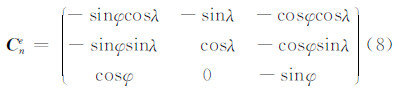
利用定位结果xe,可由式(9)计算出i系下的总运动加速度:

在惯性系中没有科氏力的作用,故最后的引力可表示为[19]:
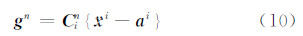
加上离心力效应后重力值为:

Ωiee是由e系相对i系的旋转矢量得到的反对称矩阵[20]。
|
| 图 1 航空重力测量系统及各参考坐标系示意图 Fig. 1 A Diagram of the Airborne Gravimetry System and the Related Reference Frames |
综合式(3)、(4)、(9)~(11)最终得到:

该公式避免了传统方法中计算厄特弗斯改正的近似处理,也可用于计算重力水平分量。
3 算 例对于计算扰动重力垂向分量而言,传统方法与本文方法的主要差别在于垂向运动加速度的计算。传统方法是在当地坐标系下由- 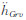 +δgE计算得到,而本文方法是在惯性系中计算再转换到当地坐标系,即方程(12)中的垂向加速度分量
+δgE计算得到,而本文方法是在惯性系中计算再转换到当地坐标系,即方程(12)中的垂向加速度分量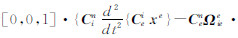
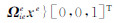 ,不需要计算厄特弗斯改正。为了验证本文方法的可行性,利用文献[21]中的部分航线进行了测试,航线为南北向飞行,高度约11 km,航速约为140 m/s,航空重力测量系统分别利用GPS接收机和L&R海空重力仪进行定位和重力测量。
,不需要计算厄特弗斯改正。为了验证本文方法的可行性,利用文献[21]中的部分航线进行了测试,航线为南北向飞行,高度约11 km,航速约为140 m/s,航空重力测量系统分别利用GPS接收机和L&R海空重力仪进行定位和重力测量。
图 2是利用Harlan公式进行厄特弗斯改正得到的运动加速度垂向分量,图 3是本文方法计算的相应结果。可以看出,两种方法得到结果基本一致,说明本文方法的结果是可靠的。图 4给出了两个结果的差值及统计数据,本文方法的结果能量有很微小的减少(标准偏差稍小),差值的标准差为74 μGal,这个差别主要是由于经典方法中的一些近似做法造成的。据Li(2013)的计算,Harlan公式忽略的地球扁率高阶项影响为几个μGal[17],这说明不考虑垂线偏差可能是造成两者差别的主要原因。图 4表明差值表现为零均值的高频特性,因此很容易利用低通滤波削弱或消除。表 1列出了3条航线两种方法结果的原始差值和利用不同截断频率滤波(1/20 s、1/30 s、1/60 s)后差值的统计信息,括号内为标准偏差,括号外为平均值。可以看出,利用截断频率为1/60 s的低通滤波器基本可以消除这种高频噪声,括号内为标准偏差,括号外为平均值。

|
| 图 2 由经典方法计算的运动加速度垂向分量 Fig. 2 Vertical Component of Kinematic Acceleration Computed by the Classical Method along the Flight |

|
| 图 3 由本文方法计算的运动加速度垂向分量 Fig. 3 Vertical Component of Kinematic Acceleration Computed by the Modified Method along the Flight |
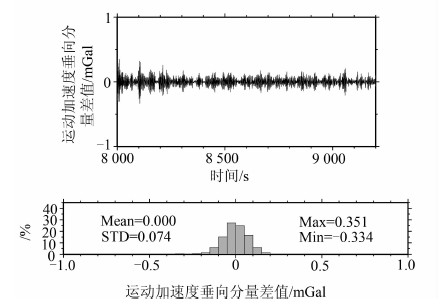
|
| 图 4 两种方法计算的运动加速度垂向分量差值 Fig. 4 Differences of Vertical Component Kinematic Acceleration Between the Classical Method and the Modified Method along the Flight |
| /mGal | ||||||
| 差值 | 航线A | 航线B | 航线C | |||
| 往测 | 返测 | 往测 | 返测 | 往测 | 返测 | |
| 原始值 |
-0.000 (0.138) |
0.000 (0.074) |
-0.000 (0.053) |
0.000 (0.069) |
-0.000 (0.054) |
-0.000 (0.058) |
 |
-0.000 (0.001) |
0.000 (0.001) |
-0.000 (0.002) |
0.000 (0.001) |
-0.000 (0.001) |
-0.000 (0.001) |
 |
-0.000 (0.000) |
0.000 (0.000) |
-0.000 (0.001) |
0.000 (0.000) |
-0.000 (0.001) |
-0.000 (0.001) |
 |
-0.000 (0.000) |
0.000 (0.000) |
-0.000 (0.000) |
0.000 (0.000) |
-0.000 (0.000) |
-0.000 (0.000) |
与经典方法相比,本文方法除了在计算扰动重力垂向分量时具有理论优势外,还提供了计算扰动重力水平分量的公式。为衡量计算结果的精度,可利用EGM2008模型[19]作为参考,计算出航线高度上的扰动重力模型值与本文计算结果进行比较,去除偏差和趋势项后的精度列于表 2。表 2中括号内为标准偏差,括号外为平均值。可以看出,本文方法得到的各条航线扰动重力垂向分量精度均优于2 mGal,水平分量精度优于10 mGal。本文计算结果采用的滤波器截断频率为1/60 s,对应分辨率约8.4 km。
| /mGal | ||||||
| 差值 | 航线A | 航线B | 航线C | |||
| 往测 | 返测 | 往测 | 返测 | 往测 | 返测 | |
| 北分量 | (5.386) | (0.892) | (1.738) | (2.129) | (9.119) | (6.996) |
| 东分量 | (2.135) | (2.498) | (8.359) | (8.069) | (7.594) | (0.857) |
| 垂向分量 |
-1.107 (0.705) |
-0.930 (0.712) |
-1.159 (0.876) |
-0.606 (1.054) |
0.327 (1.335) |
1.6922 (0.969) |
本文通过在准惯性坐标系下分离GPS测得的运动加速度与重力仪测得的比例值,建立了标量重力测量系统的一个新方程。改进方法提供了一个简洁严密的公式,避免了一些近似处理,在理论上对航空标量重力测量的经典方法进行了完善。在本文实例中,经典方法中的近似处理引起了亚mGal级的误差,这一误差经低通滤波后基本可以消除。但是在垂线偏差较大的地区,例如喜马拉雅山地区,经典方法会产生多大的误差有待于进一步研究。改进方法除了能够提供与经典方法相同精度的扰动重力垂向分量估值外,经过一些细致处理后还能得到扰动重力水平分量估值,精度比垂向分量稍差。
| [1] | Forsberg R,Olesen A V, Keller K, et al. Airborne Gravity and Geoid Surveys in the Arctic and Baltic Seas[C]. Proceedings of the International Symposium on Kinematic Systems in Geodesy, Geomatics and Navigation, Banff, Canada, 2001 |
| [2] | Olesen A V. Improved Airborne Scalar Gravimetry for Regional Gravity Filed Mapping and Geoid Determination[D]. Copenhagen:National Survey and Cadastre of Denmark, 2002 |
| [3] | Xia Zheren, Shi Pan, Sun Zhongmiao, et al. Chinese Airborne Gravimetry System CHAGS[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3):216-220(夏哲仁,石磐,孙中苗,等. 航空重力测量系统CHAGS[J]. 测绘学报,2004,33(3):216-220) |
| [4] | Hwang C W, Shiao Y S, Shih H C, et al. Geodetic and Geophysical Results from a Taiwan Airborne Gravity Survey:Data Reduction and Accuracy Assessment[J]. J Geophy Res, 2007, doi:10.1029/2005JB004220 |
| [5] | Sun Zhongmiao, Xia Zheren, Wang Xingtao. Determining Accuracy of Local Geoid Determined from Airborne Gravity Data[J]. Geomatics and Information Science of Wuhan University, 2007, 32(8):692-695(孙中苗,夏哲仁,王兴涛. 利用航空重力确定局部大地水准面的精度分析[J]. 武汉大学学报·信息科学版,2007,32(8):692-695) |
| [6] | Shi Pan, Sun Zhongmiao, Xiao Yun. Calculation and Spectra Analysis of Horizontal Acceleration Corrections(HACC) for Airborne Gravimetry[J]. Geomatics and Information Science of Wuhan University, 2001, 26(6):549-554(石磐,孙中苗,肖云. 航空重力测量中水平加速度改正的计算与频域分析[J]. 武汉大学学报·信息科学版,2001,26(6):549-554) |
| [7] | Xiao Yun, Xia Zheren. Determination of Moving-base Acceleration in Airborne Gravimetry[J]. Chinese Journal of Geophysics, 2003,46(1):62-67(肖云,夏哲仁. 航空重力测量中载体运动加速度的确定[J]. 地球物理学报,2003,46(1):62-67) |
| [8] | Liang Xinghui, Liu Lintao, Yu Shengjie. The Application of B-spline Least Squares in Determining Moving-base Acceleration for Airborne Vector Gravimetry[J]. Geomatics and Information Science of Wuhan University, 2009, 34(8):979-982(梁星辉,柳林涛,于胜杰. 利用B样条确定航空重力载体加速度的方法研究[J]. 武汉大学学报·信息科学版,2009, 34(8):979-982) |
| [9] | Sun Zhongmiao, Xia Zheren, Li Yingchun. Cross-coupling Correction for Lacoste & Romberg Airborne Gravimeter[J]. Geomatics and Information Science of Wuhan University, 2006, 31(10):883-886(孙中苗,夏哲仁,李迎春. Lacoste & Romberg航空重力仪的交叉耦合改正[J]. 武汉大学学报·信息科学版,2006, 31(10):883-886) |
| [10] | Thompson L G D, Lacoste L J B. Arial Gravity Measurements[J]. Journal of Geophysical Research, 1960,65(1):305-322 |
| [11] | Harlan R B. Eotvos Correction for Airborne Gravimetry[J]. Journal of Geophysical Research, 1968, 73(14):4675-4679 |
| [12] | Sun Zhongmiao. Calculation and Error Analysis of Eötvös Corrections for Airborne Gravimetry[J]. Journal of the PLA Institute of Surveying and Mapping, 1999,16(1):5-9(孙中苗. 航空重力测量中厄特弗斯改正的计算与误差分析[J]. 解放军测绘学院学报,1999,16(1):5-9) |
| [13] | Wall R E. Airborne Gravimetry Errors Associated with Geoidal Undulations[J]. Journal of Geophysical Research, 1971, 76(29):7293-7295 |
| [14] | Ouyang Yongzhong. On Key Technologies of Data Processing for Air-sea Gravity Surveys[D]. Wuhan:Wuhan University, 2013(欧阳永忠. 海空重力测量数据处理关键技术研究[D]. 武汉:武汉大学, 2013) |
| [15] | Brozena J M, Peters M F. An Airborne Gravity Study of Eastern North Carolina[J]. Geophysics, 1988, 53(2):245-253 |
| [16] | Li X. An Exact Formula for the Tilt Correction in Scalar Airborne Gravimetry[J]. Journal of Applied Geodesy, 2011, 5(2):81-85 |
| [17] | Li X.Examination of Two Major Approximations Used in the Scalar Airborne Gravimetric System-a Case Study Based on the LCR System[J]. Journal of Geodetic Science, 2013, 3(1):32-39 |
| [18] | Jekeli C. Inertial Navigation Systems with Geodetic Applications[M]. Berlin:Walter de Gruyter, 2000 |
| [19] | Pavlis N K, Holmes S A, Kenyon S C, et al. EGM2008:An Overview of Its Development and Evaluation[C]. IAG Int. Symp. GGEO, Chania, Crete, Greece, 2008 |
| [20] | Li X, Jekeli C. Ground-vehicle INS/GPS Gravimetry[J]. Geophysics, 2008, 73(2):Ⅰ1-Ⅰ10 |
| [21] | Li X.Strapdown INS/DGPS Airborne Gravimetry Tests in the Gulf of Mexico[J]. J Geod, 2011, 85(9):597-605 |
 2016, Vol. 41
2016, Vol. 41


