文章信息
- 徐武平, 邱峰, 徐爱萍
- XU Wuping, QIU Feng, XU Aiping
- 空间数据插值的自动化方法研究
- Automatic Method of Kriging Interpolation of Spatial Data
- 武汉大学学报·信息科学版, 2016, 41(4): 498-502
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 498-502
- http://dx.doi.org/10.13203/j.whugis20140131
-
文章历史
- 收稿日期: 2014-10-13

随机空间领域采样点的数量总是有限的,在数据建模中未采用点的值往往需要基于随机函数进行插值或预测,预测方法最好无偏差。克里金插值是常用的最好线性无偏差预测器[1],与其他的预测器相比,方差误差最小。克里金插值以变异函数理论和结构分析为基础,变异函数拟合模型的误差大小直接影响克里金插值的误差大小,要得到理想的插值结果,应选择拟合误差最小的变异函数模型。变异函数用来表示随机变量之间的相似性,当两随机变量距离较小时,它们是相似的,反之,则变异值较大。基本空间变异函数和空间克里金估值模型理论已经比较成熟,出现了ArcGIS、Geoda等地统计应用软件和基于ArcObjects的二次开发工具包,开发人员可以将其空间统计功能嵌入到已有的应用软件中。但这些空间分析统计类库中对变异函数的拟合和克里金的插值需由人工干预,且需要应用人员有一定的理论基础。文献[2, 3]中采用反复人工拟合变异函数的方法,得到视觉效果较好的拟合结果,但拟合过程复杂,对应用人员要求较高。由于变异函数的拟合结果是克里金插值的基础,而人工拟合明显不便于空间克里金插值的自动化,模型与拟合参数的选择也没有科学计算的依据.
本文基于R语言实现。R语言作为一种统计分析软件,集统计分析与图形显示于一体,完全免费、代码开源,其中的自动插值包[4]在本文中得到了很好的应用。本文首先研究如何读入需要拟合和插值的空间数据,然后研究空间变异函数的自动拟合,目的在于规范建模的步骤,提高建模的自动化程度,为自动克里金插值提供保障,最后基于变异函数自动拟合来实现自动克里金插值和自动交叉验证。拟将本文方法应用于国家重大专项“三峡库区水环境风险评估与预警”项目中,对数据建模所需的气象样本数据进行自动和准确的可靠性插值。
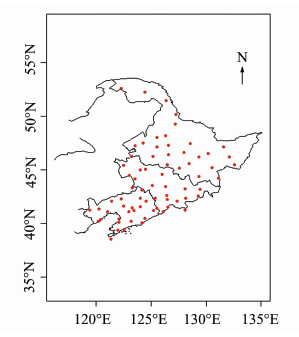
1 样本数据与待插值点的导入本文实验数据源于中国气象科学数据共享服务网的中国地面气候资料日数据集,包括中国752个地面气象观测站及自动站1951~2010年的数据集。数据集中了平均气温、平均最高气温、平均最低气温、平均相对湿度、最小湿度、降水量、平均气压,以及台站号、经纬度等信息。选取数据集中2009年6月6日东三省(黑龙江省、吉林省、辽宁省)的72个站点为采样点,范围为东经118°53′~135°05′,北纬38°43′~53°33′,图 1为站点分布图。
|
| 图 1 实验数据集和站点分布 Fig. 1 Dataset and Station Distribution Used in Experiment |
样点数据导入的代码如下:
fn1<-tk_choose.files(multi=FALSE,"*.xls")
channel<-odbcConnectExcel(fn1)
{table_name<-sqlTables(channel)$TABLE_NAME}
sqlstr<-paste(paste("select * from ",table_ name,sep="["),"",sep="]")
dataset<-sqlQuery(channel,sqlstr)
odbcClose(channel)
input_data<-as.data.frame(cbind(x= dataset [x坐标列],y= dataset [y坐标列],z= dataset [数据列]))
插值点的底图选用了东三省的植被图像坐标,如图 2所示。导入植被图像的代码如下:

|
| 图 2 插值点分布图 Fig. 2 Distribution of Interpolation Points |
data.grid <- read.csv(choose.files(),row.names = 1)
gridded(data.grid) = ~ x+y
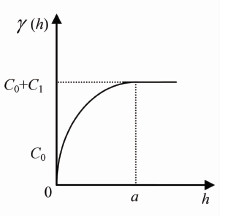
2 自动变异函数拟合变异函数值随着空间间隔的增加而单调增加,典型的变异函数曲线如图 3所示。在变异函数γ(h)中有a、C0和C0+C1[1]三个参数。其中,a被称为变程,它是变异函数值达到基台值时对应的h值,反映空间相关数据之间的最大距离;C0被称为块金值,是h为0时所对应的变异函数值;C1+C0被称为基台值,是数据间距离h大于a时的变异函数值,C1则被称为偏基台值,变异函数中一般用到的是偏基台值。
|
| 图 3 变异函数曲线 Fig. 3 Curve of Variogram |
随着地质统计学理论的发展,对变异函数的自动拟合出现了加权多项式回归法和线性规划法等多种方法。加权多项式回归拟合法以数据对的数目为权进行拟合,来计算实验变异函数不同滞后距h的数据对数目对样本变异函数计算结果的可靠性影响。该方法有可能因拟合参数值不符合模型要求而失败[4, 5]。
变异函数有一些常用、有效并通过实验验证的模型[1]。例如,球形模型(Sph)、指数模型(Exp)、高斯模型(Gau)、幂函数变异函数模型、对数模型、孔穴效应模型(Ste和 Mat)等。寻找合适变异函数模型的传统方法是使参数模型与样本变异函数相符合。这些模型中,应用较为广泛的是指数模型,球形模型,高斯模型,孔穴效应模型或这些模型的组合。拟合样本变异函数时,首先选定一个合适的模型(如“Sph”、“Exp”、“Gau”、 “Ste”、“Mat”),然后给定合适的初始偏基台值(Psill)、变程(range)和可能的块金值(nugget),按模型计算变异函数值,最后计算样本变异函数和模型变异函数的平均方差误差,误差越小则拟合效果越佳。
自动变异函数拟合根据科学的计算来选择变异函数模型和参数初始值。其基本思路如下[6]。
1) 计算数据框的对角线长;
2) 计算距离点对及各点对样本变异函数值;
3) 初始的块金值取样本变异函数的最小值;初始的变程取数据框的最大对角线长的三分之一;初始的基台值取样本变异函数最大值和样本变异函数最小值的平均值;
4) 分别对model = c("Sph","Exp","Gau","Ste","Mat")进行拟合,对"Ste"和"Mat"模型引入Kappa = c(0.05,seq(0.2,2,0.1),5,10)序列进行平滑处理,返回每个模型的拟合变程(fit_range),拟合基台值(fit_sill)和拟合块金值(fit_nugget)参数以及最小二乘法误差序列(SSerr_list);
5) 检测有无奇异的模型参数,若有,则去掉奇异模型及其参数。为了确保预测值与非负预测方差相关,所有观测点与任何可能的预测点之间的半变异函数值矩阵必须是正定的,非正定性的奇异模型须排除;
6) 按误差从小到大排序模型及其参数,取误差最小的模型及其最小误差作为拟合结果,返回最佳的空间变异函数模型及其偏基台值、变程、块金值和最小二乘法误差。最小二乘法使得变异函数模型拟合的结果与样本变异函数值之间误差的平方和最小。
在R语言中,变异函数自动拟合并封装成一个函数[4],调用方法为variogram = autofitVariogram(湿度~1,input_data)。其中input_data为样点数据,通过“auto_mode<- variogram$var_model”语句来获取自动拟合的模型,最后通过plot(variogram,xlab = "空间间隔(h)",ylab = "变异函数值(Variogram)")语句来绘制拟合图。
图 4是“湿度”数据的变异函数自动拟合结果,返回的最佳变异函数模型是“Ste”,psill值为82.741 27、range值为5.548 031、nugget值为38.610 94,平滑次数Kappa为10次,拟合的最小二乘法误差是169.9,拟合曲线很平滑。

|
| 图 4 变异函数自动拟合结果 Fig. 4 Automatic Fitting Result of Variogram |
克里金方法有简单克里金、普通克里金、协克里金和泛克里金等多种,普通克里金预测公式为:
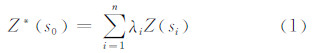
式中,Z*(s0)是空间点s0处插值的值;Z(si)是在空间点si(i=0,…,n)的采样值;λi是Z(si)的残差权重;n是预测过程中的样本个数;权重λi可以通过矩阵[1]由式 (2)计算得到:

式中,λij=λ(si-sj)是点si和sj之差的变异函数;μ是拉格朗日乘数;权重和拉格朗日乘数能通过R语言函数计算矩阵得到,然后通过式(1)计算出预测值Z*(s0)。
自动克里金插值将变异函数自动拟合嵌入其中,不需要用户一步步选择参数和模型进行拟合,变异函数自动拟合的结果直接为克里金权重矩阵的计算提供模型。调用方法如下:
Ordinary_kriging_result = autoKrige(湿度~1,input_data,data.grid)
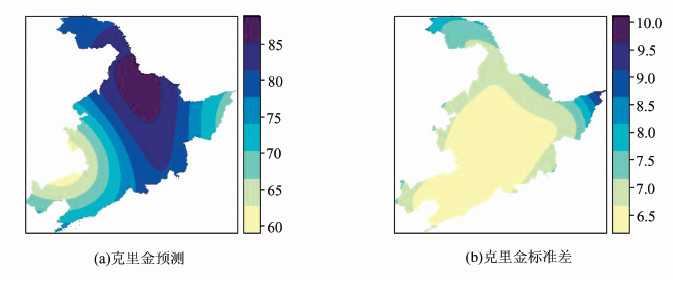
插值点选用了东三省的植被数据,该区域共有1 731 582个插值点,自动插值函数的参数formula、input_data、model、kappa、start_vals和fix_values参数同自动拟合函数,除此之外增加data_grid为插值点坐标,data_variogram为自动变异函数拟合的数据及其坐标。用绘图函数“plot(Ordinary_kriging_result)”得到如图 5所示的自动克里金插值的结果。图 5(a)是对东三省样点数据进行区域化自动克里金插值的结果,图 5(b)是对应的均方差误差,因此,实际误差范围大部份在2.55左右,但具体的误差还需要采用交叉验证来分析。
|
| 图 5 自动克里金插值结果 Fig. 5 Result of Automatic Kriging Interpolation |
传统的交叉验证一般将观测值暂时去除,然后通过其他观察值Z(x1)、…、 Z(xn)和变异函数模型来预测Z(xi)值,最后将预测值放回原始数据中,重复以上过程直到对所有观测点估值完成;接下来比较观测的实际值和估计值来诊断模型和参数。该方法需要一一预测观测值,对大规模的数据交叉验证速度较慢。本文在自动变异函数拟合基础上将数据集分为用于建模的集合和用于验证的集合。建模的集合用于变异函数自动建模,并在要验证的数据位置上进行自动克里金插值,然后将验证观测值与它们的预测值相比较。如果比较结果好,则交叉验证标准残差和标准化残差都很小,交叉验证标准残差为观测值与预测值之差。标准化残差(zscore)由式(3)计算[7]:

式中,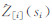 是对si的交叉验证预测值;σ[i](si)是相应的克里金方差。与标准残差相比,zscore考虑了克里金方差,如果变异函数模型是正确的,zscore应该有接近0的均值。自动交叉验证函数中的参数基本与自动克里金插值函数相同,只是增加了nfold=n,称其为n折交叉验证,即用于建模的数目为n个随机观测值,其余的观测值用于验证。自动交叉验证的调用方法如下:
是对si的交叉验证预测值;σ[i](si)是相应的克里金方差。与标准残差相比,zscore考虑了克里金方差,如果变异函数模型是正确的,zscore应该有接近0的均值。自动交叉验证函数中的参数基本与自动克里金插值函数相同,只是增加了nfold=n,称其为n折交叉验证,即用于建模的数目为n个随机观测值,其余的观测值用于验证。自动交叉验证的调用方法如下:
Auto_cv = autoKrige.cv(湿度~1,input_data,model = auto_mode[2, 1],nfold = 10)
cv_output<- Auto_cv $krige.cv_output
其中,auto_mode是在自动拟合中获得的模型,cv_output是自动交叉验证的输出,cv_output数据框中的列名称如图 6所示。

|
| 图 6 cv_output数据框的列名称 Fig. 6 Column Name of “cv_output” Dataset |
图 6中coordinates是数据的坐标,var1.pred是交叉验证的预测值,var1.var是交叉验证的误差值,observed是交叉验证前的观测值;residual是交叉验证残差,zscore是交叉验证标准化残差。使用一些绘图函数可得到图 7所示的误差分析图。图 7(a)是观测值(实线)与预测值(虚线)的折线图,其基本重合;图 7(b)中实线是标准残差,虚线是标准化残差(zscore),其基本接近0,由此可见本文所研究的自动克里金插值方法是可行的。

|
| 图 7 交叉验证标准残差和标准化残差 Fig. 7 Standard Residual and Standardizing Residual of Automatic Cross Validation |
本文在变异函数自动拟合原理的基础上,采用自动拟合方法来获取拟合模型,并将该模型应用于自动克里金插值以及自动交叉验证。通过实验分析了自动克里金插值的结果和误差(本文仅给出了“湿度”数据的实验结果)。研究结果表明,变异函数的自动拟合可得到最佳的模型和参数,该模型和参数为自动克里金插值和自动交叉验证的重要基础。变异函数自动拟合和自动克里金插值的实现对扩展国产GIS 的地质统计分析功能,开发具有较高自动化程度的地质统计软件包或应用于实时监控系统建模过程中的样本数据自动化插值具有很好的实际应用价值。至于在常用的应用软件开发环境C++或C#下如何嵌入R语言函数可参考文献[8]。
| [1] | Zhang Renduo.The Theory and Application of Space Variogram[M]. Beijing:Science Press,2005(张仁铎.空间变异理论及应用[M].北京:科学出版社,2005) |
| [2] | Li Sha, Shu Hong, Xu Zhengquan. Interpolation of Temperature Based on Spatial-temporal Kriging[J]. Geomatics and Information Science of Wuhan University, 2012, 37(2):237-241(李莎,舒红,徐正全.利用时空Kriging进行气温插值研究[J].武汉大学学报·信息科学版, 2012, 37(2):237-241) |
| [3] | Xu Aiping, Sheng Wenshun, Shu Hong. Interpolation and Validation Based on Spatiotemporal Product-sum Model[J]. Geomatics and Information Science of Wuhan University, 2012, 37(7):766-769(徐爱萍,圣文顺,舒红.时空积和模型的数据插值与交叉验证[J].武汉大学学报·信息科学版,2012, 37(7):766-769) |
| [4] | R-Prgect.org. CRAN-Package Automap[OL]. http://cran.r-project.org/web/packages/automap/index.html |
| [5] | Li Shaohua, Lu Wentao. Automatic Fit of the Variogram[C]. Third International Conference on Information and Computing, Wuxi, China, 2010 |
| [6] | Pesquer L, Cortés A, Pons X. Parallel Ordinary Kriging Interpolation Incorporating Automatic Variogram Fitting[J]. Computers & Geosciences, 2011,37(1):464-473 |
| [7] | Xu Aiping, Shu Hong. Applied Spatial Data Analysis with R[M]. Beijing:Tsinghua University Press,2013(徐爱萍,舒红,译.空间数据分析与R语言实践[M].北京:清华大学出版社,2013) |
| [8] | Zheng Xingwen, Hu Hongda, Xu Jiaqi, et al. The Mixed Programming Component of Ordinary Kriging[J]. Urban Geotechnical Investigation & Surveying, 2013,6:139-142(郑兴文,胡泓达,许家琦,等. Kriging插值组件的混合编程实现[J]. 城市勘测, 2013,6:139-142) |
 2016, Vol. 41
2016, Vol. 41



