文章信息
- 黄伟明, 杨建宇, 陈彦清, 张毅, 张睿
- HUANG Weiming, YANG Jianyu, CHEN Yanqing, ZHANG Yi, ZHANG Rui
- 基于扇形筛选法的矢量数据压缩方法
- Method of Vector Data Compression Based on Sector Screening
- 武汉大学学报·信息科学版, 2016, 41(4): 487-491
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 487-491
- http://dx.doi.org/10.13203/j.whugis20140225
-
文章历史
- 收稿日期: 2014-07-30

2. 国土资源部农用地质量与监控重点实验室, 北京, 100035;
3. 中国地质大学(北京)地球物理与信息技术学院, 北京, 100083
2. Key Laboratory for Agriculture Land Quality, Monitoring and Control of the Ministry of Land and Resources, Beijing 100035, China;
3. School of Geophysics and Information Technology, China University of Geosciences, Beijing 100083, China
随着地理数据获取能力的不断增强,网络地理信息系统(Web Geographic Information System,WebGIS)所需处理、传输的数据量也越来越大。数据量的增大使得地理空间信息和知识的获取更加容易,但在某些具体应用中,庞大的数据量不仅占用过多的存储空间,也降低了WebGIS软硬件系统的效率。因此,有必要根据具体的应用需求对地理数据进行压缩。
GIS数据主要分为矢量数据与栅格数据两种数据结构。其中,矢量数据因拓扑关系易于表达、结构比较紧凑、冗余度低等优点应用更为广泛。但相对栅格数据压缩而言,矢量数据压缩算法还不够成熟,这是因为矢量数据具有复杂性与格式多样性,导致对其压缩有相当的难度[1]。
从现有的研究成果看,矢量数据压缩按照压缩后能否完全重建原数据可以分为有损压缩和无损压缩[1]两种。无损压缩主要是利用编码的方法(如Huffman编码、算数编码等)对原数据进行压缩,在需要的时候再利用特定的解码方法重建原数据[2]。有损压缩则在压缩后无法完全重建原数据。它可以针对不同的应用需求产生不同精度的矢量数据。无损压缩一般不考虑地理数据具有的特性,不如有损压缩应用广泛。
Douglas等[3]提出了著名的Douglas-Peucker算法(以下称为“DP算法”)[3, 4]。Shekhar[5]等利用将坐标表示为增量再聚类的方式压缩矢量数据。Yang[2, 6]等提出了一种能在一定程度上保持拓扑一致性的基于簇模型的矢量地图压缩方法。朱海军等[7]提出利用离散余弦变换来压缩矢量数据的方法,能够实现较大的压缩比,且能将失真控制在一定限值内。马伯宁等[8]提出了一种具有误差修正的线矢量数据小波变换,实现了用小波变换进行矢量数据压缩时过大误差的修正。黄培之[9]在DP算法的基础上提出了一种具有预测功能的矢量数据压缩方法,在相同的误差限值下相较DP算法能够获得更大的压缩比,但效率不高。
本文针对文献[9]提出的具有预测功能的曲线矢量数据压缩方法(以下将其中的“顾及精度的最长距离边端点的直接预测算法”简称为“预测算法”)展开探讨,首先从理论上改进该算法,以提高其寻找预测区域内最长边端点时的效率;其次对预测区域大小的选取初步探讨;最后进行对改进算法与DP算法进行对比实验。
1 预测算法原理具有预测功能的曲线矢量数据压缩方法是文献[9]提出的一种对顾及精度的较长距离边寻求算法的改进算法,即顾及精度的最长距离边端点的预测算法,在相同化简阈值下可以得到更大的压缩比。
预测算法的基本思路是[9]:对于某一给定的曲线和确定的化简阈值来说,从起始点出发,按照曲线走向依次检测后续点,如果起始点与待检测点组成的连线与二者之间所有中间点的垂距dn均小于阈值,则继续检测下一个点;否则,该点的前一个点为所确定的较长距离边(以下将其简称为“较长边”)端点的第一个候选点。当确定了最长边端点的第一个候选点后,对它之后的m个点(m由曲线具体情况而定)继续用前面提到的较长边端点的选取方法检测,这m个点即为预测算法中的“预测区域”。若检测到预测区域中某点,起始点与该点之间连线与所有中间点的垂距dn均小于阈值,同时对该点的下一个点进行检测时不能符合上述条件,则该点为最长边端点的又一个候选点。之后再以新的最长边端点候选点的后续曲线选定新的预测区域,用上述方法继续检测,直至预测区域内的所有点都不是最长边端点候选点的又一个取值,则此时已获得的最后一个最长边端点的候选点成为最长边端点。即起始点与最长边端点之间的点都被移除了。之后再以最长边端点为下一条边的起始点,进行后续曲线的压缩。
图 1是一个典型的利用预测算法化简曲线的例子。对于以Po为起点的曲线和一个给定的大小适当的阈值来说,首先寻找较长边端点。由Po开始,按照曲线走向进行检测,当检测的点为Pj之前的点时,Po与该点连线到所有中间点的垂距dn都小于阈值,当Pj作为待检测点时,检测到Pk到PoPj的垂距dk大于阈值,因此Pj的上一个点Pj-1就成为最长边端点的第一个候选点,再对Pj-1之后的点进行探索,发现当探索到Pj+2时,PoPj+2与所有中间点的垂距dn都小于阈值,则Pj+2满足最长边端点候选点的条件,同时它又是曲线的最后一个端点,则这条曲线被化简为PoPj+2。

|
| 图 1 预测算法化简曲线示意图 Fig. 1 Sketch Map of Simplifying Curves by Prediction Algorithm |
在上述算法中,曲线最终被化简为直线,实现了较大的压缩比。在同样的化简阈值下,预测算法相对于DP算法来说能够实现更大的压缩比。但这种算法在执行时,每当需要验证某点是否为新的最长边端点候选点时,需要求算较多中间点到起始点与该点相连直线的垂距,运算量较大。黄培之[9]曾提出一种比较两个夹角正切值大小的方法来提高计算效率,但对于走向不固定的曲线,或者对于算法中所涉及的两个夹角正切值有正有负甚至不存在的情况来说,它会忽略一些潜在的最长边端点的候选点,造成压缩比降低。
关于预测区域大小的选取问题,目前还没有一个全自动的方式。对于某一特定的要素类和化简阈值来说,一定有一个最小的预测区域大小可以使得用此算法压缩后的压缩比达到最大。且对于同一个要素类来说,阈值越大则在预测区域内出现新的最长边端点候选点的可能性越大。所以在一般情况下,为了达到更大的压缩比,当阈值增大时应当选取更大的预测区域。在本文实验中,预测区域的大小将选取可以使压缩比达到最大的最小值。
2 基于扇形筛选法的矢量数据压缩方法针对原预测算法效率不高的问题,本文提出一种扇形筛选法以减少在预测区域内寻找最长边端点时求算距离的次数。
2.1 方法原理 根据§1中描述,每一个最长边端点候选点(整条曲线最后一个点除外)的下一个点一定不符合成为最长边端点的条件,即起始点与其中间至少有一个点到它们之间连线的垂距dn大于阈值。对于最长边端点候选点的下一个点来说,在实际计算过程中,当找到了某一中间点到相对应直线的垂距dn大于阈值后,也就不需要再计算其余中间点与直线的距离了,此时该点已不满足成为最长边端点候选点的条件了。利用与相对应直线垂距大于阈值的第一个中间点,可以降低算法在预测区域中的运算量,提升算法的效率。具体来说,当找到一个新的最长边端点的候选点,将其下一个点与起始点的连线记作l时,存在某一点Pk与l的垂距dk大于阈值。以Pk为圆心,阈值为半径作圆,以起始点Po为起点作两条射线与这个圆相切。这样整个二维平面也就被分成了两个无穷大的扇形区域,此时再检测预测区域内的后续点,若后续点与圆心Pk在同一个区域内,则该点有可能成为最长边端点的又一个候选点,反之则不可能。预测方法在探索预测区域内的点时可以首先利用这个方法提前筛选,剔除一些不可能成为该最长边的端点的点,以提高算法效率。
图 2是上述改进算法的示意图。以Po为起点的曲线,检测到Pj时发现Pk到直线PoPj的垂距dk大于阈值h,则以Pk为圆心,以h为半径作圆,从Po出发作射线与该圆相切,将整个二维平面分成了两个无穷大的扇形区域。检测后续点时,将Pk所在的扇形区域作为指定区域,判断点是否在指定区域内。例如点Pj+1不在指定区域内,则认为它不可能成为最长边端点的候选点,而它的下一个点Pj+2在指定区域内,则认为它有可能成为最长边端点候选点的又一个取值,再连接PoPj+2计算中间点与这条直线的距离以验证其是否满足成为最长边端点候选点的条件。上述过程中,不需要计算PoPj+1与其中间点的垂距,提升了算法的效率。
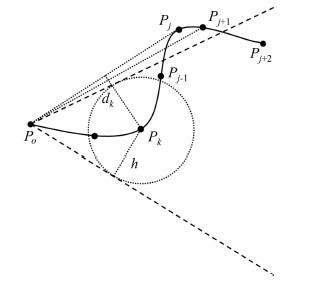
|
| 图 2 算法改进示意图 Fig. 2 Sketch Map of the Algorithm Improvement |
下面对这个方法的原理进行简单说明。首先,Po点必然在以Pk为圆心、以h为半径的圆外,因为如果Po在圆内或圆上时,则Pk到它与任何一点的连线的垂距都不可能大于阈值h。若有一点在指定区域之外,以Pj+1为例,根据“圆心到圆外直线距离必大于半径”可知,作Pk到PoPj+1的垂距一定大于h。这也就说明了为什么指定扇形区域之外的点一定不可能成为最长边端点的候选点。
2.2 实现策略上述改进方法在具体编程实现过程中,可以利用计算斜率的方式来减少求算切线解析式所用的时间。斜率的求解实质上是一个一元二次方程的求解问题,设:
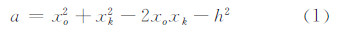
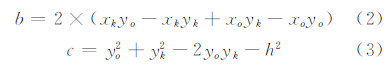
式中,(xo,yo)、(xk,yk)为图 2中Po和Pk的纵坐标;h为化简阈值。
求得两条切线的斜率为:
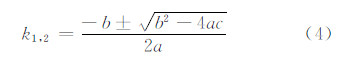
式中,k1,2代表两条切线的斜率。
计算出两条切线的斜率后,整个二维平面也就被分成了4个无穷大的扇形区域(此处求得的斜率为直线的斜率,因此被分成了4个区域),下一个最长边端点的候选点应与圆心Pk在同一个区域内。需要说明的是,实际运算中有可能出现切线斜率不存在的状况,但在计算过程中可以判断正无穷与负无穷的出现,这对于实际运算效果并没有什么影响。
3 实验与分析为了验证上述算法的可靠性及改进效果,笔者在Windows 8平台上,使用C#实现了预测算法、本文算法及DP算法。使用数据为北京市通州区矢量等高线图的一部分,要素类中共有42 855个端点,占用700 KB的存储空间。笔者选取多个不同的化简阈值,用预测算法、本文算法及DP算法对上述数据进行了化简(其中预测区间大小选取的是前文提到过的能在此算法下实现最大压缩比的最小值),将实验过程中各个算法化简所需时间记录下来以进行对比,如表 1所示。
| /ms | |||||
| 算法 | 阈值 /m | ||||
| 1 | 2 | 5 | 10 | 20 | |
| 预测算法 | 39.40 | 44.30 | 68.42 | 90.80 | 122.82 |
| 本文算法 | 25.76 | 29.45 | 45.90 | 62.41 | 86.70 |
| DP算法 | 78.64 | 71.84 | 64.05 | 57.49 | 51.66 |
由表 1可以看出,本文算法与预测算法相比,效率大约提升了30%~40%。这主要是因为本文算法在预测区域内寻找最长边端点时求算距离的次数变少了,取而代之的是较为简单的斜率计算。
接下来将在压缩比和压缩后误差两个方面对比本文算法和DP算法(预测算法与本文算法的压缩比和压缩后误差是完全一样的)。此处误差指的是被移除点位移的均方根,计算公式如下:
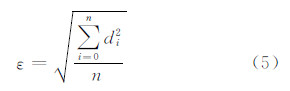
式中,ε为压缩误差;di为第i个压缩点到压缩后曲线的误差距离;n为压缩后被移除的点的个数。
不同算法在不同阈值下产生的压缩比和压缩误差见表 2。
| 阈值/m | 1 | 2 | 5 | 10 | 20 | |
| 压缩比/% | 本文算法 | 53.01 | 68.53 | 81.05 | 87.08 | 91.07 |
| DP算法 | 47.88 | 63.83 | 78.00 | 85.04 | 89.68 | |
| 误差/m | 本文算法 | 0.74 | 1.24 | 2.95 | 5.72 | 11.27 |
| DP算法 | 0.68 | 1.02 | 2.14 | 3.94 | 7.26 |
表 2中的实验结果可以证实文献[9]中的结论,在相同误差限值下,预测算法能够取得更大的压缩比;但在压缩比提高的同时也增加了压缩后产生的误差,特别是在阈值较大、压缩比较高的压缩结果中,误差明显变大。由此可见,本文算法在这一方面相对来说更适合阈值较小的压缩任务。
结合表 1和表 2的实验结果可以看出,当阈值较小,压缩比在80%以下时,本文算法在效率上相对DP算法有较大优势。这是因为,DP算法中阈值越大,需要求算距离的次数越少,计算效率越高;本文算法中,阈值越大则需要求算距离的次数越多,计算效率越低。这说明本文算法在压缩效率方面也比较适合阈值相对较小,压缩比要求不高的压缩任务;而DP算法则较适合压缩比要求较高的任务。
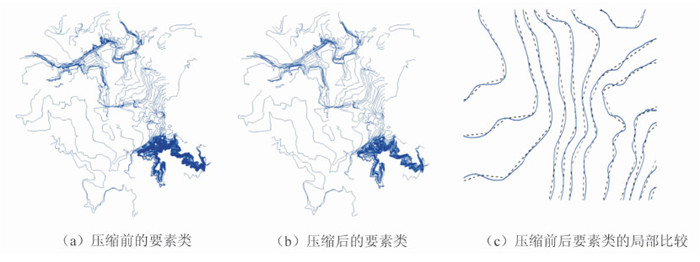
图 3表示的是该地区等高线矢量数据利用本文算法压缩前后的效果(阈值为20 m,预测区域大小为18个点,局部比较图中实线和虚线分别代表压缩前和压缩后的等高线)。图 3中等高线压缩比达到91.07%,其形态结构特征也得到了较好的保持。
|
| 图 3 压缩前后的要素类的全局和局部比较 Fig. 3 Visual Comparison of Original Map and Compressed Map |
本文针对预测算法的效率低下问题提出了一种较为高效的矢量数据有损压缩方法,能够根据不同的应用需求获取不同精度的数据。由实验结果可以得出,本文算法对预测算法的效率有了较大的提升,在相同化简阈值下具有比DP算法更高的压缩比,可以较好地保持线状地理要素的形态,且其压缩结果不受曲线走向影响。
相对于DP算法,在化简阈值较小时,本文算法在计算效率方面存在优势。是否能将本文算法与DP算法结合利用,当指定阈值较小时利用本文算法进行压缩;当指定阈值较大时利用DP算法进行压缩,以提高WebGIS中处理和传输不同精度数据的总体效率,值得进一步研究。同时,化简阈值与预测区间大小如何确定也有待于进一步研究。
| [1] | Yang Jianyu, Yang Chongjun, Ming Dongping, et al. Review on Vector Data Compression and Simplification of WebGIS[J]. Computer Engineering and Applications, 2005, 40(32):36-38(杨建宇,杨崇俊,明冬萍,等. WebGIS系统中矢量数据的压缩与化简方法综述[J].计算机工程与应用.2005,40(32):36-38) |
| [2] | Yang B, Purves R S, Weibel R. Variable-resolution Compression of Vector Data[J]. Geoinformatica, 2008, 12(3):357-376 |
| [3] | Douglas D H, Peucker T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J]. The Canadian Cartographer, 1973, 10(2):112-122 |
| [4] | Cao Zhenzhou, Li Manchun,Cheng Liang, et al. Progressive Transmission of Vector Curve Data over Internet[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4):475-479(操震洲,李满春,程亮,等.矢量曲线数据的网络渐进传输[J].武汉大学学报·信息科学版,2013,38(4):475-479) |
| [5] | Shekhar S, Huang Y, Djugash J, et al. Vector Map Compression:a Clustering Approach[C].The 10th ACM International Symposium on Advances in Geographic Information Systems, McLean, Virginia, USA, 2002 |
| [6] | Yang B, Purves R, Weibel R. Efficient Transmission of Vector Data over the Internet[J]. International Journal of Geographical Information Science, 2007, 21(2):215-237 |
| [7] | Zhu Haijun, Wu Huayi, Li Deren. DCT-Based GIS Vector Data Compression[J]. Geomatics and Information Science of Wuhan University, 2008, 32(12):1123-1126(朱海军,吴华意,李德仁.基于DCT变换的GIS矢量数据压缩技术研究[J].武汉大学学报·信息科学版, 2008,32(12):1123-1126) |
| [8] | Ma Boning, Leng Zhiguang, Tang Xiaoan, et al. Wavelet Transform with Error Correction for Line Vector Data[J]. Journal of Computer-Aided Design & Computer Graphics, 2011, 23(11):1825-1829(马伯宁,冷志光,汤晓安,等.具有误差修正的线矢量数据小波变换[J]. 计算机辅助设计与图形学学报,2011,23(11):1825-1829) |
| [9] | Huang Peizhi. Vector Data Compression with Prediction Function[J]. Acta Geodaetica et Cartographica Sinica, 1995, 24(4):316-320(黄培之.具有预测功能的曲线矢量数据压缩方法[J].测绘学报,1995,24(4):316-320) |
 2016, Vol. 41
2016, Vol. 41



