
文章信息
- 郑肇葆, 郑宏
- ZHENG Zhaobao, ZHENG Hong
- 带有确定度的模糊图像分类
- Fuzzy Image Classification with a Certain Degree
- 武汉大学学报·信息科学版, 2016, 41(4): 482-486
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 482-486
- http://dx.doi.org/10.13203/j.whugis20150712
-
文章历史
- 收稿日期: 2015-11-30

2. 武汉大学电子信息学院, 湖北 武汉, 430072;
3. 武汉大学深圳研究院, 广东 深圳, 518000
2. School of Electronic Information, Wuhan University, Wuhan 430072, China;
3. Shenzhen Institute, Wuhan University, Shenzhen 518000, China
文献[1]曾应用图像关联度作了图像模糊分类的研究,研究结果表明该方法具有较好的图像分类效果。该方法的不足是不能直接应用图像关联度确定待识别图像的类别,需要采用逐次趋近的办法才能完成图像类别的识别,这样的识别过程比较耗时。为此,本文引用确定度的概念[2, 3, 4]作为关联度的权,由加权的关联度确定待识别图像的类别,这是本文图像模糊分类的核心。
1 带有确定度的图像模糊识别方法本文的图像模糊识别方法是在图像模糊识别的关联度方法基础上进行的,本文首先简述一下图像关联度的概念,之后介绍带有确定度的图像模糊识别的原理和方法。
1.1 图像的关联度[1]假定有3组图像,用组1、2、3表示,每组图像的像幅数为n1、n2、n3,每组图像的纹理特征均值分别为Fmean1、Fmean2、Fmean3。计算第一组中每幅图像纹理特征相对3组纹理特征均值之差d1(i1,1)、d1(i1,2)、d1(i1,3):
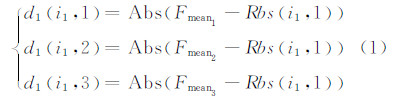
式中,Abs为取绝对值的符号;Rbs(i1,1)表示组1中第i1幅图像的特征值;类似地有相应于组2、组3中每幅图像纹理特征Rbs(i2,2)和Rbs(i3,3)相对组1、2、3特征均值之差的绝对值:
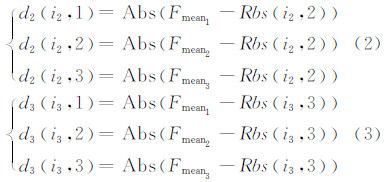
组1中每幅图像相对三个组的关联度为r1(i1,1)、r1(i1,2)、r1(i1,3),计算如下:
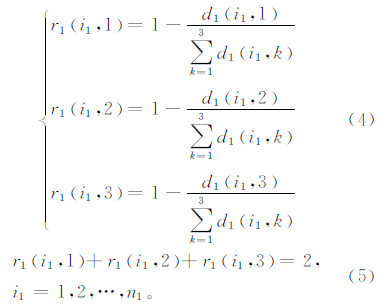
式(5)表示关联度的一个特征,即一幅图像相对三个组图像的关联度之和等于2。类似式(4),可以求得组2、组3中每幅图像相对三个组的关联度r2(i2,1)、r2(i2,2)、r2(i2,3)和r3(i3,1)、r3(i3,2)、r3(i3,3),具体表达式可参见文献[1]。
1.2 确定度计算[2, 3, 4]§1.1说明了3个组中图像的特征与3个组的关联程度,接下来研究确定度对基于关联度图像模糊分类的影响。
假定组1中一幅图像相对3个组图像的确定度分别为CF1(i1,1)、CF1(i1,2)、CF1(i1,3),相应表达式如下:
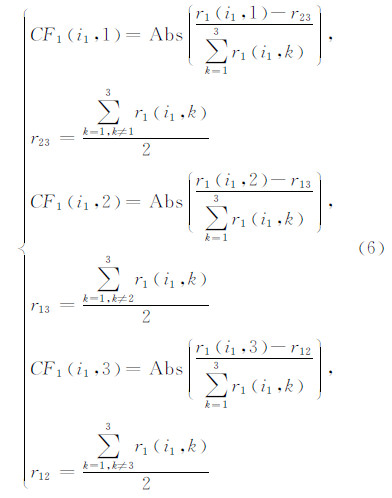
式中,r1(i1,1)、r1(i1,2)、r1(i1,3)表示组1中第i1幅图像相对1,2,3组图像的关联度。
组2中一幅图像相对3个组图像的确定度分别为:
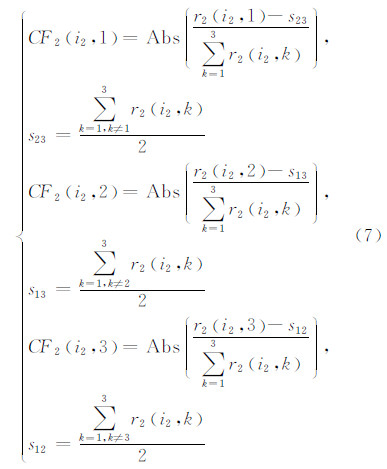
组3中图像相对3个组的确定度分别为:
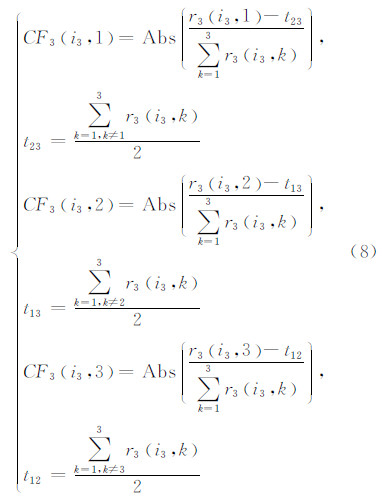
假定有3种不同类别的图像,按类别被分为3组,组1有n1幅,组2、组3分别有n2、n3幅。若一幅图像不知道它是3个类别中哪一类,可以按以下方法确定。
(1) 待识别图像的第一种判据:先将待识别图像放在组1中,计算该幅图像在组2中带有确定度的关联度CFR1(i1,1)、CFR1(i1,2)和CFR1(i1,3):
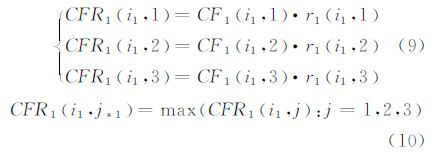
式(10)中,j*1表示求得最大CFR1(i1,j)的组别号。
(2)将待识别图像放在组2中,计算该幅图像在组2中带有确定度的关联度CFR2(i2,1)、CFR2(i2,2)和CFR2(i2,3):
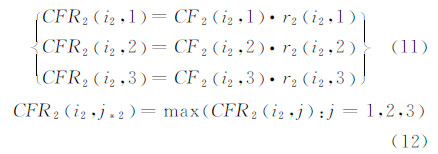
(3) 将待识别图像放在组3中,得到类似的带有确定度的关联度:

如果由式(10)、(12)、(14)求得的j*1、j*2、 j*3都相等,即

则表明待识别图像属第一组图像类别。如果3个j*数值不同,则该待识别图像类别不能确定。
2 利用带有确定度的关联度进行待分类图像模糊识别的第二种判据假定3个类别图像的像片数分别为n1、n2、n3,分别求出待分类图像安排在组1、2、3的最后时,各组带有确定度的关联度的均值为Rmean1、Rmean2和Rmean3,用待分类图像所在组别的带有确定度的关联度CFR1(n1+1,1)、CFR2(n2+1,2)、CFR3(n3+1,3),计算出与三个组别的均值差,即
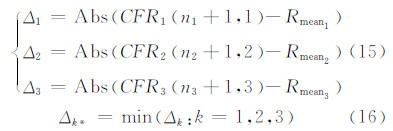
式(16)中,k*表示Δk中具有最小值的下标,k*的数值即为待分类图像的类别组号。式(15)和式(16)即为本文使用图像分类的第二种判据。
3 试验与分析为了验证本文图像分类方法的正确性,使用航空摄影像片做图像分类试验,其中灌木52幅、居民地23幅、河流35幅、山地20幅、水田13幅,分别由3种不同地物组成一个组合,共7个组合。下面列举部分实验数据说明使用本文图像分类方法的效果。
(1) 在灌木、河流、山地组合中进行灌木图像的识别。一幅待识别的灌木图像,先后放在灌木组(k=1)的最后、河流组(k=2)的最后、山地组(k=3)的最后,进行3次试验,试验结果见表 1。表 1中第2行数据为待识别图像,在灌木组最后,求得该图像与灌木、河流、山地的带有确定度的关联度,其中与灌木的关联度最大为6.38×10-2。表 1中第4行数据为待识别图像,放在河流组最后,求得该图像分别与3组图像的带有确定度的关联度,其中与灌木的关联度最大为6.57×10-2。同样地,当待识别图像放在第3组(山地)图像最后,求得该图像分别与3组图像的带有确定度的关联度(见第6行),其中与灌木的关联度最大为6.64×10-2。按本文待识别图像第一判据,表 1中的第2、4、6行的灌木这一列的数据最大,因此待识别图像为灌木。识别结果与已知的待识别图像的属性一致。
| 灌木k=1 | 河流k=2 | 山地k=3 | |
| CFR152,k | 6.38×10-2 | 5.90×10-2 | 3.86×10-2 |
| CFR152,1-Rmean1=4.39×10-2 | |||
| CFR235,k | 6.57×10-2 | 6.37×10-2 | 3.91×10-2 |
| CFR235,2-Rmean2=2.40×10-2 | |||
| CFR320,k | 6.64×10-2 | 5.85×10-2 | 4.58×10-2 |
| CFR320,3-Rmean3=1.69×10-2 | |||
(2) 在灌木、河流、水田组合中进行灌木图像识别。与前一个实验相似,待识别的灌木图像先后分别放在该组合的3组图像中,进行3次试验,试验结果列在表 2中。
| 灌木k=1 | 河流k=2 | 山地k=3 | |
| CFR152,k | 6.13×10-2 | 6.91×10-2 | 9.25×10-2 |
| CFR152,1-Rmean1=4.91×10-2 | |||
| CFR235,k | 6.42×10-2 | 1.17×10-2 | 9.25×10-2 |
| CFR235,2-Rmean2=7.32×10-2 | |||
| CFR313,k | 6.47×10-2 | 6.33×10-2 | 10.16×10-2 |
| CFR313,3-Rmean3=4.94×10-2 | |||
从表 2第2行CFR1(52,k)的3个数据中,位于灌木这一列的数据不是最大,在第4、6行中相应的3个数据中,位于灌木这一列的相应数据也不是最大,按本文待识别图像的第一判据无法判定待识别图像为灌木。但表 2中第3、5、7行的数据分别由式(15)计算得出,其中最小值为4.91×10-2,Δk*=Δ1,即待识别图像为灌木。这就是用第二种判据识别的结果。
(3) 在灌木、居民地、水田组合中识别居民地。与前面实验相似,待识别的居民地图像先后分别放在该组合的3组图像中,进行3次试验,试验结果列在表 3中。
| 灌木k=1 | 河流k=2 | 山地k=3 | |
| CFR152,k | 5.25×10-2 | 6.84×10-2 | 7.27×10-3 |
| CFR152,1-Fmean1=7.28×10-2 | |||
| CFR223,k | 5.52×10-2 | 7.45×10-2 | 7.25×10-3 |
| CFR223,2-Fmean2=5.56×10-2 | |||
| CFR313,k | 5.71×10-2 | 6.63×10-2 | 1.72×10-2 |
| CFR313,3-Fmean3=6.58×10-2 | |||
从表 3的第2、4、6行数据中可以看出,每行中属于居民地这一列的数值最大,由第一判据可知,待识别图像为居民地。我们再注意表 3中第3、5、7行数据中,第5行的CFR2(23,2)-mean2=5.56×10-2 数值最小,由图像识别的第二判据知道,待识别图像为居民地。表 3中试验结果告诉我们,待识别图像有时同时满足两个判据的要求,实际工作中只要满足一个判据就可以确定待识别图像的类别,无须两个判据同时满足。图像识别过程中,两个判据条件同时使用,提高了识别的效率。
(4) 从试验中我们认识到,合理的图像组合可以得到较好的识别效果。但是怎样才能得到较好的图像组合,这是值得研究的问题。
(5) 带有确定度的关联度图像模糊分类结果与其它方法的比较。从表 4中对比结果可见,本文提出的图像模糊分类方法是可行的、有效的。
(6) 要说明的是,带有确定度的关联度直接用于图像的模糊识别,不像直接使用关联度的图像模糊识别,需要多次迭代完成。
| [1] | Zheng Zhaobao, Pan Li, Zheng Hong. Application of Image Correlation Degree to Image Fuzzy Classification[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5):574-577(郑肇葆,潘励,郑宏. 应用图像关联度的图像模糊分类[J]. 武汉大学学报·信息科学版,2015,40(5):574-577) |
| [2] | Ishibuchi H, Nakashima T. Effect of Rule Weights in Fuzzy Rule-Based Classification Systems[J]. IEEE Transactions on Fuzzy Systems,2001,9(4):506-515 |
| [3] | Ishibuchi H,Nozaki K, Tanaka H. Distributed Representation of Fuzzy Rules and Its Application to Pattern Classification[J]. Fuzzy Sets and Systems,1992,52:21-32 |
| [4] | Nozaki K, Ishibuchi H,Tanaka H. Adaptive Fuzzy Rule-based Classification Systems[J]. IEEE Transactions on Fuzzy Systems,1996,52(1):21-32 |
| [5] | Zheng Zhaobao,Zheng Hong. Genetic Algorithm for Producing Texture "TUNED" Masks[J]. Pattern Recognition and Artificial Intelligence, 2001, 14(1):119-122(郑肇葆,郑宏. 产生纹理"Tuned"模板的遗传算法[J]. 模式识别与人工智能,2001,14(1):119-122) |
| [6] | Zheng Zhaobao, Pan Li, Yu Xin. Bayesian Networks for Producing Texture "Tuned" Masks[J]. Geomatics and Information Science of Wuhan University, 2006,31(4):304-307(郑肇葆,潘励,虞欣. 产生"Tuned"模板的Bayesian Networks方法[J]. 武汉大学学报·信息科学版,2006,31(4):304-307) |
| [7] | Zheng Zhaobao. Honey-bee Mating Optimization Algorithm for Producing Better "Tuned" Masks[J]. Geomatics and Information Science of Wuhan University, 2009,34(4):387-399(郑肇葆. 产生最佳"Tuned"模板的蜜蜂交配算法[J]. 武汉大学学报·信息科学版,2009,34(4):387-390) |
 2016, Vol. 41
2016, Vol. 41



