文章信息
- 白生祥, 郑春弟, 张森
- BAI Shengxiang, ZHENG Chundi, ZHANG Sen
- 利用加权联合协方差矩阵拟合进行干涉相位估计
- Interferometric Phase Estimation Based on Weighted Joint Covariance Matrix Fitting
- 武汉大学学报·信息科学版, 2016, 41(4): 475-481
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 475-481
- http://dx.doi.org/10.13203/j.whugis20140224
-
文章历史
- 收稿日期: 2015-03-17

2. 海军工程大学电子工程学院, 湖北 武汉, 430033
2. Electronic College of Engineering, Naval University of Engineering, Wuhan 430033, China
干涉合成孔径成像技术作为一种新兴的高分辨率、高精度三维成像技术,是目前遥感探测、地形测绘领域的研究热点[1]。干涉合成孔径信号处理的三个关键步骤是图像配准、干涉相位滤波和相位展开[2]。在干涉处理过程中,这三个步骤依次级联,前一步骤存在的误差,会依次累积并传递到下一步中。一个较小的配准误差就可能导致错误的相位展开结果,因此,对配准误差稳健的干涉相位估计方法进行研究具有十分重要的意义。
近年来,干涉合成孔径雷达(interferometric synthetic aperture radar,InSAR)技术中提及的许多相位滤波方法,如圆周期均值滤波、圆周期中值滤波、自适应滤波算法[3, 4]等,都要求图像精确配准,否则难以准确恢复真实干涉相位。文献[5]提出了一种基于联合像素模型的子空间投影方法,能够在配准误差不超过一个分辨单元的条件下准确地估计干涉相位,为干涉信号处理开辟了新的途径。之后,许多文献进行了深入研究[6, 7, 8, 9, 10, 11, 12],拓展了其应用。采用联合子空间投影估计方法估计干涉相位时,存在信号子空间向噪声子空间扩散的问题,困扰着子空间方法性能的提升。文献[6]提出一种COMET-EXIP方法,由于该方法不需要对联合协方差矩阵进行特征分解,避免了信号子空间扩散的影响;但COMET-EXIP方法在估计干涉相位过程中存在相位模糊的问题,对于有限样本的情形,其解模糊的前提条件不能恒成立,从而导致相位估计结果可能出现模糊,影响到算法的稳健性。本文基于加权联合协方差矩阵拟合的思想[12, 13],提出一种单基线干涉相位估计方法。该方法能够摆脱子空间扩散和相位模糊的影响,获得更加稳健的干涉相位估计性能。
1 统计模型本文简要介绍像素数据的统计模型,详情参见文献[5]。假定InSAR复图像对已精确配准,且已去平地相位,对同一像素i(对应于同一地面单元),两个传感器(卫星天线)阵列接收的复数据矢量s(i)可表示为:
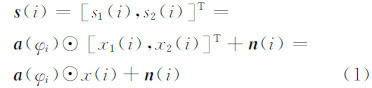
式中,a(φi)=[1,ejφi]T为空间导向矢量;s1和s2分别为传感器1和传感器2所对应的复图像数据;x(i)为像素i的复幅度矢量(即不同传感器接收的复散射矢量);n(i)为图像中的加性零均值高斯白噪声;φi为真实地形的干涉相位,这也是要估计的参数;⊙表示Hadamard积。式(1)中,s(i)称为空间数据矢量,可以描述为联合零均值复周期高斯随机矢量,其对应的联合协方差矩阵Cs(i)为:
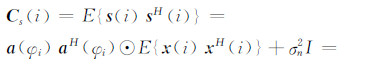
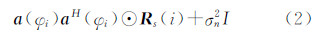
式中,Rs(i)为像素i的相关矩阵,定义为:
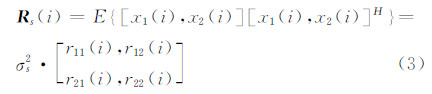
式中,rmn(i)(0≤rmn(i)≤1,m=1,2,n=1,2)为像素i在传感器m和n间的相关系数;I为2×2的单位阵;σs2为像素i的回波能量;σn2为噪声能量。
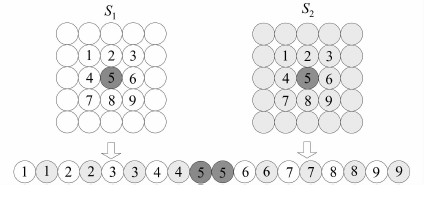
在实际情况中,两幅图像很难完全精确配准,当存在一定的配准误差时,基于单像素处理的干涉相位估计方法将失效。在这种背景下,文献[5]提出联合像素模型,它的基本思想是利用当前待估计像素及其相邻像素具有相同的统计特征这一重要特性,通过综合利用邻近像素对的相干信息,从统计估计的角度,使得干涉相位尽可能得到恢复。典型的联合像素模型构造中像素窗为(3×3,3×3),如图 1所示。此时,联合观测数据矢量为:
|
| 图 1 联合像素模型构造示意图 Fig. 1 Formulation of Joint Data Vector |
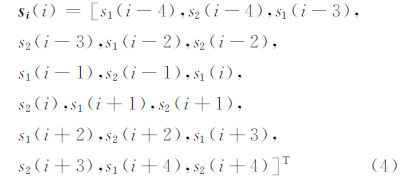
对应的联合协方差矩阵Csi(i)为:
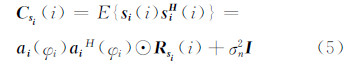
假设联合观测数据矢量si(i)的相邻像素所处的局部区域为平地,则有:
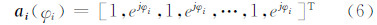
对子空间拟合的思想进行拓展,使得拟合的空间不仅仅是信号子空间或噪声子空间,而是一个与接收数据有关的矩阵。为了便于推导,首先从联合协方差矩阵的拟合开始,与COMET-EXIP方法类似,可构造如下的拟合关系:
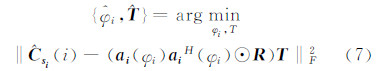
式中,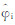 为估计的干涉相位;
为估计的干涉相位; 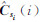 为样本联合协方差矩阵,假设其维数为M,则
为样本联合协方差矩阵,假设其维数为M,则 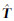 是一个M×M维的辅助参量矩阵;R的值由式(8)表示:
是一个M×M维的辅助参量矩阵;R的值由式(8)表示:
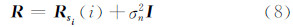
式(7)给出的拟合问题是一个二维可分离的最小二乘问题,固定φi就可以求出 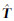 的最小二乘解:
的最小二乘解:
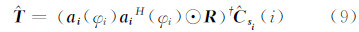
式中, 表示矩阵伪逆。对的求解涉及角度搜索问题和矩阵求逆运算,运算量巨大。为简化计算,选取一个对角矩阵作为的解取代的最小二乘解,即:
表示矩阵伪逆。对的求解涉及角度搜索问题和矩阵求逆运算,运算量巨大。为简化计算,选取一个对角矩阵作为的解取代的最小二乘解,即:
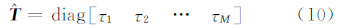
式中,τ1τ2…τM是M个复变量。将式(10)代入式(7),则联合矩阵协方差矩阵拟合可转化为式(11)所示的M个独立的列向量拟合问题:
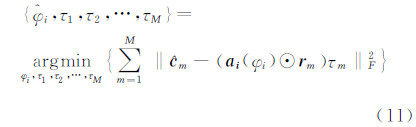
式中,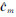 和rm分别表示
和rm分别表示  和R的第m列,实际中rm由abs(
和R的第m列,实际中rm由abs( 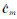 )予以近似。式(11)同样是一个可分离的最小二乘问题,τm的最小二乘解为:
)予以近似。式(11)同样是一个可分离的最小二乘问题,τm的最小二乘解为:
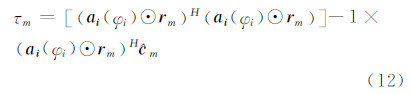
结合式(6)分析可知,式(12)中方括号内的项为一与φi无关的常数,因而运算量可大大降低。将式(12))代入式(11)可得到关于相位估值 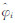 的解:
的解:
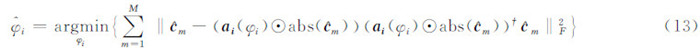
在各态历经的假设条件下,样本联合协方差矩阵 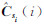 通过有限的独立同分布样本计算得到,但有限的样本必然导致估计误差。由于样本联合协方差矩阵
通过有限的独立同分布样本计算得到,但有限的样本必然导致估计误差。由于样本联合协方差矩阵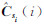 中第(m,n)个元素的估计误差与该元素对应的联合观测数据矢量si(i)中第m和n个像素间的相关系数近似成反比[12],因此,为降低估计误差的影响,一种更稳健的方法是对相关系数加权后的样本联合协方差矩阵进行拟合。设第(m,n)个元素对应的相关系数为|γmn|,整个相关系数矩阵为(|γmn|),则加权后的样本联合协方差矩阵可表示为:
中第(m,n)个元素的估计误差与该元素对应的联合观测数据矢量si(i)中第m和n个像素间的相关系数近似成反比[12],因此,为降低估计误差的影响,一种更稳健的方法是对相关系数加权后的样本联合协方差矩阵进行拟合。设第(m,n)个元素对应的相关系数为|γmn|,整个相关系数矩阵为(|γmn|),则加权后的样本联合协方差矩阵可表示为:

将式(14)代入式(7),仿照式(9)~式(13)的求解过程,得到 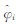 的解为:
的解为:
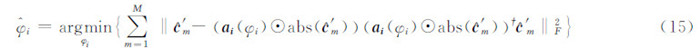
式中,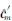 表示
表示 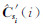 的第m列。式(15)可进一步表示为:
的第m列。式(15)可进一步表示为:
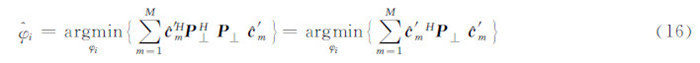
式中,
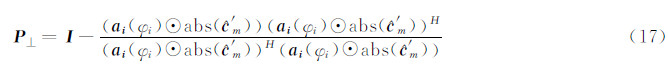
将式(17)代入式(16)并化简后得:
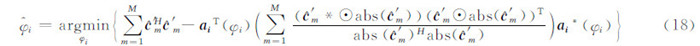
经过上面的一系列推导就完成了干涉相位的估计问题,但直接采用式(18)进行搜索计算量仍然十分巨大。基于此,提出一种快速计算方法,通过给出 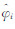 的闭式解形式避免干涉相位的搜索问题。
的闭式解形式避免干涉相位的搜索问题。
式(18)中 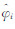 的求解问题等价于式(19)代价函数Jc求最大值的问题:
的求解问题等价于式(19)代价函数Jc求最大值的问题:
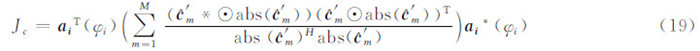
为了便于推导,令:
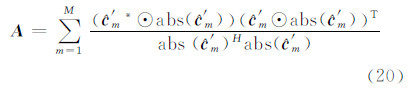
容易证明,矩阵A为M×M维的Hermitian矩阵,以2N表示偶数M,将A表示为2×2维的子矩阵组成的分块矩阵形式,则式(19)可写为:
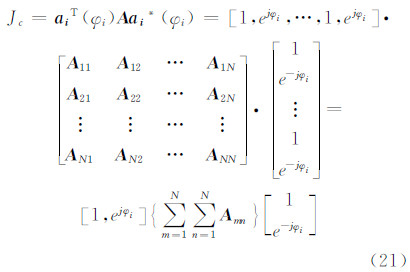
式中,Amn为A的子矩阵。令:

易知B2×2同样为Hermitian矩阵。令b21=|b21|ejμ(-π≤μ<π),则有:
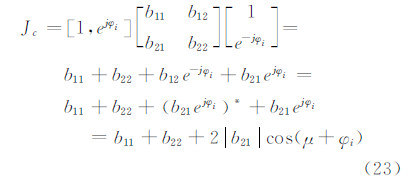
由式(23)可知,当μ+φi=2kπ(k为整数)即φi=2kπ-μ时,代价函数取得最大值。又因为φi为干涉相位,其取值范围为-π≤φi<π,所以其估计结果 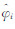 可表示为:
可表示为:
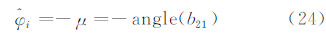
采用加权联合协方差矩阵拟合方法估计干涉相位可分以下4个步骤。
(1) 图像粗配准
利用传统的图像配准算法(如相关法)对SAR图像进行配准。只要图像配准误差不超过一个分辨单元即可,因此图像配准的复杂程度和运算量大大降低。
(2) 估计联合协方差矩阵
构造联合观测矢量si(i),计算相应的联合协方差矩阵Csi(i)。在满足各态历经性的条件下,可用样本协方差矩阵按式(25)进行估计:

式中,2L+1为获得的独立同分布的样本数。
(3) 估计加权相关系数矩阵
实际中,相关系数矩阵也是通过样本平均得到的。令sim(i)和sin(i)分别表示联合观测矢量si(i)中第m和n个样本,则相关系数|γmn|可用式(26)估算:
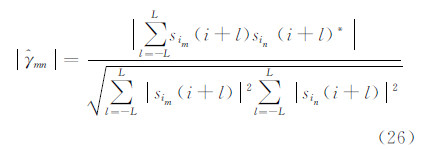
(4) 加权联合协方差矩阵拟合
利用式(18)构造参数为φi的拟合关系式,使代价函数达到最大值时,通过式(24)求出所对应的干涉相位 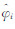 即为最优估计。
即为最优估计。
对合成孔径图像中的每个分辨单元按照上述4个步骤逐一操作,就能够精确地恢复实际的干涉相位。
4 处理性能验证为了验证加权联合协方差矩阵拟合方法的有效性,采用InSAR仿真数据和实测数据,对其与联合子空间投影方法以及COMET-EXIP方法进行比较。
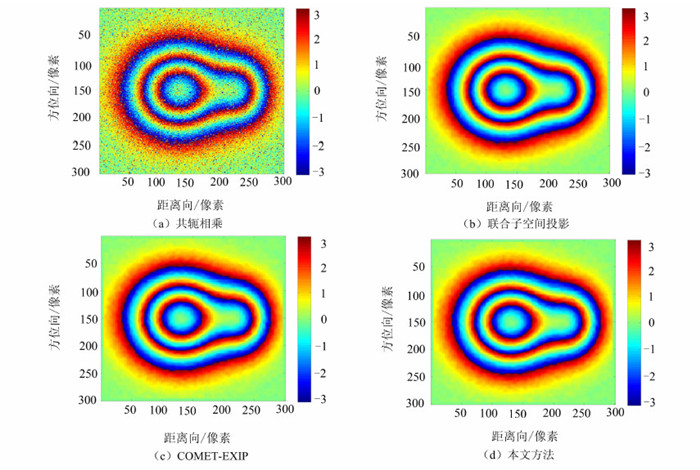
4.1 InSAR仿真数据采用文献[14]中提出的仿真方法生成回波信号,经合成孔径成像处理后,对图像进行相干处理得到干涉相位图。图 2为两幅合成孔径图像精确配准时不同方法的处理结果。从图 2可以看出,在精确配准条件下,各方法都能够正确估计出干涉相位。
|
| 图 2 精确配准时各相位估计方法处理结果 Fig. 2 Comparasion of Interferogram for Accurate Coregistration |
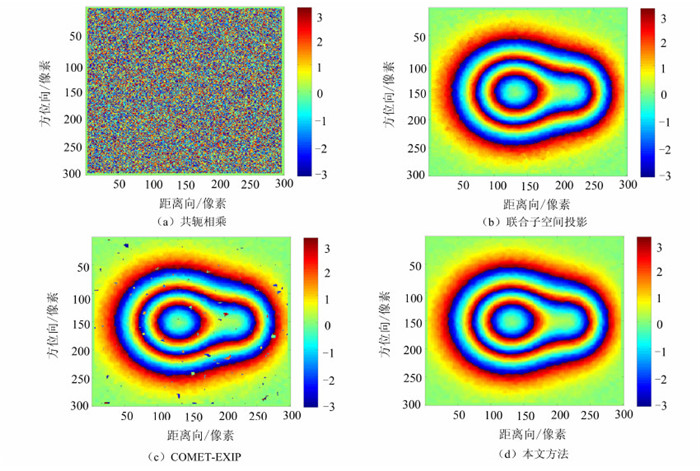
图 3为两幅图像存在1个像素配准误差时不同方法处理得到的干涉相位。从图 3中可知,此时联合子空间投影和加权联合协方差矩阵拟合方法可以较好地恢复干涉相位,其中加权联合协方差矩阵拟合方法条纹更清晰,性能更优;COMET-EXIP方法也基本能够恢复干涉相位,但却存在一些误差较大的离散点,这是由于COMET-EXIP方法在估计过程中出现相位模糊造成的,对于出现模糊的像素点,估计结果和真实值存在大小为π的偏差。
|
| 图 3 存在1个像素配准误差时不同方法的处理结果 Fig. 3 Comparasion of Interferogram for the Coregistration Error of 1 Pixel |
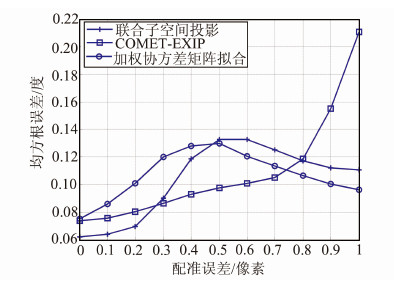
图 4为不同配准误差条件下,三种干涉相位估计方法所得结果的均方根误差变化情况。从图 4中可以看出,COMET-EXIP方法由于相位模糊的影响,在配准误差大于0.8后,相位估计误差明显增加;加权联合协方差矩阵拟合方法相比其它两种方法,对配准误差的变化适应性更好,在配准误差较大的情况下依然能够保持较好的相位估计性能。
|
| 图 4 均方根误差随配准误差的变化 Fig. 4 Standard Deviation Versus Coregistration Error |
采用合成孔径雷达X-SAR获取的一组意大利Enta火山口数据对各方法处理性能进行验证。该数据在大量文献中用于干涉信号处理方法的性能验证,具有很强的代表性。
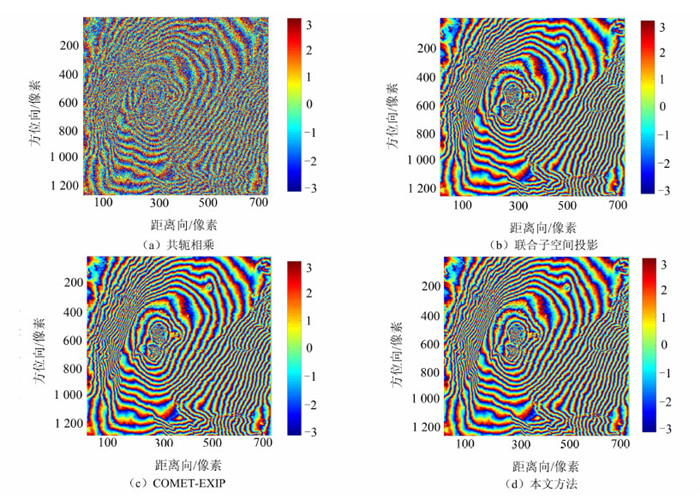
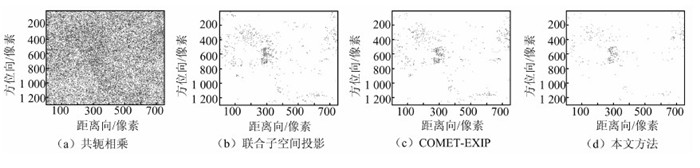
图 5展示了不同干涉相位估计方法的估计结果,其中图 5(a)为直接共轭相乘得到的干涉相位图,图 5(b)为联合子空间投影方法估计的干涉相位图,图 5(c)为COMET-EXIP方法估计的干涉相位图,图 5(d)为加权联合协方差矩阵拟合方法估计的干涉相位图。图 6为与图 5对应的残余点分布图。表 1给出了相应的残余点统计情况。无论从图 5的相位质量,图 6的残余点的分布情况还是残余点的数目来看,三种方法相比,加权联合协方差矩阵拟合方法均具有最优的处理效果。
|
| 图 5 各相位估计方法对Enta数据处理结果 Fig. 5 Interferograms for the Data of Enta |
| 估计方法 | 共轭相乘 | 联合子空间投影 | COMET-EXIP | 本文方法 |
| 残余点 | 179 151 | 8 250 | 6 778 | 3 755 |
|
| 图 6 不同估计方法处理结果的残余点分布图 Fig. 6 Residual Distribution of Different Interferometric Phase Estimating Methods |
本文提出一种基于加权联合协方差矩阵拟合的快速干涉相位估计方法,该方法能够充分利用联合观测数据矢量中的相干信息,通过对加权联合协方差矩阵进行拟合来实现干涉相位估计。该方法不需进行特征分解和子空间划分,因而可以避免子空间投影方法的信号子空间扩散难题,而且不存在类似COMET-EXIP方法的相位模糊问题,具有更好的配准误差适应能力。利用仿真数据和InSAR实际数据分析和比较了联合子空间投影、COMET-EXIP和加权联合协方差矩阵拟合方法的性能,结果表明,加权联合协方差矩阵拟合方法对配准误差更具稳健性,能够获得更优的干涉相位估计效果。
| [1] | Rosen P A,Hensley S,Joughin I R,et al.Synthetic Aperture Radar Interferometry[J].Proc. IEEE,2000,88(3):333-382 |
| [2] | Zhong Heping,Tang Jinsong,Zhang Sen,et al.A Fust Unwrapping Algorithm Based on Quantized Quality Map and Priority Queue[J].Geomatics and Information Science of Wuhan University,2011,36(3):342-345(钟何平,唐劲松,张森,等.利用量化质量图和优先队列的快速相位解缠算法[J].武汉大学学报·信息科学版,2011,36(3):342-345) |
| [3] | Yi Huiwei,Zhu Jianjun,Chen Jianqun,et al.An Improved Adaptive Algorithm for Filtering InSAR Interferogram in Complex Plane[J].Journal of Central South University(Science and Technology),2013,44(2):632-641(易辉伟,朱建军,陈建群,等.一种改进的InSAR干涉图复数空间自适应滤波[J].中南大学学报(自然科学版),2013,44(2):632-641) |
| [4] | Yu Xiaoxin,Yang Honglei,Peng Junhuan,et al.A Modified Goldstein Algorithm for InSAR Interferogram Filtering[J].Geomatics and Information Science of Wuhan University,2011,36(9):1051-1054(于晓歆,杨红磊,彭军还,等.一种改进的Goldstein InSAR干涉图滤波算法[J].武汉大学学报·信息科学版,2011,36(9):1051-1054) |
| [5] | Li Z,Bao Z,Li H.Image Autocoregistration and InSAR Interferogram Estimation Using Joint Subspace Projection[J].IEEE Transaction on Geoscience and Remote Sensing,2006,44(2):288-297 |
| [6] | Zhang Sen,Tang Jinsong,Chen Ming.Image Autocoregistration and Interferogram Estimation Using an Extended COMET-EXIP Method[J].IEEE Transactions on Geoscience and Remote Sensing,2010,44(2):288-297 |
| [7] | Li Hai,Wu Renbiao,Liao Guisheng.Estimation of Interferometric Phase for InSAR Based on Correlation Coefficient Weight Data Vector[J].Acta Electronica Sinica,2012,40(3):453-458(李海,吴仁彪,廖桂生.基于相关系数加权观测矢量的InSAR干涉相位估计方法[J].电子学报,2012,40(3):453-458) |
| [8] | Zhang Xiaoling,Chen Qin,Wei Shunjun.Estimation Method for Pol-InSAR Multi-Interferometric Phase Based on the MUSIC Method[J].Journal of University of Electronic Science and Technology of China,2011,40(5):652-657(张晓玲,陈钦,韦顺军.基于MUSIC算法的Pol-InSAR相位估计方法[J].电子科技大学学报,2011,40(5):652-657) |
| [9] | Liao Guisheng,Li Hai.Estimation Method for InSAR Interferometric Phase Based on Generalized Correlation Steering Vector[J].IEEE Trans. Aerospace and Electronic Systems,2010,46(3):1389-1403 |
| [10] | Zhang Sen,Xu Yanyi,Tang Jinsong.A Robust Estimation Method of Interferometric Phase Based on Weighted Subspace Fitting[C].The 2nd International Congress on Image and Signal Processing(CISP'09),Tianjin,2009 |
| [11] | Zhang Sen,Tang Jinsong,Zhu Sanwen.Image Autocoregistration and Interferogram Estimation Using Matrix Fitting[C].International Symposium on Computer Science and Computational Technology(ISCSCT 2008),Shanghai, 2009 |
| [12] | Liu N,Zhang L R,Liu X,et al. Multi-baseline InSAR Height Estimation Through Joint Covariance Matrix Fitting[J].IET Radar,Sonar and Navigation,2009,3(5):474-483 |
| [13] | Wang Yongliang,Chen Hui,Peng Yingning,et al.Methods and Algorithms of Spatial Spectrum Estimation[M].Beijing:Tsinghua University Press,2005(王永良,陈辉,彭应宁,等.空间谱估计理论与算法[M].北京:清华大学出版社,2005) |
| [14] | Chen M,Zhang S,Tang J S. An Interferometric Synthetic Aperture Sonar Raw Signal Simulation based on Points-Scatterer Model[C].International Joint Conference on Computational Sciences and Optimization,Sanya, 2009 |
 2016, Vol. 41
2016, Vol. 41


